高速公路隧道临近段车辆换道持续时间生存分析

陈政，温惠英

（华南理工大学，土木与交通学院，广州 510641）

0 引言

车道变换是交通安全领域的重要研究课题，车辆在车道变换期间，驾驶人需要对周围的交通运行状态进行实时分析，选择目标车道和最佳的换道时机，以期到达特定车道或获得更好的驾驶条件[1]。由于车道变换是一个多阶段的决策过程，驾驶人不仅需要关注其所处车道前后方车辆运行状态，还需要处理周边车辆的运行信息，这增加了驾驶人的工作量及心理压力，导致驾驶人决策失误率增加，存在较高的行车风险[2]。而随着换道阶段驾驶人所处交通环境复杂度的上升，驾驶人换道决策的失误率也越高[3]。

由于隧道特殊的管状结构，其内部与外部的行车环境存在较大差异。隧道内昏暗的行车环境以及驾驶人驾车通过隧道洞口时经历的照度明暗变化都会对行车安全产生不利影响[4]。因此，驾驶人在车辆进入隧道前会在交通条件允许的情况下，提前换入行车视野较好的车道，以此来降低隧道环境对行车安全产生的影响。从隧道路段交通事故的空间分布特征来看，临近隧道路段的事故率最高，并且事故类型以追尾和侧面碰撞为主，大多是由驾驶人的换道决策失误导致的[5]。因此，研究隧道临近段车辆换道特性对提升道路交通安全水平具有较强的现实意义。

换道持续时间作为研究车辆换道特性的关键指标，研究方向主要集中于换道持续时间特征和影响因素的作用机理方面[6]。Toledo 等[7]将换道过程定义为换道车辆横向位移单向连续变化的过程，并通过对Next Generation Simulation（NGSIM）数据进行分析，发现车辆在3～13 s完成换道。车辆换道行为决策受换道方式、车速、驾驶人心理-生理特性以及周边交通场景等多重因素影响[8]。Yang等[9]通过分析自然驾驶数据采集到的实际车辆换道数据，研究了不同等级道路和不同交通状态下的换道临界间隙与换道持续时间特性。李林波等[10]采用半参数的生存分析建模方法，研究不同种类影响因素对换道持续时间的影响。对于特定、复杂场景下的换道持续时间研究大都是通过模拟驾驶试验进行的，柳本民等[11]通过驾驶模拟器采集了高速公路冰雪低摩阻路面车辆的换道行为数据，通过生存分析方法对换道持续时间分布特征进行研究，定量分析了潜在因素对换道持续时间的影响。

以往研究方法假设不同驾驶人对影响因素的反应是相同的，忽略了不同驾驶人对换道风险感知水平的差异。同时，在车辆换道时间特征研究中广泛应用的生存分析半参数估计方法，其在建模时难以考虑驾驶人的异质性。此外，受数据采集技术的限制，对隧道临近路段这类特殊、复杂的交通场景，目前大多是通过模拟驾驶实验采集车辆换道数据，但模拟驾驶实验难以真实还原行车场景，给驾驶人以实际的行车体验，因此，在分析结果上还是存在一定的偏差。

因此，本文在既有研究基础上，通过自然驾驶试验采集高速公路隧道临近路段车辆换道数据，引入生存分析理论研究不同行车环境下隧道临近路段的车辆换道时间特征，并考虑不同驾驶人换道风险感知水平的异质性，构建随机参数加速失效时间模型，分析隧道临近段行车环境、车辆运行状态等因素对车辆换道持续时间的影响。本文方法可为改善高速公路隧道路段行车安全水平提供理论依据。

1 数据采集

本文定义隧道临近段为车辆从高速公路普通路段到隧道进口的过渡路段。依据隧道对车流和驾驶行为的影响范围，将隧道临近段划定为隧道进口至隧道进口前1.5 km 的区间[12]，图1 为高速公路隧道临近段示意图。为研究高速公路隧道临近段车辆换道持续时间特性，本文通过在多条高速公路隧道临近路段开展自然驾驶试验，采集试验车辆及周边车辆的换道数据。

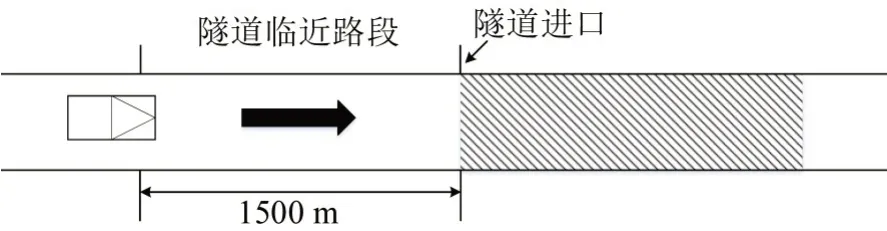
图1 高速公路隧道临近段示意图Fig.1 Schematic of adjacent section of freeway tunnel

1.1 试验地点

选择广东省韶关市京港澳高速公路上的乌坑坝隧道（1337 m）、石门坳隧道（1120 m）和媲双坳隧道（750 m）为试验隧道，3 条隧道皆为双向4 车道的分离式隧道，隧道内有照明，隧道外路段限速100 km·h-1，隧道内限速80 km·h-1。

1.2 试验驾驶人

试验共选取73名驾驶人，其中，48名男性驾驶人，25名女性驾驶人，平均驾龄均在3年以上，矫正视力均在0.8以上，无重大交通事故记录，对道路熟悉程度一般，使用同一车辆在3条试验隧道路段各进行4 次自然驾驶试验，共计开展876 次自然驾驶试验。

1.3 试验时间

自然驾驶试验于2020年3～9月进行，试验时间选在晴朗的白天。

1.4 试验车辆及试验仪器

试验车型选用小型轿车，实验仪器包括：毫米波雷达、GPS、三轴加速度计、行车记录仪，如图2所示。

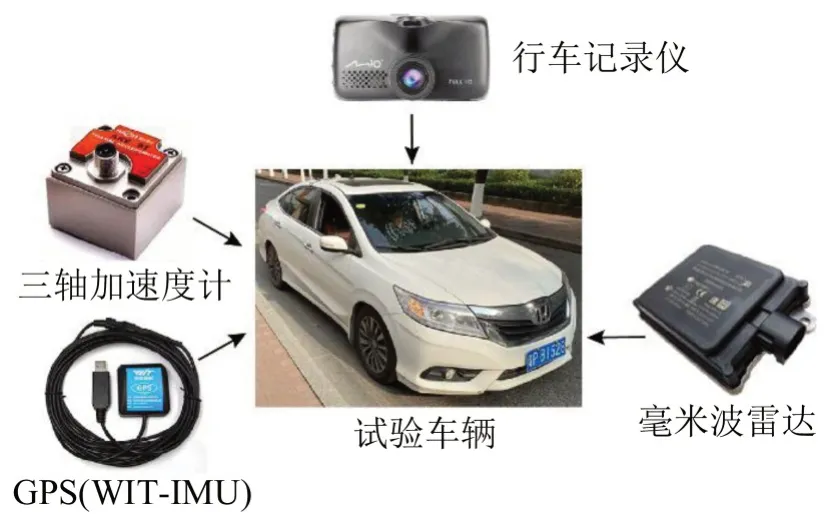
图2 自然驾驶试验仪器设备Fig.2 Naturalistic driving test apparatus

1.5 试验过程及数据描述

1.5.1 试验过程

本文数据采用实车行驶的实时数据采集方式，为保证采集隧道临近段车辆换道数据的真实性，试验过程中未要求试验车辆驾驶人进行主动换道操作，而是让其自主选择驾驶策略。在试验车中的成员使用仪器设备记录试验车辆的车速、横纵方向加速度、时间、位置、车道，以及周边车辆的相对位置、速度等数据，共得到876组实车试验数据。

车辆换道过程如图3所示，车辆从T0时刻开始换道，并于T2时刻驶入目标车道，完成换道过程。为获取准确的车辆换道信息，依据所采集的车辆位置与横向速度的变化情况，分别对换道行为和换道起止时刻进行识别，从而实现车辆换道轨迹数据的提取。

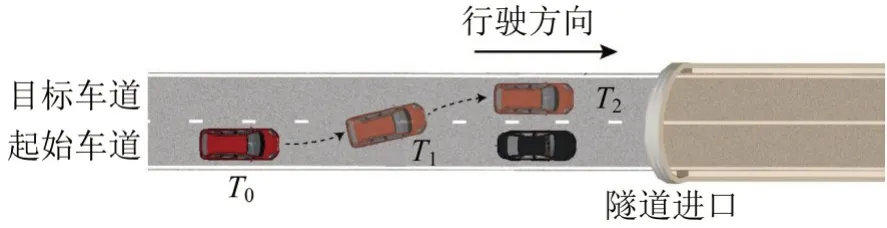
图3 车辆换道过程Fig.3 Lane change process

与城市道路相比，高速公路的车流密度相对较低，同时自然驾驶试验的车辆换道数据采集方法存在较强的随机性。对车辆换道数据识别和提取后，最终得到有效换道数据234条，换道数据统计情况如表1 所示。高速公路隧道临近段车辆换道时间平均值为5.55 s，中位数5.26 s，标准差为1.66 s，小于4 s 的比例为14.53%，约19.66%的数据大于7 s，约68.38%的数据分布在4～7 s范围内。

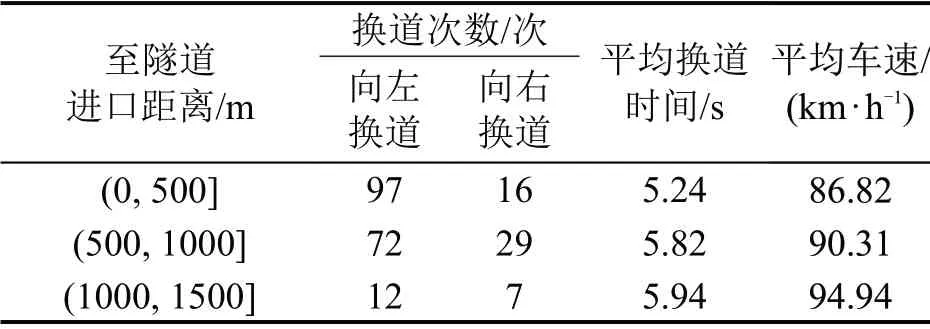
表1 换道数据统计Table 1 Statistics of lane changing behaviors

1.5.2 数据描述

高速公路隧道临近段车辆换道持续时间的影响因素主要考虑换道方向特性、与隧道的相对位置、换道车辆与周边车辆的相对运动状态、换道车辆自身的运行状态及目标车道行车环境的影响。其中，目标车道行车环境主要与车辆间的相对位置有关，即换道车辆开始换道时与目标车道的前车间隙和后车间隙，由于后随车间隙不受自身控制，故相对前车间隙是个更为重要的因素[13]。

本文从换道方向、至隧道进口的距离、换道起始跟驰距离、换道车辆速度、与起始车道前车的车速差、至目标车道前车距离等6个方面选取15项影响因素进行分析，详细信息如表2所示。

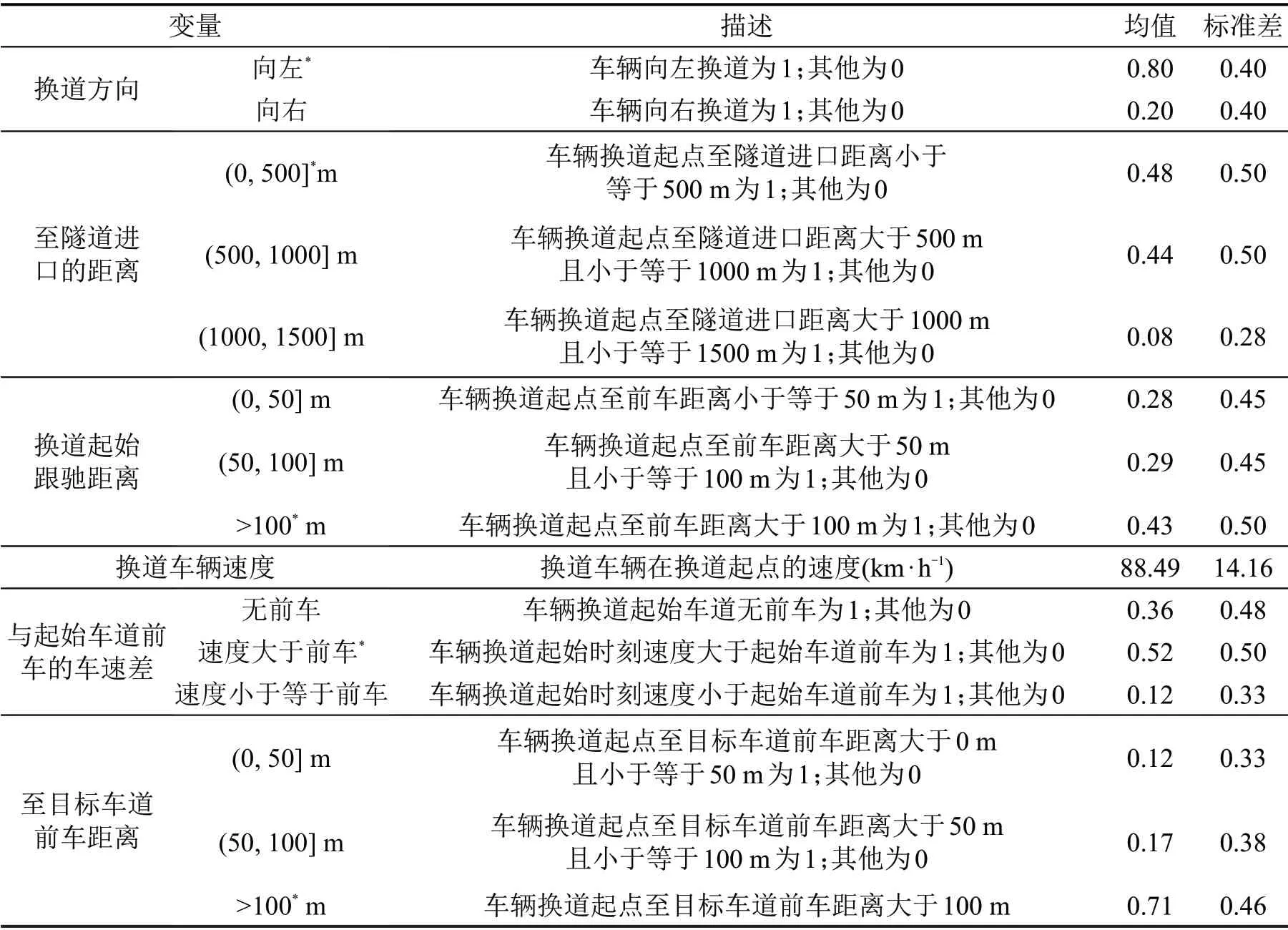
表2 影响因素的描述性统计Table 2 Descriptive statistics of influencing factors

在换道起始跟驰距离方面，依据车辆在开始换道时前方100 m 距离内是否有车辆对车辆的跟驰状态进行判定[11]，将换道起始跟驰距离划分为（0,50]m、（50,100]m和大于100 m这3种类型。

2 车辆换道持续时间生存分析模型

2.1 生存分析理论

生存分析是指根据试验或调查得到的数据对观察对象的生存时间进行分析和推断，研究生存时间和结局与众多影响因素间关系及其程度大小的方法[14]。在车辆换道持续时间分析中，T指从车辆开始换道至车辆驶入目标车道，完成换道为止所持续的时间，生存函数S（t）为车辆换道持续时间T大于t的概率，即

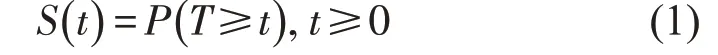
风险函数h（t）表示车辆从开始换道动作，在换道持续时间T达到t时，在接下来单位时间Δt内完成换道的概率，即车辆在换道持续时间t至t+Δt之间完成换道的条件概率，表示为

2.2 全参数估计方法-加速失效时间模型

为研究各变量对车辆换道持续时间的影响，本文使用加速失效时间（AFT）模型（全参数估计方法）进行定量分析。AFT 模型将生存函数S（t）的值对应时间分位数的比值定义为加速因子，并通过加速因子评估协变量对生存时间的影响[14]。AFT 模型中，车辆换道持续时间的自然对数ln（T）表示为协变量的线性函数，即

式中：X′为协变量构成的向量的转置；β为回归系数的向量；ε为扰动项。

AFT模型的生存函数和风险函数分别为

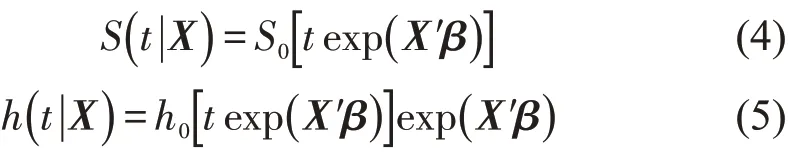
式中：X为协变量构成的向量；h0、S0分别为基准风险函数、基准生存函数。从式（4）和式（5）可以看出，exp（X′β）分别在大于0和小于0时加速、减速车辆换道持续时间。

3 车辆换道持续时间单因素分析

为定量分析在某一特定影响因素下车辆换道持续时间的分布特征，采用Kaplan-Meier方法对车辆换道持续时间的生存函数进行估计，并通过Logrank 和Wilcoxon 检验方法探究不同生存曲线之间的差异性。各分类变量的生存函数曲线如图4所示。

（1）不同位置的换道持续时间分布特征

车辆在高速公路隧道临近段不同位置的换道持续时间生存函数曲线如图4（a）所示。从图4（a）中可以看出，在0～3 s 内3 组生存曲线的变化都较为平缓，说明在隧道临近路段较少车辆于3 s 内完成换道。从3 s开始，3组生存曲线开始出现明显的差异，至隧道进口距离越近，车辆换道持续时间越短。

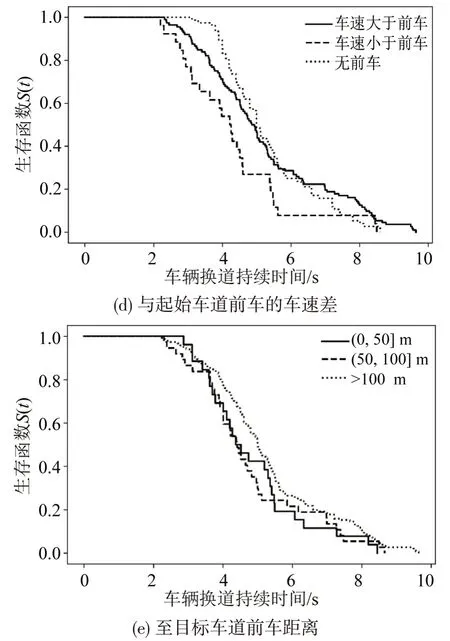
图4 各分类变量的车辆换道持续时间生存曲线Fig.4 Survival curve of lane changing duration for each category variable

通过LogRank 检验和Wilcoxon 检验进行组间比较，发现两种检验方法的结果存在差异，LogRank检验接受原假设（p=0.21），而Wilcoxon检验拒绝原假设（p=0.01）。这主要是由于两种检测方法权重系数不同而导致出现倾向性的差异，Wilcoxon 检验对生存时间较短的个体赋予较大权重，所以更容易检验出早期的差异；而LogRank 检验则更容易发现后期有差异的个体。从该检验结果可以得出：不同路段区间车辆换道持续时间在前期存在较大差异，而后期差异较小。

（2）不同换道方向的换道持续时间分布特征

图4（b）展示了车辆在不同换道方向下车辆换道持续时间的生存曲线变化情况，其中左侧车道为道路内侧车道，右侧车道为道路外侧车道。根据Log Rank 检验与Wilcoxon 检验，p＜0.05，表明两者的换道持续时间存在显著性差异。从图4（b）中可以看出，当时间达到4 s时，不同换道方向的生存曲线差异愈发明显，向右换道的生存曲线更为陡峭，说明向右换道的车辆倾向于在更短的时间内完成换道。

（3）不同换道起始跟驰距离的换道持续时间分布特征

图4（c）展示了换道车辆与起始车道前车处于不同距离情况下的换道持续时间生存曲线变化情况，从约2.7 s 开始，换道车辆在起始车道处于跟驰状态（与前车距离小于100 m）与非跟驰状态（与前车距离大于100 m）的生存曲线开始出现明显差异，车辆处于跟驰状态下的生存曲线下降更快，说明大部分驾驶人处于跟驰状态时趋于更快完成换道操作。而到约5.7 s 时，换道车辆在起始车道跟驰距离处于50～100 m 的生存曲线下降速度减慢。LogRank 检验p=0.04，Wilcoxon 检验p=0.06，表明换道车辆与起始车道前车处于不同距离情况下，车辆换道持续时间在前期差异较小，而在后期存在较大差异。

（4）与起始车道前车不同车速差的换道持续时间分布特征

从图4（d）中可以看出，从约2.5 s 开始，换道车辆车速大于和小于起始车道前车的生存曲线开始发生明显下降，其中换道车辆车速小于起始车道前车的生存曲线下降速率最快，而无前车情况的生存曲线从3.8 s 才开始出现明显下降。依据Log Rank与Wilcoxon 假设检验结果，p＜0.05，表明与起始车道前车不同车速差的换道持续时间存在显著差异。

（5）至目标车道前车不同距离的换道持续时间分布特征

从图4（e）中可以看出，换道车辆与目标车道前车处于不同距离的生存曲线变化趋于一致，同时通过Log Rank 与Wilcoxon 方法进行检验，检验结果皆为p＞0.05，表明至目标车道前车不同距离情况下的换道持续时间没有显著差异。

4 随机参数AFT模型

为了获得式（5）的参数解，需对持续时间进行分布假设，常见的分布包括Weibull，对数正态，Loglogistic 和指数分布[14]。对采集到的高速公路隧道临近段车辆换道持续时间数据进行统计检验，以确定合适的参数化模型，拟合结果如图5所示。

从图5 可以看出，Weibull，对数正态和Loglogistic 分布较为适用。其中，Weibull 分布适用于对风险率单调的数据进行建模，其风险率随时间呈指数级增加或减少，与车辆完成换道的概率随时间的增长而单调上升的情况类似，故本文选用Weibull分布进行模型构建[12]。Weibull分布的AFT模型的风险函数为

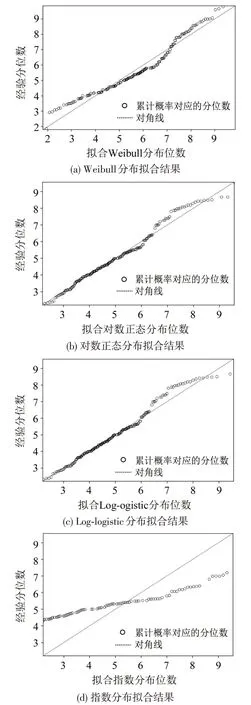
图5 高速公路隧道临近段车辆换道持续时间数据分布拟合结果Fig.5 Data distribution fitting of vehicle LCD in adjacent section of freeway tunnel

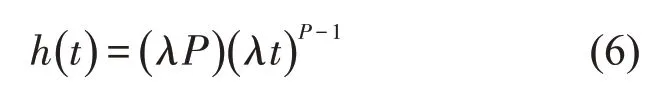
式中：λ为规模参数，λ=exp（X′β）；P为形状参数。

传统AFT 模型假设各因素对车辆换道持续时间的影响是一致的，属于固定参数模型，未考虑不同换道车辆驾驶人个体的异质性。因不同驾驶人年龄、驾驶经验和驾驶风格等方面存在差异，导致不同驾驶人对换道风险的感知能力也不同，同一因素可能对不同驾驶人产生不同的影响，而固定参数AFT 模型难以解释驾驶人异质性对车辆换道持续时间的影响[15]。因此，考虑不同驾驶人对换道风险水平感知的差异，构建随机参数AFT 模型，包含随机参数项的估计参数向量可表示为

式中：βi为第i位驾驶人的参数向量；ui为服从正态分布的异质性随机项。

随机参数AFT模型可表示为

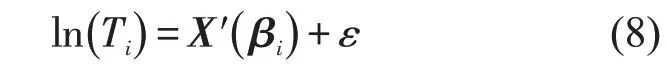
随机参数AFT模型的风险函数为

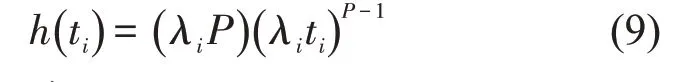
规模参数λi为

本文研究了AFT 模型在随机参数和固定参数两种模式下的应用情况。通过最大似然估计法对固定参数AFT 模型参数进行估计。采用Halton 抽样，基于仿真的最大似然估计法对具有随机参数的AFT 模型进行参数估计，抽样次数取200 次。AFT模型在随机参数和固定参数条件下的参数估计结果如表3所示。

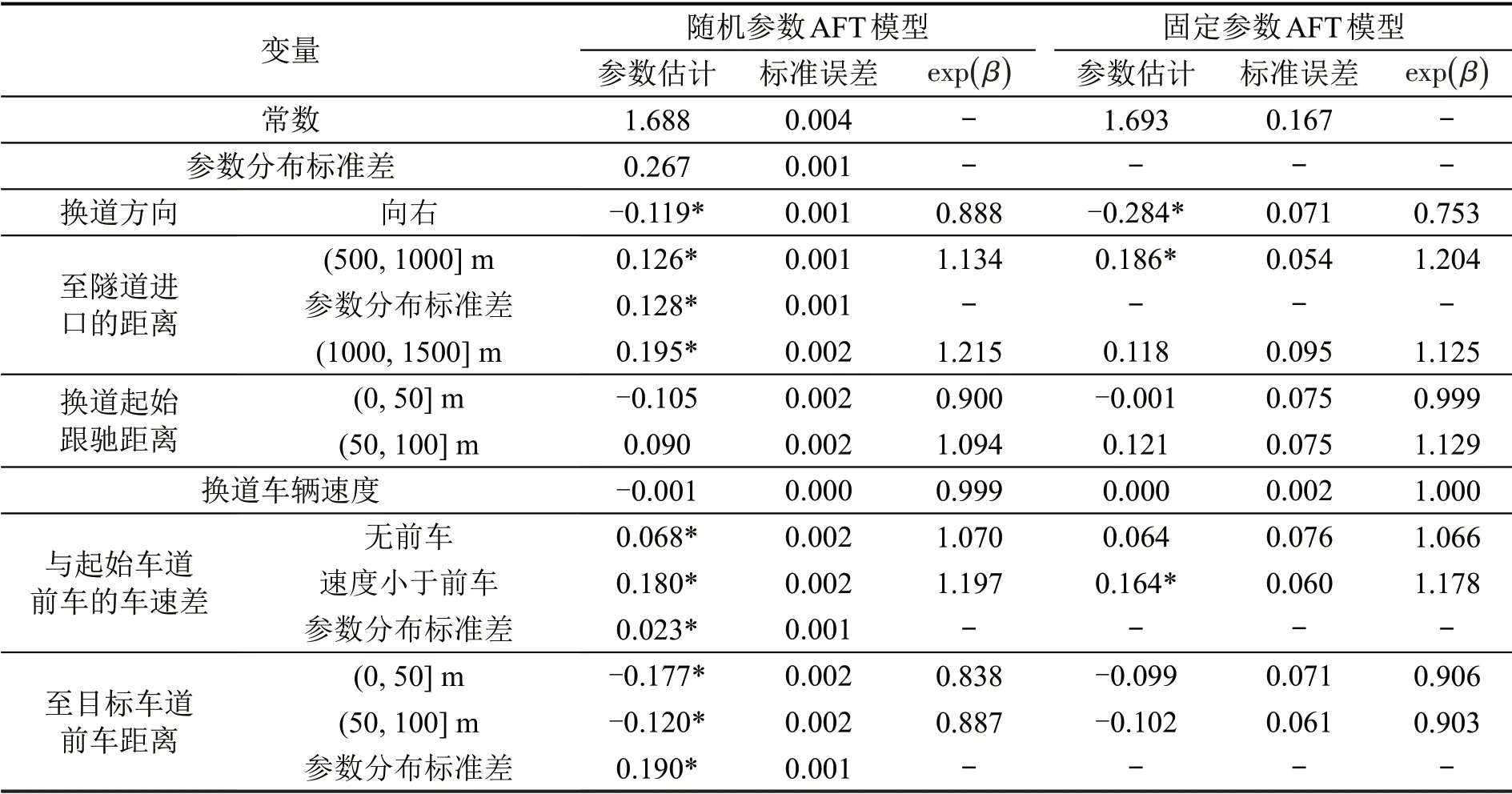
表3 固定参数和随机参数AFT模型估计结果比较Table 3 Comparison of estimation results between AFT model with fixed parameter and random parameter

随机参数AFT 模型识别出3 个具有随机效应的随机参数，分别为：至隧道进口的距离（500,1000] m、至目标车道前车距离（50, 100] m 和起始车道车速小于前车。

从协变量的显著性来看，在随机参数和固定参数AFT模型中，换道车辆速度和换道起始跟驰距离对车辆换道持续时间均无显著影响。与固定参数AFT模型相比，随机参数AFT模型中增加了4个显著变量：至隧道进口距离（1000, 1500] m、无前车、至目标车道前车距离（0,50]m 和（50,100]m，表明随机参数AFT 模型能识别出更多的车辆换道持续时间影响因素。

通过比较两个模型估计结果的对数似然值和AIC，对固定参数和随机参数AFT模型的拟合效果进行验证，结果如表4 所示，发现随机参数AFT 模型优于固定参数的AFT 模型。鉴于随机参数AFT模型的拟合度优于固定参数的AFT模型，本文将基于随机参数AFT模型的参数估计结果进行分析。

表4 固定参数和随机参数AFT模型的模型拟合优度比较Table 4 Comparison of goodness of fit between AFT model with fixed parameter and random parameter

从表3的估计结果中可以看出，在高速公路隧道临近段，换道方向、至隧道进口的距离、与起始车道前车的车速差、至目标车道前车距离这4个变量会对车辆换道持续时间产生显著影响。与向左换道的车辆相比，向右换道的车辆趋于在更短的时间内完成换道，时间降低约11%。从与隧道进口的距离上来看，至隧道进口的距离越远，换道持续时间越长，这可能是当车辆距离隧道进口较远时，换道车辆在进入隧道前有更多的机会进行换道操作来改善自身的行车环境；而当车辆距离隧道较近时，其若需要进行换道，则需要在较短的时间内完成，此时驾驶人可能存在较为“急切”的心理，会采取相对激进的换道策略，造成换道时间较短。相较于至隧道进口距离（0,500]m 的情况，至隧道进口距离（500,1000]m 和（1000,1500]m 情境下的换道时间分别增加约13%和21%。

在换道车辆与前车的相对运动状态方面，当换道车辆车速高于起始车道前车时，换道车辆人趋于在更短的时间内完成换道，这可能与驾驶人的驾驶风格有关。当前车的车速较低，不能满足驾驶人对速度的需求时，其往往会采取换道措施来寻求更好的驾驶体验，而这类驾驶人的驾驶策略相对激进，换道持续时间普遍偏短。换道车辆与目标车道前车距离越近，换道持续时间越短，相较于至目标车道前车距离大于100 m的情况，至目标车道前车距离（0,50]m和（50,100]m时的换道持续时间分别降低约16%和11%。这可能与换道车辆周边交通环境的复杂度有关，当周边车辆较多时，驾驶人采取更短时间完成换道的策略可以减少对周边车辆影响的时间，从而降低行车风险；而当至目标车道前车距离较远时，车辆换道过程对周边车辆的影响相对较小，驾驶人可以采取更为“温和”的换道策略提升驾车体验，从而造成换道持续时间的增加。

5 结论

（1）高速公路隧道临近段不同位置、不同换道方向、与起始车道前车不同车速差和跟驰距离情况下的车辆换道持续时间存在显著差异。

（2）相较于固定参数AFT 模型，构建的随机参数AFT模型的拟合效果更优。

（3）从随机参数AFT 模型得到的估计结果来看，换道车辆的车速与换道起始跟驰距离对车辆换道持续时间均没有显著影响。向右换道、与隧道进口距离越近、换道车速度大于起始车道前车、至目标车道前车距离的降低都会减少高速公路隧道临近段车辆的换道持续时间。