横梁移动式五轴龙门铣床摆动轴与位置相关的几何误差检测与辨识＊

邬昌军 郑明明 王巧花 范晋伟 王良文 宋晓辉

（①郑州轻工业大学河南省机械装备智能制造重点实验室，河南 郑州 450002；②北京工业大学北京先进制造技术重点实验室，北京 100124；③河南省科学院，河南 郑州 450008）

五轴机床作为“工作母机”具有更高的加工效率、更快的切削速度和更强的加工能力[1]，但其两个旋转轴的存在带来更多几何误差将直接影响机床加工精度[2-3]。横梁移动式五轴龙门铣床是一种适应于大型、重型工件的双摆头（回转轴和摆动轴）五轴机床，加工行程长、龙门跨度大，无需移动工件便可以实现复杂曲面的数控加工。然而，受长行程、大跨度及高负载因素影响，横梁在重力作用下易变形，导致机床各部件之间的位置关系发生变化，严重影响加工精度[4]，而其摆动轴B轴作为机床传动链的最末端，直接与刀具相连。因此，摆动轴与位置相关的几何误差的检测与辨识对提高大型五轴机床的加工精度具有非常重要的意义[5-7]。

近年来，国内外学者们对多轴数控机床旋转轴的几何误差进行了诸多方法的检测与辨识。Xia H J等[6]用减小球杆仪的安装误差的方法，提高了回转轴几何误差测量的准确性，但其测量方法过于复杂。Li Q Z等[7]用球杆仪识别了一种倾斜式双转台型五轴机床旋转轴的几何误差，但球杆仪的安装位置有一定的局限性，易引起与工作台的碰撞。Chen D J等[8]利用球杆仪辨识出旋转轴B轴4项与位置相关的几何误差，缺少两项角位移误差。夏长久等[9]提出了一种基于球杆仪单轴运动测量的旋转轴几何误差辨识方法，但其旋转轴的角定位误差未深入分析。Ibaraki S等[10]提出了用R-test来自动辨识旋转轴与位置相关的几何误差的方法。李国龙等[11]用球杆仪6种安装模式，快速测量小型HMU20 五轴加工中心转台C轴6项与位置相关的几何误差。Uddin M S等[12]利用球杆仪对机床旋转轴与位置无关的几何误差进行了识别。项四通等[13]提出了3种基于球杆仪测量和辨识旋转轴误差的测量方法，通过不同的测量模式辨识出Quaser UX600 双转台五轴数控机床旋转轴的几何误差，但没有考虑误差之间的耦合影响。

由于雷尼绍XR20-W测量装置即使无法安装在摆动轴旋转轴线上也可实现角定位误差的准确测量[13]。考虑到摆动轴各几何误差间的耦合影响，首先由雷尼绍XR20-W测量装置直接测量摆动轴角定位误差，然后利用多体系统运动学理论建立机床摆动轴(B轴)运动学模型；基于角定位误差，通过球杆仪一次安装辨识出机床摆动轴其余5项与位置相关的几何误差。最后，通过对检测辨识结果进行回归分析和对比分析，以验证所提出的摆动轴几何误差检测与辨识方法的可靠有效性和辨识结果的正确性。

1 横梁移动式五轴联动龙门铣床结构

如图1所示，研究机床为XKAS2525×60型横梁移动式五轴联动龙门铣床，主要包括放置加工工件W的工作台1，在工作台上沿X轴方向滑行的横梁2，在横梁侧方沿Y轴方向移动的鞍座3，在鞍座单侧面沿Z轴方向滑动的滑枕4，绕Z轴旋转的回转轴5（C轴），绕Y轴摆动的摆动轴6（B轴），刀具T在B轴下端。

2 摆动轴的几何误差定义

根据ISO 230-7[15]，摆动轴的几何误差分为与位置无关的几何误差(PIGEs)和与位置相关的几何误差(PDGEs)，如表1所示。PIGEs主要产生于零部件装配过程中，它们不随轴类部件运动而变化。

表1 B轴几何误差分类

图2为PIGEs的示意图，其中，X、Z轴为B轴参考基准轴，B′为B轴实际方向， εxb和 εzb分别为摆轴B与平动轴X、Z间的垂直度误差。PDGEs主要因自身加工缺陷引起，它们随轴类部件运动而变化；B轴有6个自由度，分别为3个平动自由度和3个转动自由度，每个自由度分别对应一项几何误差。

图2 与位置无关的几何误差

如图3所示， εx(b)、 εy(b)、 εz(b)分别为B轴绕X、Y、Z轴运动的角位移误差， δx(b)、 δy(b)、δz(b)分别为B轴在X、Y、Z方向上引起的线位移误差。

图3 与位置相关的几何误差

3 摆动轴运动学分析建模

根据文献[16-19]，多体系统理论通过分析相邻物体之间的相对运动关系，将一个复杂的力学系统划分为几个独立的物体，并对整个运动系统进行描述，且机床可视为由许多刚体组成[16]。如图4所示，物体6（B轴）和5（C轴）彼此相连，物体6相对于物体5转动过程中存在几何误差，使物体6偏离理想位置。O6-X6Y6Z6和O5-X5Y5Z5分别为物体6和5上的坐标系；Ql6和Q6分别为物体5体参考坐标系中物体6的理想运动参考点和实际运动参考点；ql6和q6分别为理想位置矢量和实际位置矢量；qe6为位置误差矢量；Ol6和O6分别为物体6体参考坐标系原点在实际运动参考坐标系中的理想运动位置和实际运动位置；sl6和s6分别为理想运动矢量和实际运动矢量；se6为运动误差矢量；Hb为物体6上固定点D′b在物体6体坐标系中的位置矢量。

2)与Weibull(韦伯分布)函数相关系数的计算。生成3 180×1的韦伯分布随机矩阵数据，然后以z=corrcoef(A,C)指令计算相关系数，zWeibull=0.002 1。

图4 相邻体相对运动示意图

物体6在物体5体坐标系中的任意点D′b的位置方程可以用以下方程表示

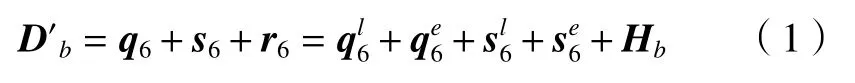
转化为实际位置矩阵表达式为

式中：

D′b为点Dbx在物体5体坐标系O5-X5Y5Z5中的实际位置矩阵； {Hb}为Db在坐标系O6-X6Y6Z6中的位置矩阵； [S56]p为物体6相对物体5的相对位置矩阵；[S56]pe为物体6相对物体5的位置误差矩阵；[S56]s为物体6相对物体5的相对运动变换矩阵；[S56]se为物体6相对物体5的运动误差变换矩阵。

物体6绕物体5做旋转运动，Db为Dbx点在物体5体坐标系坐标系O5-X5Y5Z5中的理想位置矩阵

理想位置与实际位置之间的误差表达式为

4 B轴几何误差测量与辨识

4.1 基于球杆仪的测量原理

球杆仪检测系统如图5所示，其中有一测量杆，测量杆两端有两个球体（中心球1和中心球2）分别安装在工具杯和中心杯上，工具杯被机床主轴卡紧，中心杯被中心座卡紧。球杆仪测量系统中的测量杆可以伸缩变换，里面装有高精度传感器，B轴运动时，该传感器可以捕捉到两球中心位置之间的微小误差。

图5 双球杆仪的结构图

摆动轴的8项几何误差中，角定位误差 εy(b)由雷尼绍XR20-W测量装置直接测量，垂直度误差 εxb、εzb可依据ISO 10791-2[20]附录中所述的检测方法检测，其余5项与位置相关的几何误差需要球杆仪间接识别。

4.2 基于齐次变换矩阵的误差辨识模型

识别B轴的几何误差分4种模式进行,分别为BX模式、B-Z模式、B-Y模式、B-XY模式，依次对B轴X、Z、Y、X的4个方向进行检测。球杆仪的方向配合机床体坐标方向，B轴的体坐标系原点位于B、C轴轴心线交汇处，B轴的坐标系方向受C轴影响，为单独研究B轴，B轴体坐标系名称不变，计算过程中B轴体坐标系方向配合球杆仪坐标系进行变换，B轴的变换位姿用4×4齐次变换矩阵表示。

图6为测量模型在XZ平面上的简化图，Pb为B轴理想体坐标系原点，P′b为B轴体坐标系原点实际位置，Dbx为小球的理想位置，D′bx为小球的实际位置， Δx为B轴定位误差在Z方向投影， Δ β为B轴在XZ平面上的角度误差，Hb为B轴理想体坐标系原点到小球理想位置的距离， ΔLbx为小球的实际位置到小球的理想位置的距离。B轴运动时，在角度和位置误差的影响下，B轴会在Z方向上产生误差。

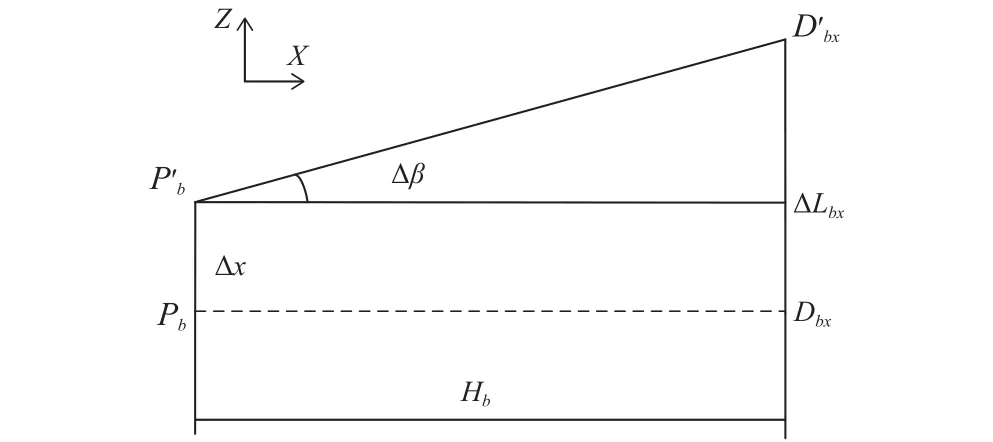
图6 B-X 测量模式误差产生原理

4.2.1B-X模式

令C轴与机床Z轴保持平行，球杆仪保持水平180°，仅B轴运动，X、Z轴做跟随运动，测量球杆仪在X方向的长度变化。让B轴体坐标原点在它的回转中心处，即B轴和C轴中心线的交点，Pb到Dbx的理论距离为Hb1。由于球杆仪和B轴运动轨迹会互相干涉，B-X模式测量过程分为B-X-N和BX-P两部分进行，且B-X-N测量模式里B轴回转角度为负值；B-X-P测量模式里B轴回转角度为正值,如图7所示。

图7 B-X 模式示意图

小球在B轴体坐标系中的理想位置Db可由式（5）表示；小球在B轴体坐标系中的实际位置D′b可由式（6）表示；球杆仪长在X方向的变化量可由式（7）表示；将式（7）进行整理，可得到式（8），εxc、 εy(b)为已知误差参数，所以式（8）中还有两项未知误差参数，需进一步建立辨识方程求解。

4.2.2B-Z模式

令C轴与机床Z轴保持平行，球杆仪保持水平180°，仅B轴运动，X、Z轴做跟随运动，测量球杆仪在Z方向的长度变化，Pb到Dbz的理论距离为Hb1，如图8所示。

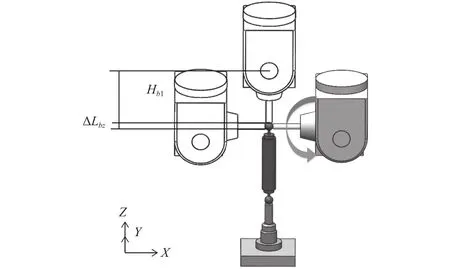
图8 B-Z 模式示意图

由式（6）可得球杆仪在Z方向上的杆长变化，即式（9）；参数 εxc、 εy(b)为已知误差参数，将式（9）进行整理，可得式（10）；式（10）包含δz(b)、 δx(b)两项未知数，联立（8）可得式（11），化简式（11）求得 δz(b)、 δx(b)。

由式（6）可得球杆仪在Y方向上的杆长变化，即式（14），将式（14）进行整理，得到式（15），参 数 εyc、 εbz、 εxb为 已 知 误 差 参 数 ， 即 式 （15） 中还有两项未知误差参数，需进一步建立辨识方程求解。

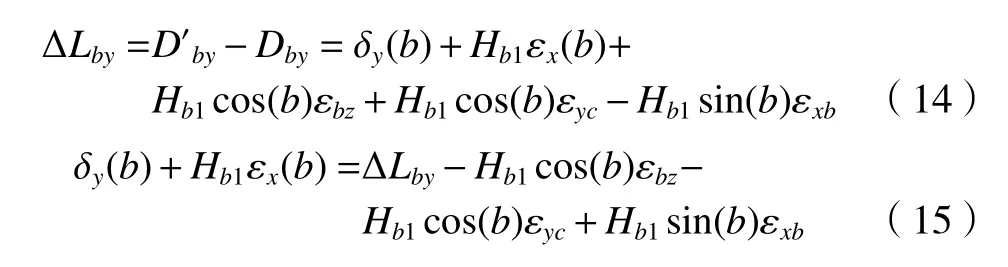
4.2.3B-Y模式

令C轴与机床Z轴保持平行,球杆仪保持水平180°，仅B轴运动，X、Z轴做跟随运动，测量球杆仪在Y方向的长度变化。

在B-Y-1测量模式中，设B轴原点Pb到小球理想位置Dby1的距离为Hb1，小球的实际位置在D′by1；在B-Y-2测量模式中，设B轴原点Pb到小球理想位置Dby2的距离为Hb2,小球的实际位置在D′by2，如图9所示。

图9 B-Y 模式示意图

由式（15）可得方程（16），解方程得 εx(b)、δy(b)。

4.2.4B-XY模式

在B-X测量模式的基础上，令球杆仪固定杆沿Y轴正向偏移Hby后固定，如图10所示。令C轴与机床Z轴保持平行,球杆仪保持水平180°，仅B轴运动，X、Z轴做跟随运动，测量球杆仪在X方向的长度变化，Pb到 小球理想位置Dbx的距离为Hb3，小球的实际位置在D′bx。

由于球杆仪和B轴的运动轨迹会互相干涉，因此，B-XY模式测量过程分为B-XY-N和B-XY-P两部分进行，且B-XY-N测量模式里B轴回转角度为负值；B-XY-P测量模式里B轴回转角度为正值，如图10所示。

图10 B-XY 模式示意图

小球在B轴体坐标系中的理想位置Db可由式（19）表示；小球在B轴体坐标系中的实际位置D′b可由式（20）表示；球杆仪长在X方向的变化量可由式（21）表示；整理式（21）可得 εz(b)。

5 误差测量实验

如图11所示，用雷尼绍XR20-W校准装置直接测得角定位误差 εy(b)。依据 ISO 10 791-2[15]附录中所述的检测方法，获得相关垂直度误差，如表2所示。其余5项几何误差辨识设备为雷尼绍QC20-W球杆仪，主要技术参数如表3所示。

表2 垂直度误差

表3 雷尼绍QC20-W球杆仪检测系统性能指标

图11 XR20-W 检测

如图12所示，球杆仪精确安装，取Hb1=690 mm，Hb2=790 mm，Hb3=890 mm，Hby=60 mm，B轴误差测量行程共为210°，每隔15°采集一次误差，且行程最小值为-105°，最大值为105°，共15个误差采集点，每一测量行程往返测量5次，将每一测量点处采集到的杆长变化量取平均值。4种模式的球杆仪运行轨迹如图13所示，其中黑线为误差影响下的轨迹，灰线为理想运动轨迹；测量轨迹偏心率如表4所示。

表4 偏心率

图12 球杆仪检测

图13 球杆仪测量运动轨迹图

将以上数据代入式（14）、（15）、（19）、（20）、 （26）中，获得 δx(b)、 δz(b)、 εx(b)、δy(b)和 εz(b)等5项误差。

由于机床的几何误差参数与部件的运动行程间存在着周期性的作用规律，但同时存在一些不确定的因素。因此，利用傅里叶级数[21]模型拟合误差测量辨识结果，采用高斯-牛顿迭代法计算模型的回归系数，得到机床单项几何误差参数拟合曲线。

以角定位误差 εy(B)和Y向跳动误差 δy(B)为例，以验证B轴误差测量辨识结果的可靠性。

εy(B)的拟合曲线如图14所示，辨识点残差平方和SSE=1.065 0× 10-11，拟合曲线确定系数R2=0.975 3。δy(B)的拟合曲线如图15所示，辨识点残差平方和SSE=2.783 8×10-10，拟合曲线确定系数R2=0.997 8。

图14 B 轴角定位误差εy(B)

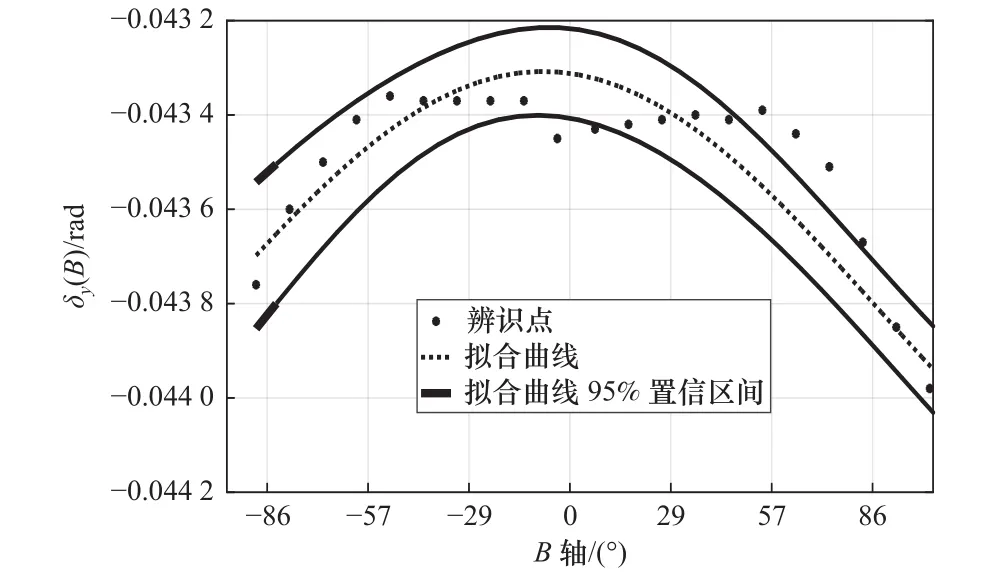
图15 B 轴的 Y 向跳动误差δy(B)

从图中可以看出摆动轴几何误差检测辨识结果良好，可以反映各几何误差参数的运动规律，从而证明所提出的摆动轴轴单项几何误差检测与辨识方法是可靠有效的。

为进一步验证辨识结果的正确性，首先利用文献[16]介绍的方法对检测和辨识的摆动轴几何误差进行补偿，然后利用Renishaw QC20-W球杆仪测量ZX平面内形成的圆形轨迹，并将这一轨迹与标准圆形轨迹进行比较（如图16所示）。表5为误差补偿前后的圆形轨迹圆度比较。根据表5，补偿前后的圆度减少了57.5%，从而说明了摆动轴几何误差辨识结果的正确性。

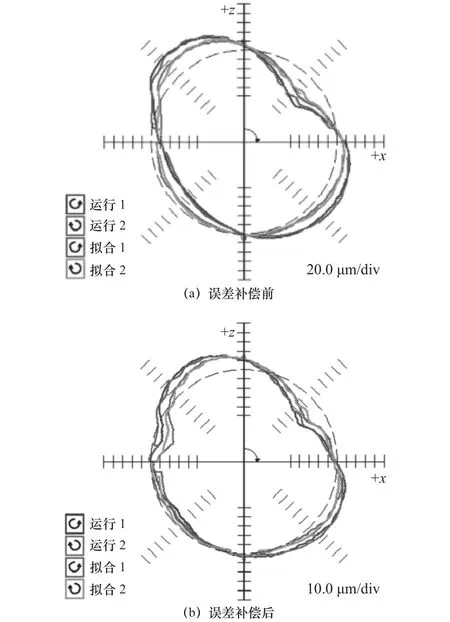
图16 球杆仪在 ZX 面的测量结果

表5 圆度比较

6 结语

本文提出了一种XKAS2525×60大型五轴龙门铣床摆动轴B轴6项与位置相关的几何误差检测与辨识方法，首先基于多体系统运动学理论建立机床摆动轴B轴运动学模型，然后基于球杆仪建立机床摆动轴B轴5项几何误差辨识模型。最后，基于雷尼绍XR20-W校准装置测得角定位误差和利用球杆仪辨识出B轴其余5项与位置相关的几何误差，并对实验结果进行回归分析和对比分析，实验结果表明：所提出的机床摆动轴几何误差检测与辨识方法简化了大型机床旋转轴检测和辨识过程、提高了测量精度和效率，检测与辨识结果是可靠有效和正确的。