半椭球形微凸体的结合面接触热导分形模型＊

赵海路 张学良 许雍泰

（太原科技大学机械工程学院，山西 太原 030024）

机械设备在长时间的运转下，必然会产生大量的热量，而当这部分热量从一个零件传到另一个零件时，由于零件之间表面接触不完全而导致热流线收缩，此时交界面会产生明显的温度差，从而会导致不同的接触热导（TCC）。热流的主要导热方式有[1]：两物体表面之间相互接触微凸体的热传导；两物体表面间隙介质的热传导；两物体表面的热辐射。随着现代科技的发展，接触热导在机械制造、航空航天、低温超导和热交换器等领域发挥着越来越重要的影响[2]。

自20世纪60年代以来，许多学者从理论、实验和数值分析等方面对接触热导进行了深入的研究。1969年，Cooper M G等[3]提出了第一个接触热阻模型，即CMY模型，为以后的学者研究接触热导和接触热阻奠定了基础。Zou M Q等[4]提出了一个基于分形几何理论的随机数值模型来计算接触热导，发现分形参数D和G对接触热导有显著影响。Zhang J H等[5]研究了考虑微凸体弹塑性变形和基体热阻的接触热导预测分形模型，计算了包括基体在内的接触热阻。马丽娜[6]建立了接触热导的二维分形模型，并分析了分形维数、法向载荷对热导的影响。Jeng Y R等[7]提出了一种考虑弹性、弹塑性和塑性变形的椭球形微凸体接触模型，建立了平均接触压力与微凸体接触面积及变形量之间的关系。谭文兵等[8]依据各向异性分形几何理论，将微凸体接触面拓展为椭圆形，推导出包含偏心率在内的椭圆形接触面面积的二维联合分布密度函数并建立了基于椭球形微凸体的结合面法向接触刚度模型。

然而，现有结合面接触热导分形模型研究的不足之处在于都将微凸体理想化为半球形，这与实际情况并不相符，而且已有研究表明[9-11]，将微凸体接触面拓展为半椭圆形，这样更加符合实际情况，也更具有一般性。且有关微凸体为半椭球形的结合面接触热导问题还无人研究，故本文建立了考虑半椭球形微凸体弹性、弹塑性和塑性接触变形机制的结合面接触热导三维分形模型，并研究了相关参数对所建模型的影响。

1 半椭球形微凸体接触模型

结合面问题可以等效简化为一个当量粗糙表面和一个理想刚性平面的接触问题，如图1所示，p为单个半椭球形微凸体所受的法向载荷，接触长度为l=2b， δ为微凸体的变形量，微凸体实际接触面积s= πab，a、b、e分 别 为 微 接 触 椭 圆 面 的长 、 短半轴长和偏心率，且

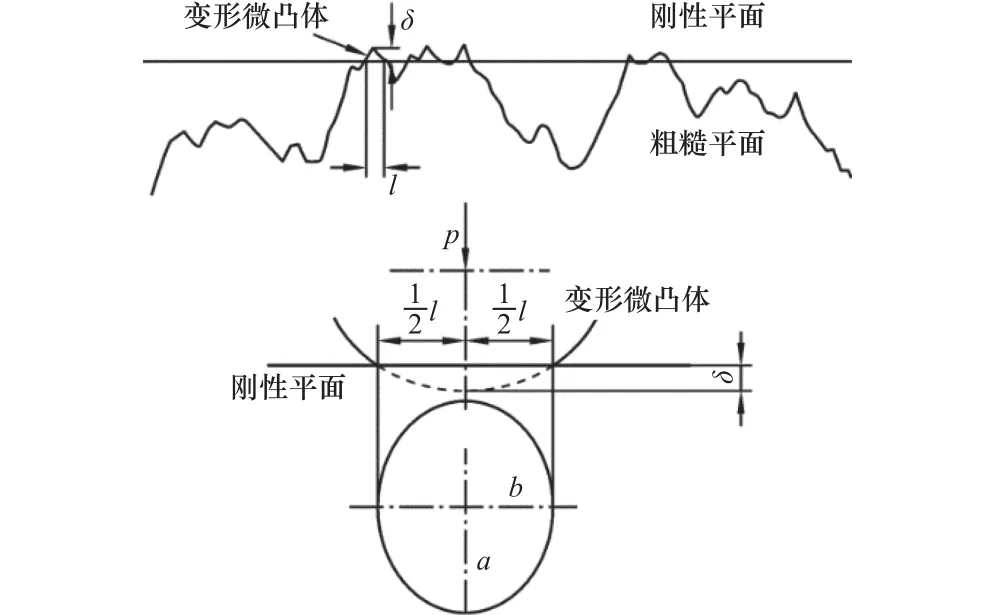
图1 半椭球形微凸体与刚性平面接触模型

1.1 半椭球形微凸体弹性接触

半椭球形微凸体的变形量为[12]

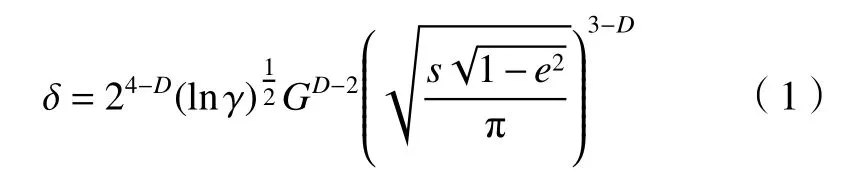
由文献[12]可知，当半椭球形微凸体法向变形量为 δ时，其弹性变形下对应的接触面积se，所受的法向载荷pe， 曲率半径Rm，分别为

式中：D为 分形维数；G为分形粗糙度参数；E为等效弹性模量，，E1、E2分别为两接触材料的弹性模量，v1、v2分别为两接触材料的泊松比；，其中K(e)、E(e)分别为第一和第二类椭圆积分：K(e)=

1.2 半椭球形微凸体弹塑性接触

半椭球形微凸体开始产生塑性屈服的临界变形量 δc为[12]

式中：H=2.8σy， σy为较软材料的屈服极限；材料特性参数；K为硬度系数，与较软材料的泊松比v之间的关系为K=0.454+0.41v。

当 δ = δc时，联立式（1）和式（5）可得相应的弹性临界微接触面积sc(e)与偏心率e满足的关系为

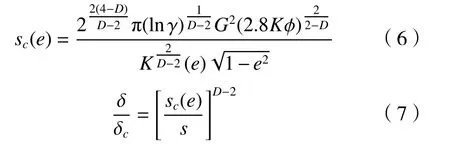
当半椭球形微凸体的变形量 δ满足 δc≤ δ≤ 6δc，即sepc≤s≤sc时（sepc为第一弹塑性临界微接触面积），微凸体发生第一弹塑性变形，其对应的第一弹塑性接触面积和接触载荷分别为[12]

此外，当半椭球形微凸体的变形量 δ满足6δc≤δ≤ 110δc，即spc≤s≤sepc时（spc为第二弹塑性临界微接触面积），微凸体发生第二弹塑性变形，其对应的第二弹塑性接触面积和接触载荷分别为[12]

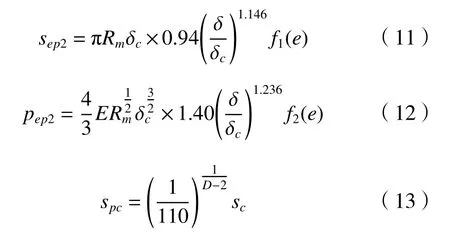
1.3 半椭球形微凸体塑性接触

当半椭球形微凸体的变形量δ满足 δ ≥ 110δc，0≤s≤sp时，微凸体发生塑性变形，此时微凸体接触面积与接触载荷分别为[7]

2 基于半椭球形微凸体的结合面接触模型

由于只将微凸体的形状由原来的半球形拓展为半椭球形，而结合面上的微凸体面积大小分布密度却没有变化，故将具有分形特征的结合面半椭球形微凸体的面积大小分布密度函数采用与半球形微凸体的面积大小分布密度函数[13]相同的形式。

式中： ψ为域扩展因子；sl为微凸体的最大接触面积，其中Ar为结合面真实接触面积。

2.1 结合面弹性接触载荷

由式（3）和式 （16）可得，结合面弹性接触载荷为

将式（17）和式（18）进行无量纲化，当D≠2.5时，

当D=2.5时，

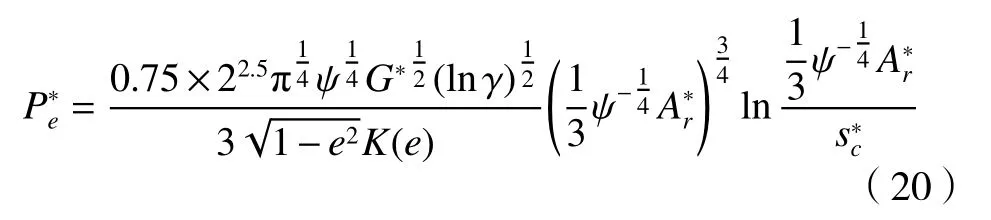
式（19）和式（20）中：G*为无量纲分形粗糙度参数；为接触率；为无量纲弹性临界微接触面积。

2.2 结合面弹塑性接触载荷

由式（9）和式（16）可得，结合面第一弹塑性接触载荷为

对式（21）进行无量纲化得

由式（12）和式（16）可得，结合面第二弹塑性接触载荷为

对式（23）进行无量纲化得

结合面弹塑性接触载荷为

从而结合面无量纲弹塑性接触载荷为

2.3 结合面塑性接触载荷

由式 （15） 和式 （16） 可得，结合面塑性接触载荷为

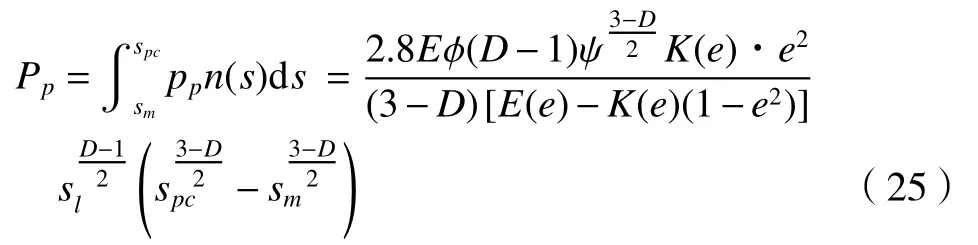
式（25）中：e为偏心率。

对式（25）进行无量纲化得

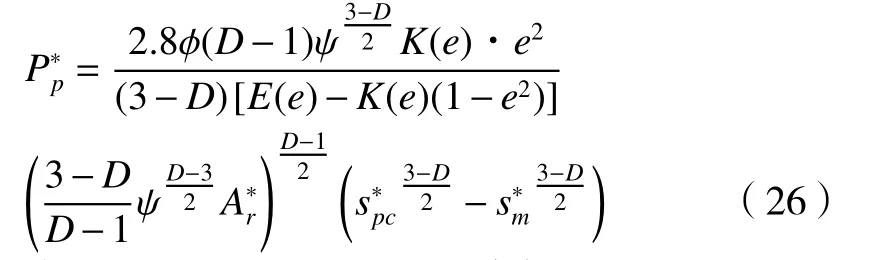
综上可得，考虑半椭球形微凸体弹性、弹塑性和塑性3种接触变形机制的结合面无量纲接触载荷为

3 基于半椭球形微凸体的结合面接触热导模型

3.1 半椭球形微凸体的接触热导模型

由文献[14]中单个半球形微凸体的接触热导公式可以推导出单个半椭球形微凸体的接触热导公式为

从而可得，半椭球形微凸体的弹性接触热导、第一弹塑性接触热导、第二弹塑性接触热导和塑性接触热导分别为

式中： λ为结合面导热系数， λ1和 λ2分别为两接触材料的导热系数。

3.2 结合面接触热导模型

由式（16） 和式 （29） 可得，结合面弹性接触热导为

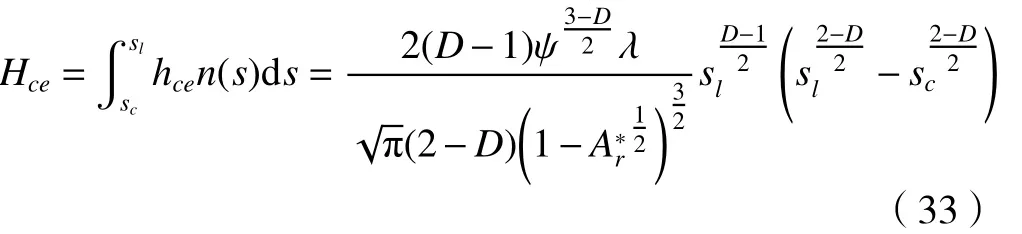
对式（33）进行无量纲化得

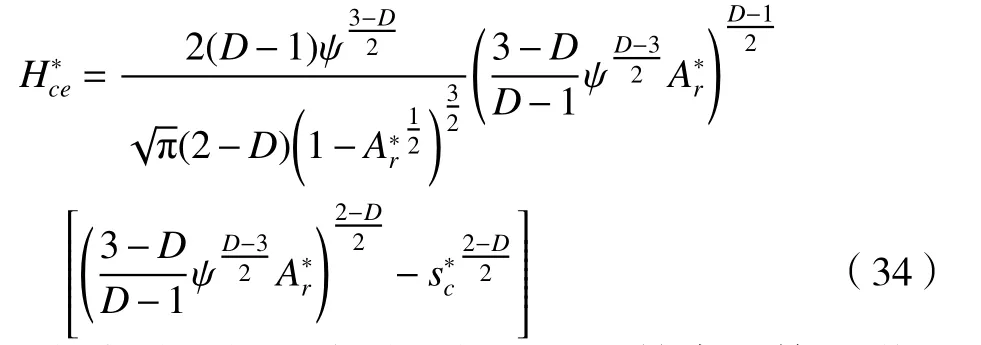
由式（16）和式（30）可得，结合面第一弹塑性接触热导为

对式（35）进行无量纲化得

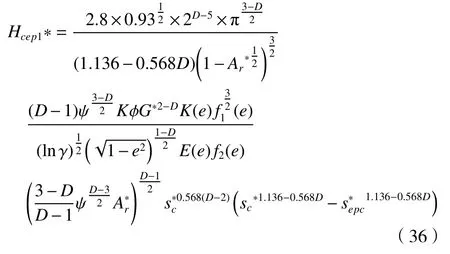
由式（16）和式（31）可得，结合面第二弹塑性接触热导为

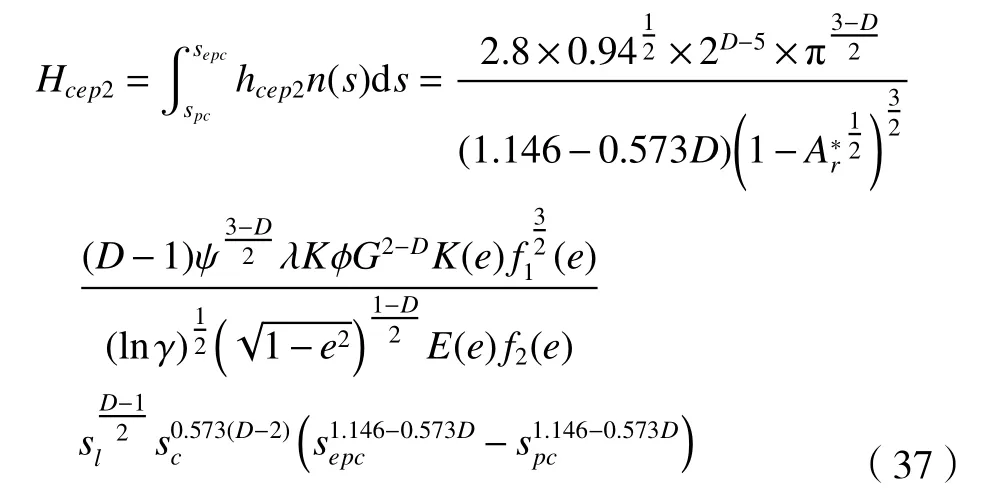
对式（37）进行无量纲化得

由式（16）和式 （32） 可得，结合面塑性接触热导为

对式（39）进行无量纲化得

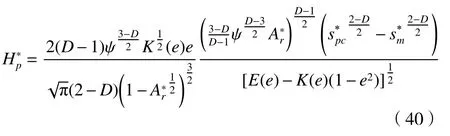
综上可得，考虑半椭球形微凸体弹性、弹塑性和塑性3种接触变形机制的结合面无量纲接触热导为

3.3 建模流程

为了便于从整体上理解和把握以上所建半椭球形微凸体的结合面接触热导模型的理论推导过程，建模流程如图2所示。

图2 建模流程图

4 结合面接触热导模型的仿真分析

取=0～0.02，分形维数D=2.1～2.9，偏心率e=0.1～0.9，无量纲化分形粗糙度参数G*=10-11～10-9，对式（27）和式（41）所建模型进行仿真计算，结果如图3～6所示。

图3 D 对 的影响(e=0.5,φ=1.5)

4.1 分形维数 D对接触热导的影响

为了便于分析分形维数D对 无量纲接触热导的影响，这里将对采用对数坐标的形式。

由图3可知，结合面之间的接触热导随着分形维数D的 增大而增大。这是因为随着D的不断增大，从微观上讲，将导致两表面之间相互接触的椭球形微凸体数目变得越来越多，从宏观上讲，两接触表面将表现为越来越光滑，从而使结合面接触面积越来越大，故无量纲接触热导也就越来越大。

4.2 偏心率 e和对接触热导的影响

图4 e 和 对的影响(φ=1.5,D=2.3)

由图5可知，在不同的分形维数D下，结合面接触热导都随着无量纲化法向载荷P*的增大而增大；在P*和D一 定时，结合面无量纲化接触热导随着无量纲化分形粗糙度参数G*的增大而减小。这主要是因为，P*越大，从图5c可知，结合面接触面积越大，故越大；而在P*和D一 定时，随着G*的不

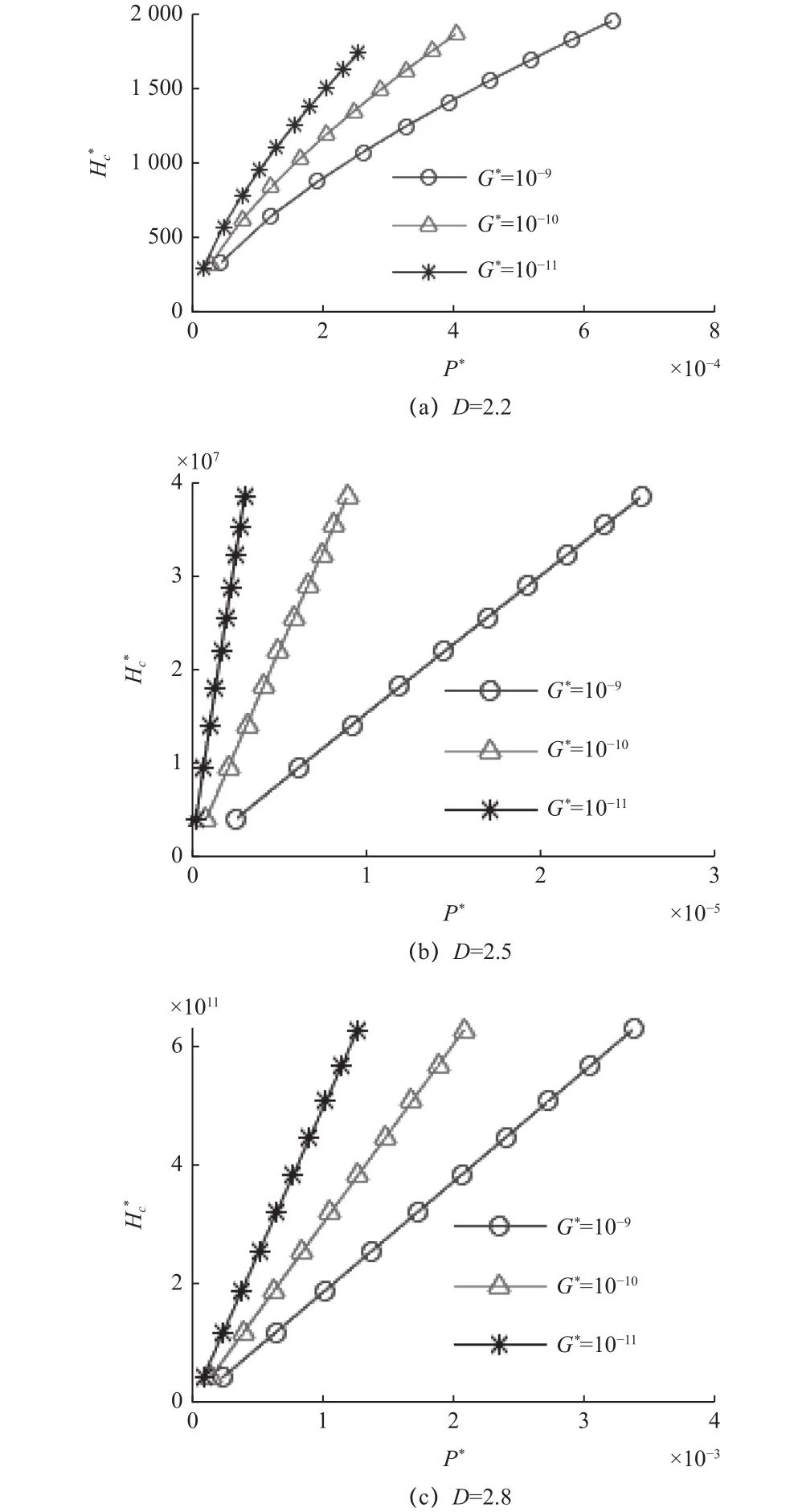
图5 P*和 G *对 的影响(e=0.5,φ=1.5)

4.4 两种接触热导模型的对比

如图6所示，Semiellipsoid表示基于半椭球形微凸体的结合面接触热导模型(即本文所建模型)，记为模型1；Semisphere表示以往的基于半球形微凸体的结合面接触热导模型，记为模型2。

由图6可知，当分形维数D和分形粗糙度参数G*一定时，模型1和模型2所仿真出来的结合面无量纲接触热导都随着无量纲法向载荷P*的增大而增大；且当P*一定时，随着分形维数D的不断增大，模型2的总要比模型1的大。断增大，结合面越粗糙，结合面之间相互接触的微凸体减少，故越小。

图6 两种接触热导模型的对比(G*=1e-9)

5 结合面接触热导模型的验证

为了验证所建模型的正确性，采用文献[5]的实验数据，两接触材料采用304不锈钢，其中分形维数D=2.8567，分形粗糙度参数G=5.112×10-7m，热导率 λ =10.7W/(mK)，弹性模量E1=E2=201GPa，截断长度Ls=1nm ，泊松比v1=v2=0.28，材料的硬度H=2400MPa ；并取偏心率e=0.3，将以上参数数据代入本文所建模型，其仿真计算结果与实验数据的对比如图7所示。

由图7可知，在法向压力P＞3MPa 时，本文所建基于椭球形微凸体的结合面接触热导模型的仿真计算结果与实验数据吻合较好，而在法向压力P≤3MPa时，本文所建模型的仿真计算结果与实验值偏差较大；这主要是因为本文预测模型忽略了相邻非接触微凸体间隙的介质热传导，尤其是在低法向压力条件下，实际接触面积只占名义接触面积的很小一部分，即此时相邻非接触微凸体间隙的介质热传导起着较大的主导作用，从而会出现上述在低法向压力下预测数据要小于实验数据的现象，因此从总体上说，本文所建的基于椭球形微凸体的结合面接触热导模型是正确可信的。

图7 本文模型与球形模型及实验数据的对比

此外，从图7中还可以看出，当法向压力P＞6MPa 时，本文模型的Hc要比半球形微凸体的结合面接触热导Hc更接近实验数据，从而说明在法向压力较大时，本文所建的半椭球形微凸体的结合面接触热导模型要优于半球形微凸体的结合面接触热导模型。

6 结语

本文将结合面之间的微凸体从半球形拓展为半椭球形，弥补了以往接触热导模型中将微凸体理想化为半球形的不足，在此基础上，基于三维分形接触理论，建立了考虑半椭球形微凸体弹性、弹塑性和塑性3种变形机制的结合面接触热导模型，仿真结果表明：

（1）半椭球形微凸体的结合面无量纲接触热导随着椭圆偏心率、分形维数、无量纲法向载荷和接触率的增大而增大，而随着无量纲分形粗糙度参数的增大而减小。

（2）半椭球形微凸体的结合面接触热导模型较于半球形微凸体的结合面接触热导模型更适用于法向载荷较大的情况；所建模型的仿真计算结果与实验数据的一致性验证了本模型的正确性。