全面剖析高频考点化学平衡常数的计算

湖北 张莉华 杨世全

化学平衡常数是化学平衡模块中的一个重要知识点，为电离平衡、水解平衡、沉淀的溶解平衡等理论的学习奠定了基础。化学平衡常数的应用与日常生产生活联系也十分紧密，如判断反应进行的程度、判断反应的热效应、计算反应物的转化率、指定物质的百分含量等，同时也对实际生产条件的选择和控制有指导作用。在《普通高中化学课程标准(2017年版2020年修订)》背景下，高考命题由“知识立意、能力立意”的理念向“价值引领、素养导向、能力为重、知识为基”的理念转变。因此化学平衡常数作为考查学生的知识能力水平的载体，成为了近几年全国各地高考的热门考点。

1.2021年高考化学平衡常数的考查统计

2021年高考已公布的化学学科试卷共有14套，笔者通过分析发现全国各省市的考题中均有对化学平衡常数的考查，其已成为了高考必考点，考查的试题情境也变得愈发新颖多样。具体考查内容统计如表1所示。

2.2021年高考化学平衡常数计算的考查热点

通过表1的考点汇总结果来看，2021年高考化学试题中与平衡常数计算相关的考查形式较为多样。具体考查热点见表2所示。

表2 与平衡常数计算相关的考查热点

表1中数据显示2021年全国各省市高考题中，平衡常数计算共计出现8次，可见化学平衡常数的计算是考查热点之一，且计算的考查形式也在不断地推陈出新。分析其余的考查角度，不难发现其余考查角度的计算问题都是围绕平衡常数进行的，因此平衡常数的计算是解答化学反应原理计算问题的核心，是高考考查的核心知识点。高考试题以“核心价值、学科素养、关键能力、必备知识”为考查内容，以平衡常数知识为载体，利用不同的问题情境，通过增设信息线索涵盖了“四层”中的不同层面，实现对平衡常数知识的考查和对学生综合能力的考查。笔者通过经典试题再现，总结平衡常数计算的有效解题策略，为2022年高考备考提供参考。

3.平衡常数计算的解题策略与典例分析

3.1 单一反应平衡常数的计算

【解题策略】在解决单一可逆反应平衡常数计算问题时，要注意以下几个方面：

①关注体系为恒压体系还是恒容体系，模型如图1所示：

图1 单一平衡下的K的计算解题模型

②关注体系中是否充有不参与反应的气体(如N2或稀有气体等)，在恒压体系中列三段式时可不考虑这类气体，但计算总气体物质的量时要考虑将其加入。

③看清题目要求是写K的表达式(只用物质化学式相关的表示)还是写计算式(只列算式不计算)，又或是书写计算结果，看清题目是只要写数值，还是数值单位均要写。

【典例】

(1)恒压体系

【例1】(2021·湖北省选择性考试·19节选)丙烯是一种重要的化工原料，可以在催化剂作用下，由丙烷直接脱氢或氧化脱氢制备。

(2)对于反应Ⅰ，总压恒定为100 kPa，在密闭容器中通入C3H8和N2的混合气体(N2不参与反应)，在温度为T1时，C3H8的平衡转化率与通入气体中C3H8的物质的量分数的关系如图2所示，计算T1时反应Ⅰ的平衡常数Kp=________kPa(以分压表示，分压=总压×物质的量分数，保留一位小数)。

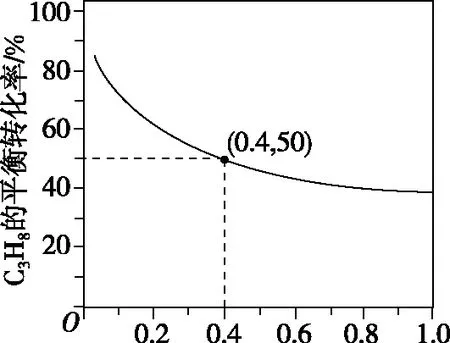
图2

【参考答案及解析】根据图2，C3H8的物质的量分数为0.4时，其平衡转化率为50%。假设混合气体为1 mol，则起始时C3H8为0.4 mol，N2为0.6 mol，运用三段式法计算：

起始量/mol 0.4 0 0

转化量/mol 0.2 0.2 0.2

平衡量/mol 0.2 0.2 0.2

(2)恒容体系

图3

若平衡时体系内压强为p0，b点时反应的平衡常数Kp=________(kPa)-1(以分压表示)

【参考答案及解析】温度不变，则b点和c点的Kp相等，先由差量法求出初始总压为1.2p，再根据图3中信息，c点的n(H2)∶n(CO2)=2∶1，由于该体系为恒容体系，故初始两物质的压强比也是2∶1，则p(H2)=0.8p0，p(CO2)=0.4p0，依据三段式列式计算：

起始量/kPa 0.4p00.8p00 0

转化量/kPa 0.2p00.4p00.2p00.2p0

平衡量/kPa 0.2p00.4p00.2p00.2p0

【误区警示】在例1中学生答题时的常见错误有两个：①计算气体的总物质的量时忘记将N2算入平衡时气体的总物质的量中，导致算出Kp=33.3 kPa。②认为初始时总压为100 kPa，C3H8占40%，则为40 kPa，从而利用压强数据直接代入三段式，计算平衡时各个物质的压强，导致得出错误答案Kp=20 kPa。在例2中常见错误类型是思维固化，认为只要求Kp就想利用三段式求解平衡时各个物质的物质的量分数，进而求分压，忽略了此题是恒容体系，压强是一直在变化的。

3.2 多重平衡常数的计算

【解题策略】遇到多重平衡体系，需厘清多个反应之间的关系，若前一步反应的生成物继续参加第二步反应，这一类反应属于连续型反应。若多步反应之间是平行关系也是相互竞争关系，这一类属于竞争型反应。无论哪一类多重平衡，常用解题方法主要有列三段式法或元素守恒法，其中列三段式法属于解决平衡计算类问题的常规方法，但是针对不同类型的多重平衡反应，列三段式时要合理分析过程，找准突破口。而元素守恒法不考虑中间过程，只注重结果，计算起来更为方便。具体解题模型如图4所示。

图4 多重平衡下K的计算解题模型

(1)连续型

【例3】(2019·天津卷·7节选)在1 L真空密闭容器中加入amol PH4I固体，t℃时发生如下反应：

达平衡时，体系中n(HI)=bmol，n(I2)=cmol，n(H2)=dmol，则t℃时反应①的平衡常数K值为________(用字母表示)。

【参考答案及分析】该反应的体系中有三个连续发生的可逆反应，在平衡体系已知的物质里，只有I2是第③个反应生成的，其余反应都没有I2的参与。因此此题的突破口是I2，并依次确定计算反应①平衡常数所需要的其他物质。

方法一：三段式法

方法二：元素守恒法

只考虑物质的始态和终态，不考虑中间过程，使用元素守恒计算平衡态各物质的物质的量，具体思维如图5所示。

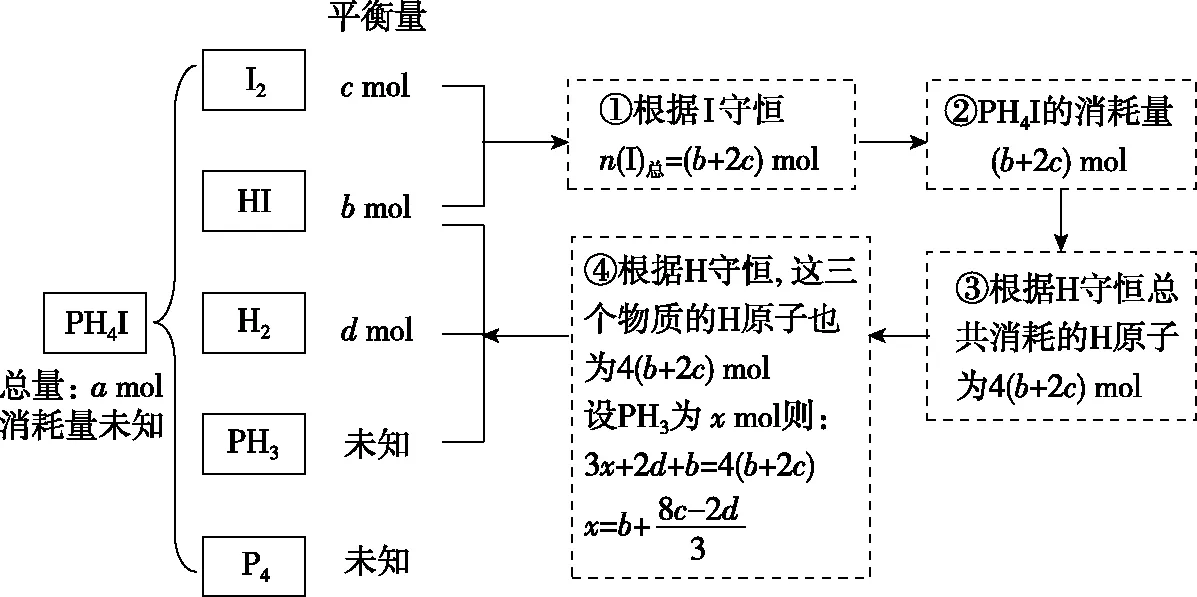
图5 元素守恒法计算思路

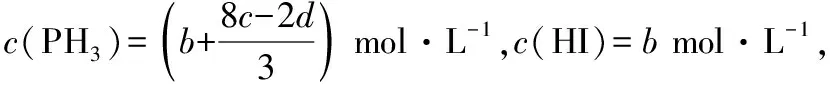
(2)竞争型

【例4】(2020·山东卷·18节选)探究CH3OH合成反应化学平衡的影响因素，有利于提高CH3OH的产率。以CO2、H2为原料合成CH3OH涉及的主要反应如下：

(2)一定条件下，向体积为VL的恒容密闭容器中通入1 mol CO2和3 mol H2发生上述反应，达到平衡时，容器中CH3OH(g)为amol，CO为bmol，反应Ⅲ的平衡常数为________(用含a、b、V的代数式表示)。

【参考答案及分析】方法一：三段式法

对3个竞争反应进行分析，发现反应②+③=①，因此三个反应之间的关系可以用图6表示，可知生成甲醇目标产物的反应可视为主反应，生成CO的反应中未转化为甲醇的反应可视为副反应。

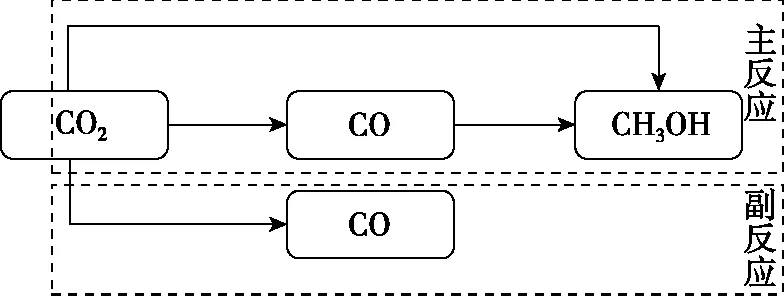
图6 主副反应的分类图示

初始量/mol： 0 0

变化量/mol：a3aaa

平衡量/mol：a

初始量/mol： 0 0

变化量/mol：bbbb

平衡量/mol：b

反应Ⅲ中各气体的物质的量为

方法二：元素守恒法

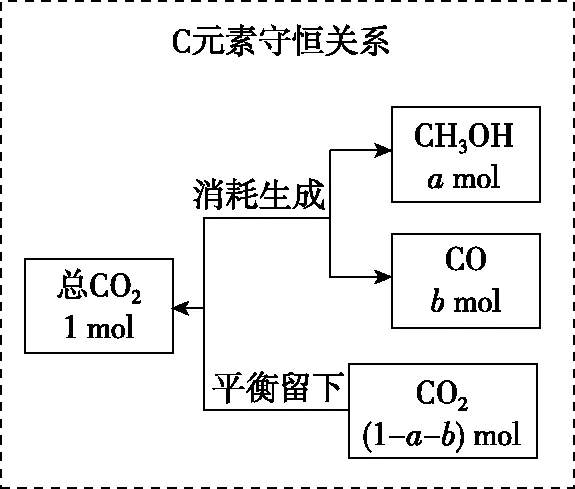
图7 元素守恒法计算思路

【误区警示】学生在计算解决此类多重平衡问题时，容易把平衡浓度带错，注意理解化学平衡常数计算中的浓度均指混合体系中该物质最终达到平衡时的浓度，而不是某一个反应平衡时的浓度。在混合体系中即便所求物质同时参加多个反应，最终的平衡浓度也只有一个。

3.3 新型平衡常数的计算

【解题策略】

(1)辨析不同类型的平衡常数

(2)无论求解何种形式的平衡常数均可以按照以下思路解题：列三段式→利用新概念改变K的表达式→求解。

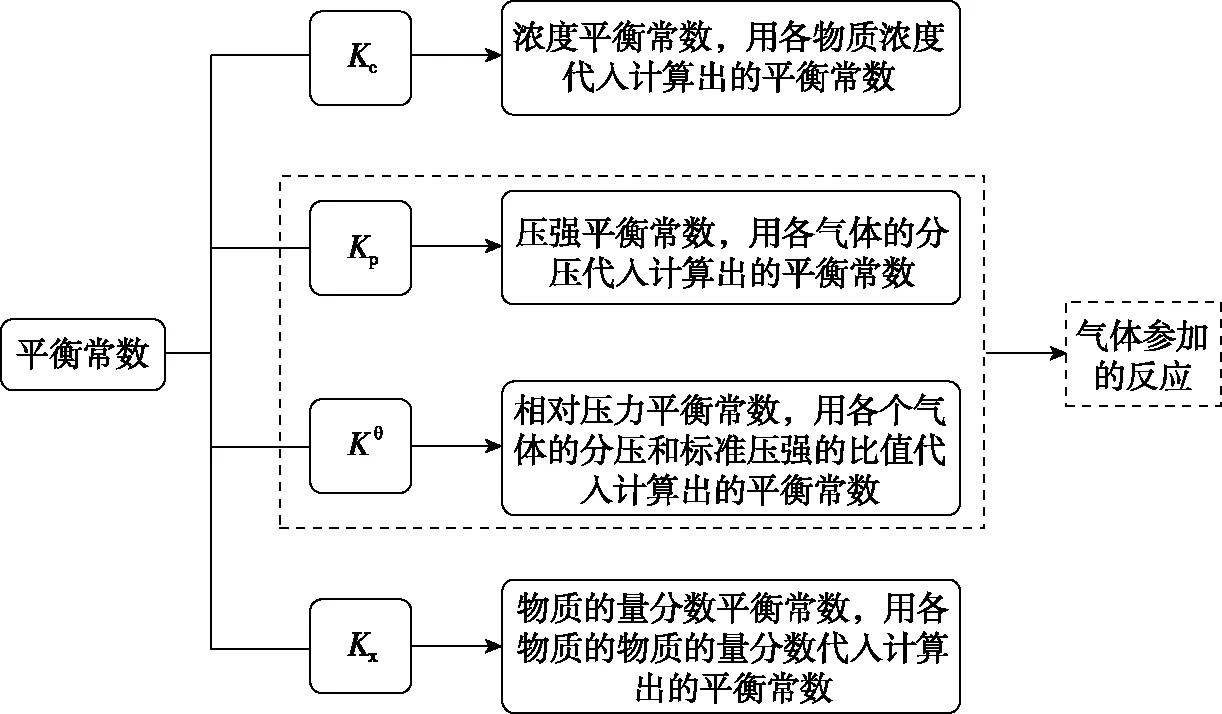
图8 平衡常数的分类

【典例分析】

【例5】(2021·山东省学业水平等级性考试·20节选)2-甲氧基-2-甲基丁烷(TAME)常用作汽油添加剂。在催化剂作用下，可通过甲醇与烯烃的液相反应制得，体系中同时存在如下反应：

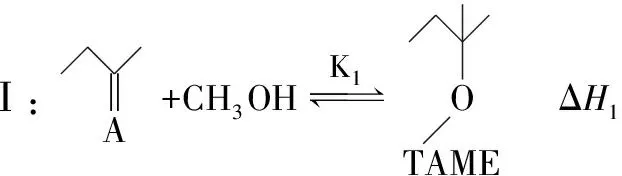
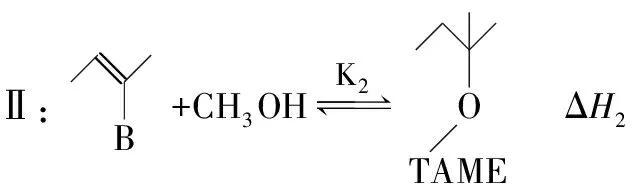
为研究上述反应体系的平衡关系，向某反应容器中加入1.0 mol TAME，控制温度为353 K，测得TAME的平衡转化率为α。已知反应Ⅲ的平衡常数Kx3=9.0，则反应 Ⅰ的平衡常数Kx1=________(Kx是以物质的量分数表示的平衡常数)

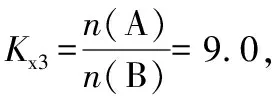
变化量/molxxx

变化量/mol 9x9x9x

TAME共消耗了αmol，则x+9x=αmol，x=0.1αmol，平衡时n(TAME)=(1-α) mol，n(A)=0.1αmol，n(B)=0.9αmol，n(CH3OH)=αmol，一共有气体n(总)=1-α+0.1α+0.9α+α=(1+α) mol

【误区警示】对于新情境下的平衡常数的求解，不要形成思维定式，更不要被试题形式吓得丢盔弃甲。一定要仔细揣摩题目所给的新信息，理解新平衡常数的表示方法，防止出现盲目迁移。

4.复习备考建议

(1)构建概念图，梳理必备知识

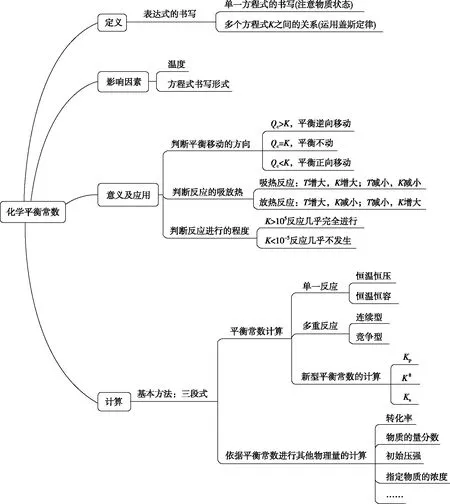
图9 化学平衡常数知识概念图

(2)善于总结，培养关键能力