含石率对断层土石混合体渗流特性的影响

谭文辉，董锋鑫，马学文，王鹏飞

(北京科技大学 土木与资源工程学院，北京 100083)

1 研究背景

突水是矿山开采中常见的动力灾害，据统计，60%矿井事故与地下水作用有关[1]。深部金属矿山中，岩体多为硬岩，质量较好，断层型突水占首位[2]。断层带岩体松散，完整性较差，绝大多数断层裂隙带内均发育有连续且厚度不一的角砾和断层泥混合物，断层带的渗流特性基本上取决于这些土石混合体的渗流特性。研究断层带土石混合体的渗流特性对进一步完善土石混合体力学理论体系和防治断层区工程突水等地质灾害具有重要意义。

对土石混合体强度和渗流特性的研究，目前主要集中在结构要素(含石量、块石形状、孔隙结构、级配等)的影响方面，如金磊等[3-4]、董辉等[5]、周中等[6]、Janssen等[7]、Ring等[8]和罗亦琦[9]研究了砾石含量、孔隙比、颗粒形状和不同级配对土石混合体渗透系数和强度的影响。邱贤德等[10]结合堆石体颗粒的概率统计分布模型，建立了堆石体颗粒含量与渗透系数之间的经验关系式。徐扬等[11]建立了土石混合体颗粒平均粒径、非均匀度与渗透系数的关系。李晶晶等[12]构建了土石混合体的孔隙结构模型，引入格子Boltzmann方法分析土石混合体的渗流特性。

此外，在土石混合体的渗流变形破坏特征方面，徐文杰等[13]研究了土石混合体的细观渗流场特征、渗透破坏机制及宏观渗透系数与细观结构的定量关系。沈辉等[14]采用室内试验与数值模拟相结合的方法，分析了块石含量对土石混合体渗透侵蚀特性的影响，建立了适用于土石混合体的渗流侵蚀模型。胡瑞林等[15]系统阐明了含石量、块石形状、基质组分、土-石级配等关键结构因子对土石混合体强度、变形、渗透特性的影响规律。

上述研究对象主要为土石坝、库岸边坡等地面工程中的土石混合体，针对地下断层破碎带土石混合体渗流特性的研究却鲜有报道。

由构造作用形成的断层破碎带土石混合体具有较高的渗透性，是地下水害的主要通道，因此，本文拟开展断层破碎带土石混合体渗流特性研究。课题组王鹏飞等[16]研究了不施加轴压，只考虑围压和渗压情况下，不同含石率土石混合体试样渗透系数的变化规律，本文拟在其基础上，采用现场取样、实验室重塑的方法，重点研究三轴压力作用下，土石混合体的渗透特性，并采用数值模拟方法从细观上研究不同含石率土石混合体试样的渗流特性和破坏规律，为矿山突水防治提供参考。

2 土石混合体渗流特性试验研究

2.1 试验材料及试样制备

试验所用土石混合体取自三山岛金矿西山分矿高程-780 m水平段北巷F3断层带处，勘探线桩号1820—桩号1840之间，砾石岩性为花岗岩，形状较规则，级配良好，天然含水率约 9.5%。断层破碎带土石混合体充填物的主要成分为具有较强胶结性的绢云母和石英等硅酸盐矿物质，同时还含有少量的高岭石和伊蒙石混层。

土石混合体重塑试样高100 mm、直径50 mm。根据Medley[17]、徐文杰等[18]提出的土石混合体的粒径阈值d=0.05Lc(Lc为土石混合体的工程特征尺度)并参考美国材料与试验协会(ASTM)标准[19]，确定块石的粒径范围为2.5～8.3 mm，<2.5 mm的为土体。

土石混合体的含石率为块石质量与试样总质量的比值，当含石率在20%～70%之间时，由于块石含量和土样含量相对均衡，此时块石含量对土石混合体试样的渗透特性的影响较明显，因此选取含石率分别为20%、30%、40%、50%、60%和70%的6种土石混合体试样，进行不同含石率下断层带土石混合体的渗流特性研究。表1为各含石率土石混合体的粒径分布特征指标。由表1可以看出，含石率为20%的试样均匀性相对较好，其余含石率土石混合体试样均匀性较差。

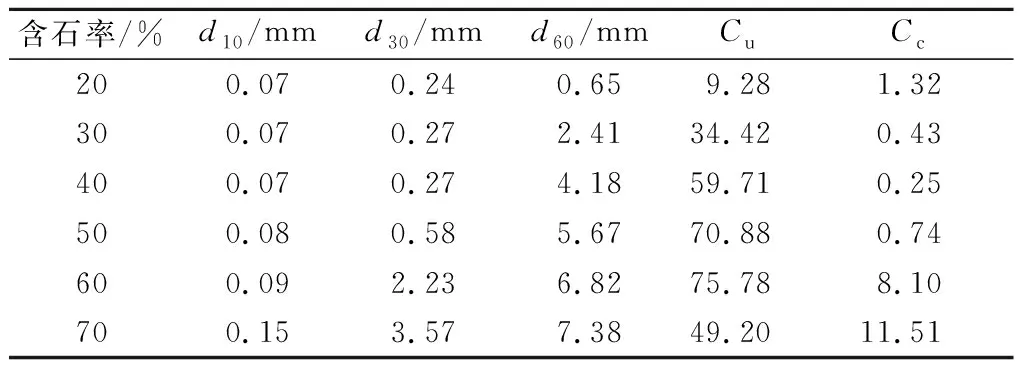
表1 不同含石率土石混合体粒径分布特征指标

为了尽量减少孔隙率与密实度对渗流特性的影响，采用将不同含石率土石混合体试样中的土体调整成统一密度的方法制作试样[16]，根据不同含石率土石混合体中土体的击实曲线确定土体密度定为1.82 g/cm3，通过击实次数控制不同含石率试样中土体的密度。制备试样前，先将模具内部擦拭干净，并涂抹凡士林，按照要进行试验的6种含石率把筛分好的土、石混合拌匀，并加入一定量的水增强其胶结性。将混合好的试样分3层放入模具中，每一层都均匀击实，且击实后对击实面进行刨毛处理。将完成的试件放置到养护箱中24 h后拆模，并继续养护28 d以提高其自由水转化率。制作完成的土石混合体试样如图1所示。本次试验所制得土石混合体试样与断层带土石混合体具有相同的结构成分，但试样尺寸较小且经过压实处理，密实度较大。

2.2 三轴应力状态下的土石混合体渗流试验

矿井深部断层带处的土石混合体由于受到地质构造运动以及水压的作用，一般处于比较密实稳定的状态；但受巷道开挖、爆破扰动等因素的干扰，特别是当巷道穿过断层带时，打破了断层带土石混合体之前所处的平衡状态，导致断层带土石混合体处于应力释放状态。在进行室内试验时，为了更好地契合现场的实际情况，保证试验时土石混合体试样外壁与乳胶套之间不漏水，选取0.10、0.14、0.18 MPa三种围压，研究三轴压力状态下土石混合体的应力、应变及渗透系数的变化情况。

土石混合体渗透试验采用稳态法[20]，应用GDS三轴试验系统进行，将制备好的试样装样完毕后，先对试样施加 0.02 MPa的低水压，直到试样饱和。试验时，渗流水头差保持0.08 MPa不变，即进水口压力设为0.08 MPa，出口通大气，待水压稳定，试样内部达到稳定渗流后正式开始试验。以应力控制方式逐步对土石混合体试样施加轴向荷载，记录每级轴压下的渗流量并计算渗透系数。为保证试验结果的精确性，土石混合体的应变控制在12%以内。

根据达西定律，土石混合体试样渗透系数k的计算公式为

(1)

式中：γw为水的重度(kN/m3)；Q为单位时间通过试样的水量(m3/s)；L为试样高度(m)；A为试样截面积(m2)；Δh为试样两端水压差(MPa)。

2.2.1 不同围压下土石混合体试样应力-应变与渗透系数-应变的变化规律

图2是不同围压下土石混合体试样应力-应变-渗透系数的变化情况，由图2可以看出：

(1)随着围压和含石率的提高，土石混合体试样的强度均呈现增大的趋势。

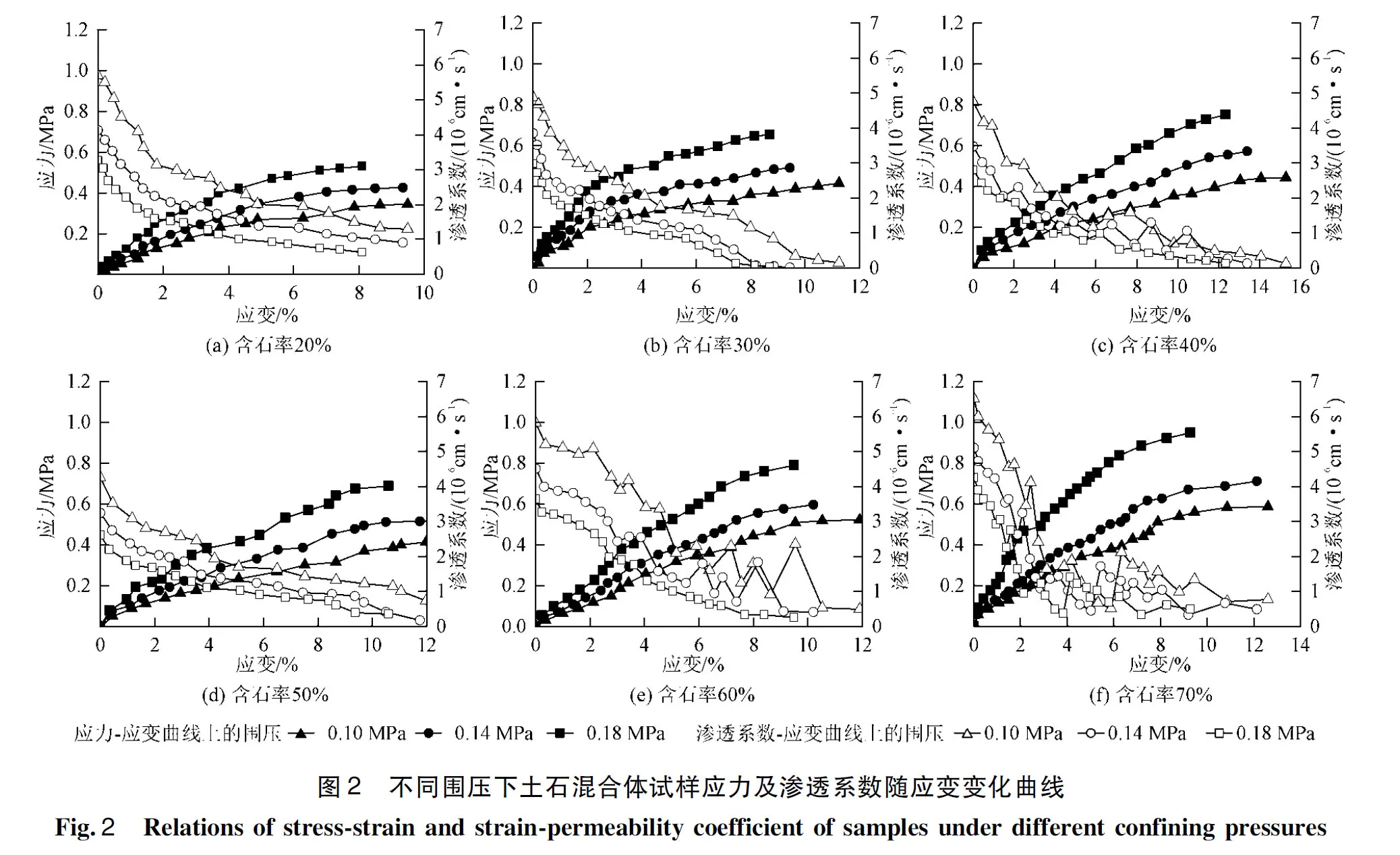
(2)不同含石率条件下，试样渗透系数均随围压的增大而减小，同时，随着变形的增大，渗透系数总体上也逐渐减小。当含石率在20%～40%时，随着应变的增加，渗透系数的变化曲线是单调的，而含石率>50%时，渗透系数出现了一定的波动。造成这种现象的原因是当含石率较高时，块石在试样中占据主导地位，在压缩过程中块石容易发生位移，易出现短暂的较大孔隙，导致渗透系数发生突变。

(3)随着压力的增加，不同含石率试样的渗透系数变化范围并不大，没有数量级的变化，这是由于为了尽量减少孔隙率与密实度对渗流特性的影响，试验前土石混合体试样经过击实压密处理，试样内部大部分孔隙被压缩，使压力变化对渗透系数的影响有所减小。

土石混合体试样在无轴向压力[16]和三轴应力状态下的渗透性存在一定的联系和区别。在同一含石率下，两种应力状态下土石混合体试样的渗透性都是随着围压的升高而降低；含石率的高低对试样的渗透性具有较大的影响，40%含石率在两种应力状态下都相对特殊。区别在于无轴向压力时，试样的渗透系数变化曲线是比较光滑的；三轴应力状态下，当含石率在50%～79%之间时，渗透系数变化曲线出现一定的波动。

2.2.2 土石混合体试样渗透系数与轴压函数关系

在三轴应力状态下，除了围压对土石混合体试样渗透性的影响外，轴向压力的变化同样是影响试样渗透系数变化的重要因素。土石混合体试样渗透系数与轴压的关系可通过非线性拟合，其指数函数关系式为

k=k0exp(-aσ) 。

(2)

式中：k为土石混合体试样的渗透系数(cm/s)；k0为初始渗透系数(cm/s)；a为拟合参数；σ为轴压(MPa)。

不同围压下，不同含石率土石混合体试样的渗透系数与轴压关系拟合曲线及拟合结果分别如图3和表2所示。曲线整体拟合效果较好，拟合度均在90%之上。其中含石率为20%、40%时的拟合效果最好，在三种围压条件下拟合度均在95%之上；含石率为70%时的拟合效果稍差，但拟合度也在90%以上。式(2)较好地描述了土石混合体试样渗透系数与轴压的指数函数关系。由图3可以看出，随轴压的增大，不同含石率下的试样渗透系数均有所下降。同一应力状态下，随着含石率的增加，试验渗透系数先减小后增大，含石率40%时达到最低，之后迅速升高，且随轴压增大，不同含石率试样的渗透系数差距逐渐减小，这与先前未施加轴压下的渗流试验结果[16]一致。由表2也可以看出，围压越大，初始渗透系数越小，这是因为试样在围压作用下密实度较高，空隙率低。

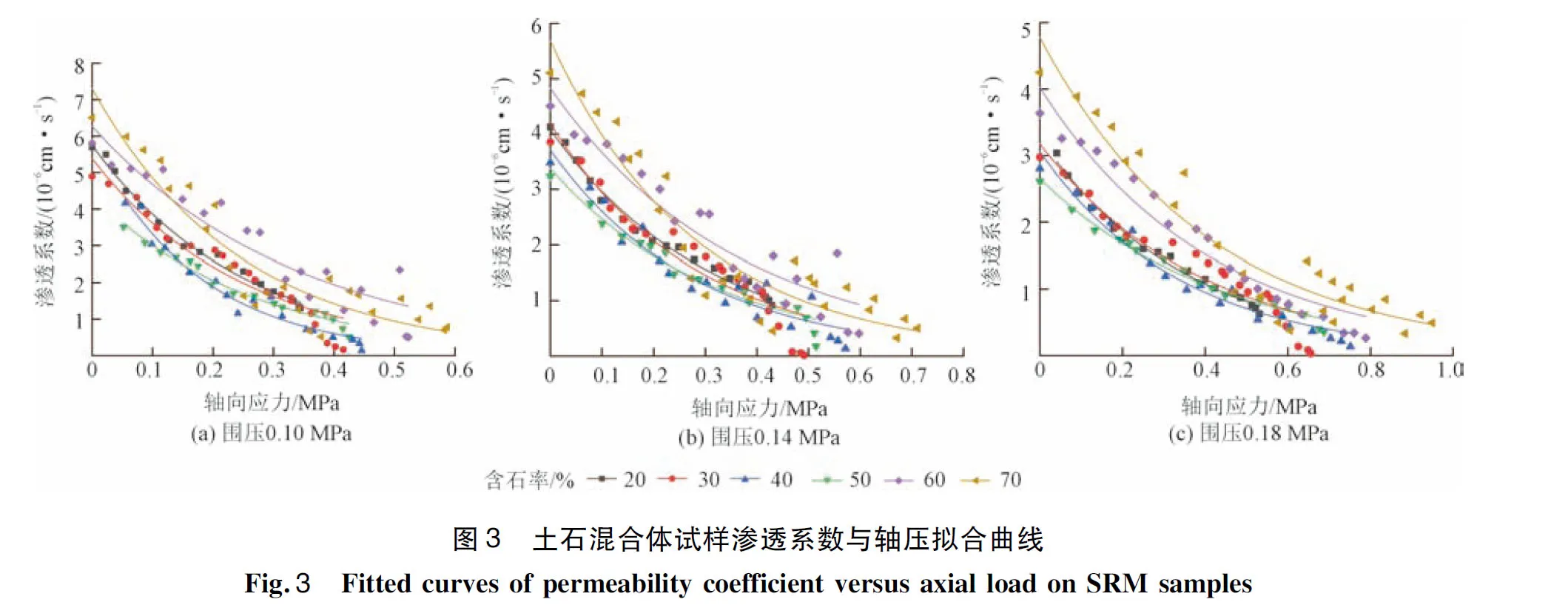
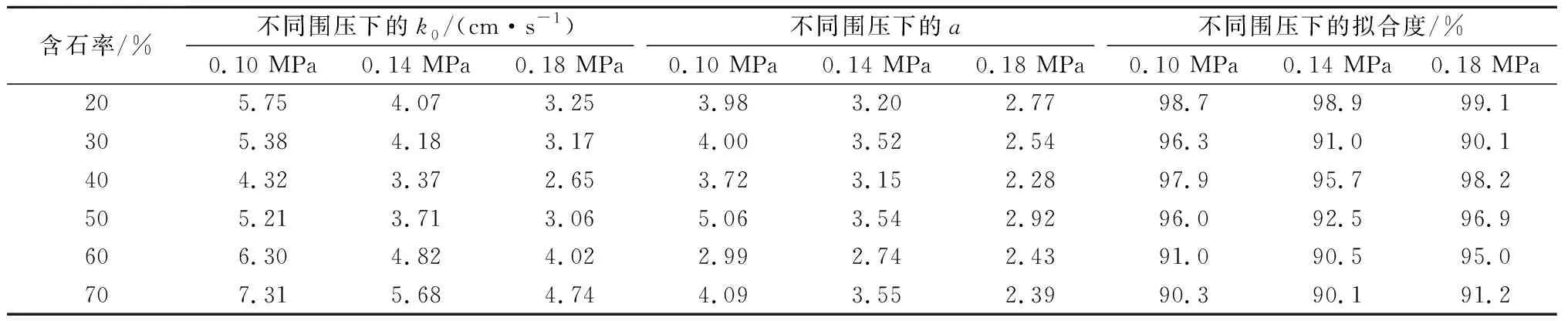
表2 土石混合体试样渗透系数与轴压指数函数拟合结果

2.2.3 渗透系数对含石率变化的敏感性分析

将土石混合体渗透系数对含石率变化的敏感系数ck定义为[16]

(3)

式中：Δk为土石混合体试样的渗透系数差值(cm/s)；k20为含石率为20%时的渗透系数(cm/s)；ΔRc为不同含石率与20%的差值。

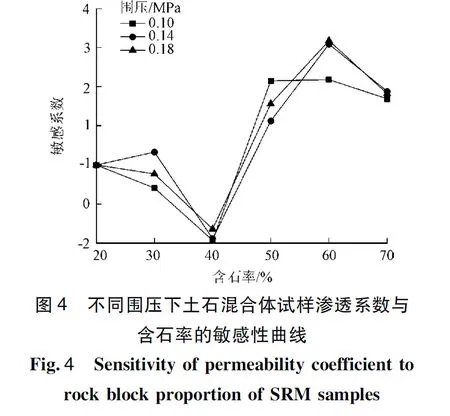
图4反映出3种围压下土石混合体渗透系数对含石率变化的敏感性。 由图4可以看出：含石率较小时，土石混合体试样渗透系数对含石率变化的敏感系数较小，且以负向敏感为主，敏感系数<0，随着含石率的升高，敏感系数逐渐由负向敏感变为正向敏感。在含石率为40%时，敏感系数接近-2，说明渗透系数变化较大；含石率>40%后，试样中块石逐渐处于主导地位，含石率的微小变化就可能引起试样孔隙度的巨大改变，因此试样渗透系数对含石率的敏感度不断增大，到60%时达到峰值，敏感系数>3，而且围压越大，敏感系数越大；含石率>60%后，块石处于土石混合体试样中的主导地位，其含量变化对试样孔隙度的影响已十分有限，敏感系数又开始降低。总体而言，敏感系数的绝对值越大越敏感，含石率40%和60%分别是曲线上负向和正向的最敏感点。

3 土石混合体渗流特性数值模拟

为了研究土石混合体在水压作用下内部水渗流以及破坏演化情况，采用岩石破裂过程分析(Rock Failure Process Analysis，RFPA)软件进行模拟研究。RFPA 数值模拟软件可以模拟裂纹的萌生、扩展等岩体破坏过程，其中的RFPA2D-Flow 固液耦合模块可以较好地模拟岩石、土体等固体材料的渗流破坏过程问题[21-22]。

3.1 模型的建立

建立如图5所示的3种含石率试件的二维平面模型，模型高100 mm，宽50 mm，考虑块体的最小值与最大值，取5 mm为模型中石块直径，随机分布。模型中土和岩石的各项参数见表3。模拟分析过程中，取侧压为实验中的中间值0.14 MPa，对模型施加0.1 MPa下进水口水压和0.02 MPa上出水口水压，加载过程采用位移控制，位移增量ΔS=0.03 mm，即每步0.03 mm，加载步数设置为80步，模型中的块石渗透系数极低，可以看成几乎不渗水。

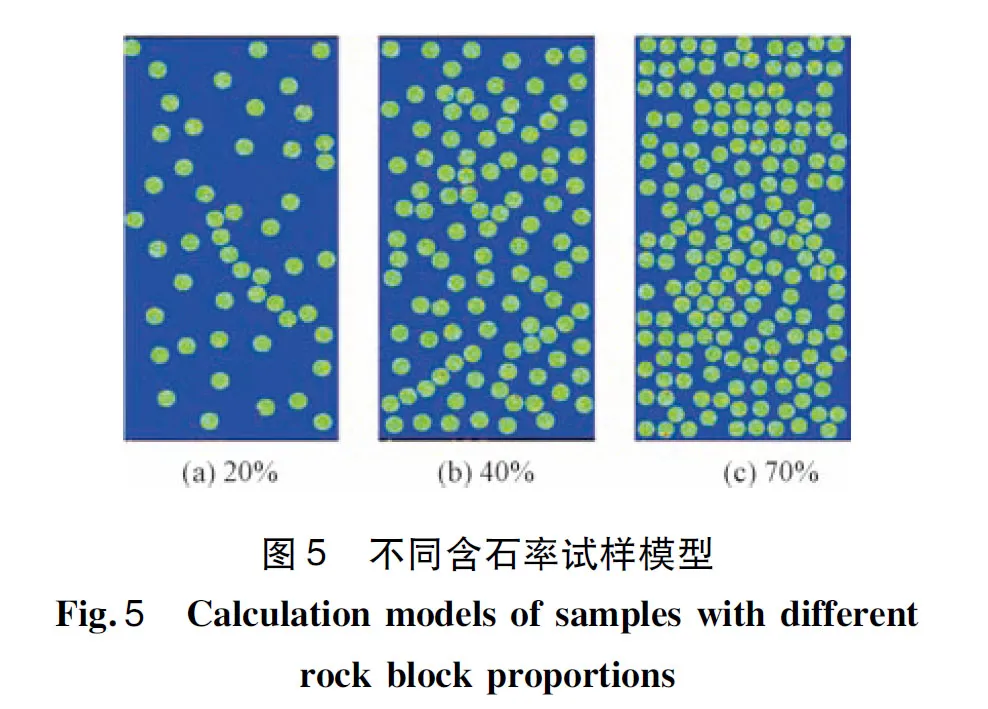
表3 土和岩石的物理力学参数

3.2 数值模拟结果分析

3.2.1 孔隙水压力条件下含石率对土石混合体强度的影响

图6是孔隙水压作用下，土石混合体强度的变化曲线。由图6可见，在孔隙水压力条件下，整个应力应变过程可分为：线弹性阶段、非线性变形阶段及软化阶段。 20%、40%、70%含石率模型的峰值强度分别为1.14、1.22和1.47 MPa，可见含石率越大，试样的强度越大。

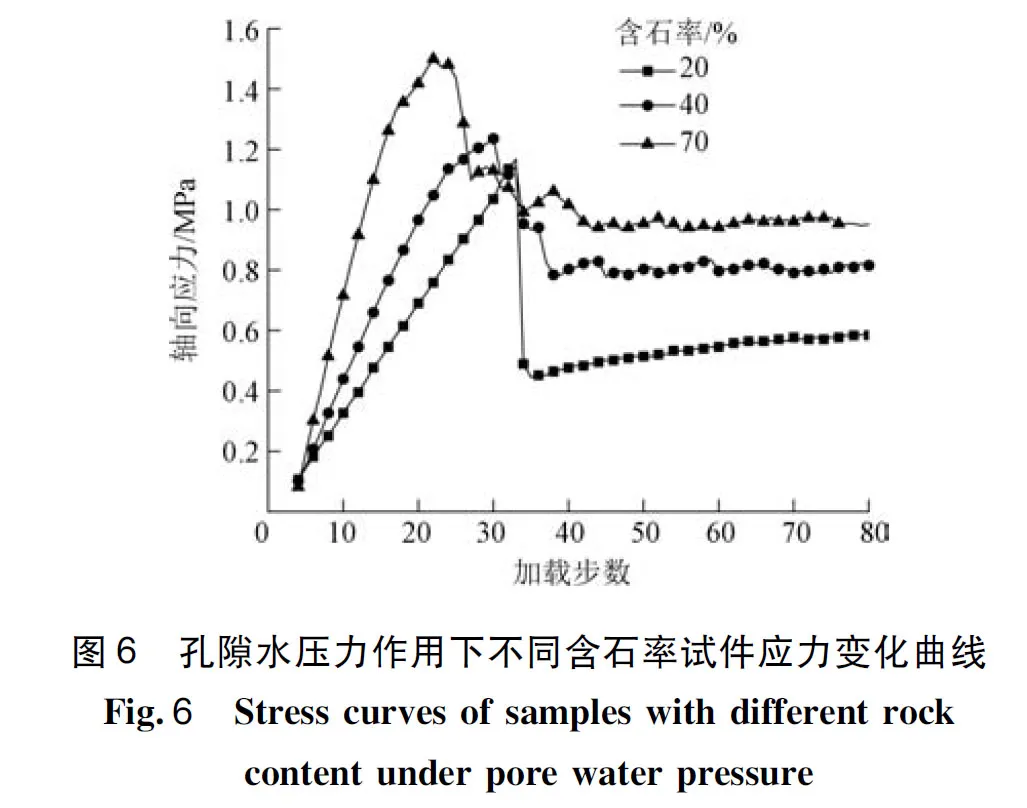
不同含石率下的土石混合体数值模型到达峰值强度的加载步数也是不一样的，20%、40%及70%含石率试样到达峰值强度的加载步数分别为35、30、22，这是因为土样的含量较高时，试样可被压缩的空间较大，需要的加载步数相对多一些，而当块石的含量较高时，试样被压缩的空间减小，试样到达峰值强度的加载步数要少。当含石率较低时，试样模型的应力变化曲线较为光滑，而随着含石率的增加，模型在非线性变形阶段以及软化阶段时应力曲线有一定的起伏。

3.2.2 土石混合体破裂过程中渗透系数的变化

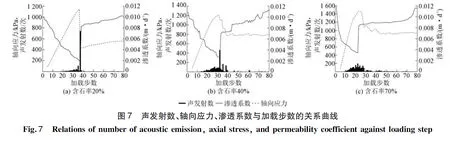
为了研究土石混合体试样破裂特性，将试样加载过程中的渗透系数、轴向应力及声发射情况绘制在同一个坐标图中，如图7所示。由图7可见：

(1) 在初始阶段，随着时步增加，土石混合体试样逐渐密实，渗透系数逐渐减小。继续加载，试样的密实度进一步增加，渗透系数变化趋势减缓。当土石混合体试样的强度达到峰值时，试样被压缩到最密实状态，含石率20%、40%和70%所对应的渗透系数分别为0.002 8、0.002 2、0.003 4 m/d。上述3种试样中，含石率40%的试样渗透系数最低，含石率70%试样的渗透系数最高，这与试验结果一致。当继续加载到试样发生破坏时，试样出现了贯通裂纹，由于围压的作用，此阶段试样渗透系数的增加比较缓慢。

(2) 当试样达到峰值强度时，声发射数最高，含石率20%、40%和70%所对应的峰值强度声发射数分别为742、464和193。可见，含石率越高，到达峰值强度时的声发射数越低。土石混合体试样的破坏与声发射能量变化具有对应关系，而且随着含石率的升高，试样破坏失稳时的声发射次数也越低。渗透系数的突变发生在试样破裂之后，二者之间具有一定的时间差。

3.2.3 不同含石率下土石混合体的破裂模式

图8显示了不同含石率试件在加载过程中3个时间点的裂纹出现与声发射情况。从图中可以看出：

(1)试样在线弹性阶段均未出现裂纹，当含石率为20%，加载到35时步，模型到达破裂临界点，但裂纹变化并不明显，当继续加载到70时步，可以看到有一条较为明显的裂纹沿着块石排列较为集中的方向展开。

(2)当含石率为40%，加载到第30时步，模型到达破裂临界点，已经可以看出有多条细微的裂纹；继续加载到第70时步，清晰可见多条裂纹，其中最为明显的裂纹出现在模型中间块石分布较为松散处。

(3)当含石率为70%，加载到第22时步，模型到达破裂临界点，沿着块石之间的缝隙出现了多条裂纹；继续加载到第70时步，试样出现了非常明显的破坏。

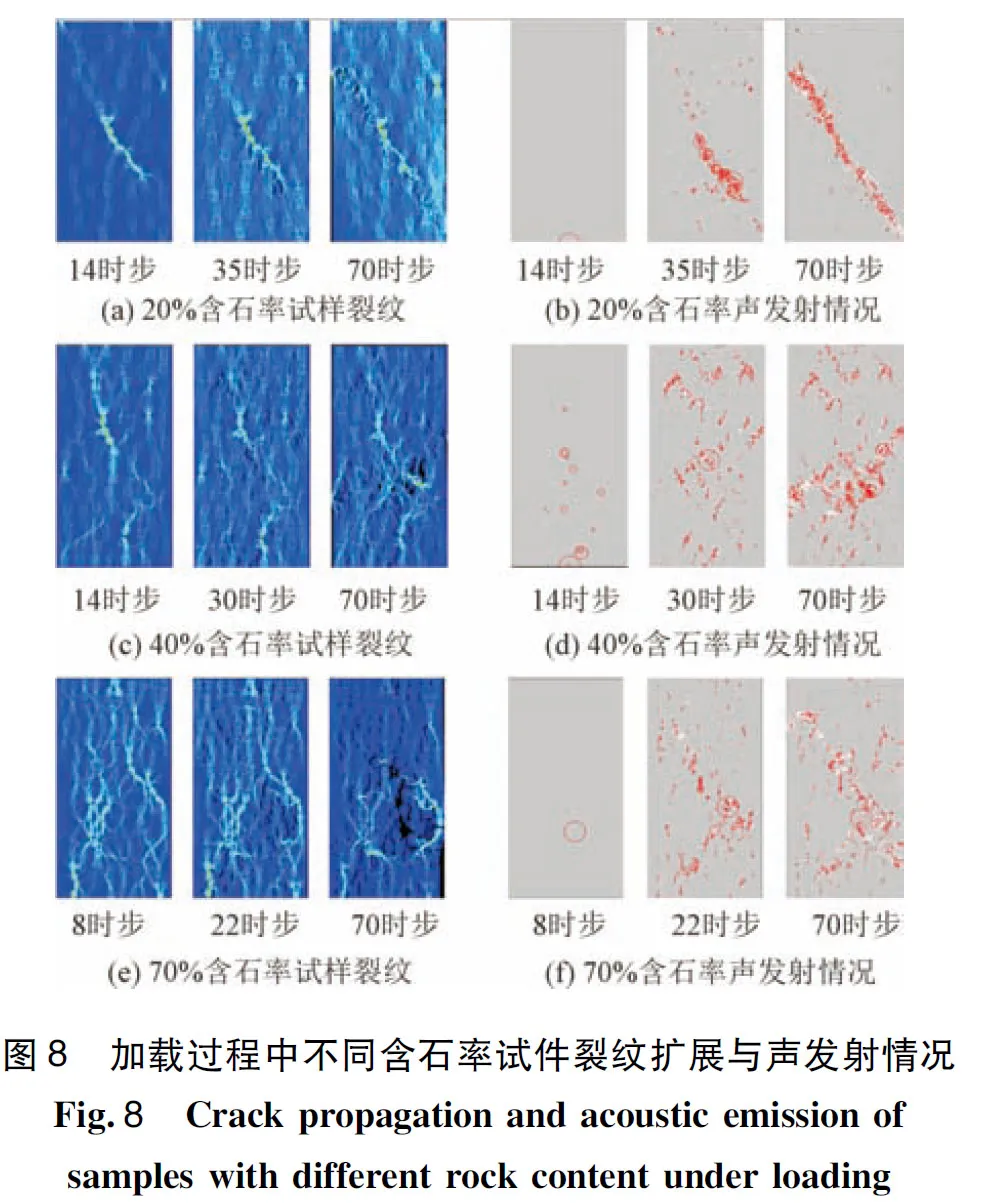
从土石混合体试样各阶段的声发射情况也可以直观地看出试样在加载过程中的破裂情况。含石率为20%时，试样的声发射能量区主要是在块石集中的边缘区；当含石率为40%和70%时，声发射能量区主要集中在块石与块石之间的填充土样区，声发射能量集中的区域正是试样出现裂纹的区域。

4 结 论

土石混合体是断层破碎带的重要组成部分，为研究其渗流特性，本文采用现场取样、实验室重塑的方法开展了不同含石率的土石混合体GDS三轴渗流试验，并利用RFPA模拟分析了不同含石率下的土石混合体渗流特性和破坏演化规律，得到以下结论：

(1)对含石率为20%、30%、40%、50%、60%、70%的土石混合体重塑试样的GDS三轴渗流试验发现，40%含石率是试样渗透系数变化曲线的转折点；同种含石率下围压和轴压的增加都会引起试样渗透系数的下降；渗透系数与轴压间的关系可用指数函数描述。

(2)采用RFPA软件对20%、40%、70%含石率的土石混合体模型进行了渗流的数值模拟试验。分析得出，在孔隙水压力一定情况下，含石率越高，土石混合体强度也越高；加载过程中土石混合体的裂纹集中出现在块石与块石之间的填充土样处；渗透系数的突变点与试样峰值破坏强度点及声发射次数最高点一致。

(3)由于数值分析模型采用二维平面应力模型，对模型施加侧压，轴向加载试验时可以加载到破坏，因此可以看到渗透系数出现突变，而GDS试验是在三维应力状态下，对土石混合体试样施加围压，且设定应变不超过12%，所以两种情况下的试验结果不是定量对应的，但是两种方法得出的渗流规律较为吻合。

(4)由于本文采用的是重塑试样，其结构与自然状态有所改变，因此研究成果与断层带土石混合体实际渗流情况会有一定的差别。但是含石率对土石混合体的渗透系数、渗流路径、渗流破坏的影响仍然可以为实际工程提供参考。