嵌入差分进化和惯性权重的正弦余弦算法*

宁中正,和 煦,杨小勇,赵小强

(1.西安邮电大学 通信与信息工程学院，陕西 西安 710121； 2.国家无线电频谱管理研究所，陕西 西安 710061)

0 引 言

在图像处理、生产调度、特征集选取等工程领域中，绝大多数的工程应用问题都可以转化为最优化问题，而群体智能优化算法能使一些用常规优化算法难以解决的复杂问题得到解决，因此,各类性能优异的群体智能优化算法成为当前一个热点研究方向。其中较经典的优化算法主要有遗传算法(genetic algorithm,GA)[1]、差分进化(differential evolution,DE)算法[2]、粒子群优化(particle swarm optimization,PSO)算法[3]等。随着人们对新优化理论和算法的需求增多，近些年也相继出现了新的优化算法，如果蝇优化算法(fruit fly optimization algorithm,FOA)[4]、灰狼优化(grey wolf optimizer,GWO)算法[5]、鲸鱼优化算法(whale optimization algorithm,WOA)[6]等。

然而几乎不存在一个算法能有效解决所有的优化问题，这激励着国内外学者不断尝试新的思路来开发新的算法。基于这一思想，Mirjalili S于2016年提出了正弦余弦算法(sine cosine algorithm,SCA)，其在飞机的翼型设计[7]，电力系统[8]，图像分割[9]等方面取得了较好的应用效果，充分证实了SCA解决优化问题方面的显著优点。然而该算法也存在易陷入局部最优和收敛速度较慢等问题。

近几年，国内外研究学者通过引入不同的策略，基于SCA提出了不同的改进方法。文献[10]引入动态惯性权重、指数型递减函数以及变异因子，提出一种多策略改进的SCA，提高了算法的收敛速度及精度。文献[11]设计转换参数抛物线函数递减和指数函数递减的两种策略，平衡了局部开发和全局搜索能力。文献[12]引入反向学习策略，提出一种基于反向学习的SCA，提高了种群的多样性。文献[13]引入精英反向学习和个体的反思学习策略，提出一种具有学习机制的SCA，提高了算法的全局优化能力。文献[14]提出一种基于对数非线性参数调整和精英混沌搜索策略的交替SCA，提升了算法的全局搜索与局部开发能力。尽管以上研究使SCA在寻优精度上有一定的提高，但由于该算法较新颖，对其研究还需进一步加强。

本文针对原始SCA的不足，通过引入动态变异因子对DE算法进行改进，然后将这种动态变异的DE嵌入到SCA中，改善SCA易陷入局部最优的缺点。同时通过个体的适应度值引入自适应惯性权重，提出一种改进的SCA(improved SCA,ISCA)。并与原始的SCA,DE以及PSO算法比较，通过实验表明ISCA显著的性能优势。

1 SCA

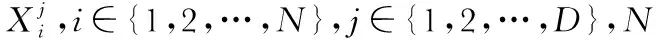
(1)

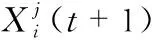
(2)

式中a一般取值为2；t为当前的迭代次数；T为算法的最大迭代次数。

最后计算更新后种群中所有个体的适应度值，选出当前迭代的最优位置和对应的最优适应度值。通过不断增加迭代次数来更新个体位置，直至满足终止条件跳出循环，输出当前最优解。

与其他智能优化算法相比，SCA在求解优化问题的全局最优解方面存在一定的优势：其参数少，结构简单，易实现，能求解不同领域的优化问题，如很好解决了优化飞机的翼型设计问题。同时也存在一些不足：在部分测试函数上易陷入局部最优，寻优精度有待提高；由于惯性权重一直默认为1，在迭代后期上一代个体的位置信息易使得当前个体发生位置震荡。

2 ISCA

2.1 嵌入动态变异的差分进化

针对原始SCA在部分测试函数上易陷入局部最优的问题，嵌入全局搜索能力较强的动态变异DE算法，该算法主要包括如下操作步骤:

1)变异操作，标准DE算法中变异操作的变异因子F的值为常数，其值越大全局搜索能力就越强，本文采用动态的变异因子F，使得F随着迭代次数的增加而减小，前期保持较强的全局搜索能力，后期保持较强的局部开发能力，变异因子F和变异操作的表达式分别为

F=0.4×[cos((t-1)π/T)+Fmax]+Fmin

(3)

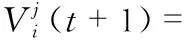
i≠k1≠k2≠k3

(4)

2)交叉操作，通过交叉概率决定个体的交叉情况，交叉操作表示为

(5)

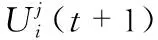
3)选择操作，采用贪婪策略从当前目标个体和经过变异、交叉操作之后的实验个体之间选择适应度值更优者。

从以上三个操作步骤可以看出DE算法采用变异和交叉操作，通过增加种群的多样性来提高全局搜索能力。采用贪婪策略选择较优的个体作为下一次迭代个体，增强算法收敛到全局最优的能力。而从式(1)可以看出，在SCA中个体的搜索机制与DE算法不同，主要依赖上一次个体位置及当前最优位置来进行自身位置的更新，导致算法有可能陷入局部最优。因此，将动态变异的DE算法嵌入到SCA中，有利于加强SCA的全局搜索能力，改善其易陷入局部最优的缺点。

主要思想是将动态变异的DE嵌入到SCA的位置迭代之后，通过交叉、变异操作之后分别计算当前个体的适应度值与之前仅执行SCA个体的适应度值，并作比较进行择优选择，只有适应度较优的个体才被选为下一次迭代的个体，否则继续选用仅执行SCA的个体。

2.2 引入自适应惯性权重

在SCA迭代寻优的过程中，应用较多的是随着时间线性减小的惯性权重，经过测试发现，在部分单峰函数上有较好的性能提升，但在其他函数上性能表现较差。为了弥补这一不足，本文在嵌入了动态变异的DE基础上，提出一种自适应的惯性权重方法。此惯性权重表示为

(6)

式中wmax和wmin分别为惯性权重的最大值和最小值；t为当前的迭代次数；T为算法的最大迭代次数；fi(t)为第i个个体在第t次迭代时的适应度值；favg(t)和fbest(t)分别为第t次迭代时所有个体的适应度平均值和最优值。

通过个体的适应度值对权重进行动态调整，当个体的适应度值小于或等于适应度平均值时，主要依据与适应度最优值的差值来调整惯性权重。其中当差值较小时，说明个体离最优解较近，此时应减小惯性权重，增强局部开发能力。当差值较大时，说明个体离最优解较远，此时应增大惯性权重，增强全局搜索能力。当个体的适应度值大于适应度平均值时，说明个体离最优解更远，此时直接赋值为最大惯性权重，使个体保持较强的全局搜索能力。因此，算法的位置更新方程由式(1)变换为如下

(7)

2.3 一种嵌入差分进化和惯性权重的ISCA

ISCA主要针对原始SCA易陷入局部最优的不足，嵌入动态变异的差分进化算法来增强全局搜索能力，同时引入自适应惯性权重来平衡全局搜索和局部开发能力，减少算法陷入局部最优的概率。ISCA的主要步骤如下：

Step1 初始化种群规模、种群维度、最大迭代次数等各参数，并随机产生初始种群；

Step2 计算初始种群中所有个体的适应度值，并记录当前最优个体；

Step3 更新r1,r2,r3,r4，并依据式(6)更新惯性权重；

Step4 每个个体依据式(7)进行位置的更新；

Step5 依据式(3)更新变异因子，并执行变异、交叉以及选择操作；

Step6 计算种群中所有个体的适应度值，并更新最优个体及最优适应度值；

Step7 若达到最大迭代次数，则算法结束，输出最优适应度值和最优个体，否则返回Step3继续执行。

时间复杂度可以间接反映算法的运行效率，在原始SCA中时间复杂度主要受算法的最大迭代次数T，种群规模N以及空间维度的D影响，SCA的时间复杂度为O(T(N×D))。由以上步骤可以看出ISCA较原始SCA主要增加了引入自适应惯性权重和动态变异的差分进化算法步骤，其中引入自适应惯性权重增加了O((T×N))的计算量，引入动态变异的差分进化算法增加了O(T(N×D))的计算量，因此,整个ISCA的时间复杂度为O(2×T(N×D)+O(T×N)，高于SCA的时间复杂度。但当优化问题的空间维度较高时，ISCA的时间复杂度近似为O(T(N×D))，与原始SCA的时间复杂度一致。

3 算法设计与仿真

3.1 参数选取

种群规模都设置为30，最大迭代次数都设置为1 000，ISCA的wmax和wmin分别设置为1.1和0.1，Fmax和Fmin分别设置为1.0和0.1，CR设置为0.2；DE算法的变异因子F和CR依据文献[15]分别设置为0.5和0.2；PSO算法的各参数依据文献[14]进行设置，其中,vmax和vmin分别设置为6和-6，wmax和wmin分别设置为0.9和0.2，c1和c2都设置为1.496。

3.2 算法仿真

本文中所有的算法均采用MATLAB 8.5软件编程，在Intel®CoreTMi7 CPU，8 GB内存，2.6 GHz主频的计算机上实现。采用表1中9个测试函数对SCA,DE,PSO和ISCA四种算法的性能进行对比测试。其中f1～f5为单峰函数，f6～f9为多峰函数，除了f6函数的理论最优值为-12 569.5外，其余函数的理论最优值都为0。为了避免单次测试的误差，将测试函数在每个算法上独立运行40次，分别记录其平均值和标准差。统计结果如表2所示，较好的优化结果用粗体表示。同时选取其中4个函数的收敛曲线进行展示，如图1所示。

图1 部分函数在SCA,DE,PSO及ISCA算法上的收敛曲线

表1 测试函数的基本信息

表2 测试函数在4种算法上独立运行40次的结果对比

3.3 ISCA算法分析

从ISCA的设计角度分析，在SCA的基础上嵌入动态变异的DE算法，增强全局搜索能力，同时根据个体的适应度值引入自适应惯性权重来平衡全局搜索和局部开发能力，使得ISCA较原始的SCA有显著的性能优势。

ISCA在表1中所有单峰函数上的平均值和标准差均优于对比的3种算法，且在f1～f3函数上都收敛到了理论最优值。说明ISCA在单峰函数上具有较好的寻优精度和稳定性；同时，ISCA在表1中所有多峰函数上，除了在f6函数上的平均值差于DE和PSO算法外，其余测试结果均优于对比的3种算法，其中在f7和f9函数上都收敛到理论最优值，说明ISCA在大多数多峰函数上同样具有较好的寻优精度和稳定性。

3.4 工程应用

将本文提出的ISCA应用于一个经典的工程优化问题，即压力弹簧设计，设计图如图2所示。

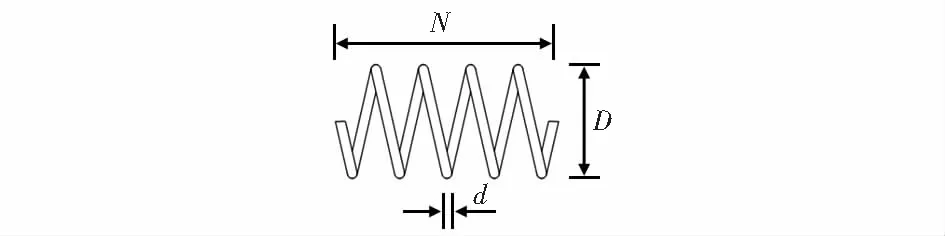
图2 压力弹簧设计

压力弹簧设计旨在求解弹簧重量的最小值，有3个变量分别为线的直径d，平均线圈直径D，有效线圈数量N，令x=[x1,x2,x3]=[d,D,N]，其中x1,x2,x3的取值范围分别为[0.05,2]，[0.25,1.3],[2,15]将此优化问题描述为如下

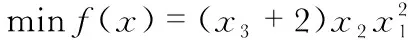
(8)

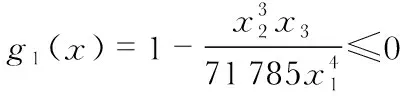
(9)

(10)

(11)

(12)

依据文献[16]中的惩罚函数设计方法,将约束优化问题转化为无约束优化问题，算法的种群规模设置为30，最大迭代次数设置为1 000，分别独立运行20次，记录各参数的平均值，结果如表3所示。

表3 压力弹簧设计问题的对比结果

可以看出，ISCA较DE和PSO算法，能寻求较好的优化效果。说明ISCA在求解较复杂的非线性约束优化问题时具有一定的性能优势。

4 结束语

通过在原始的SCA中嵌入动态变异的差分进化算法，来增强全局搜索能力，并根据个体的适应度值引入自适应惯性权重来平衡全局搜索和局部开发的能力，使得本文提出的ISCA在测试函数上具有较好的寻优精度和稳定性，且在部分测试函数上都收敛到了理论最优值。最后将其应用于压力弹簧设计的优化问题，结果也表明ISCA的性能优势。基于这些优势，有望应用于无线传感器网络分簇路由算法的研究中。