三维环境中机器人路径规划方法研究*

任鑫磊,徐坚磊,陈海辉,张 行,胡燕海

(1.宁波大学 机械工程与力学学院,浙江 宁波 315211; 2.宁波航工智能装备有限公司,浙江 宁波 315311)

0 引 言

随着智能制造时代的到来,智能化与每个人的生活息息相关。类似于扫地机器人等服务型机器人,工作在未知环境时,首先需要规划一条从起始点到目标点的连续的安全无碰撞的最佳路径[1]。

针对这一问题,国内外大量学者展开研究,提出了诸多路径规划算法,如A-Start算法[2]、D-Start算法[3]等,以及众多的群智能优化仿生算法,如蚁群优化(ant colony optimization,ACO)算法[4,5]、人工鱼群算法(artificial fish swarms algorithm,AFSA)[6]、灰狼算法(grey wolf algorithm,GWA)[7]、遗传算法(genetic algorithm,GA)[8]、传统人工蜂群(artificial bee colony,ABC)算法[9]等。这些算法应用于求解二维路径规划问题,表现出较好的规划效果。其中,ABC算法因不需要了解问题的特殊信息,只需要对问题进行优劣的比较,通过各人工蜂个体的局部寻优行为最终求解出全局最优值,有着较快的收敛速度,并且其操作简单、易于实现、控制参数少,故应用尤为广泛[10]。但通过实验发现将ABC算法应用于求解三维未知环境中规划路径问题时,求解精度、程序完整运行时间等有待提高。

因此,针对解决三维未知环境中路径规划问题,本文基于ABC算法,引入正态分布理论优化蜜源初始化分布,构建蜜源中心领域范围内求解新蜜源的数学模型,提出基于改进人工蜂群算法(improved ABC,IABC)的路径规划方法,最后应用MATLAB曲面网格划分建立三维未知环境模型,求解从初始点到目标点的最优路径,并通过实验验证本文提出方法的有效性。

1 传统ABC算法

Karaboga在2005年为解决多变量函数优化问题,提出传统人工蜂群算法模型[11]。在自然界中蜜蜂是一种群居性昆虫,在任何环境下总以极高的效率找到优质蜜源,且能适应环境的改变[12]。这一特性为应用ABC算法求解路径规划问题提供了思路。

ABC算法求解三维未知环境路径优化问题的过程,通过蜜蜂采蜜行为实现。蜜蜂群的采蜜系统主要由蜜源、采蜜蜂、跟随蜂、侦察蜂等组成。其中,蜜源为待优化路径可行解；采蜜蜂采用贪婪准则,比较记忆中的最优路径和领域搜索解,当搜索解优于记忆最优路径时,替换记忆解,反之,保持不变；跟随蜂则根据采蜜蜂提供的蜜源信息以一定概率选择蜜源；等某处蜜源陷入局部最优时,侦察蜂采用大步长的搜索方式,搜索最优解。

2 IABC算法

ABC算法在求解未知三维环境路径规划问题时,优化效果较好,但蜜源位置初始化策略及迭代过程中蜜源位置更新方式的简单随机性,影响了初始解的大小和整个算法的收敛速度,即程序完整的运行时间,以及最终解的精度,因此,本文对ABC算法做了如下改进。

2.1 优化蜜源位置初始化分布

在ABC算法中,蜜源位置初始化,按式(1)随机产生N=1/2NP个蜜源,其中NP为总人工蜜蜂数。该初始化分布策略简单随机,在程序实现方面具有很大优势,但随机产生的蜜源之间没有关联性,且蜜源位置的分布没有目的性,这对后续的搜索产生了影响

(1)

(2)

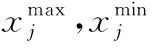
针对以上不足,本文对蜜源位置初始化,采用均值μ=0,方差σ2=1的正态分布方式。如式(2)所示,采用|nodij|代替简单随机数rand,将产生的随机数集中在[0,1]之间,对于正态分布产生不在[0,1]范围的数,用随机数rand代替,使产生靠近0的概率高于接近1的概率,即将蜜源集中分布在Xij位置附近,但又不局限于Xij。这种改变增强初始化的目的性,充分利用先验知识进行高效寻优,为后续搜索提供精度保证。

2.2 优化蜜源位置更新方式

通过对ABC算法的研究发现:ABC算法每轮迭代过程中,新蜜源的产生是在上一轮蜜源附近随机产生,虽然在程序实现方面简单便利,但影响整个程序收敛速度及最终求解精度。因此,本文基于ABC算法建立蜜源位置更新优化数学模型,具体如下:

ABC算法在进行完每轮迭代后,得到当前N个蜜源X1,X2,…,XN,它们的中心蜜源X0比这N个蜜源X1,X2,…,XN中任何一个蜜源含有更多的有效信息,因此,本文将在中心蜜源X0与当前的每个蜜源Xi所围成的领域范围内进行一次搜索,得到新的蜜源Yi。其中

Xi=(xi1,xi2,…,xin),X0=(x01,x02,…,x0n),

Yi=(yi1,yi2,…,yin)

建立中心蜜源数学模型为

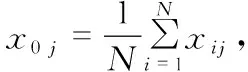
(3)

根据式(3)求得蜜源Xi(1≤i≤N)所对应的新蜜源Yi为

yij=xoj+rand(0,1)(xij-x0 j),j∈{1,2,…,n}

(4)

最后为进一步增强IABC算法的寻优能力,将先前蜜源Xi的适应度值与所求出新蜜源Yi的适应度值做比较,从中选取较优蜜源,提高算法整体收敛速度[13]。

2.3 算法流程

IABC算法流程具体如下:1)进行蜜源初始化,根据式(2),生成N个蜜源,并计算其适应度函数值。2)采蜜蜂根据式(4)在蜜源位置附近寻找新的蜜源。3)若某处的蜜源经历了LimitNum次后仍未找到邻近更优的蜜源,则侦察蜂采用较大步长随机生成蜜源位置。4)采蜜蜂回到蜂巢与跟随蜂共享蜜源信息,根据蜜源适应度跟随蜂遵循轮盘赌法,以一定的概率选择蜜源。5)转回步骤(2)直到迭代m次后,跳出循环。算法流程如图1所示。

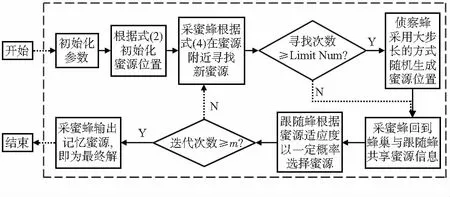
图1 算法流程

3 实验验证与结果分析

3.1 实验环境配置

为验证本文提出方法的可行性,需进行大量仿真实验,为实现算法对比之间的公平性。首先,实验在AMD Ryzen 7,CPU:5800H、512GB内存、3.6GHz主频的计算机上实现,程序采用MATLAB2016a语言实现。使用MATLAB曲面网格划分建立未知三维环境模型,随机在[100×100×100]的区域内构建10个大小不一的山峰,模拟真实环境中的障碍物,设置坐标[1,1,20]处为起始点,图中用正方形标记,坐标[100,100,50]处为目标点,图中用五角星标记。同时采用相同初始化参数:迭代次数m=100，蜜蜂总数Ns=100，采蜜蜂数量/蜜源数量Ne=Ns/2，陷入局部最优判断阈值LimitNum=5。

3.2 算法性能比较

在使用MATLAB软件建立的3组模拟真实环境中,通过采用上述参数设置,分别从路径规划的长度,程序完整运行时间，陷入局部最优的次数,对三种算法的性能进行分析。

实验结果如图2～图4及表1所示,IABC算法与ABC算法规划的路径相比较,IABC算法所规划路径长度相对较短；相较于ABC算法,IABC算法初始最优适应度值大大降低,促使程序完整运行时间相对减少；同时相较于ABC算法,IABC算法陷入局部最优的次数,有了一定的减少,如图2(b)、图4(b)所示,陷入局部最优次数分别从原来的6次降低到2次,原来的8次降到4次。总之,处理机器人在三维未知环境中的路径规划问题,IABC算法比ABC算法更加完善。

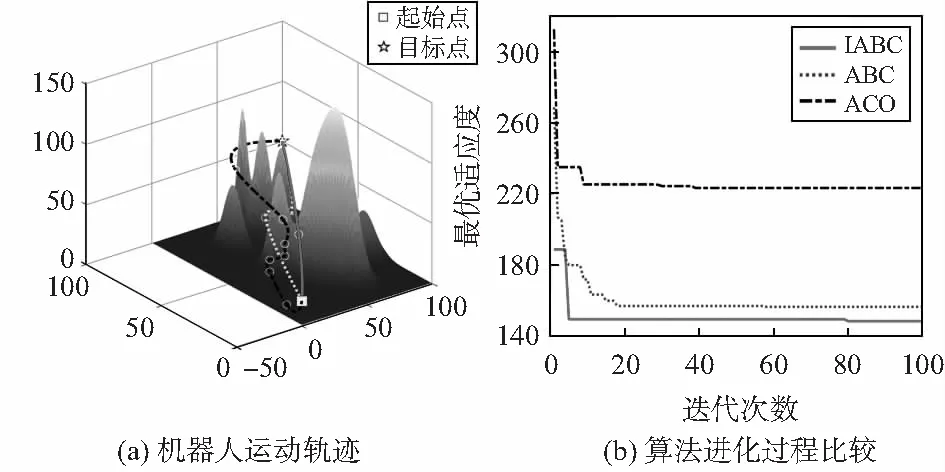
图2 仿真环境一

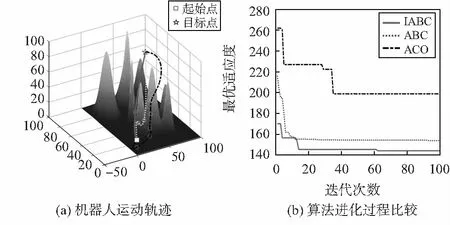
图3 仿真环境二

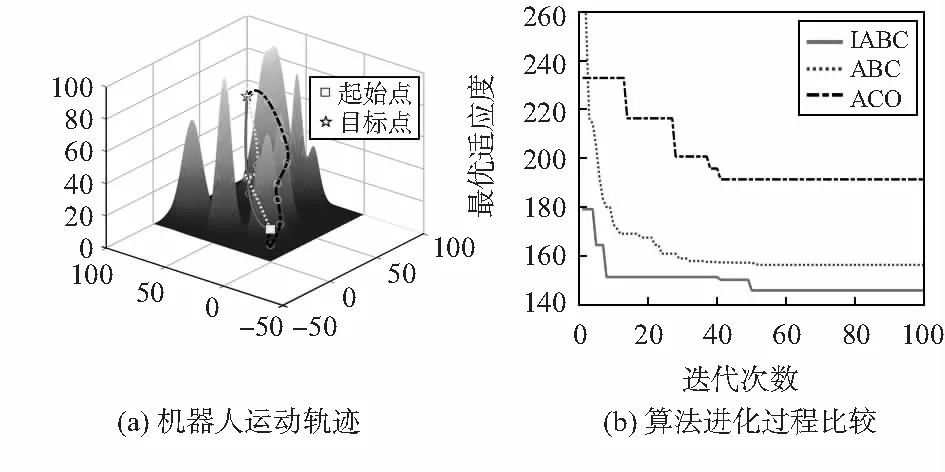
图4 仿真环境三

表1 IABC算法与ABC算法及ACO算法仿真实验结果

同时,为进一步深入验证本文提出方法的可行性,进行了算法横向对比,即IABC算法和ACO算法使用同上述一致的参数设置,解决相同的三维未知环境中的路径规划问题。实验证明:IABC算法相较于ACO算法,虽然陷入局部最优的次数没有明显减少,但所规划的路径距离大大缩短,同时迭代过程中,初始最优适应度值的降低,使得程序收敛速度加快,程序完整运行时间降低。因此,解决该类路径规划问题,IABC算法显然优于ACO算法。其中理论最优路径长度为起始点到目标点的直线距离。

4 结 论

针对三维未知环境中的路径规划问题研究,提出一种基于改进人工蜂群算法的路径规划方法。首先,为提高传统ABC算法中初始化的目的性,并为后续搜索提供精度保证,引入正态分布思想,优化蜜源初始化分布；同时优化迭代过程中蜜源位置的更新方式,构建蜜源中心领域范围内搜索新蜜源的数学模型,由此提出一种改进的人工蜂群算法——IABC算法。其次,使用MATLAB软件曲面网格划分,构建三维未知环境模型。最后,使用MATLAB软件仿真,与传统ABC算法及ACO算法相比,该算法求解精度高、初始最优适应度值明显降低,而且只需要经过较少的几次迭代就可以达到最优适应度值,说明该算法的寻优能力大幅度增强,并且程序完整的运行时间也随着降低。由此可见,本文提出的基于IABC算法的路径规划方法具有可行性。