基于同步整流的反激电源多路闭环控制策略
许 佳,梁亦聪,卢一喆
(西安机电信息技术研究所,陕西 西安 710065)
0 引言
多路输出反激式开关电源由于其体积小、结构简单、成本低,被广泛应用于需多路供电的电子设备中[1]。弹载遥测系统中主要包括FPGA、变频收发器、数据存储器等多种供电电压不同的电子器件,且有小型化、低成本要求[2-3],非常适合使用多路输出反激式开关电源作为其辅助电源系统。
但传统多路输出反激式开关电源仅能闭环控制一路输出的输出电压,其余端口输出电压通过变压器的匝比设定[4],因此,除了闭环输出端口的电压,其他端口输出电压并不准确,尤其是在输入电压小、变压器匝数少的应用场合。此外,多路输出反激式开关电源还存在多路间交叉调节问题,进一步影响了输出电压的精度[4]。这将对遥测系统中数模、模数转换芯片的工作造成影响,从而导致遥测系统测试精度不高。
为解决多路输出反激式开关电源输出电压精度问题已有一些文献作出研究。文献[5]提出了在非闭环输出端口增加Buck变换器以调节输出电压,但这种方式增加了一级变换,成本增加、效率降低。文献[6]提出了一种基于功率分配的控制方式,可以使每路输出均有较高精度,但其需要对每路输出电流采样,增加额外采样电路。文献[7—9]提出了一些改善交叉调整率的方法,例如,优化变压器、加权电压反馈控制等。但这类方法只能将误差分配到各输出端口,以满足各路输出精度需求,不能从根本上消除误差。
本文在反激式开关电源同步整流技术[10-11]的基础上提出一种闭环控制多路输出电压的控制策略,该策略控制同步整流管关断时间,利用同步整流管体二极管导通压降,微调输出电压,达到闭环控制输出电压目的。
1 开关电源的同步整流技术
1.1 同步整流基本原理
开关电源的同步整流技术是将开关电源拓扑中整流或续流二极管替换为MOSFET等全控型器件的技术,旨在利用这些器件的低导通压降,减少电源损耗。在部分拓扑中使用同步整流技术,可以将整体效率提升近10%[12]。本节中以反激式开关电源为例介绍同步整流技术的原理。
图1展示了使用同步整流技术前后的反激式开关电源电路图。同步整流技术中,同步整流器件的开关逻辑为:检测到并联二极管导通后立即导通,检测到自身电流降至0后立即关断。
假设在副边续流时间段内变压器副边有电流is,则不使用同步整流技术的导通压降固定为二极管导通压降,通常在0.7~1.2 V。使用同步整流技术的导通压降为:
Vds=is×Rdson,
(1)
式(1)中,Rdson为功率器件导通电阻,一般MOSFET的导通电阻在毫欧姆级别。使用同步整流技术的导通压降将会大大降低,故其损耗更小。
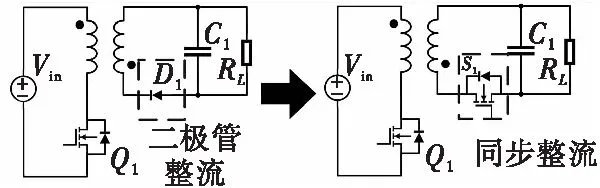
图1 使用同步整流前后的反激式开关电源电路图Fig.1 Diagram of flyback switching power supply using synchronous rectification
1.2 同步整流实现方法
基于变压器次级绕组电压或电流的同步整流驱动方式均存在一些问题[10],而基于检测MOSFET漏源电压的同步整流驱动方式是目前较常用的方式[11,14],图2展示了其实现方式。本文也使用了这种实现方式。
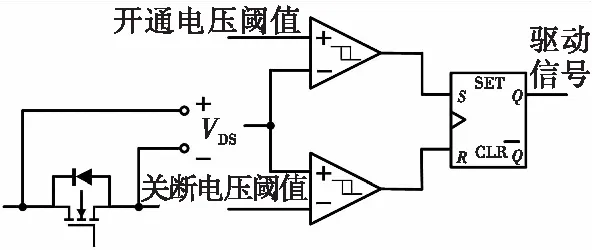
图2 同步整流实现方法示意图Fig.2 Diagram of synchronous rectification implementation method
2 基于同步整流的反激电源多路闭环控制策略
2.1 控制策略原理及分析
第1章关于同步整流技术的介绍中提到,反激式开关电源工作在同步整流状态的副边导通压降远小于二极管整流,而使用同步整流技术的电路可以主动在这两个状态之间切换。本文提出的基于同步整流的反激电源多路闭环控制策略,就是通过闭环控制两种状态的时间,精确控制各路输出电压。
为方便分析,且不失一般性。本节中使用考虑漏感的两路输出反激变换器等效模型,分析变换器在本文提出的控制策略下的工作原理。图3为两路输出反激变换器的等效电路,图中参数均已折算到原边。在该控制策略中,第一路输出功率较大,电压受原边占空比控制,其副边开关管按传统同步整流模式工作;第二路输出功率较小,电压受其同步整流管开通时间控制。
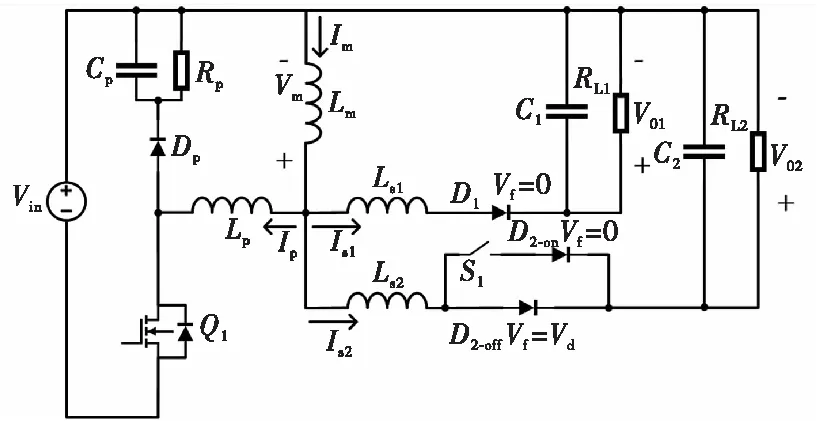
图3 两路输出反激变换器的等效电路Fig.3 Equivalent circuit for two output flyback converters
因为第一路输出按理想的同步整流工作,其副边开关可以认为是一个导通压降为0的理想二极管。而第二路输出在同步整流和二极管整流两个状态切换,在同步整流工作时认为S1闭合,电流从理想二极管D2-on通过;在开关管关闭,认为S1关断,电流流过开关管体二极管D2-off。
2.1.1 电路工作状态分析
使用该策略后,电路工作状态与仅使用二极管整流或完全同步整流的多路反激式开关电源有所区别,为分析输出电压与两种工作模式持续时间的数值关系,需先对电路工作状态进行分析。
由于电流非连续工作模式(DCM)的反激变换器变压器利用率高、体积小[13],下面的分析和设计均按DCM的情况讨论。
首先,对几个关键时间点定义:t0为原边开关管Q1导通时刻,t1为Q1关断时刻,t2为原边漏感电流Ip降至0的时刻,t3为S1关断时刻,t4为第二路漏感电流Is2降至0时刻,t5为第一路漏感电流Is1降至0时刻。图4为整个工作周期关键电路状态波形。
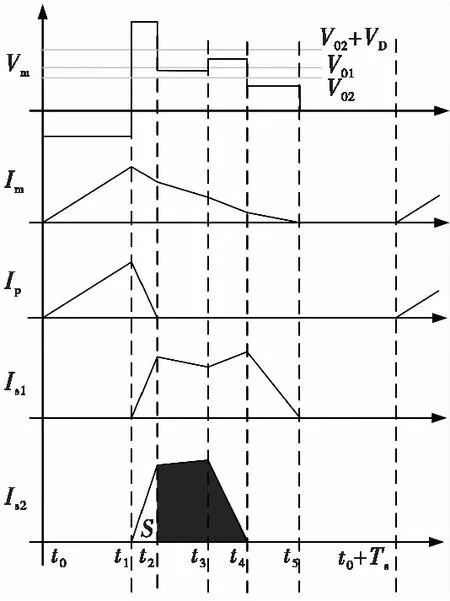
图4 变换器工作状态示意图Fig.4 Schematic diagram of working state of converter
t0~t1时段,电流Im线性上升,副边二极管全部截止Is1与Is2为0,关键状态表达式为:
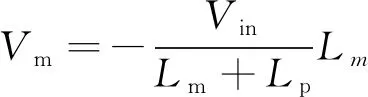
(2)
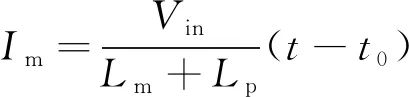
(3)
t1~t2时段,原边电流线性下降,副边电流线性上升,由于该阶段参数在输出功率一定的情况下,工况基本相同,这里仅用Is1-t2、Is2-t2和Im-t2表示此阶段结束时两个输出支路电流和励磁电流。
t2~t3时段,此时两个输出支路均为同步整流工况,关键状态表达式为:
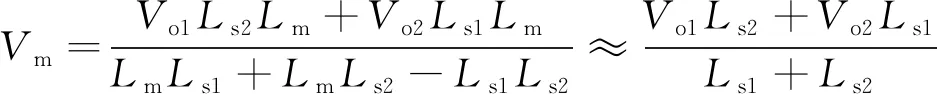
(4)
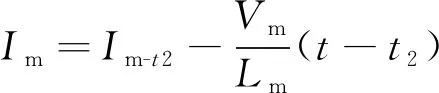
(5)
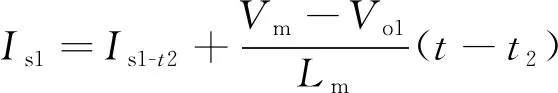
(6)
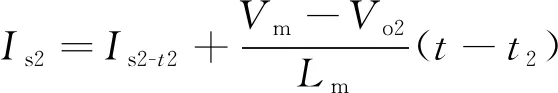
(7)
t3~t4时段,此时第一路为同步整流,第二路为二极管整流,关键状态表达式为:
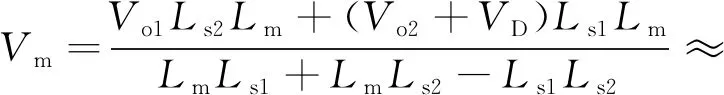
(8)
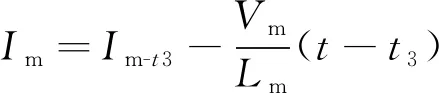
(9)
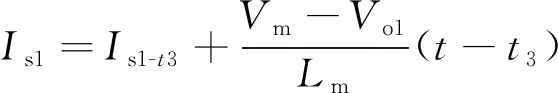
(10)
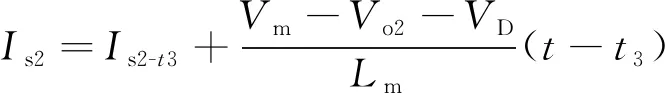
(11)
t4~t5时段,此时第一路为同步整流,第二路电感电流已降为0,关键状态表达式为:
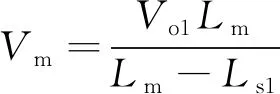
(12)
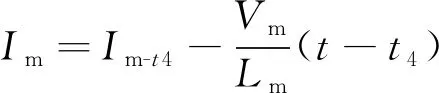
(13)
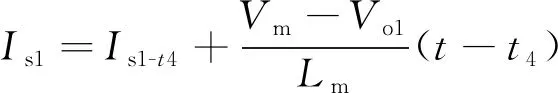
(14)
2.1.2 控制量与被控量关系分析
假设第一路输出电压已经通过控制原边占空比D1稳定在Vo1,第二路输出平均电流为其电流波形面积除以开关周期。在图4中,其电流波形由两部分组成:一部分与原边占空比D1相关,在输出功率一定时其面积固定为S;另一部分则与第二路输出同步管关断时间相关,为图中的阴影部分,这里的关断时间即是所提出的控制策略的控制量。
对第二路输出平均电流进行分析,其平均电流为:
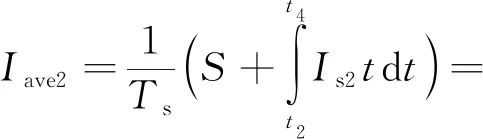
(15)
式(15)中,D2为第二路同步整流占空比,Ks2-23和Ks2-34分别为t2~t3、t3~t4时段内第二路电流斜率,使用式(4)、式(7)、式(8)、式(11)可以得到Ks2-23和Ks2-34。在阻性负载下,存在以下关系:
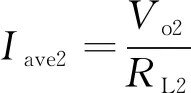
(16)
将Ks2-23和Ks2-34及式(16)带入式(15),可以得到以下方程:
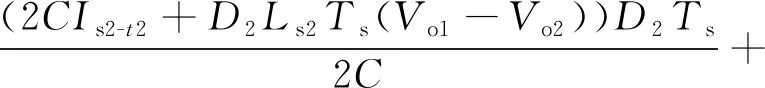
(17)
观察以上方程,其中变量为Vo2和D2,若有Vo1>Vo2,则在D2增大时,Vo2应增大。证明过程:假设D2增大时Vo2减小,则等式左侧前两项增大,第三项为常数,故等式左侧增大,等式右侧减小,等式不成立。因此假设不成立,Vo2是关于D2的单调增函数,可以通过调整D2控制第二路输出电压Vo2。
2.2 系统架构及其实现方法
2.2.1 系统架构
基于前文分析,本文提出了如图5所示的多路闭环控制架构。其中同步整流控制的实现方法在第1.2节中已经介绍。
2.2.2 锯齿波调制及驱动信号逻辑实现
本文提出的多路闭环控制策略可以通过PI控制和锯齿波调制实现。图6中展示了各开关管驱动信号调制和产生过程。
其中,用于控制第一路输出电压的Q1管驱动信号Vg_Q1,由其电压反馈回路中PI调节器输出Vcom1与锯齿载波Vc比较得到。第一路输出的同步整流管S1驱动信号Vg_S1,直接由同步整流电路控制。第二路输出的同步整流管S2驱动信号Vg_S2,由两个信号做“与”逻辑生成。第一个信号为同步整流电路输出的控制信号,用于确定该管开通时刻。第二个信号为控制第二路输出电压反馈回路中PI调节器输出Vcom2与锯齿载波Vc比较得到,用于控制该管关断时刻。
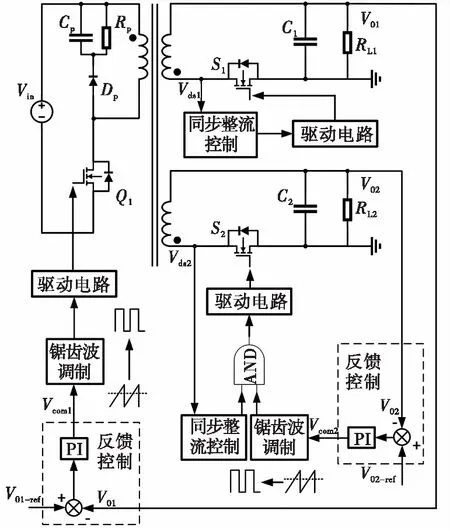
图5 多路闭环控制架构示意图Fig.5 Schematic of multiple closed-loop control architecture
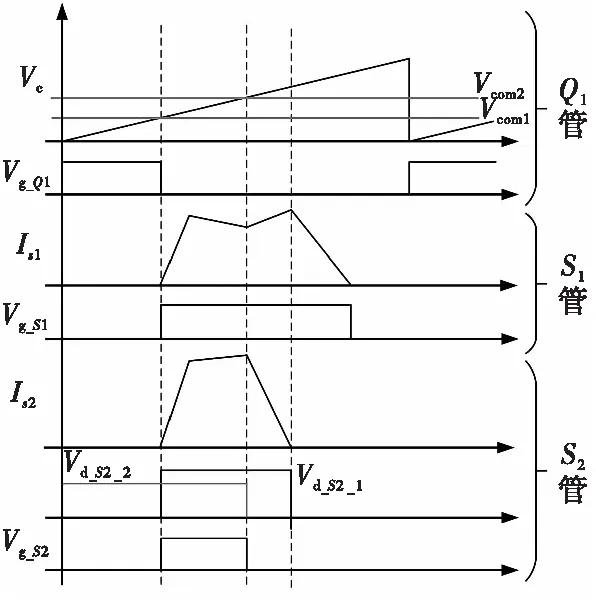
图6 开关管驱动信号调制过程Fig.6 Modulation process of driving signal
2.3 参数设计方法
使用上述控制架构的多路反激电源在硬件参数设计上需满足Vo1>Vo2,即第一路输出在原边的感应电压需要大于第二路输出在原边的感应电压。理由如下,据2.2节的分析,在满足上述条件时,Vo2是关于D2的单调增函数。若不满足上述条件,则公式(17)等号左侧第二项分子括号中的部分可能为负,不能满足Vo2与D2的单调关系。基于上述条件,本节将以设计实例介绍使用本文提出的多路闭环控制策略的多路闭环反激变换器的参数设计方法。
2.3.1 设计指标
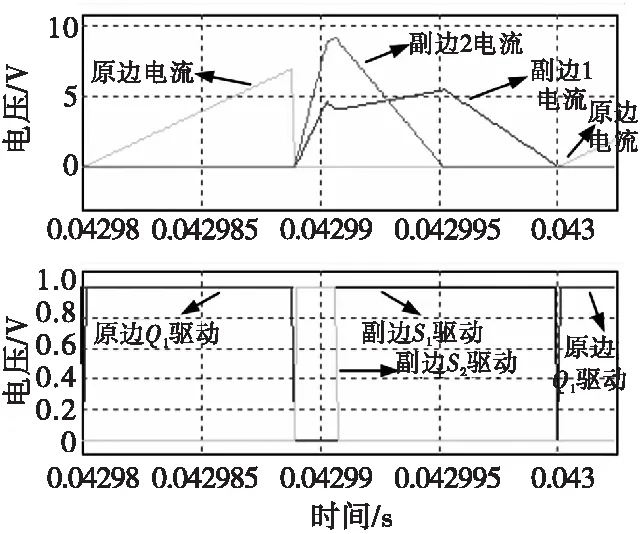
表1中列写了所设计的两路输出反激电源的部分设计指标。
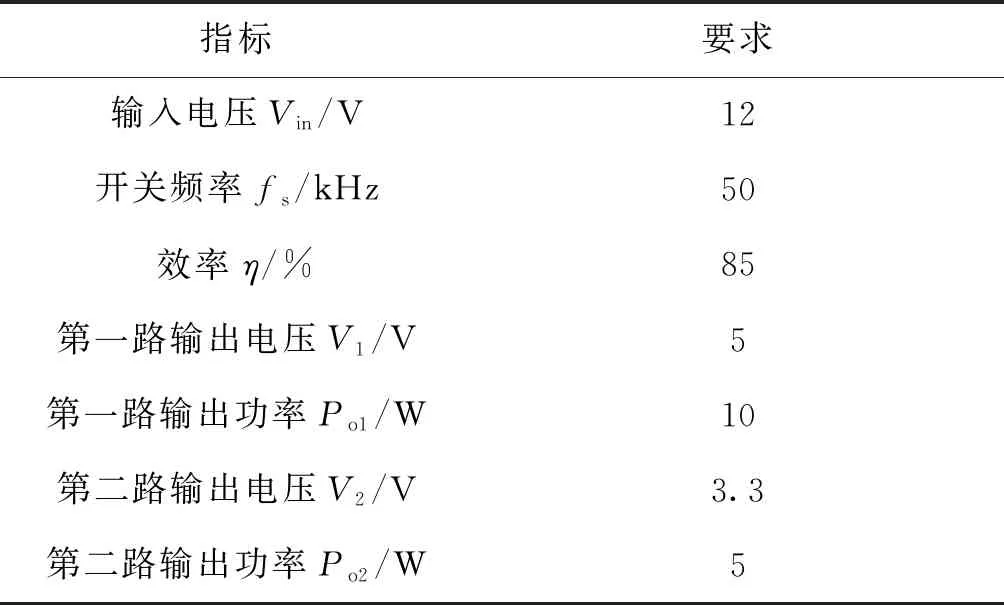
表1 部分设计指标Tab.1 Partial design metrics
2.3.2 电路参数设计
首先确定开关管选型,这里选用德州仪器公司(TI)的CSD17581Q3A,其最大漏源电压30 V,导通电阻3.2 mΩ,反并联二极管压降VSD为0.8 V。按最大漏源电压的70%设计,得到感应电压
VOR=0.7Vds-m-Vin=21-12=9 V,
(18)
之后,计算输入电流平均值
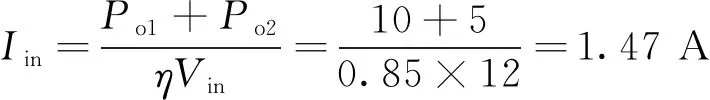
(19)
计算最大占空比
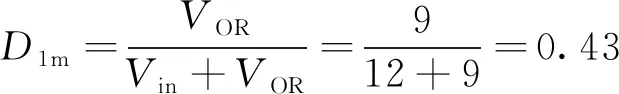
(20)
按临界导通模式(CRM)计算峰值电流
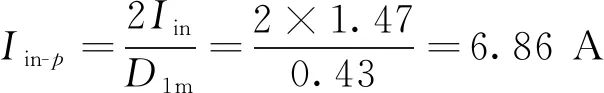
(21)
下面进行变压器设计,首先,计算变压器原边励磁电感
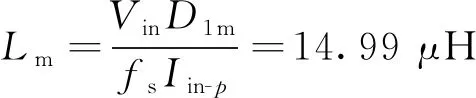
(22)
按文献[15]中的方法估算磁芯大小,最大磁密Bm按0.3 T估算,选择EE19规格的磁芯作为变压器磁芯,其有效截面积Ae为22.3 mm2。
计算原边匝数
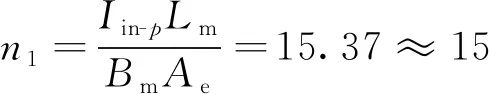
(23)
在设计两个副边绕组匝数时,第一副边匝数向下取整,第二副边匝数向上取整,以保证满足条件Vo1>Vo2,
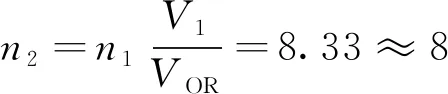
(24)
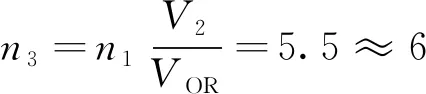
(25)
最后,估算S2在完全同步整流和完全二极管整流时的第二路输出电压,以验算第二路输出电压是否可以达到指标值,
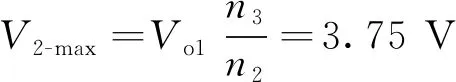
(26)
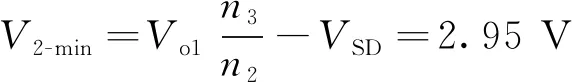
(27)
以上结果满足V2-min 对于指标为表1中参数的两路反激电源,按上述控制策略和参数设计的结果进行仿真,仿真中主要电路参数列在表2中。 按表中电路参数仿真,图7展示了两路输出的稳态输出电压波形。图8展示了变压器3个绕组的电流波形和3个MOSFET的驱动波形。 表2 仿真中主要电路参数Tab.2 Main circuit parameters in simulation 对仿真得到的电压波形进行平均值计算,得到第一路输出电压均值为5.02 V,第二路输出电压为3.29 V。两路输出电压误差均在0.5%以内。驱动信号与变压器电流波形与在第二章中的分析结果一致。 图7 稳态输出电压仿真结果Fig.7 Steady-state output voltage simulation results 图8 变压器电流和驱动信号仿真结果Fig.8 Simulation results of transformer current and driving signals 使用同样的电路参数(针对是否使用同步整流,变压器匝数有微调),用不同控制策略与本文中提出的控制策略进行仿真对比,结果如表3所示。 表3 不同控制策略对比Tab.3 Comparison of different control strategies 本文提出的多路闭环控制策略的效率仅较效率最高的加权电压反馈(同步整流)低约3%。但输出电压精度大幅提升。 本文提出一种基于同步整流的反激变换器多路闭环控制策略。该策略控制同步整流管关断时间,实现了多路输出电压闭环控制。通过变换器等效电路模型的分析和推导,证明了该策略的理论可行性,并给出该策略的控制架构、实现方法和参数设计方法,同时对5 V/12 W,3.3 V/5 W两路输出反激电源进行了参数设计。仿真结果表明,该策略可以实现反激变换器两路输出电压误差均在0.5%以内,额定工况效率超过80%。仿真得到的电路工作波形与本文理论分析一致,证明了该策略理论的正确性、实现方法和参数设计的可行性。 使用该控制策略的多路反激变换器,相比其他控制策略在弹载遥测系统中具有如下优势:多路输出电压精度高,为模数、数模转换芯片提供高精度的供电;使用同步整流技术提高电源效率,可以延长使用电池供电的弹载遥测系统工作时间。故该控制策略在弹载遥测系统等需要高精度、高效率的电子系统中有较好的应用前景。3 仿真结果
3.1 控制策略仿真
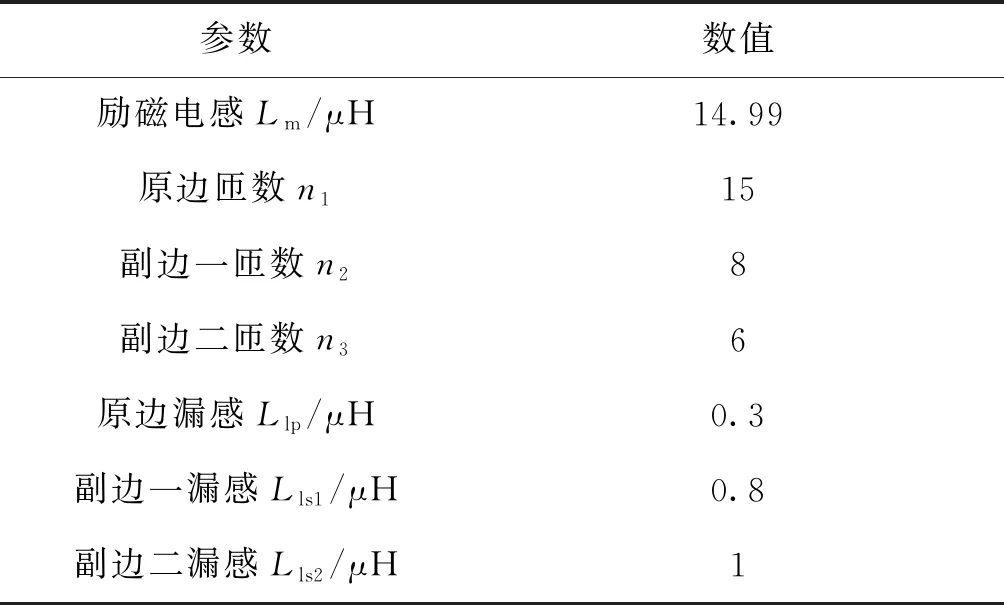
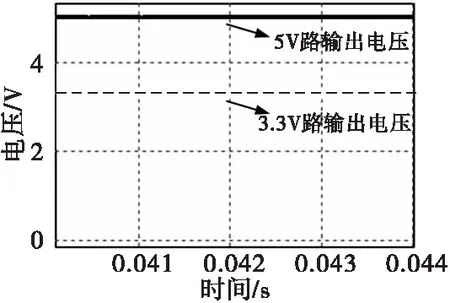
3.2 与其他策略对比
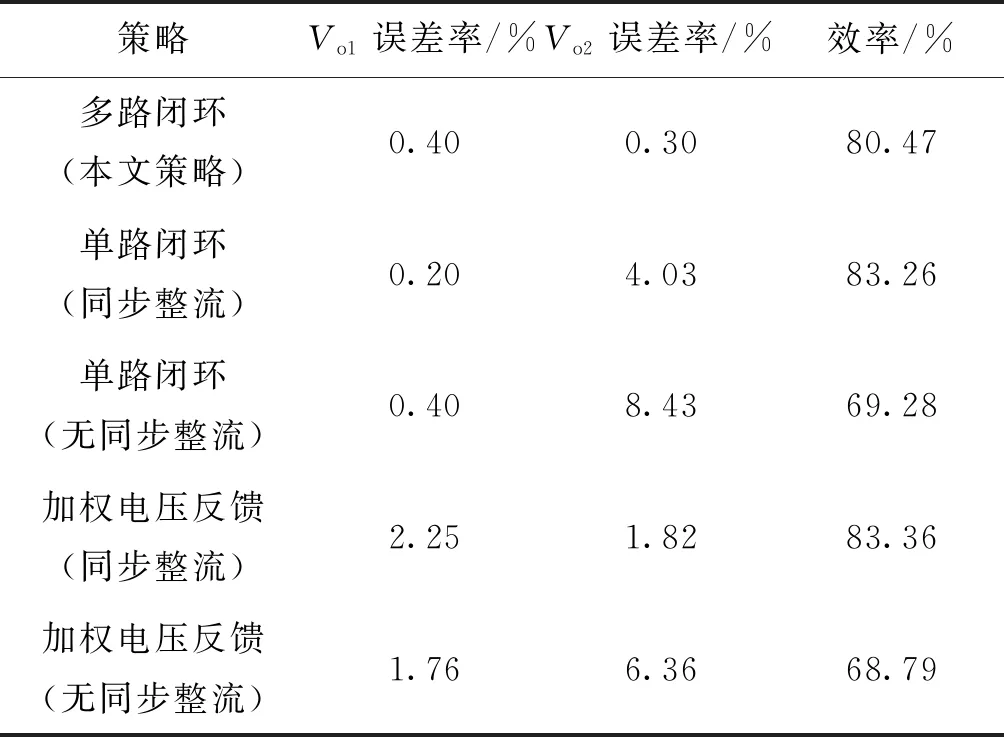
4 结论

