一种舰船轴频电场信号源强度计算方法
李国栋,姜润翔,孙兆龙,刘 琪
(海军工程大学电气工程学院,湖北 武汉 430033)
0 引言
舰船轴频电场因其频率低、传播距离远,线谱特征明显,可被用于水下远距离探测的被动信号源[1-5]。一方面为了能够对己方舰船的轴频电场信号的量级及特性进行评估,另一方面为了有效评价轴频电场抑制装置的有效性[6-7],均需对轴频电场的源强度进行反演计算。
在远场(1.0倍船长)附近,轴频电场可近似视为沿舰船纵向分布的水平时谐电偶极子产生的电场,文献[8—10]利用水平时谐电偶极子对轴频电场信号进行了建模计算。实际上,等效电偶极矩还存在横向、垂直方向的分量,其强度通常明显小于水平方向的等效电偶极矩,但其在近场附近仍然可以产生较大量值的信号,因此,在仅利用沿舰船纵向方向的水平时谐电偶极子对轴频电场建模时,存在近场误差较大的问题。文献[11]提出基于包络信号的建模和源强度计算方法,虽然解决了近场建模的难题,但忽略了轴频电场信号重要的频率特征信息。
由于电场的趋肤效应,舰船轴频电场不同谐波信号在传播相同的距离时,能量衰减比例不同。实际电场探测中,舰船轴频电场在不同的距离会具有不同的频谱,将轴频电场反演源强度分配在各个谐波分量上,可以获得舰船轴频电场在全空间的频谱特性,进而明确舰船电场探测的有效距离和轴频电场信号识别的主要特征。
为了提取轴频电场信号的频率特性,将不同谐波分量分离开,进一步提高探测精度,更清晰地分辨不同船舶的电场信号差异,本文提出一种新的轴频电场源强度计算方法。
1 轴频电场信号
1.1 产生机理
在电化学腐蚀和防腐过程中,无论是腐蚀电流还是保护电流,都将从阳极(船壳、辅助阳极或牺牲阳极)通过海水流向阴极(螺旋桨),再经过尾轴、轴承、联轴器、齿轮等接地结构返回到船壳形成回路[12]。螺旋桨转动时,外部海水扰动引起的船体及螺旋桨与海水的接触电阻变化,内部回路轴地等效电阻Rb的变化均将引起海水中的电流波动,从而在海水中产生以螺旋桨转动频率为基频的轴频电场信号,其中Rb的变化是产生轴频电场的主要因素。
1.2 基本特性
轴地等效电阻Rb的幅值、变化规律与轴的载荷、偏心度、碳刷弹簧的弹性等因素密切相关,一艘中型舰船同种转速条件下的轴地等效电阻Rb如图1所示,其中Rb由轴地电压值除以轴电流(非接触电流传感器测量结果)得到。由图1可发现,轴地电阻的波动值具有明显的随机性,且左轴与右轴的差异较大。
轴地电阻的波动具有随机性,必将导致水下轴频电场信号强度的随机性,因此,在对轴频电场信号建模时,一种合适的方法是对某一时间段内轴频电场信号的包络进行建模,以得到轴频电场信号最大的幅值。需要说明的是,轴地电阻的波动值虽然是随机的,若不同谐波信号的相位值相对稳定,结合幅度变化特征,则有望通过振幅和相位实现对轴频电场信号的建模计算。
轴电流是描述轴频电场的重要特征(实测轴电流与轴频电场的归一化频谱如图2所示),因此本文重点对典型舰船的轴电流特性进行分析。一艘中型舰船航速为9.5 kn时对应的轴电流如图3所示,采用滑动窗(10 s)计算轴电流信号的频谱,连续20 s不同谐波信号的相位时间历程曲线如图4所示。
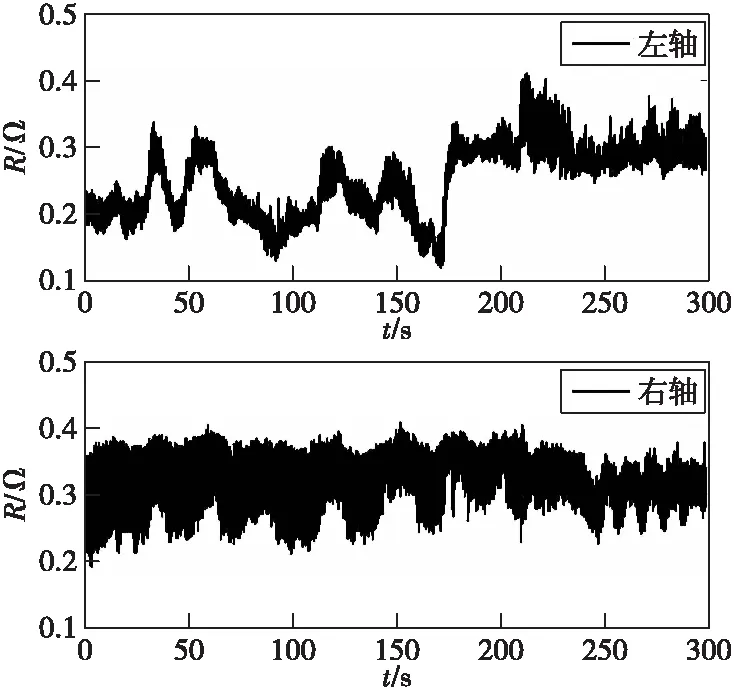
图1 一艘舰船的轴地电阻信号Fig.1 The resistance between shaft and ground
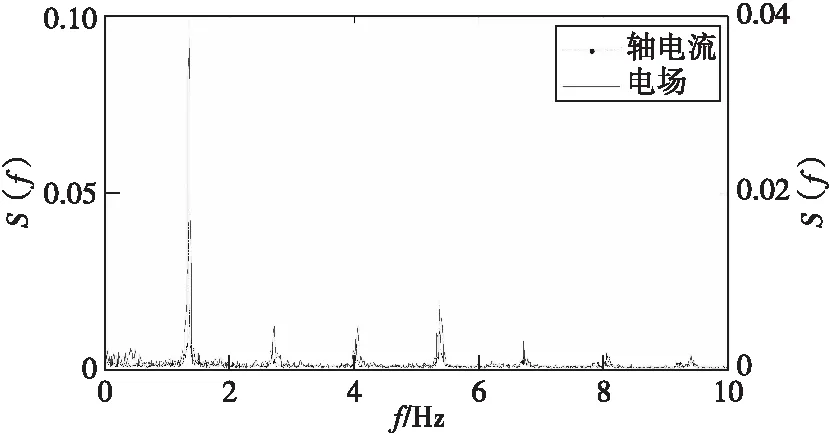
图2 实测轴电流与轴频电场的归一化频谱Fig.2 The normalized spectrum of shaft-rate electric field and shaft current
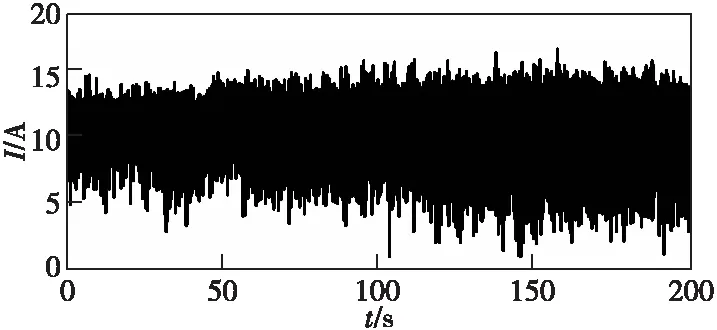
图3 一艘中型舰船航速为9.5 kn时对应的轴电流Fig.3 The shaft current at 9.5 kn speed
由图4可发现,谐波信号的相位值在-180°~180°范围内周期性的变化,且随着谐波信号频率的升高相位周期逐渐减小;对比图3和图4可发现,虽然在20 s时间内,电流信号的强度发生了改变,但其相位值相对稳定不变,这是由轴转动时轴承、联轴器、齿轮等对轴地电阻影响的同步性缘故引起的。
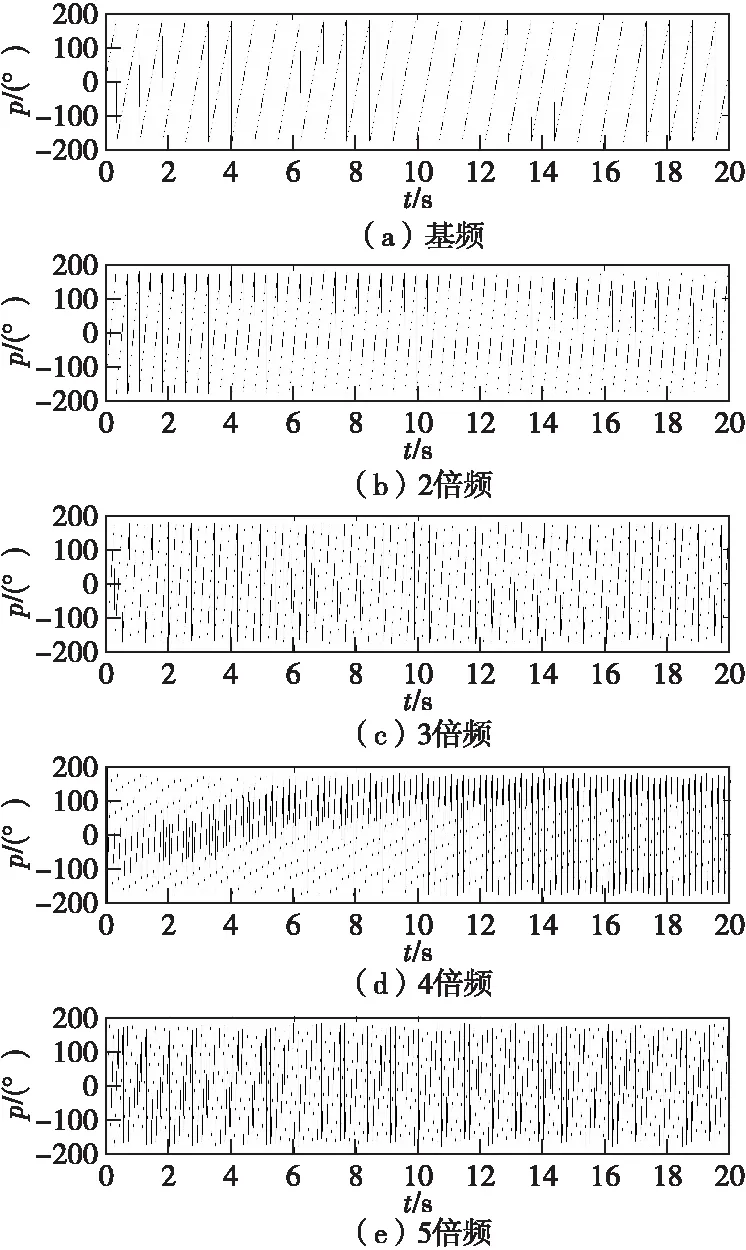
图4 不同谐波信号的相位时间历程曲线Fig.4 The phase-time curves of different harmonic signals
2 轴频电场源强度反演算法
由第1章分析可知,轴频电场的特性与轴电流的特性具有较好的一致性,且轴电流的相位特征具有周期性和稳定性。因此若能根据测量得到的轴频电场计算出不同谐波信号对应源强度的幅度和相角,便可实现对轴频电场信号进行准确建模。一种可行的方法是采用包络信号反演出合成信号的源强度,并根据水下电场谐波信号的分布特征反推出各个谐波对应的源强度。
2.1 基本原理
若将船体表面S分为n个小面源Si,i=1,2,…,n,每个小面源在t时刻对应的等效电荷为Qi(t),则任意一点在t时刻对应的水下电位值
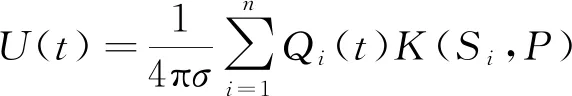
(1)
式(1)中,σ为海水电导率,K(Si,P)为等效点电荷的坐标(xi,yi,zi)到场点P(x,y,z)处的距离函数。在近场范围内,点电荷在空气-海水-海床三层均匀介质条件下有
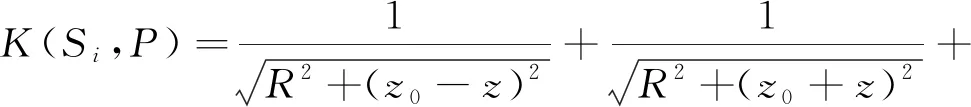
(2)
式(2)中,H为海水深度,R2=(x-xi)2+(y-yi)2,k=(σ-σ1)/(σ+σ1)为海底反射系数,σ1为海床电导率,m为反射层数,实际计算中其上限值可取10~20[13]。
由式(1)、式(2)可知,对于固定场点,其水下电场信号的变化取决于Qi(t),将Qi(t)展开为傅里叶级数的形式,有
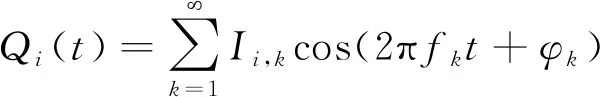
(3)
式(3)中,Ii,k、fk、φk分别为第k个傅里叶级数对应的幅度、频率和相位。
将式(3)代入式(1),有
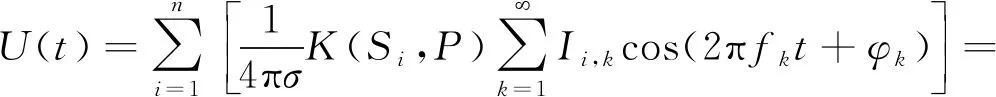
(4)
由式(4)可发现,U(t)与Qi(t)的傅里叶展开式具有一一对应的关系,即U(t)与Qi(t)不同谐波信号对应的幅度关系满足相似性,U(t)与Qi(t)不同谐波信号对应频率、相位具有一致性。在近场(测量水深通常为数十米左右)测量范围内,海水低通滤波器的作用将导致电场信号与点电荷信号的幅度与相位有所偏差,但是由于轴频电场信号的频率通常集中在0.5~30 Hz范围内,在4 S/m的海水中,30 Hz信号对应的波长约为273.8 m,远大于近场的测量距离,因此近场范围内,海水引起的轴频电场相位变化可忽略不计,即可认为电荷强度的幅度、相位与水下电场的幅度、相位具有相似性。
文献[11]和文献[14]提出的基于轴频电场包络信号的反演算法,较好地解决了近场源强度计算的问题。考虑到包络信号反演得到的是舰船通过时间周期内时船体表面等效电荷的最大幅度值|Qi|,并根据水下电场与电荷的对应关系,有
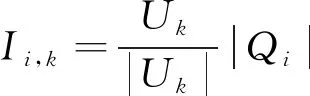
(5)
式(15)中,|Uk|为水下电场对应的最大振幅值。进而得到轴频电场不同谐波信号的源强度为:
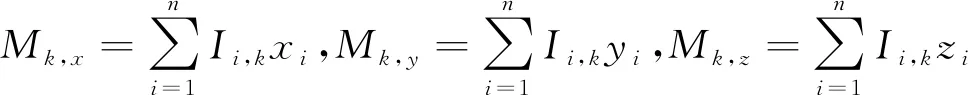
(6)
2.2 线谱提取方法
由2.1节分析可知,对轴频电场不同谐波信号源强度反演的关键是准确提取线谱信号,为此,需要注意以下两点:1) 为了减少运算量,结合轴频电场信号的特征,可计算三分之一倍频程谱;2) 可采用平滑滤波的方法提取线谱信号[15]。
提取线谱信号的具体原理:由于在短时间内,0.5~30 Hz频段范围内的海洋环境背景噪声近似服从正态分布[16],因此不同频带环境噪声的幅度谱也近似服从正态分布,而当舰船轴频电场信号线谱信号出现时,将引起分布特征出现异常。具体计算步骤为:
1) 对时间窗t0内采集得到的轴频电场信号U(t)进行FFT计算,得到U(t)的频谱UFFT,去除UFFT中的直流分量,得到
UFFT=[U0,U1,…,UN],
(7)
式(7)中,N为频点数。
2) 对UFFT进行能量归一化,得到
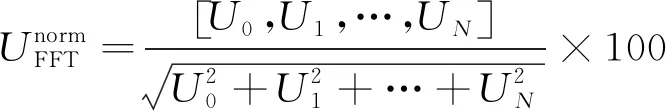
(8)
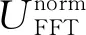
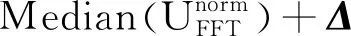
(9)
式(9)中,Median(·)为中值滤波运算符,中值滤波器的长度L通常取3、5、7…,Δ=[Δ0,Δ1,…,ΔN]为固定门限向量,该值可通过仿真计算相同时间内的高斯噪声得到。
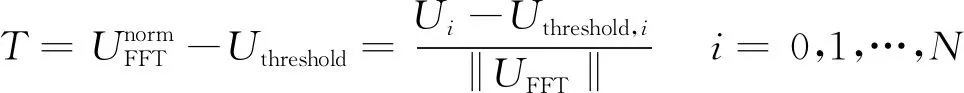
(10)
式(10)中,T=[T0,T1,…,TN]。若Ti≥0,则判断为线谱信号,否则为噪声信号。
2.3 源强度计算基本步骤
在2.1节、2.2节的基础上,确定轴频电场源强度的具体反演步骤如下:
1) 利用轴频电场信号的包络信号反演得到等效电荷强度|Qi|;
2) 计算水下电场信号的傅里叶变换,得到fk、φk、Uk和|Uk|,并按照式(7)—式(10)提取线谱对应的相位值、幅度值;
3) 根据式(5)、式(6)计算得到主要线谱信号对应的等效电流Ik,等效源强度Mk,x、Mk,y、Mk,z。
3 缩比模型试验验证
缩比模型法[17-19]已成为舰船外加电流阴极保护系统设计、腐蚀相关电场特性分布、涂层破损和流速对腐蚀及防腐的影响等研究领域的标准方法。本文利用1∶50缩比模型船模(如图5所示,模型长度L=2.72 m、船宽B=34 cm、吃水深度T=9 cm,船体材料为涂层钢,螺旋桨为镍铝青铜)试验对所提方法的有效性进行了检验。试验水池为玻璃钢池体,池水为配比3.5%的配置海水,配置后经过一段时间的静置,船模提前放置在池中自然腐蚀极化。试验过程中,分别获得了全船位于局部牺牲阳极防腐、全船牺牲阳极防腐、外加电流阴极保护与局部牺牲阳极联合防腐状态等不同阴极保护状态下的数据。

图5 缩比船模Fig.5 Scaled ship model
值得注意的是,由于模型等比例缩小,受测量电极尺寸的影响,难以准确获知轴频电场的Ex、Ey和Ez分量。因此,试验中选择对轴频电场信号的电位U进行测量,测量Ag/AgCl电极分别置于水深24、34、51 cm三个不同深度,每个深度平面3个Ag/AgCl电极的正横距(指测量电极距离船舶龙骨正下方的横向位置偏移)分别为0、17、34 cm,基准Ag/AgCl电极置于水深1.2 m,基准电极距离测量电极的最小距离为4 m。电机拖动装置控制船模以10.08 cm/s的速度匀速通过测量电极上方时,利用微弱电场测量装置实时记录轴频电场的电位信号,系统带宽为Dc~20 Hz,采样频率f=100 Hz,螺旋桨转动频率为280 r/m左右。
图6为全船采用牺牲阳极(参比电位值为-1 015.3 mV、轴电流平均值为40 mA)进行防腐时水深 24 cm,船模通过时的轴频电场信号及其包络值。其中,轴频电场信号在74.5 s过零点,在74.5 s之前轴频电场信号包络与Hilbert包络重合,在74.5 s之后,两者波形反相。
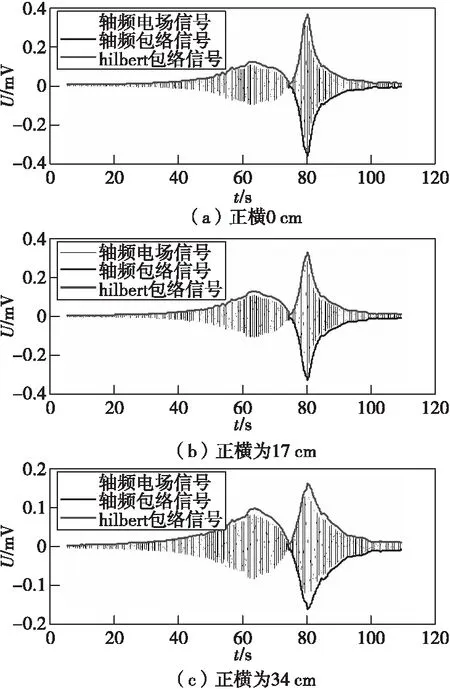
图6 水深24 cm的轴频电场信号及其包络值(牺牲阳极防腐)Fig.6 The shaft-related electric field and its envelope in the depth of 24 cm
根据实测数据与理论计算,舰船电场的等效点电荷应沿中轴线对称分布,反演中将等效点电荷分布在舰船纵向的平行线上是符合实际情况的。利用文献[14]所提的电场点电荷建模方法,在满足对称分布的前提下,为了提高模型换算的精度,所有测量点应保持在K(S,P)泰勒公式展开的收敛半径之外,即需保持最近测量点在其收敛半径之外。在此基础上易知,等效点电荷的最小个数nmin应符合
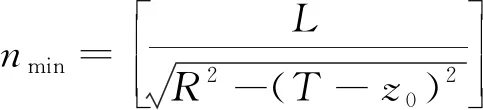
(11)
式(11)中,z0为等效点电荷的垂直坐标值,R为最近测量点到等效点源的距离,nmin应选取大于计算值的最小偶数。本例中选取中轴线点电荷的垂直位置为T,左右舷点电荷的垂直位置为0.5T,计算得nmin为12。
将轴频电场包络的等效36个点电荷分别置于船体中轴线、左舷0.5倍船宽深度、右舷0.5倍船宽深度三条线上,每条线的点电荷数为12个。采用文献[14]所提静电场反演的算法对等效源强度|Qi|进行计算,计算得到的点电荷源强度如图7所示。
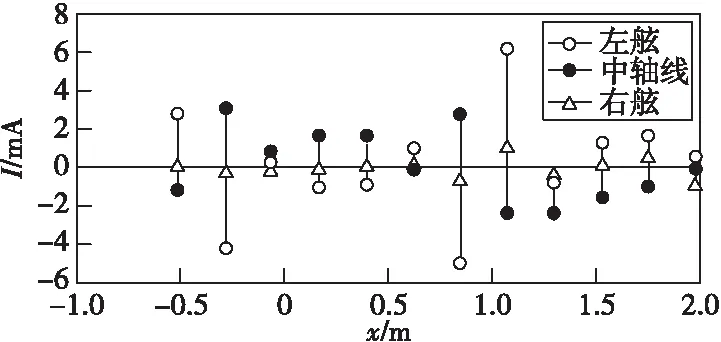
图7 反演计算得到的等效源强度Fig.7 The shaft-related electric field and its envelope in the depth of 24 cm
计算水深为24 cm、正横距为0 cm的水下电场信号三分之一倍频程的对数谱(0 dB对应1 μV),其结果如图8所示。
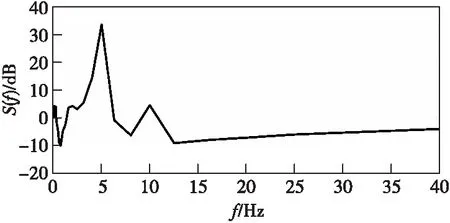
图8 水深为24 cm、正横距为0 cm的水下电场信号的对数谱Fig.8 The logarithmic curve of underwater electric field signal in the depth of 24 cm
仿真计算500组数据长度与轴频电场信号长度一致的高斯噪声信号,取L=3时,统计高斯噪声信号的Uthreshold的方差σ,并按照1倍σ准则设定检测固定门限Δ=[Δ0,Δ1,…,ΔN],有Δk=1.046,k=1,2,…,N。提取的主频分别为5.0 Hz和10.0 Hz(由于采用了三分之一倍频程,与螺旋桨转动基频4.83 Hz有所偏差)。按照式(5)计算得到的频率为5.0 Hz与10.0 Hz的谐波信号的源强度相对于|Qi|的比值分别为1.0、0.035 8,进而按照式(6)计算得到的源强度值如表1所示。
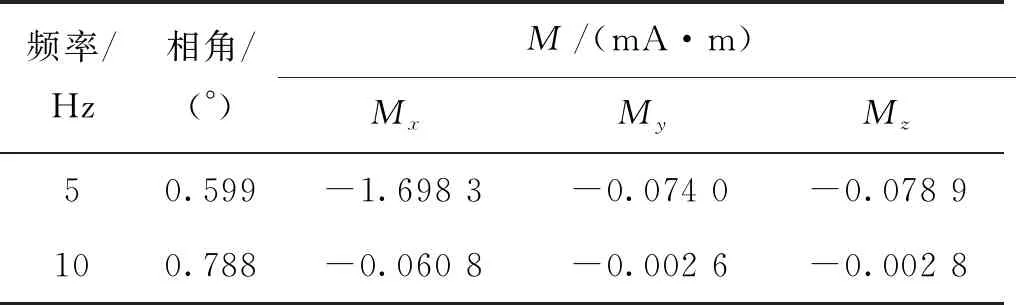
表1 计算得到不同谐波信号的等效源强度Tab.1 The equivalent source strength of different harmonic signals
为了验证反演计算得到的源强度是否正确,将反演计算得到的源强度代入式(4),对正横距为0 cm,深度分别为34 cm和51 cm的轴频电场信号进行反演,其结果分别如图9和图10所示。
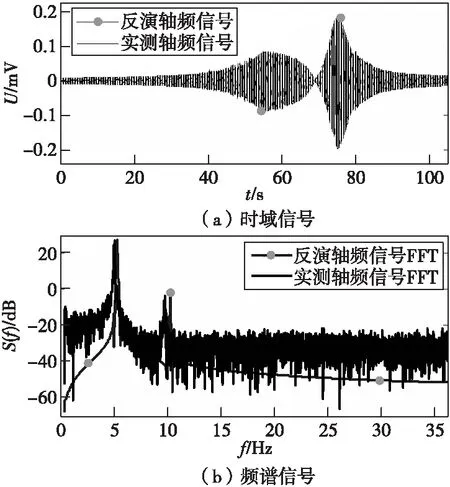
图9 水深34 cm时的轴频电场信号Fig.9 The shaft-related electric field in the depth of 34 cm
由图9和图10可发现,反演得到的轴频电场信号与实测轴频电场信号的时域波形具有良好的一致性,虽然换算出的线谱对应的频率值与真实线谱对应的频率值有所偏差(三分之一倍频程引起的误差),但是其幅度值差别较小,深度分别为34 cm、51 cm时,基频频谱值差分别为0.44 dB和1.85 dB,二倍频频谱值差别分别为2.24 dB和2.55 dB,基频频谱实测峰值分别为28.1 dB和26.4 dB,频谱相对误差分别约为8.0%和9.7%,证明了算法的有效性。
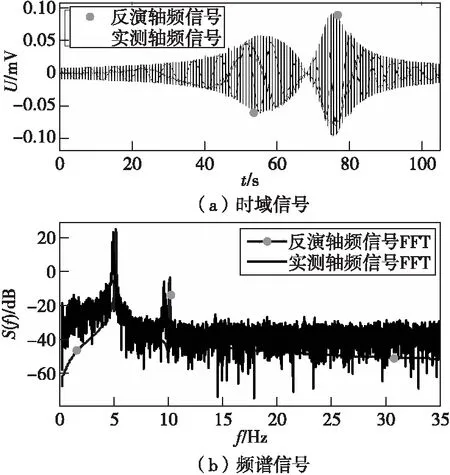
图10 水深51 cm时的轴频电场信号Fig.10 The shaft-related electric field in the depth of 51 cm
为了进一步验证所提方法的有效性,分别利用局部牺牲阳极防腐状态(状态1)和外加电流阴极保护与局部牺牲阳极联合防腐状态(状态2)下的轴频电场数据进行检验,其结果如表2所示。状态1、2时对应的轴电流平均值分别为:28 mA和32.5 mA,反演误差均为正横距为0 cm时的数据结果。由表2可知,所提方法能够有效反演出不同谐波信号的轴频电场源强度,0.7倍船宽深度向1.0倍、1.5倍船宽深度换算时,谐波信号的频谱绝对误差小于3 dB,相对误差小于12%。
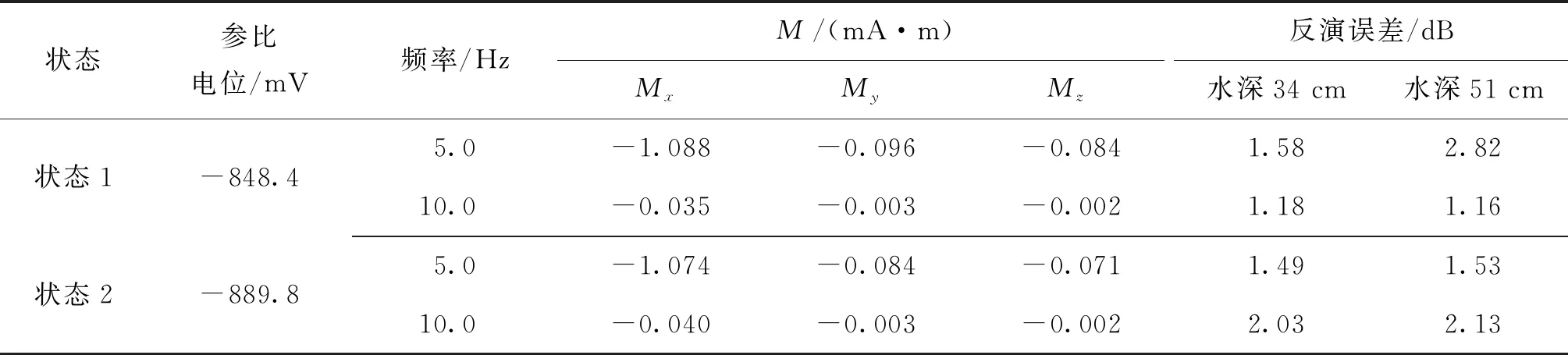
表2 不同船体状态条件下轴频电场信号源强度计算结果Tab.2 The strength calculation results of shaft-frequency electric field signal source under different hull states
需要说明的是,当水下电场信号的信噪比较差时,在计算频谱的过程中,主要线谱的判别误差将导致反演计算出的源强度出现较大的误差值。图11为缩比模型自然腐蚀状态(参比电位为-603.6 mV,轴电流平均值为13 mA)条件下,反演得到的轴频电场信号与实测轴频电场信号频谱图。由图11可发现,在3.15 Hz附近出现了虚假线谱特征,从而导致在5 Hz主频附近出现了近10 dB的误差,频谱相对误差已接近50%。
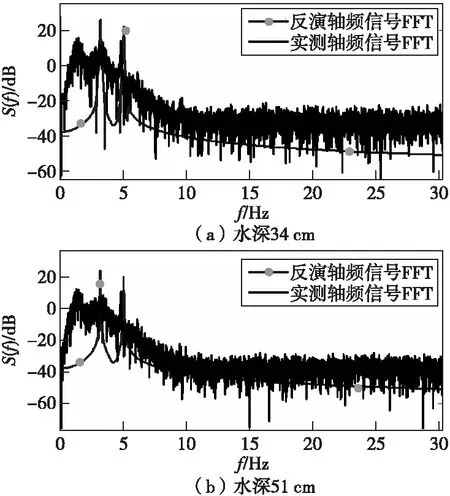
图11 自然腐蚀状态条件下轴频电场信号频谱图Fig.11 The spectrum of shaft-frequency electric field signal under natural corrosion condition
4 结论
为了解决不同谐波频率轴频电场信号等效源强度的求解问题,本文将谐波信号源强度的振幅和相位与水下电场信号对应谐波频率的振幅和相位联系起来,在反演出轴频电场包络信号的等效源强度的基础上,根据水下电场谐波信号的幅值和相位反推出各个谐波对应的源强度。缩比船模试验结果表明,在较好的信噪比条件下,所提方法能够较好地实现对谐波信号源强度的准确计算。下一步研究工作的重点是,利用实船试验进一步验证所提方法的有效性。

