基于雷达数据融合与多模型组合落点坐标预测

田 珂，段鹏伟，常华俊

(中国人民解放军63861部队，吉林 白城 137001)

0 引言

靶场试验中，通常利用连续波雷达测试某型火炮发射弹丸的落点坐标，同时利用初速雷达测试弹丸的炮口初速。但是在试验过程中，有时会出现雷达故障、太阳光线变化导致红外未启、火炮故障导致雷达无法准确测试弹丸信号等突发性故障，这些突发问题都会导致连续波雷达无法准确测试出弹丸的落点坐标。数据缺失成为影响试验任务圆满完成的一大弊端，关系到能否对弹丸和火炮性能进行准确鉴定，所以采用合理的办法预测出未测弹丸的落点坐标就成为一项关键性的任务。目前预测弹丸落点坐标的方法主要有以下几种：文献[1]利用扩展卡尔曼滤波的方法根据修正弹参数预测非修正弹落点，往常需要各打一组修正弹和非修正弹，才能对落点进行比对分析，卡尔曼滤波方法减少了实际射弹量，具有良好的预测精度，但是前提要知道修正点前的实测弹道参数；文献[2]提出了基于摄动原理的分段预测控制法，解决了PP预测法难以快速适应环境与目标的问题，具有较高的预测精度，但是该方法需要提前知道基准弹道和发射初始条件；文献[3]利用弹丸线性理论简化了6自由度方程，推导出了弹丸转向幅值和角度的计算公式，计算结果良好，但条件是不考虑风速和重力的影响；文献[4]提出了通过修正弹丸线性理论进行快速弹道预测的方法，计算精度较高，但是为了保证精度，必须周期性的更新弹道，计算量太大，提升了复杂度。这些方法都或多或少有一定的建模前提，当前提条件无法满足时，建模就遇到了一定难度。由于弹丸的落点坐标包含射程(x)、横偏(z)和高程(y)，均属于一维数据，当已测数据量较少时，可以采用GM(1,1)灰色模型进行预测[5]；但是单一模型的预测精度通常不高，而且落点坐标是随机性非常强的数据，同时还包含一定的线性特征，所以选择把初速雷达的数据和连续波雷达的数据进行融合，建立从初速雷达的径向速度、炮口初速到连续波雷达的落点坐标之间的支持向量回归机、BP神经网络、遗传算法优化LSSVM等非线性映射模型，然后把连续波雷达没有测到而初速雷达测到的弹丸的径向速度、炮口初速代入到建立好的模型中，就可以预测出未测弹丸的落点坐标。该方法的优点是当连续波雷达的数据出现缺失时，可以利用初速雷达的数据预测出连续波雷达的数据，克服连续波雷达数据缺失导致无法建模的瓶颈，有效解决建模条件无法满足时模型无法建立的弊端。最后再把GM(1,1)模型预测值、支持向量回归机预测值、BP神经网络预测值和遗传算法优化LSSVM预测值进行组合，得到多模型组合预测值，组合模型能够克服单一模型预测精度不高的缺陷[6]。

1 单项模型建模原理

1.1 GM(1,1)灰色模型建模原理

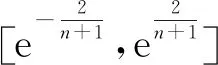
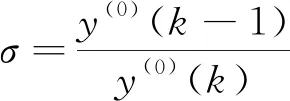
(1)

对数据序列y(0)进行一次累加生成新的数据序列，求解对应的微分方程，再进行一次累减，得到y(0)的预测模型如式(2)所示。常用后验差比值C和小误差概率P检验GM(1,1)模型预测结果的好坏，对应的检验标准如表1所示[9]。

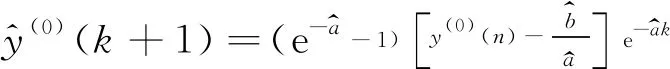
(2)

表1 GM(1,1)预测结果评价表Tab.1 GM (1,1) prediction result evaluation table

1.2 支持向量回归机建模原理

支持向量回归机(SVR)是支持向量机(SVM)在回归领域的应用，针对训练样本D={xi,yi}，找到一个平滑的回归函数模拟其输入输出关系，当有新的输入时，通过该回归函数也能给出相对准确的输出。针对线性问题，设回归函数如式(3)所示[10]：

f(x)=ωx+b。

(3)

要保证回归函数相对平滑，就要求解式(4)的最小值：

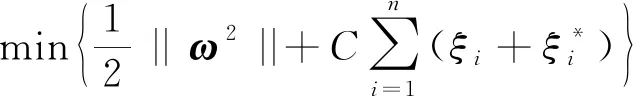
(4)

引入拉格朗日函数，回归函数就转化为式(5)，针对非线性问题，引入核函数k(xi,xj)代替内积函数(xi·x)，回归函数就转化为式(6)所示。

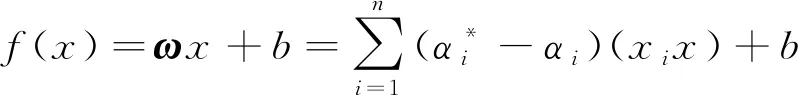
(5)

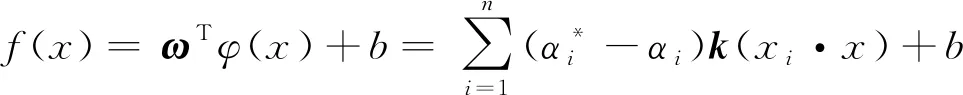
(6)

1.3 BP神经网络建模原理

BP神经网络是常用的人工神经网络模型，是一种多层前馈神经网络，特点是信号前向反馈，误差反向传播。在前向传递中，输入信号从输入层经隐含层处理后，从输出层输出，如果输出层得不到期望的输出，则转入反向传播，同时调整网络链接权值和神经元阈值，使预测输出逼近期望输出[11]。研究表明3层BP神经网络能够用相应的输入向量和输出向量逼近任何有理函数[12]，所以选用3层BP神经网络预测弹丸落点坐标，拓扑图如图1所示。隐含层神经元节点的作用是从样本数据中提取知识，并储存内在的规律，节点数越少，模型获取信息的能力就越差，节点数过多，又会出现过拟合的现象，所以隐含层神经元个数采用式(7)进行确定，q为隐含层节点数，s为输入层节点数，o为输出层节点数，h为1～10的常数[13]。

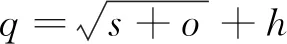
(7)

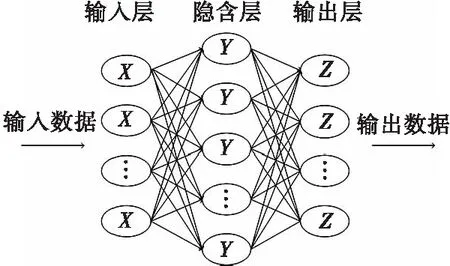
图1 3层BP神经网络拓扑图Fig.1 Topology of three-layer BP neural network

1.4 遗传算法优化LSSVM建模原理

LSSVM是最小二乘支持向量机，是在标准支持向量机的目标函数中增加了误差平方和项[14]，所以最小二乘支持向量机回归函数的优化目标转化为式(8)和式(9)所示，γ为正则化参数，e为误差向量，b为偏置量。

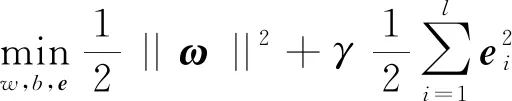
(8)

yi=ωφ(xi)+b+ei。

(9)

针对线性问题和非线性问题，最小二乘支持向量机的回归函数分别与式(3)、式(6)基本一致。LSSVM算法中包含两个敏感参数：核函数参数和正则化参数，通过合理的选择这两个参数可使LSSVM的泛化能力得到提高[15]。为了得到最佳的核函数参数和正则化参数，选择采用遗传算法从众多的参数中搜寻出最优的两个参数。遗传算法是一种通过模拟自然界生物进化过程来搜索最优解的方法，根据确定的适应度函数，采用遗传算子对种群中的个体进行操作，通过在个体间不断交换染色体信息，使种群得以进化，最终使最优的个体得以保留[11]。遗传算法搜寻LSSVM核函数参数和正则化参数的步骤如图2所示。

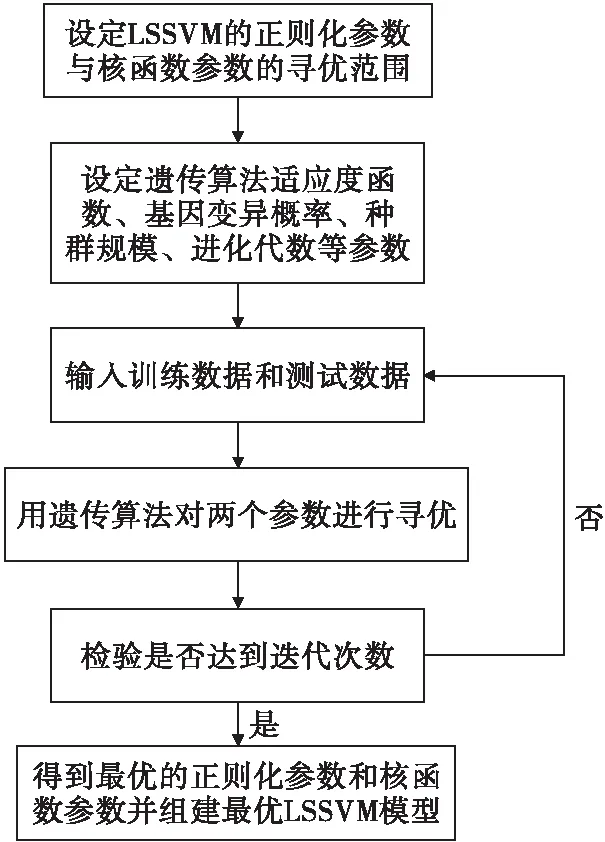
图2 遗传算法搜寻LSSVM最佳参数过程Fig.2 Genetic algorithm searching for the best parameters of LSSVM

2 雷达数据融合与多模型组合的落点坐标预测

2.1 雷达数据融合的原理

由于两台雷达测试的是同一发弹丸，它们测试的径向速度基本是一致的，这是两台雷达内在的关联性，所以选择从初速雷达测试的每发弹丸的径向速度中，把0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5 s的径向速度和测试的弹丸炮口初速作为输入向量，把连续波雷达测试的落点坐标中的射程x、高程y、横偏z分别作为输出向量，建立从输入向量到输出向量的非线性映射模型，即建立了径向速度与射程x、径向速度与高程y、径向速度与横偏z3个神经网络模型，同时利用训练数据训练模型，然后再把连续波雷达没有测到而初速雷达测到的输入向量代入到所建模型中，就可以预测出缺失的弹丸的落点坐标，两台雷达试验现场的布站位置如图3所示。初速雷达测量时间通常设为1 s，计算径向速度的时间间隔设为0.001 s，测试到弹丸信号以后，按照“瀑布图搜索、速度平滑、初速计算”等步骤就可以计算出弹丸的炮口初速，然后在“速度结果”中就可以查看到雷达测试的每个时刻的径向速度了。连续波雷达测试的弹丸落点坐标是根据弹丸的飞行坐标按照雷达自身算法递推出来的，雷达测试飞行坐标的时间间隔也是0.001 s。

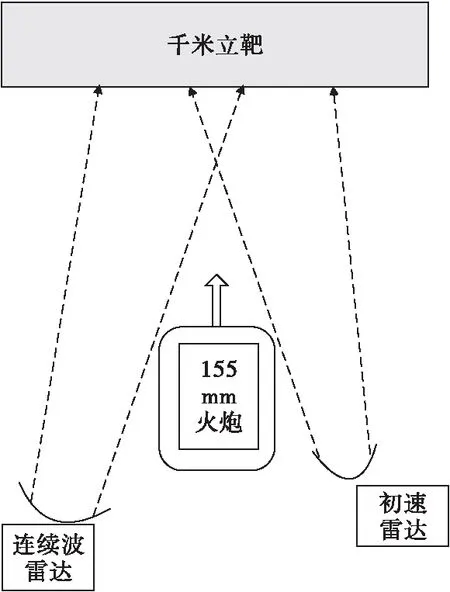
图3 初速雷达和连续波雷达试验现场布站示意图Fig.3 Schematic diagram of initial velocity radar and continuous wave radar test site layout

2.2 多模型组合原理

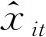
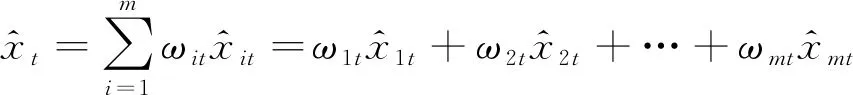
(10)

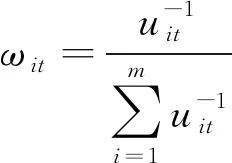
(11)

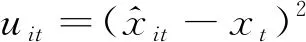
(12)

3 实验验证

实验验证选择RStudio软件环境进行数据分析、统计建模及数据可视化。选取某型155 mm火炮落点坐标实测数据进行验证分析。连续波雷达测试的8发弹丸的落点坐标三维示意图如图4所示，二维示意图分别如图5、图6、图7所示，所有数据及坐标轴刻度都是在原始数据上进行了数量级缩减。

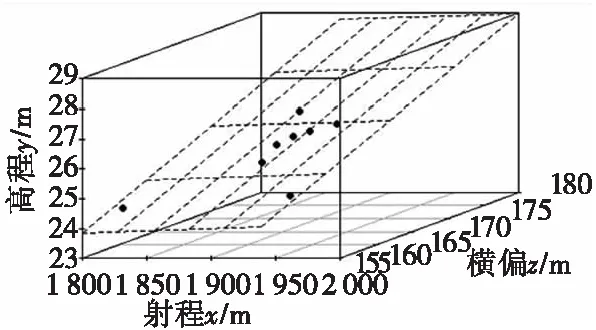
图4 某型155 mm火炮射击弹丸落点坐标实测值三维示意图Fig.4 Three dimensional schematic diagram of measured values of projectile impact point coordinates of a 155 mm gun

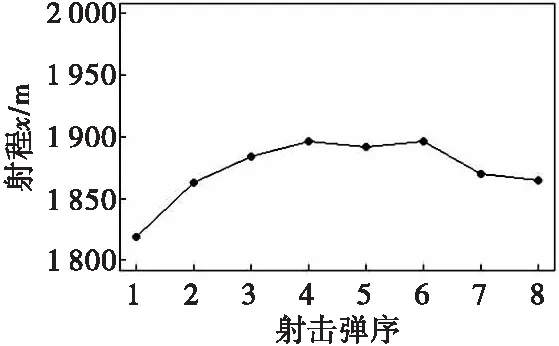
图5 弹丸落点坐标射程x的实测值变化曲线Fig.5 Variation curve of measured value of projectile impact point coordinate range x

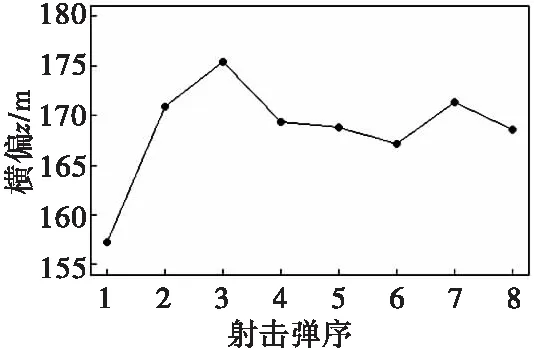
图6 弹丸落点坐标横偏z的实测值变化曲线Fig.6 Variation curve of measured value of transverse deviation z of projectile impact point coordinate

初速雷达从测试的8发弹丸中，每发弹丸选取的9个径向速度变化曲线如图8所示，初速数据变化曲线如图9所示。把初速雷达测试的径向速度和弹丸初速作为自变量，连续波雷达测试的落点坐标作为因变量，检验其相关系数，得知相关系数均不为零，说明自变量与因变量之间存在因果关系，自变量有利于提升预测因变量的准确性，因此，选择建立初速雷达到连续波雷达之间的非线性映射模型是合理的。

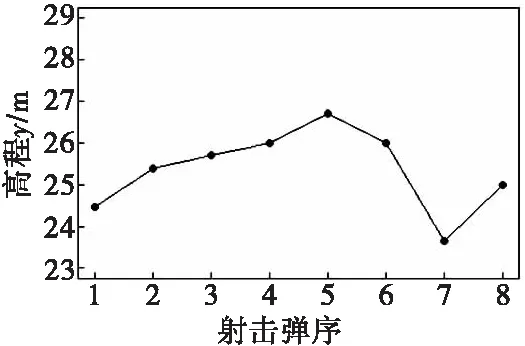
图7 弹丸落点坐标高程y的实测值变化曲线Fig.7 Variation curve of measured value of coordinate elevation y of projectile impact point

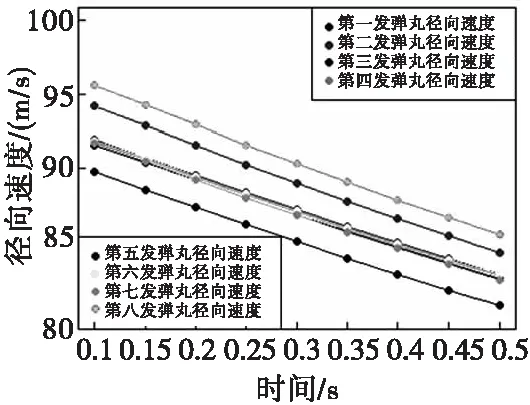
图8 初速雷达测试的8发弹丸的径向速度关系曲线Fig.8 Radial velocity relation curve of 8 projectiles tested by muzzle velocity radar

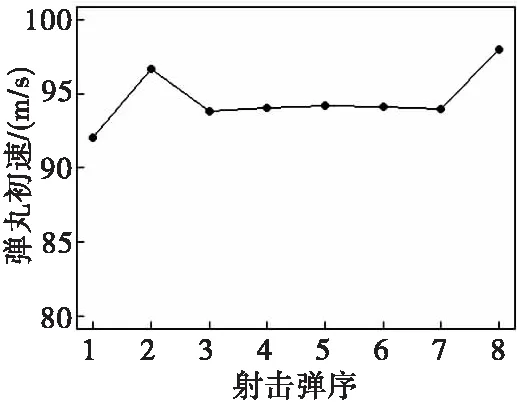
图9 初速雷达测试的8发弹丸的初速数据变化曲线Fig.9 Muzzle velocity data change curve of 8 projectiles tested by muzzle velocity radar

3.1 预测射程x

针对射程x，选择把第1～4发弹丸作为训练数据，第5～8发弹丸作为测试数据。第1～4发弹丸的级比为(0.976 328 5、0.988 696 1、0.993 462 3)，均处于区间(0.670 32、1.491 825)中，符合建立GM(1,1)灰色模型的前提条件，建模预测结果显示后验差比值C=0.041 788 13，小误差概率P=99.893 35%，预测等级为：好；支持向量回归机选择把“radial”作为核函数，其余参数选择系统默认值；BP神经网络根据输入向量个数s=10，输出向量个数o=1，根据式(7)并反复试验后确定隐含层神经元个数q=6，同时将误差精度设为0.01，最大迭代次数设为2 000，最后经过21次迭代算法成功收敛；利用遗传算法进行参数寻优时，选择把径向基核函数作为最小二乘支持向量机的核函数，核函数的参数和正则化参数的寻优范围设置为0～600，种群规模设为400，最大迭代次数设为50，基因突变的概率设为0.01，把第1～4发弹丸中的第1～2发弹丸再作为训练数据，第3～4发弹丸再作为测试数据，并把该测试数据的均方误差作为适应度函数，最后搜寻出的最优参数分别为，核函数参数为7.929 345，正则化参数为264.984 774，把两个参数带入到最小二乘支持向量机中就可以进行预测了；利用四个模型建模预测并根据组合模型建模原理，就可以得到第5～8弹丸射程x的实测值与所有模型预测值如表2中射程x所示，关系曲线如图10所示。

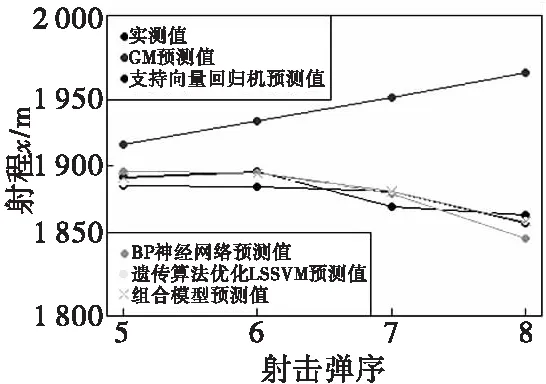
图10 第5～8发弹丸射程x实测值与所有模型预测值关系曲线Fig.10 Relationship curve between the measured range x of the 5th to 8th rounds of projectile and the predicted values of all models

根据表2和图10可以看出，组合模型预测值最接近实测值。经过计算得到，GM(1,1)模型预测值与实测值的平均相对误差为3.22%，支持向量回归机预测值与实测值的平均相对误差为0.458%，BP神经网络预测值与实测值的平均相对误差为0.439%，遗传算法优化LSSVM预测值与实测值的平均相对误差为0.328%，四个模型构成的组合模型预测值与实测值的平均相对误差为0.249%，组合模型预测精度最高。

3.2 预测横偏z

预测横偏z时，选择把第1～4发弹丸作为训练数据，第5～8发弹丸作为测试数据。第1～4发弹丸的级比为(0.920 421 3、0.974 344 4、1.035 419 1)，处于区间(0.670 32、1.491 825)中，符合建立GM(1,1)灰色模型的前提条件，预测结果显示后验差比值C=0.213 459，小误差概率P=98.648 79%，预测等级为：好；支持向量回归机选择把径向基核函数“radial”作为核函数，其余参数选择系统默认值；BP神经网络根据输入输出向量个数结合式(7)选择把隐含层神经元的个数设为6，误差精度设为0.01，最大迭代次数设为2 000，最后经过19次迭代算法成功收敛；遗传算法优化LSSVM把两个参数的寻优范围设为0～600，种群规模设为400，最大迭代次数设为50，基因突变概率设为0.01，最后搜寻出的核函数的参数为2.297 642，正则化参数为547.589 754；最后得到第5～8发弹丸横偏z实测值与所有模型预测值如表2中横偏z所示，关系曲线如图11所示。

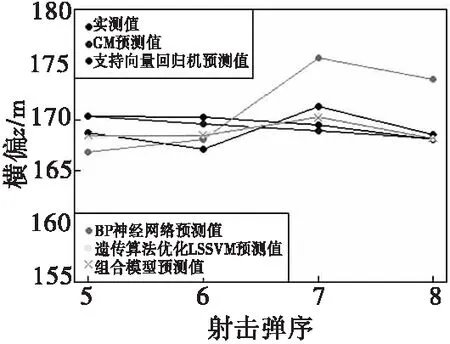
图11 第5～8发弹丸横偏z实测值与所有模型预测值关系曲线Fig.11 Relation curve between measured value of transverse deviation z of the 5th to 8th rounds of projectile and predicted value of all models

根据表2和图11可知，组合模型预测值最接近实测值。经过计算得到，GM(1,1)模型预测值与实测值的平均相对误差为1.02%，支持向量回归机预测值与实测值的平均相对误差为1.05%，BP神经网络预测值与实测值的平均相对误差为1.95%，遗传算法优化LSSVM预测值与实测值的平均相对误差为0.472%，四个模型构成的组合模型预测值与实测值的平均相对误差为0.454%，所以组合模型预测精度最高。

3.3 预测高程y

预测高程y时，选择把第1～4发弹丸作为训练数据，第5～8发弹丸作为测试数据。第1～4发弹丸的级比为(0.962 992 1、0.988 326 8、0.988 461 5)，处于区间(0.670 32、1.491 825)中，符合建立GM(1,1)灰色模型的前提条件，建模结果显示后验差比值C=0.001 127 259，小误差概率P=99.997 36%，预测等级为：好；支持向量回归机的核函数选为径向基核函数“radial”，其余参数选择系统默认值；BP神经网络根据输入向量和输出向量个数，同时结合式(7)选择把隐含层神经元的个数设为6，误差精度设为0.01，最大迭代次数设为2 000，最后经过18次迭代算法成功收敛；遗传算法优化LSSVM把两个参数的寻优范围设为0～600，种群规模设为400，最大迭代次数设为50，基因突变概率设为0.01，最后搜寻出的核函数的参数为7.303 305，正则化参数为454.905 174；最后得到第5～8发弹丸高程y实测值与所有模型预测值如表2高程y所示，关系曲线如图12所示。根据表2计算得到，GM(1,1)模型预测值与实测值的平均相对误差为6.67%，支持向量回归机预测值与实测值的平均相对误差为3.49%，BP神经网络预测值与实测值的平均相对误差为3.62%，遗传算法优化LSSVM预测值与实测值的平均相对误差为3.35%，四个模型构成的组合模型预测值与实测值的平均相对误差为3.25%，组合模型预测精度最高。

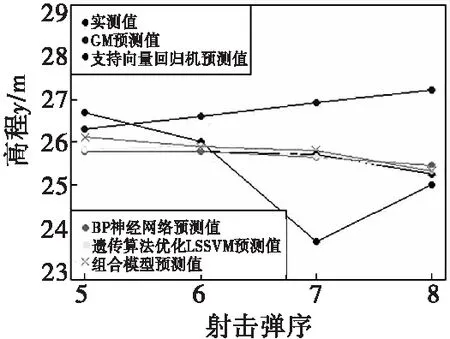
图12 第5～8发弹丸高程y实测值与所有模型预测值关系曲线Fig.12 Relation curve between measured value of projectile elevation y of the 5th to 8th rounds and predicted value of all models

由于所用建模数据量较少，为了证明模型适用于大多数情况，具有一定的通用性，选择把第1～8发弹丸作为训练数据，采用随机选取的方式选取出测试数据。随机选取出的测试数据为第2、5、6、8发弹丸，采用同样的建模预测方法，得到测试数据实测值与各个模型预测值如表3所示。针对射程而言，计算得到GM(1,1)模型预测值与实测值的平均相对误差为0.822%，支持向量回归机预测值与实测值的平均相对误差为0.202%，BP神经网络预测值与实测值的平均相对误差为0.085%，遗传算法优化LSSVM预测值与实测值的平均相对误差为0.076%，四个模型构成的组合模型预测值与实测值的平均相对误差为0.042%；针对横偏而言，计算得到GM(1,1)模型预测值与实测值的平均相对误差为0.777%，支持向量回归机预测值与实测值的平均相对误差为0.547%，BP神经网络预测值与实测值的平均相对误差为0.502%，遗传算法优化LSSVM预测值与实测值的平均相对误差为0.493%，四个模型构成的组合模型预测值与实测值的平均相对误差为0.298%；针对高程y而言，计算得到GM(1,1)模型预测值与实测值的平均相对误差为2.51%，支持向量回归机预测值与实测值的平均相对误差为0.870%，BP神经网络预测值与实测值的平均相对误差为2.7%，遗传算法优化LSSVM预测值与实测值的平均相对误差为0.540%，四个模型构成的组合模型预测值与实测值的平均相对误差为0.383%。可以看出，组合模型的预测精度依然高于所有单项模型，说明在增加样本数据的情况下，组合模型预测精度高于所有单项模型的事实没有改变，说明所采用的方法具有一定的通用性，可以应用于大多数情况。

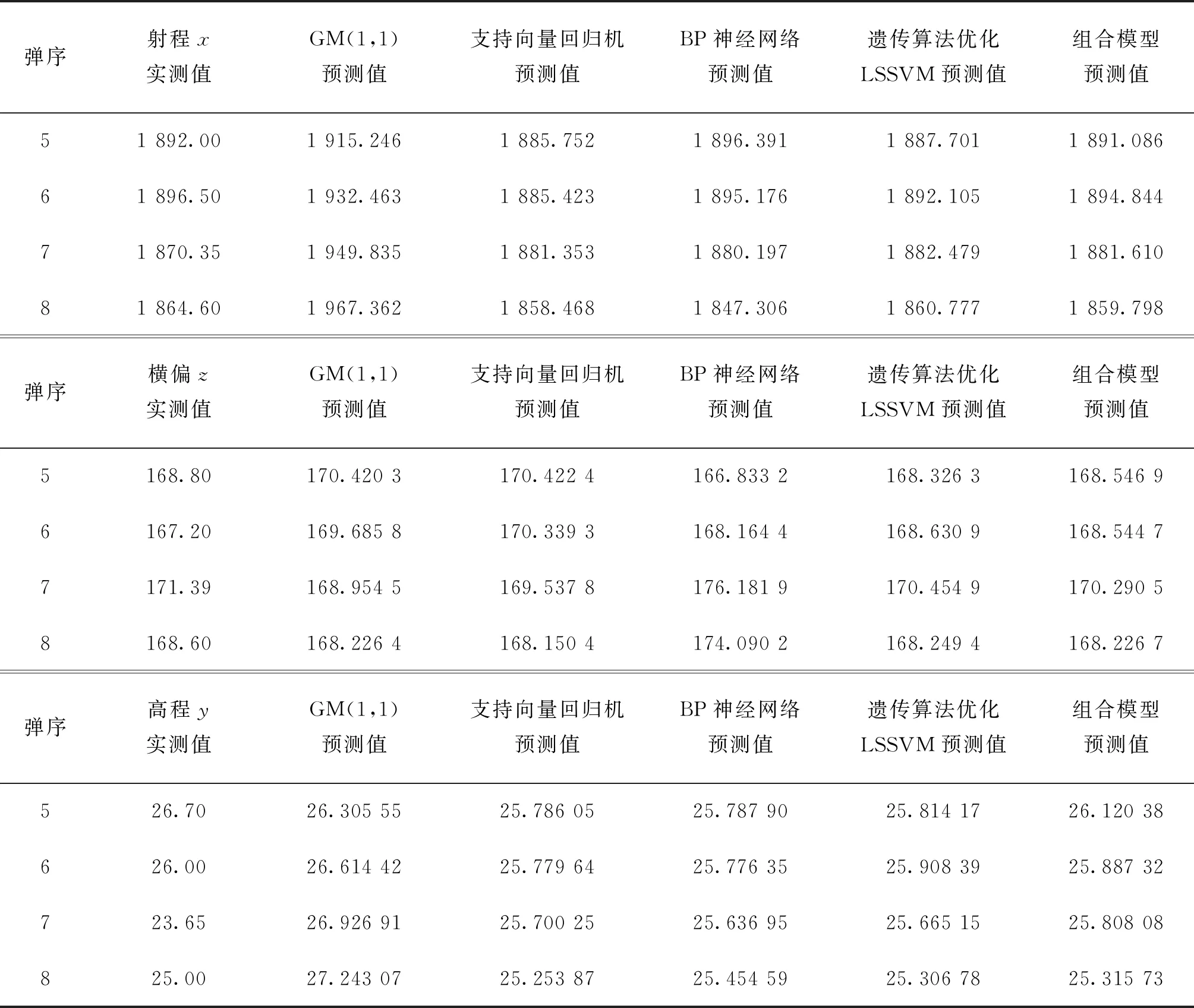
表2 第5～8发弹丸坐标实测值与所有模型预测值Tab.2 Measured values and predicted values of all models of projectile coordinates of the 5th to 8th rounds m

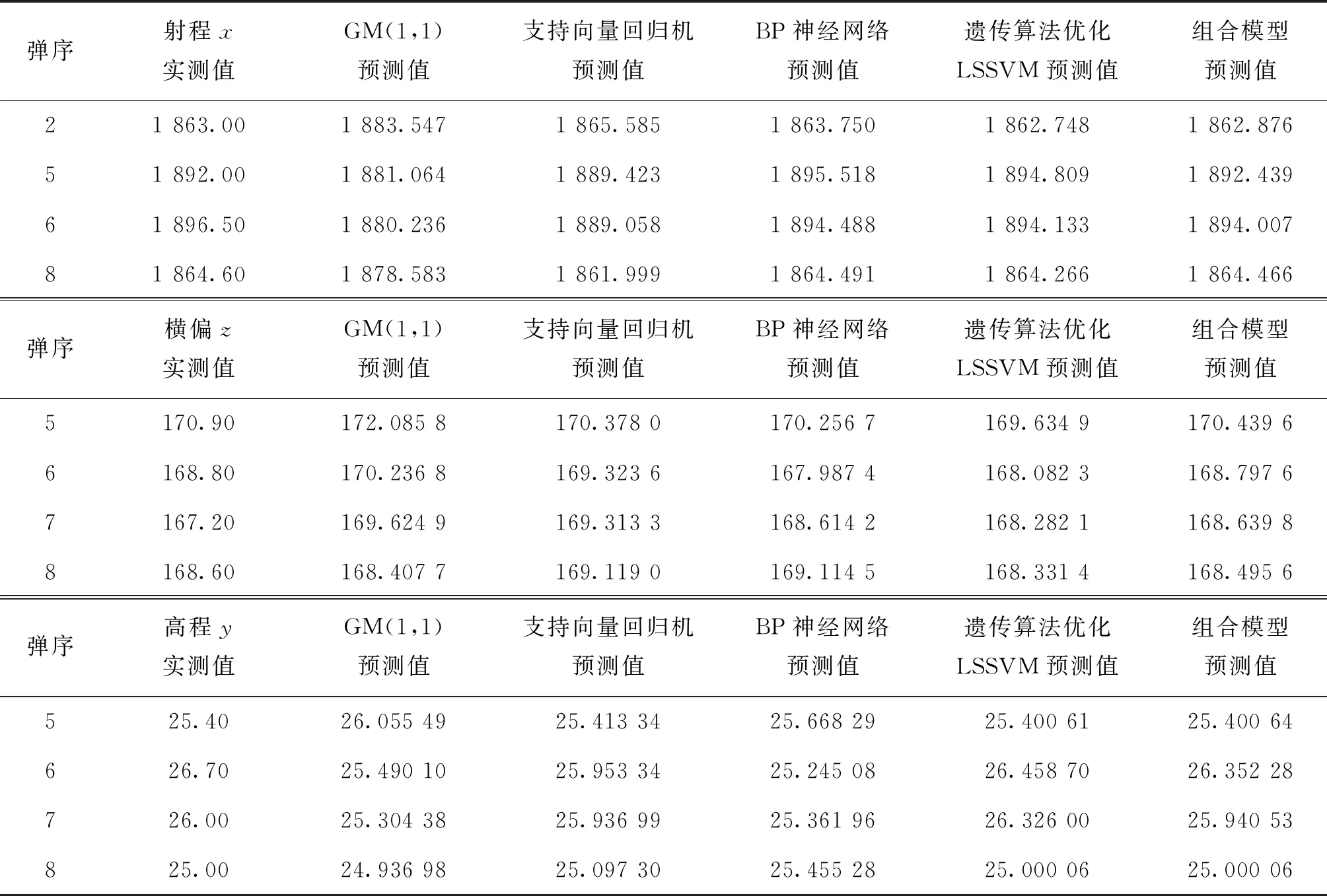
表3 第2、5、6、8发弹丸坐标实测值与所有模型预测值Tab.3 Measured values of the coordinates of the 2nd, 5th, 6th and 8th projectiles and predicted values of all models m

综上所述，对射程x、横偏z和高程y的2次预测结果可知，GM(1,1)模型、支持向量回归机、BP神经网络、遗传算法优化LSSVM构成的组合模型的预测精度高于所有单项模型，说明在弹丸信息未知的情况下，把两台雷达数据进行融合，利用以上模型建立的组合模型可以提高预测弹丸的落点坐标的精度。

4 结论

针对试验中突发情况导致连续波雷达无法准确计算弹丸落点坐标的情况，选择把初速雷达和连续波雷达的数据融合到一起，建立从初速雷达到连续波雷达的支持向量回归机、BP神经网络和遗传算法优化LSSVM等非线性映射模型，同时利用GM(1,1)模型一同预测，最后把四个模型的预测值组合到一起得到组合模型的预测值。试验结果表明，组合模型预测出的弹丸落点坐标更接近实测值，可以作为弹丸落点坐标预测模型。但是该方法还存在一定的研究空间，可采用的数据量还是太少，当数据量非常大时，该方法的普适性和通用性是文章需要进一步研究的方向。