基于图像复原处理的近场MVDR声图测量方法
贺 欢,王逸飞
(1.黄河科技学院信息工程学院,河南 郑州 450000;2.东南大学信息工程学院,江苏 南京 210000)
0 引言
声图测量是一种通过聚焦波束形成方法实现近场精确定位的技术,被广泛应用于空气声学、水声学和医学超声领域的声学成像技术[1-3]。由于自适应聚焦波束形成方法可根据噪声自适应调整阵列各通道加权值,实现信噪比最大输出,其所得声图峰值较为尖锐,空间分辨率较好,被广泛应用于声图测量中[4-7]。但该类方法需要在一定输入信噪比下才能发挥其性能优势,当信噪比较低时,性能变差,甚至使目标空间位置分布估计结果出错[8]。为了降低近场MVDR声图测量中背景级,研究学者提出采用二阶锥凸优化、分子阵处理等方法降低其背景级,但存在如下问题:二阶锥凸优化方法针对切比雪夫滤波方法存在的问题做了进一步改善,可以同步设置波束形成旁瓣级、主瓣宽度等多个指标,实现了波束形成优化,但设置这些参数需要将阵列模型结构一起纳入考虑范围,如果模型结构设置存在问题,将得不到最优结果;分子阵预处理方法在阵列孔径有限情况下,对降低波束形成背景级有限[9-11]。
针对基于最小方差无畸变响应(MVDR)近场声图测量中声图背景级较高问题,本文借鉴图像复原理论中的解卷积技术在阵列信号处理中的应用实例[12-16],提出一种基于图像复原处理的近场MVDR声图测量方法(本文称之为DMVDR方法)。该方法首先根据近场MVDR声图测量方法(本文称之为MVDR方法)输出声图特性,采用类狄利克函数作为声图点扩展函数(point scattering function,PSF);然后利用PSF和R-L方法对MVDR方法输出模糊声图进行解卷积,得到清晰声图估计结果,降低模糊声图背景级及其影响。
1 MVDR方法
1.1 信号模型
如图1所示,在线列阵近场区域,存在K个独立目标,其位置分别为(RK,ΘK)=[(R1,θ1),(R2,θ2),…,(RK,θK)],则线列阵各传感器接收数据可表示为:
X(f)=A(RK,ΘK)S(f)+V(f),
(1)
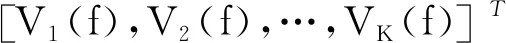

图1 近场声图测量示意图Fig.1 Schematic diagram of near-field source measurement
在近场声传播中,目标声源辐射信号按球面波传播到各传感器位置处,则阵列流形矩阵A(RK,ΘK)具体形式为:

(2)

1.2 MVDR声图测量
针对式(1)所示数据,其协方差矩阵RX(f)可表示为:
RX(f)=X(f)HX(f)=
A(RK,ΘK)HRS(f)A(RK,ΘK)+RV(f),
(3)
式(3)中,RS(f)为目标信号分量协方差矩阵,RV(f)为背景噪声分量协方差矩阵,(·)H为共轭转置。
此时,近场MVDR声图测量最优权向量可表示为:
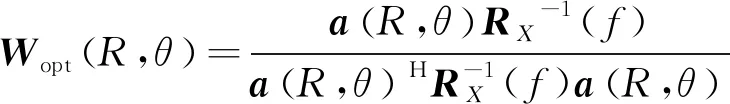
(4)
式(4)中,
为当前扫描点(R,θ)到第n∈[1,N]传感器水平距离,θ为当前扫描点对线列阵法线方向角度,R为当前扫描点相对线列阵中心位置(参考点)距离。
根据获得的权向量最优解,可得到当前扫描点(R,θ)对应的声图测量值。
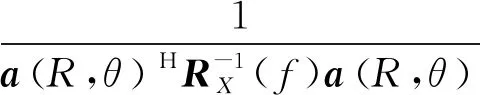
(5)
对协方差矩阵RX(f)进行特征分解,可得:
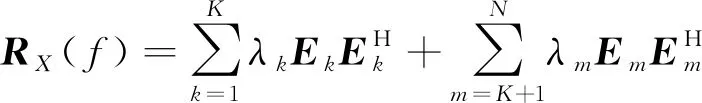
(6)
式(6)中,λk和Ek分别为目标信号分量对应特征值和特征向量,λm和Em分别为背景噪声分量对应特征值和特征向量。
此时,式(5)可分解为:
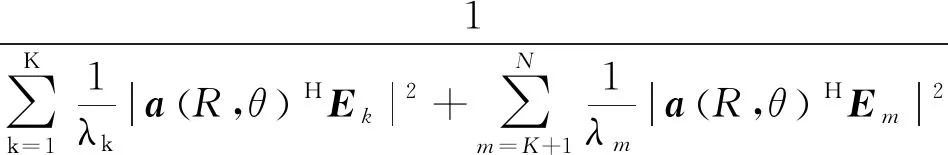
(7)
当扫描点(R,θ)属于空间位置(RK,ΘK),由于Em与a(Rk,θk)正交性,式(7)可简化为:
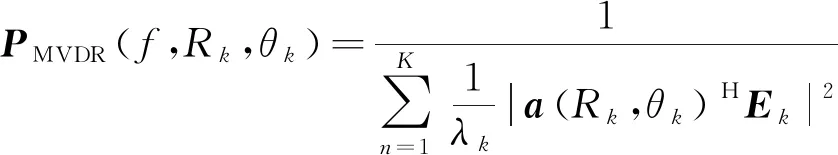
(8)
由式(8)可知,当扫描点(R,θ)属于空间位置(RK,ΘK),MVDR方法具有自动消除噪声分量和保留目标信号分量能力,使信号子空间更好地作用于目标参数估计,理想情况下,MVDR方法声图测量结果具有最优估计效果。
所以,当扫描点到目标声源空间位置时,有R=Rk、θ=θk,此时PMVDR(f,Rk,θk)幅度最大,所以通过搜索最大峰值位置即可实现对目标声源空间位置分布值估计。
2 DMVDR方法
2.1 原理分析
对于空间位置(Rk,θk)处的目标声源,为了后续分析方便,在设定最大扫描距离Rmax上,MVDR方法处理过程可表示为对空间位置(ΔRsinθ,ΔRcosθ)分布值的估计,ΔR=R/Rmax。此时,式(7)可进一步表示为:
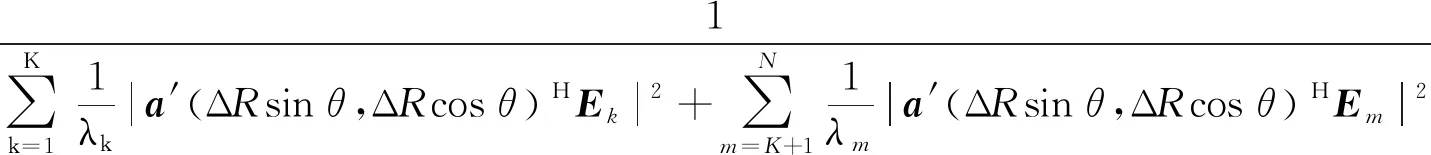
(9)
式(9)中,a′(ΔRsinθ,ΔRcosθ)=[ej2πfτ1′,ej2πfτ2′,…,ej2πfτN′]T,τn′=(Rn-RmaxΔR)/c=τn。
如图1所示,令目标声源在(ΔRsinθ,ΔRcosθ)空间位置分布为Ω,则Ω中的一个元素Ω(ΔRsinθ,ΔRcosθ)可表示为:
Ω(ΔRsinθ,ΔRcosθ)=
Aδ(ΔRsinθ-ΔRksinθk,ΔRcosθ-ΔRkcosθk),
(10)
式(10)中,A为目标声源幅度,δ为二维狄利克函数。
由此可得,MVDR方法所得声图PMVDR(f,ΔRsinθ,ΔRcosθ)可比作是对Ω的估计,即PMVDR(f,ΔRsinθ,ΔRcosθ)可表示为h(ΔRsinθ,ΔRcosθ)与Ω的二维卷积。
PMVDR(f,ΔRsinθ,ΔRcosθ)=
Ω(ΔRsinθ,ΔRcosθ)**h(ΔRsinθ,ΔRcosθ)+V,
(11)
式(11)中,**为二维卷积运算。
由式(11)可知,在已知h(ΔRsinθ,ΔRcosθ)时,可通过解卷积处理,实现对Ω估计,进而获得目标声源空间位置(ΔRsinθ,ΔRcosθ)的估计值[16]。
在目标声源为点源情况时,声图测量方法对目标声源的输出响应可比作为声图探针,即为目标声源在声图上的像,在线列阵有效孔径无限大时,探针在目标声源位置处的理想响应为一个二维狄利克函数[16]。因此,可利用一个“类狄利克函数”构造声图PMVDR(f,ΔRsinθ,ΔRcosθ)的点扩展函数,即
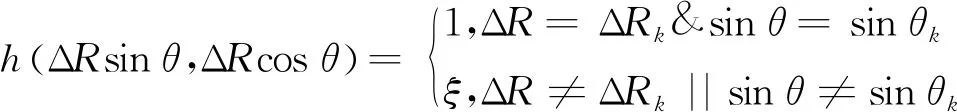
(12)
式(12)中,ξ∈(0,1)的常数。
将式(9)中,声图PMVDR(f,ΔRsinθ,ΔRcosθ)表示成二维卷积形式为:
PMVDR(f,ΔRsinθ,ΔRcosθ)=
Π(ΔRsinθ,ΔRcosθ)**h(ΔRsinθ,ΔRcosθ)+V,
(13)
式(13)中,Π(ΔRsinθ,ΔRcosθ)表达式为:
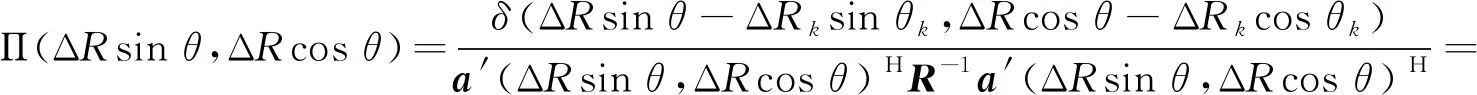
(14)
2.2 声图复原
针对MVDR方法输出声图PMVDR(f,ΔRsinθ,ΔRcosθ)中背景级较高的问题,本文利用Richardson-Lucy方法[15-16]对式(13)进行二维解卷积,估计Π(ΔRsinθ,ΔRcosθ)。
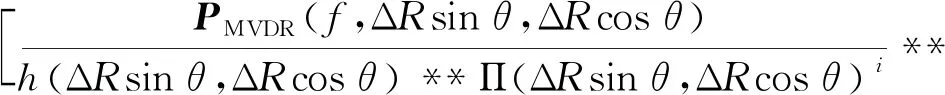
(15)
采用式(15)进行迭代时,ξ取为归一化声图平均值,即为:
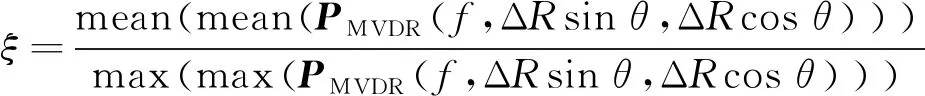
(16)
式(16)中,mean(·)为均值运算符, max(·)为最大值运算符,在均值求取时将最大值周围值置零。
式(15)处理后的声图可表示为:
PDMVDR(f,ΔRsinθ,ΔRcosθ)=Π(ΔRsinθ,ΔRcosθ)I。
(17)
3 数值仿真分析
为了验证本文方法的可行性和有效性,仿真中线列阵由32个传感器组成,相邻传感器间距为4 m,采样率为5 kHz,一次处理数据总量为5 kB。接下来采用常规聚焦波束形成方法(CBF方法)、MVDR方法、文献[11]方法和DMVDR方法进行对比分析。
3.1 单目标声源情况
仿真中,假定目标声源相对线列阵为点源,目标声源位于相对线列阵阵中心(80 m,0°)位置处,目标声源辐射频率为[160 Hz,200 Hz]宽带信号,背景噪声为高斯白噪声,各传感器拾取数据所含信噪比为SNR。仿真扫描平面为水平距离[20 m,200 m]、方位角度[-90°,90°],将该区域按扫描网格划分,网格间距为2 m,角度1°。
图2—图4分别给出了4种方法在SNR=-5,-10,-15 dB情况下所得距离R=80 m处不同角度下声图测量值。
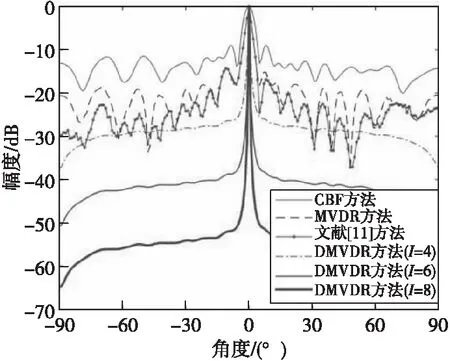
图2 4种方法所得声图测量值(SNR=-5 dB)Fig.2 One-dimensional source distribution map of four methods(SNR=-5 dB)
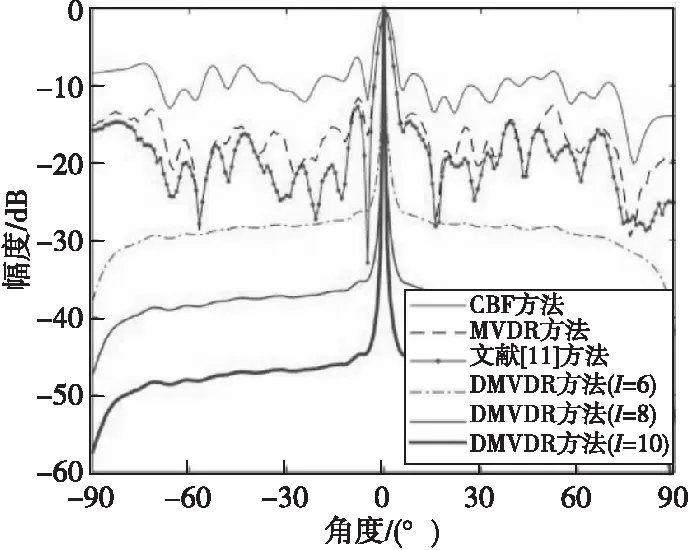
图3 4种方法所得声图测量值(SNR=-10 dB)Fig.3 One-dimensional source distribution map of four methods(SNR=-10 dB)
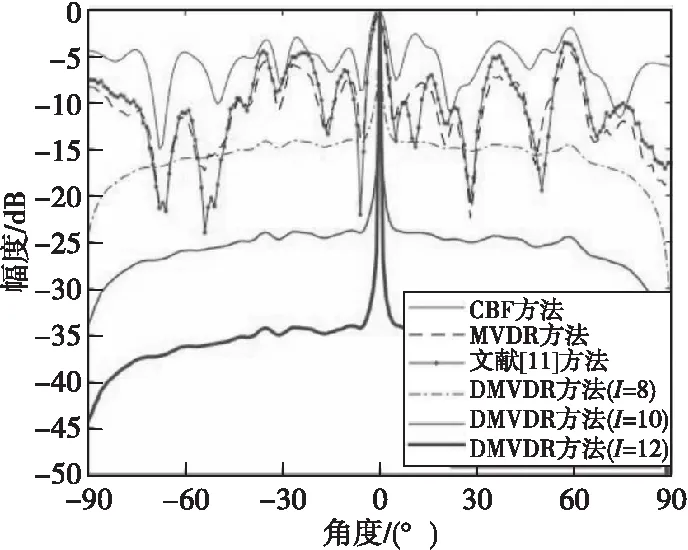
图4 4种方法所得声图测量值(SNR=-15 dB)Fig.4 One-dimensional source distribution map of four methods(SNR=-15 dB)
由图2—图4结果可得:当SNR=-5、SNR=-10、-15 dB时,不同方法输出背景级如表1所示。
由表1可知:MVDR方法通过约束目标位置处信号功率不变,噪声和非目标位置处功率最小,相比CBF方法,降低了声图背景噪声级;文献[11]方法通过分子阵处理,在高信噪比下降低了声图背景级,但在低信噪比下相比MVDR方法改善效果有限;而DMVDR方法通过4次迭代解卷积即可实现优于MVDR方法的效果,且随着I变大,其输出背景级降低越大,背景更平滑,远低于CBF方法、MVDR方法和文献[11]方法,具有更优的目标位置估计能力。
另外,DMVDR方法相比MVDR方法,在仿真中进行解卷积运算,该方法增加了I×R×(2Θ2+Θ)乘法和I×R×Θ2加法运算,R为声图扫描距离个数算法复杂度增加了,Θ声图扫描角度个数,算法复杂度增加。采用 Inter Corei7 2核处理器,在Matlab2019a编程环境下,进行1次处理DMVDR方法所需运算时间为0.312 2 s(I=12),由此可见,DMVDR方法可满足实际应用中的实时性要求。
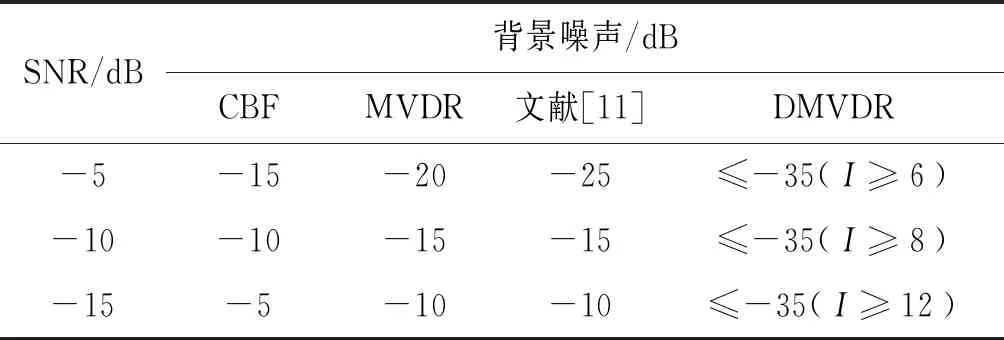
表1 不同方法输出背景级Tab.1 The output ground level of different methods
3.2 双目标声源情况
采用两个目标声源对DMVDR方法有效性进行分析论证。仿真中,假定目标声源相对线列阵为点源,两目标声源位于相对线列阵阵中心(80 m,-2°)和(80 m,2°)位置处,目标声源辐射频率为[160 Hz,200 Hz]宽带信号,背景噪声为高斯白噪声,各传感器拾取数据所含信噪比为SNR。仿真扫描平面为水平距离[20 m,200 m]、方位角度[-90°,90°],将该区域按扫描网格划分,网格间距为2 m,角度1°。
图 5—图 8分别给出了4种方法在SNR=-10 dB情况下所得声图;图9给出了4种方法在SNR=-10 dB情况下所得距离R=80 m处不同角度下声图测量值。
由图5—图9显示结果可得不同方法输出最大旁瓣级如表2所示。
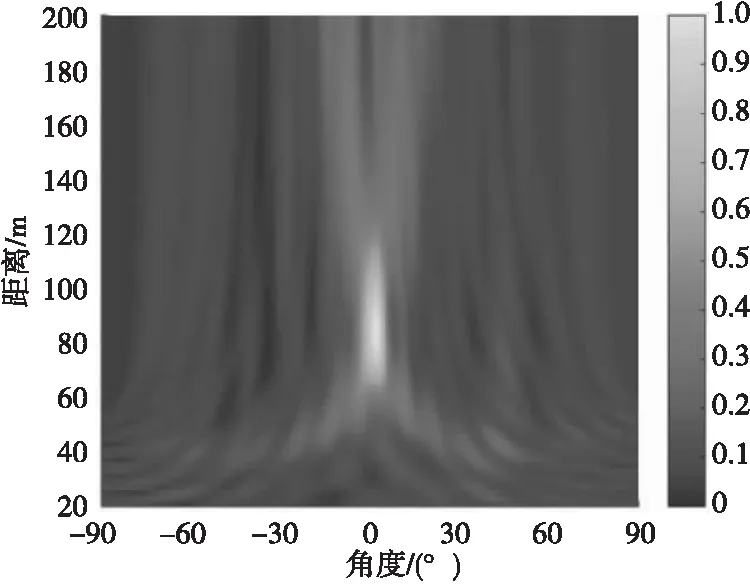
图5 CBF方法所得声图Fig.5 Two-dimensional source distribution map of CBF method
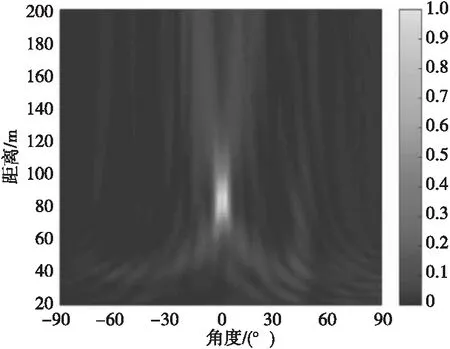
图6 MVDR方法所得声图Fig.6 Two-dimensional source distribution map of MVDR method
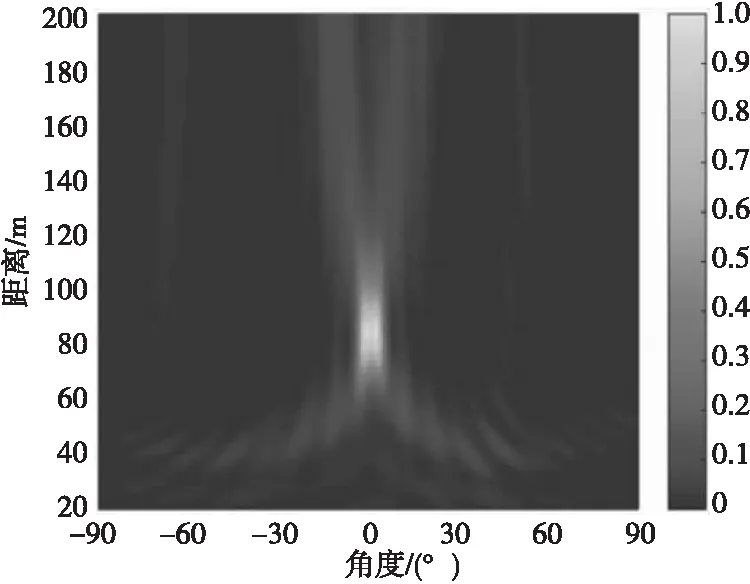
图7 文献[11]方法所得声图Fig.7 Two-dimensional source distribution map of Ref.11 method
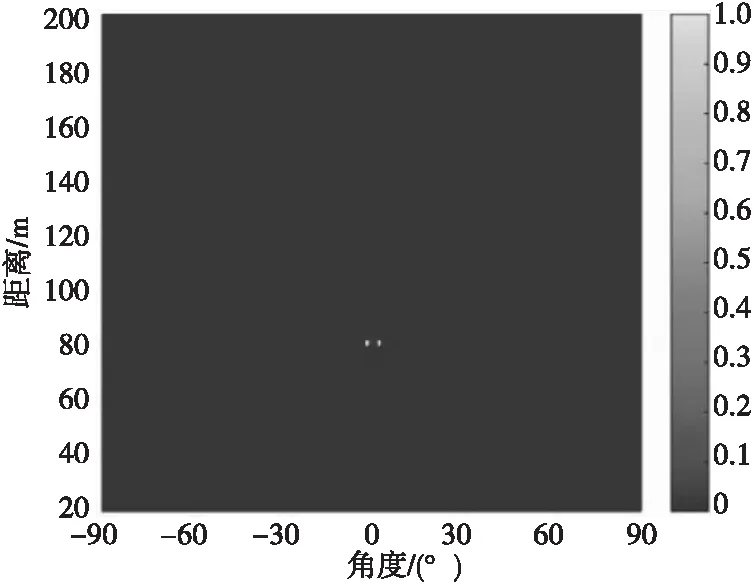
图8 DMVDR方法所得二维声图 (I=6)Fig.8 Two-dimensional source distribution map of DMVDR method(I=6)

表2 不同方法输出最大旁瓣级Tab.2 The output max side valve of different methods
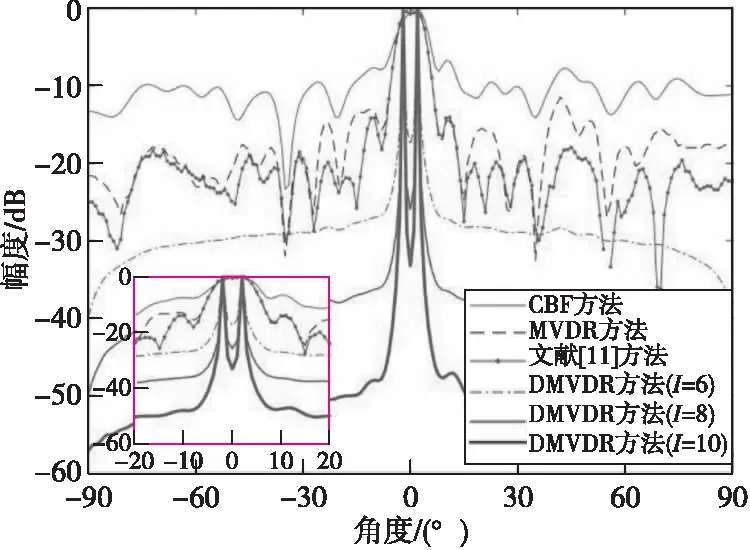
图9 4种方法所得一维声图Fig.9 One-dimensional source distribution map of four methods
由表2可知:DMVDR方法输出最大旁瓣级变化趋势与其输出背景级一致,随着I变大,其输出最大旁瓣级降低越大,进一步说明该方法降低的旁瓣级可使其背景更为光滑,目标显示更为清晰,可降低对其他目标的影响,便于真实目位置提取。
不同方法输出聚焦峰尺度如表3所示。

表3 不同方法输出聚焦峰尺度Tab.3 The output focus peak scales of different methods
由表3可知:CBF方法受“瑞利限”限制,所得声图聚焦峰尺度较大,分辨能力较差,当两目标声源较近时产生混叠现象;MVDR方法和文献[11]方法通过对目标和非目标进行约束处理,降低了聚焦峰尺度,目标位置分辨率得到提高,减小了“混叠”影响,能够分辨出两个目标空间位置,但显示清晰度有限;而DMVDR方法通过多次迭代解卷积运算即可实现优于MVDR方法和文献[11]方法的效果,且随着I变大,其输出峰值更“尖锐”,聚焦峰尺度越小,目标位置分辨率越好,能够更清晰地显示出两目标声源位置。该结果进一步说明DMVDR方法输出声图继承了MVDR方法的高分辨估计性能,能更优地估计出目标位置。
4 结论
针对最小方差无畸变响应声图测量方法输出声图背景级较高问题,本文提出一种基于图像复原处理的近场MVDR声图测量方法——DMVDR方法。DMVDR方法通过MVDR方法输出声图所包含的信息对其处理中的点扩展函数实现设计,并基于图像复原理论中解卷积技术实现对MVDR方法输出声图进行解卷积,减少了背景级对其输出结果的影响,对目标声源实现了空间位置分布估计。数值仿真结果表明:DMVDR方法通过解卷积迭代处理有效降低了声图背景级,使其低于CBF方法、MVDR方法、文献[11]方法输出声图背景级,背景更加平滑,声图峰值更加“尖锐”,显示效果清晰可辨,并具有与MVDR方法一致的目标声源空间位置高分辨估计能力和空间位置分布估计能力。

