基于改进蝙蝠算法的水下机器人避障路径优化方法

龚成勇，刘 康，曾永亮

(1.兰州理工大学能源与动力工程学院，甘肃 兰州 730050;2.兰州理工大学黄河流域水生态与水工程研究院，甘肃 兰州 730050)

0 引言

智能机器人广泛运用于农业生产、航天科技、材料加工、医疗救援等领域。目前全国已建成的各类型水库总数量为98 795座，总库容为9 035亿m3[1]，受常年使用老化以及地质灾害影响，水下部分存在隆起、冲刷、淘空、错位、脱落、塌陷 、腐蚀、侵蚀、剥蚀、破损、蜂窝、麻面、露筋、滑坡、裂缝、渗漏、管涌、流土等安全隐患及险情。目前常用的排查方法主要有潜水员进行人工下水排查，或远程操纵机器下水排查。人工排查难度大、危险性高，具备自主巡航、自主作业、自行返回等功能的智能型水下机器人备受青睐，其特点是高灵活性、长作业时间、广作业区域，因此水下机器人成为水库等地的隐患排查工具和手段。而自主避障能力是水下机器人在路径规划中最为突出重要的一项能力，这要求智能机器人有对障碍物的自行规避与从起点到终点的路径规划的能力。路径规划问题的实现算法分为传统算法与智能算法，传统算法有模糊算法、可视图、自由空间法、人工势场法等。模糊控制算法求解多维问题难以建立模糊规则库[2]；可视图法实时性能较差，且效率较低[3]；自由空间法处理复杂障碍空间，其复杂度将超出计算能力范围[4]；人工势场法易得局部最优而难以到达终点[5]。随着人工智能的崛起，智能仿生算法被应用于路径规划与优化问题，如PSO算法(particle swarm optimization，PSO)[6]、人工鱼群算法[7]、蚁群算法[8]等。传统PSO中粒子易陷入不良区域，种群多样性不足，搜索停滞，后期收敛速度较差[9]；基本鱼群算法的历史行为学习度不足，收敛精度低[10]；基本蚁群算法信息浓度低，搜索速度慢[11]。

近年来又出现了一种新型智能优化算法即蝙蝠算法(bat algorithm，BA)，是模拟蝙蝠捕食飞行过程的一种仿生智能算法，具有模型简单、算法参数少，有并行性强且分布式广的特点[12]；但由于初期搜索范围不够广，收敛过快，精度较低，后期存在较多停留边界的个体，种群多样性差等问题。

因此本文将其与高斯函数与柯西函数结合，引入高斯柯西变异策略，帮助算法逃离局部极值的同时提高算法精度。另外使用线性渐变法调节响度和脉冲发射率，通过脉冲发射率的大小调节全局与局部搜索的关系，进一步优化收敛速度。针对存在的个体飞出解空间边界导致收敛速度慢的问题，采用边界再分配机制，减少个体在边界聚集、提高优化效率。

1 基本蝙蝠算法

蝙蝠算法是通过数学的方法，以蝙蝠回声定位飞行为基础，构造出相关模型以期解决一些复杂问题的一种智能算法。模型主要通过相关变量代替蝙蝠飞行时特定的频率和响度的声波，去寻找发现当前最优解。记f(x)为目标函数，每只蝙蝠在算法中都有相应的函数值，代表一个可行解，通过函数值比较判断出最优个体。算法的迭代可分解成四个过程：

1) 随机飞行

fi=fmin+(fmax-fmin)β，

(1)

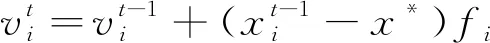
(2)

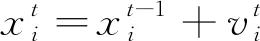
(3)

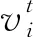
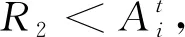
2) 局部搜索。蝙蝠接近全局最优解时,再引入一个取值在0至1的均匀分布数R1，若R1>r1，则开始局部搜索，否则继续全局搜索。通过下式更新位置：

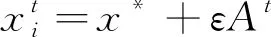
(4)

式(4)中，ε为[-1,1]上的均匀分布随机数，At是第t代所有蝙蝠响度的平均值。

4) 更新参数。接受新解意味着蝙蝠在靠近猎物，响度减小的同时，脉冲发射速率ri不断增加。其更新公式如下：

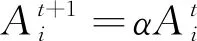
(5)

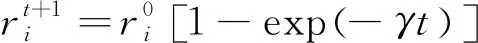
(6)

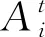
2 蝙蝠算法的改进与实现

2.1 高斯柯西变异

单一的高斯变异或柯西变异并不能完美地利用其分布特性。从函数图来看，柯西分布两侧高，产生的随机数范围相对更广，可扩大飞行区域，避免个体的聚集导致取得局部极小。

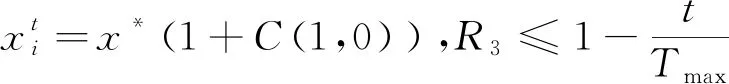
(7)

式(7)中，R3是个随机数，服从均匀分布，t为迭代次数，Tmax是最大迭代次数，C(1,0)是服从标准柯西分布的随机变量。

高斯分布具有中心附近概率较高的特性，从图1来看，产生的随机数相对集中，适合精细搜索，更容易寻到最优解。

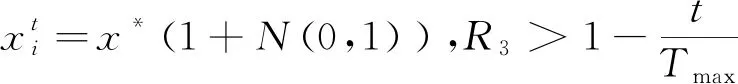
(8)

式(8)中，R3∈(0,1)是个均匀分布随机数，N(0,1)是服从标准高斯分布的随机变量。

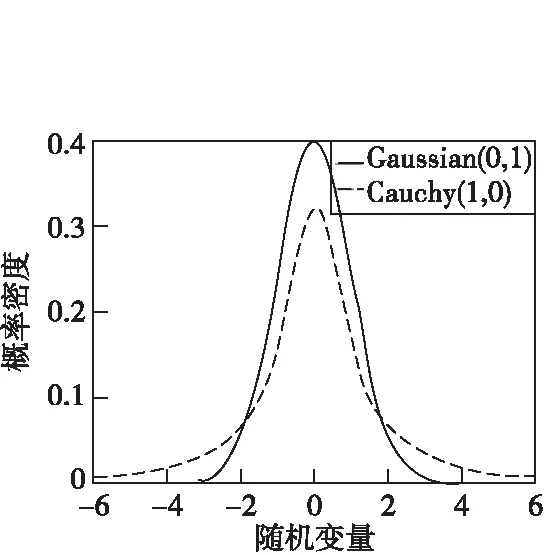
图1 柯西与高斯概率密度Fig.1 Probability density of Cauchy and Gaussian

2.2 线性渐变算法

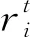
(9)

由于两个参数单调递减，故响度最大值Amax即初始响度，一直递减至最小值Amin，脉冲发射率rmax即初始脉冲发射率一直递减至最小值rmin，直到达到最大迭代次数Tmax。

2.3 界限随机重置机制

由于蝙蝠算法随机搜索的内生性，个体搜索至边界后聚集不可避免，这将进一步降低多样性。为此本文融合界限随机重置机制，将越界个体进行位置随机重分配，而保证个体的速度大小和方向不改变，以此提高个体利用，加快算法后期收敛。位置更新如下式所示：

X*=bL+λ(bU-bL)，

(10)

式(10)中，λ∈[0,1]是一个随机变量，是位置随机分配因子；bL代表空间边界的下界，bU代表空间边界的上界。

2.4 算法实现流程

本文算法的实现具体流程如下：

1) 建立地图环境，确定出发点与目的点，限制迭代次数，初始化蝙蝠位置、速度、频率、脉冲发射频率、响度、种群规模等参数。

2) 计算蝙蝠种群的适应度，记录最优个体x*。

3) 按照式(2)、式(3)更新蝙蝠位置和速度，越界个体按式(10)进行处理,产生新个体xnew。

4) 生成随机数R1，若R1>ri，则根据式(7)、式(8)选择变异机制，并将变异个体赋值给xnew。

6) 比较所有蝙蝠的适应度，找到当前最优解x*。

7) 重复步骤3)步骤6)，直到达到最大迭代次数。

8) 得到最佳路径。

3 水下机器人避障及仿真

3.1 环境建立

本文以数学模型模拟真实的水下三维环境，主要研究复杂水下地形的水下机器人全局路径规划问题。以山峰的形式模拟机器人水下工作面临的地形状况，由于水下机器人需要贴近水底对相关设施进行排查作业，故仿真时使得机器人尽可能贴近水底作业而不至于触碰障碍物。将机器人实际工作环境用三维的水下地形和俯视角度的等高线图形表示，如图2、图3所示。整个模型空间为200 m×200 m×200 m，x范围是(0，200) m，y为(-100，100) m，z为(-450，-250) m。

3.2 参数设置

为验证改进后算法在水下机器人全局路径规划问题中是否具备优越性，以Matlab R2016a软件为基础，将算法思路进行一系列仿真实验。为模拟复杂环境的规划问题，解空间并未设置标准正方体，水下机器人的起点坐标设为(0，-100，-350) m，目标点设为(200，100，-360) m，水下机器人体积忽略不计，视为空间中的质点。算法的基本参数设置如表1所示。

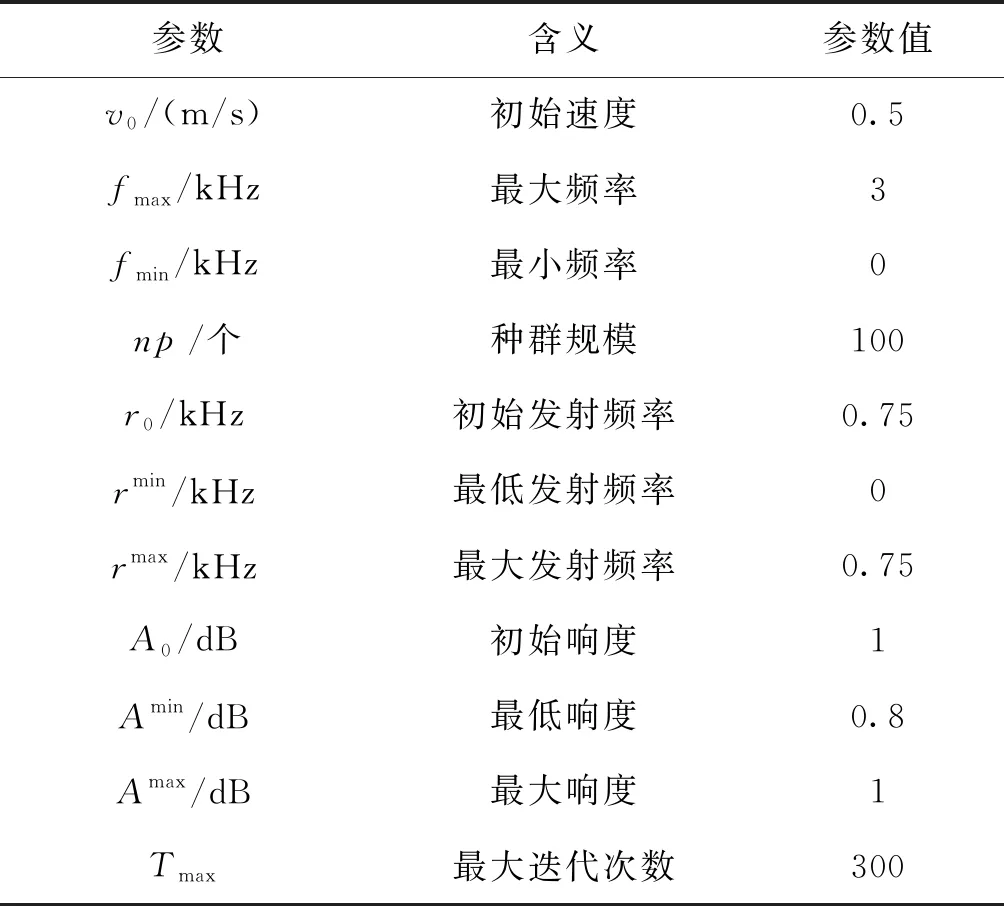
表1 模拟基本参数Tab.1 Basic parameters for simulation on planned path

3.3 实例数值模拟

基于相同环境且根据上节设置的参数值，分别利用本文算法和基本蝙蝠算法进行路径规划，并分别与文献[12]中的GHBA和VWBA算法进行对比，模拟结果图3为改进前的三维规划路径，图4为改进前的规划路径俯视栅格图，图5为改进后的三维规划路径，图6为改进后的规划路径俯视栅格图。

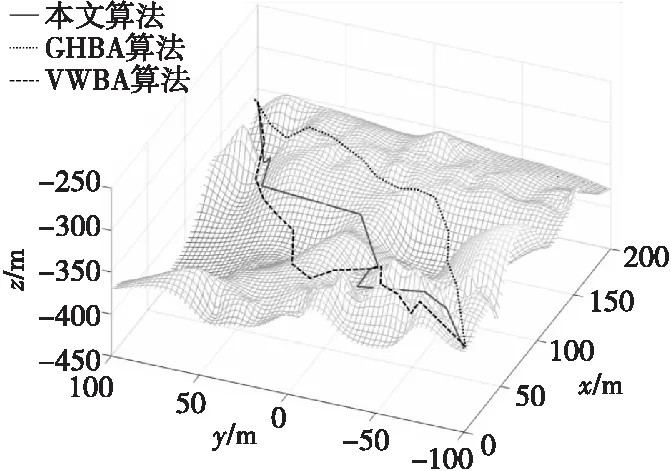
图3 算法改进前规划路径Fig.3 Planned path based on bat algorithm before improved

从图3、图5与图4、图6对比可以看出，相比于基本蝙蝠算法，本文算法规划出的路径长度短，节点数少，且没有急剧的锐角转弯，路径的平滑性更好，符合机器人实际运行要求。因此在对机器人进行路径规划时，本文算法能够更好地适应机器人实际运行环境，高效完成相应任务，对机器人的工作更加有利。而基本蝙蝠算法容易出现往复的无用规划，且存在较多易损伤机器人物理结构的锐角机动。另外，本文算法到达目标点所需的算法收敛时间明显少于基本蝙蝠算法，表明本文算法的收敛效果优于基本蝙蝠算法，规划效率更加高效。具体的指标对比如表2所示。

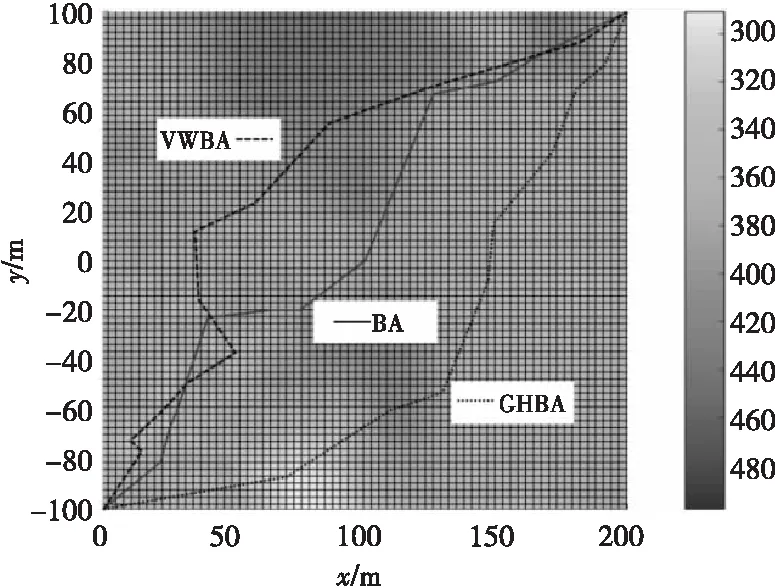
图4 改进前规划路径俯视栅格图Fig.4 The top-view grid map of planned path based on bat algorithm before improved

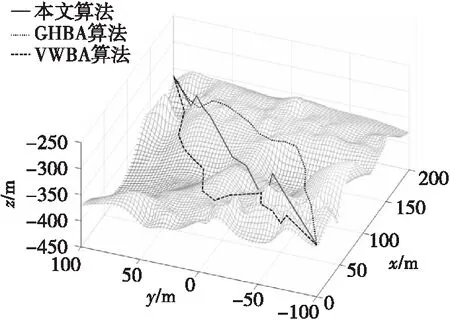
图5 算法改进后规划路径Fig.5 Planned path based on improved bat algorithm

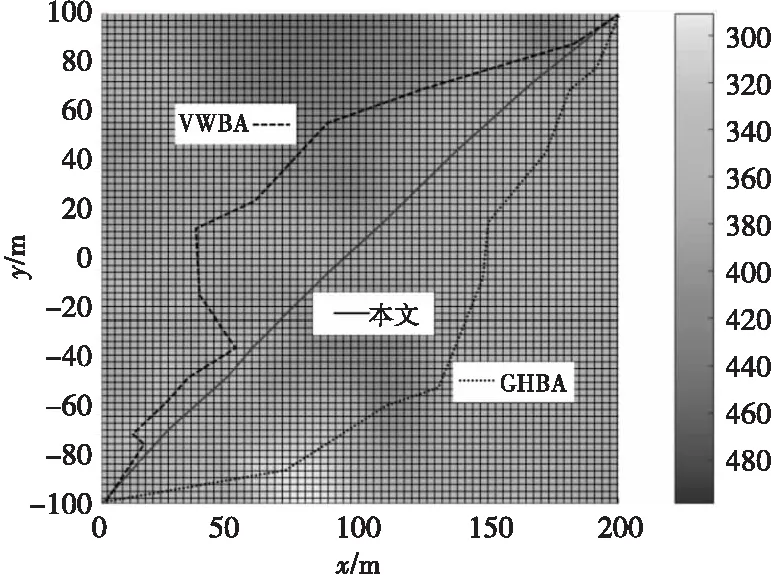
图6 改进后规划路径俯视栅格图Fig.6 The top-view grid map of planned path based on improved bat algorithm

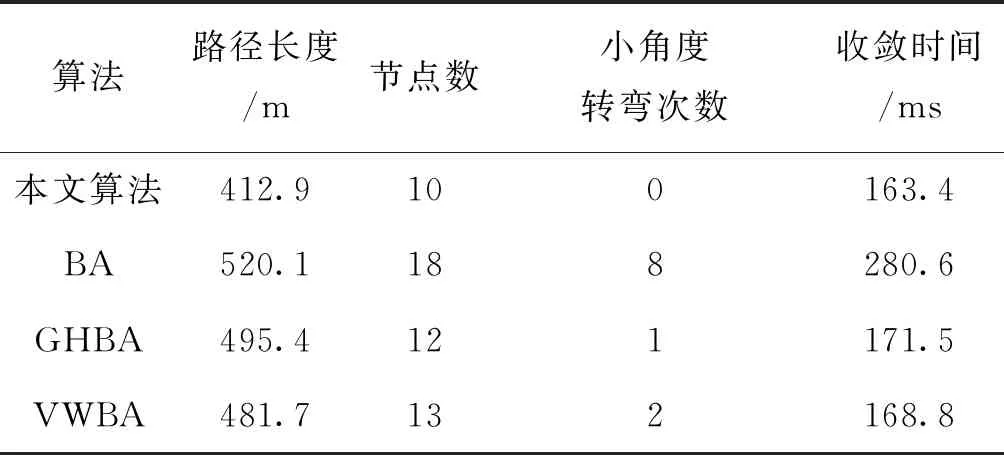
表2 指标对比Tab.2 Comparison to indicators of simulation on path planning based on different algorithms

4 结论

针对水库中水下机器人避障研究过程中出现的问题，通过研究改进蝙蝠算法，主要可以得到以下结论：1) 使用线性渐变法调节响度和脉冲发射率，通过脉冲发射率的大小调节全局与局部搜索的关系，进一步优化收敛速度，从而提高机器人的路径定位速度。2) 在局部寻优阶段融合高斯柯西变异策略，前期利用柯西函数两翼高概率特性产生广泛围随机数，扩大算法搜索范围，后期利用高斯函数中间概率高、两端概率低的特性进行精准定位。保证机器人全局最优路径规划同时，提高了局部精度。3) 采用界限随机重置机制，优化了蝙蝠在边界聚集，带来的种群多样性不足问题，提高收敛效率。满足了机器人实际定位有效性。

数值模拟表明，改进后的算法规划路径更短，拐点数更少，运行时间短，迭代次数少，对水下机器人工作运行过程中的避障能力更强，路径规划平顺且长度短，为现实机器人智能避障提供了一种优化方法。