基于虚拟透镜成像技术的转台ISAR成像方法

张继龙，王 栋，张继康

(1.苏州威陌电子信息科技有限公司, 江苏 苏州 215312；2.中企基业(北京)管理顾问有限公司，北京 100039；3.北京敏视达雷达有限公司，北京 100094)

0 引言

在雷达技术基础上进一步发展起来的合成孔径雷达(synthetic aperture radar，SAR)[1-6]、逆合成孔径雷达(inverse synthetic aperture radar，ISAR)[7-13]等技术近年来得到大量应用。其中SAR雷达通常位于运动平台上，通过平台运动在空间合成等效大口径阵列而获得更高的探测精度。而ISAR雷达则通常固定不动，通过目标的空间运动获得等效的大口径阵列来提高探测精度。在这两种技术体制中，都需要目标与雷达平台之间存在不同的相对运动以产生差异化的多普勒频移，从而实现对目标的高精度探测。但由于实际雷达运载平台或目标的运动都较为复杂，因而需要进行非常复杂的运动补偿才能实现精确探测和成像。

虚拟透镜成像技术[14-18]是一种成像新技术，即通过模拟透镜成像机制，对阵列单元信号进行复加权运算，计算出预期成像平面上目标的像。文献[14]首次提出了基于透镜成像原理的微波阵列成像新思路，文献[15]分析了成像特性，文献[16]提出了一种快速成像算法提高了成像速度，文献[17—18]解决了像场坐标修正等系列问题。虚拟透镜成像技术具有算法简洁高效、体制兼容性好的优点。本文在上述研究的基础上，将该技术拓展到主动ISAR成像领域，提出一种ISAR转台成像新方法。该方法不依赖于目标回波的多普勒频移，能够实现对转台目标的高效成像。此外，本文所述方法同样适用于圆柱扫描成像系统，也适用于柱面扫描合成孔径雷达成像。

1 虚拟透镜成像的基本原理

虚拟透镜成像技术的基本原理如图1所示，对天线单元接收到的目标散射信号移相后进行球面波二次散射，进而计算出在预定的成像平面上的合成像。

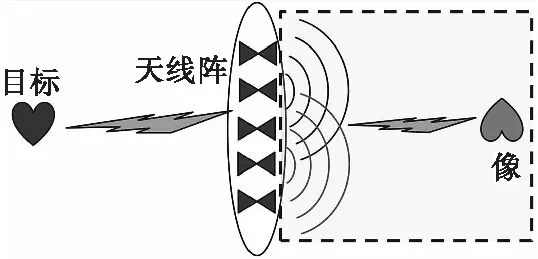
图1 虚拟透镜成像原理示意图Fig.1 Schematic diagram of virtual lens imaging principle

文献[17]给出了等效透镜单元的移相量简化计算公式及成像快速算法，其中移相量简化计算公式为：

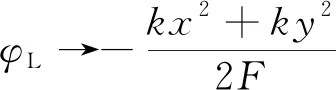
(1)

式(1)中，φL为阵列单元的透镜相移，k为波数，(x,y)为天线单元坐标，F为焦距。

像场的快速计算公式为：

Eq=IFFT(E·A·ejφF)，

(2)

式(2)中，Eq为目标的像，E为阵列单元接收到的目标散射信号，A为阵列单元的幅度加权系数，φF为聚焦相位加权系数，符号IFFT代表二维快速傅里叶逆变换(IFFT)。

聚焦相位加权系数φF的计算公式如下：

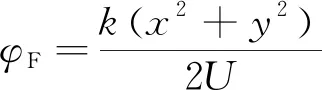
(3)

式(3)中，U为物距，即目标所在平面到阵列所在平面的距离。

2 新转台成像系统的特性

在传统ISAR成像方法中，需要目标部件与雷达平台之间存在不同的相对运动以获得不同的多普勒频移。将虚拟透镜成像技术应用于ISAR成像，能够实现不依赖于多普勒频移的自聚焦成像。但现有虚拟透镜成像技术是基于平面阵列天线，并且仅适用于被动式或半主动式成像，需要针对ISAR成像进行适应性改进。

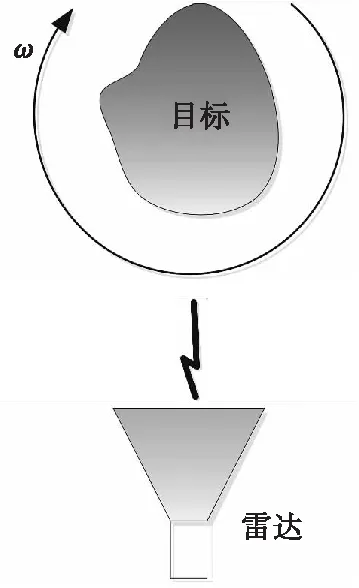
图2 转台成像示意图Fig.2 Diagram of turntable imaging

在图2所示转台成像系统中，当探测雷达采用平行于转动轴的一维线阵时，由于目标与探测雷达之间的相对运动，成像系统会形成圆柱面的空间合成阵面。在此圆柱面阵面探测系统中，目标散射信号传输到阵列单元，阵列单元收到信号进行移相后，以球面波的形式进行二次散射，信号传播路径如图3所示。

信号经过不同的传输路径R1、R2到达成像平面处，在不考虑传播衰减的情况下，目标的像可用公式表示为[17]：

Eq(δ,σ)=Ep(ζ,ξ)∬e-j(φ1+φL+φ2)dxdy,

(4)

式(4)中，Eq(δ,σ)为目标的像，Ep(ζ,ξ)为目标的散射信号，φ1为散射源P到阵列单元的单程传播相移，φ2为阵列单元到像点Q处的单程传播相移，φL为阵列单元的透镜相移。

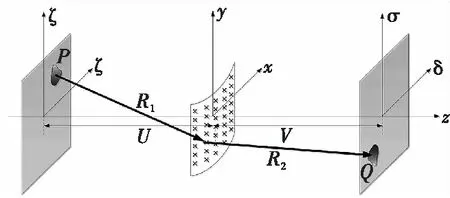
图3 柱面成像示意图及其坐标系Fig.3 Diagram of cylindrical imaging and its coordinate system

在柱坐标系下，假设目标位于柱面的轴线附近，柱面半径为ρ,φ表示柱坐标系下，阵列单元偏离阵列中心的角度。(x,y,z)表示阵列单元的坐标，(ζ,ξ,-U)为散射源坐标，(δ,σ,V)为像点坐标；U为物距，即目标平面到阵列平面的距离；V为像距，即成像平面到阵列平面的距离；随着扫描位置的变化，阵列单元的坐标存在如下关系式：

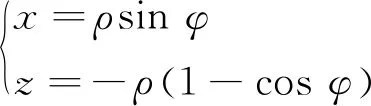
(5)

从而有：

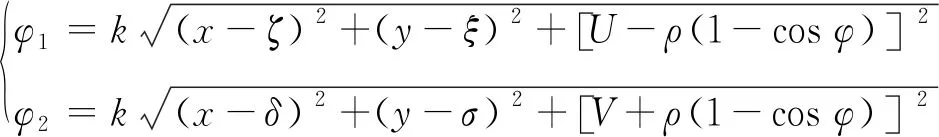
(6)

式(6)中，k为波数。

将式(6)级数展开并忽略高次项有：

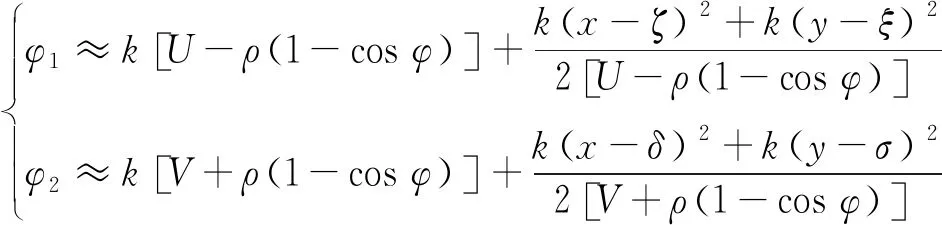
(7)

一般情况下，有U≫ρ(1-cosφ)、V≫ρ(1-cosφ)，从而式(7)可以进一步近似为：

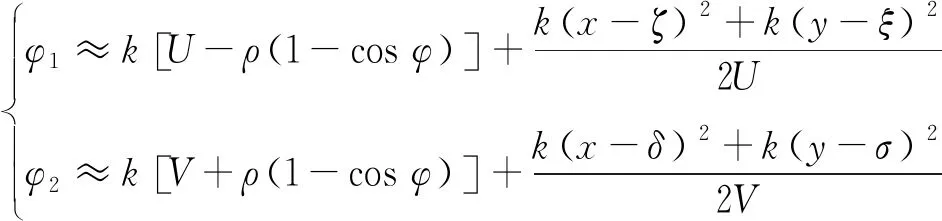
(8)

若仅考虑对成像有帮助的坐标相关变化分量，由式(8)还可以进一步得出成像有效相移为：

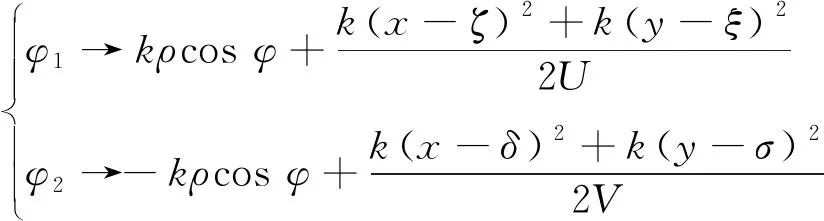
(9)

将式(1)、式(9)代入式(4)化简整理可得：

Eq(δ,σ)=Ep(ζ,ξ)e-jψ1∬e-jψ2ejωδxejωσydxdy，

(10)

式(10)中，

Eq(δ,σ)=Ep(ζ,ξ)·e-jψ1·∬ejωδxejωσydxdy。

(11)

研究表明，阵面规模越大，式(11)右边的二重积分结果越接近狄拉克函数(Dirac)的形态，此时所获得的像与源场之间存在如下近似线性关系[17]:

(12)

通过分析同样可以证明，虚拟透镜成像技术也适用于主动式转台成像系统。主动ISAR转台成像系统中，在合成的虚拟柱面孔径上，阵列单元依次发射和接收目标的反射信号，此时探测信号从天线单元发出，到目标反射后再被天线单元所接收，信号经历了R1的双程传输，对应的相位延迟为2φ1。在这种情况下，成像处理时则需要对透镜单元相移、φ2传播相移都作双程处理。在不考虑传播衰减的情况下，目标的像同样可用公式表示为：

Eq(δ,σ)=Ep(ζ,ξ)∬e-2j(φ1+φL+φ2)dxdy。

(13)

采用上述相似的推导过程，可证明式(12)同样适用于主动式转台成像系统。

由上述分析可知，虚拟透镜成像技术可用于转台成像系统，且所成的像与源之间存在良好的近似线性关系，并且该成像方法可不依赖于多普勒频移。

3 转台ISAR成像快速算法

前面已经证明虚拟透镜成像技术可用于转台ISAR成像，下面将给出成像算法的实现模型。

由于实际合成的虚拟柱面通常为离散阵列，假设阵列单元接收到的目标信号为E，成像时需要对阵列接收到的信号作如下处理：

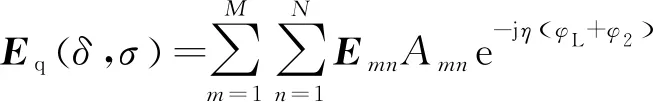
(14)

式(14)中，Emn为阵列单元接收到的场，Amn为阵列单元的幅度加权系数。参数η与成像系统的特性相关，η=1，可适用于被动式ISAR转台成像系统；η=2，可适用于主动式ISAR转台成像系统。

将式(1)、式(9)代入式(14)，化简整理后得：

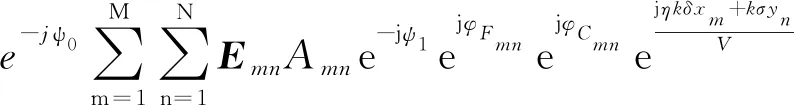
(15)

式(15)中，

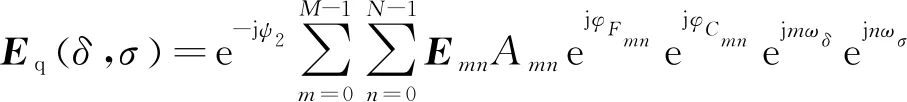
(16)

式(16)右边的系数满足|e-jψ2|=1，反映了像场的空间波动特性，对成像基本无影响，可忽略。求和运算则可用二维IFFT进行快速求解，则像场计算公式可简化为：

Eq(ωδ,ωσ)=IFFT(E·A·ejφFejφC)。

(17)

对比式(17)给出的转台成像快速算法与文献[17]算法可知，二者的差异在于转台成像公式中增加了一项相位补偿因子φC，该补偿因子与等效柱面半径ρ以及阵列单元偏离阵列中心的角度φ有关。

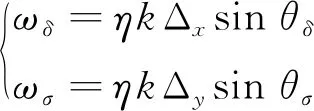
(18)

式(18)中，θδ、θσ为像点扫描角坐标，从而可得出像点角坐标计算公式为：

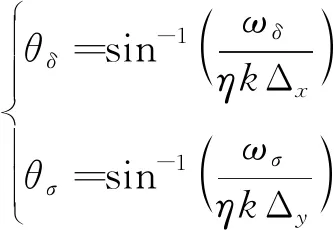
(19)

在转台成像系统中，目标往往位于合成虚拟柱面的轴线附近，此时需要用目标到局部柱面阵列中心的斜距R代替物距参数U。聚焦相位补偿因子φFmn的计算公式为：

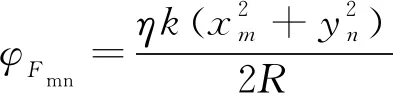
(20)

当转台系统的旋转角速度为ω时，令φ=ωt，t为时间，取位于合成的虚拟柱面中心的时刻为零。式(17)快速算法对应的相位加权系数可改写为：

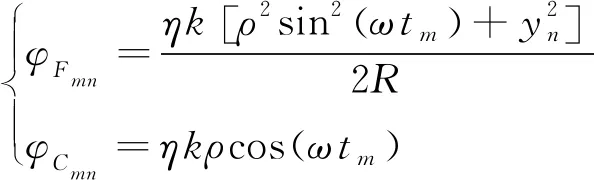
(21)

只要能够获得较为准确的目标距离参数R，采用式(21)进行配相，本文所述成像算法能够实现自动聚焦成像。相比传统ISAR成像算法，新算法更为简洁。

由式(17)、式(21)可知，本文给出的快速成像算法，采用了“幅相加权+IFFT”的技术体制，仅需进行一次IFFT快速运算即可获得目标的像，相比传统转台成像算法，大幅降低了运算量。

4 成像验证

采用电磁场仿真软件(如Feko、CST等)进行仿真，构造“R”形金属目标，其高0.4 m，宽约0.32 m。先进行被动成像仿真，用平面波对“R”形金属目标进行照射，计算转台成像所形成的虚拟圆柱阵面上的散射场分布，电磁仿真的示意图见图4(a)。系统工作频率为10 GHz，圆柱半径为1 m，柱面高度2 m，单元间距为半波长，“R”字形目标位于圆柱轴线上。通过电磁仿真获得的柱面上的场分布见图4(b)。

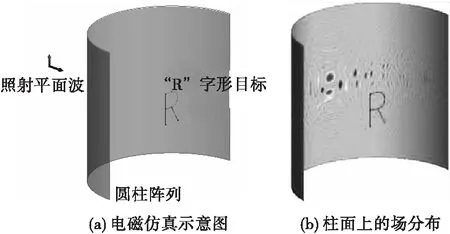
图4 被动成像电磁仿真及目标回波分布Fig.4 Passive imaging electromagnetic simulation and target echo distribution

对电磁仿真获得的柱面场分布数据进行处理，编写成像计算程序，取参数η=1，成像结果见图5，在所成的像中能够清晰分辨出“R”字形目标。

图5 被动式转台成像仿真结果Fig.5 Simulation results of passive turntable imaging

随后进行主动成像仿真，模拟竖直放置的一维线阵主动式转台成像，目标同样为“R”形金属目标。实际仿真时采用方位全向的偶极子天线探测目标，将该偶极子天线依次放置在转台成像所形成的虚拟圆柱阵面上的不同阵列单元的位置，计算天线馈电端口的s11参数，电磁仿真的示意图见图6(a)。系统工作频率为10 GHz，圆柱半径为1 m，柱面高度2 m，单元间距为四分之一波长，“R”字形目标位于圆柱轴线上。通过电磁仿真获得的目标散射场分布见图6(b)。

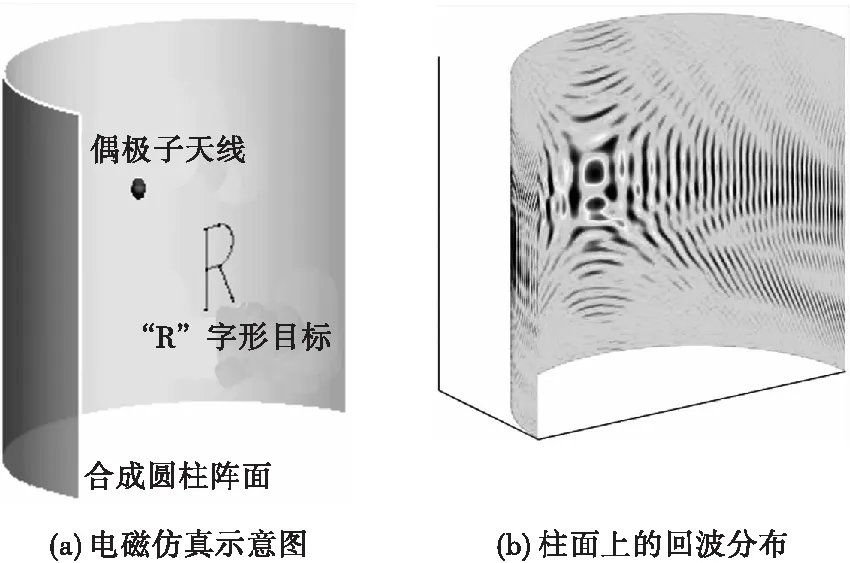
图6 主动成像电磁仿真及目标回波分布Fig.6 Active imaging electromagnetic simulation and target echo distribution

对电磁仿真获得的柱面场分布数据进行处理，编写成像计算程序，取参数η=2，成像结果见图7，在所成的像中能够清晰分辨出“R”字形目标。

图7 主动式转台成像仿真结果Fig.7 Simulation results of active turntable imaging

5 结论

本文提出一种不依赖于多普勒频移的ISAR成像新方法，该方法既适用于被动成像又可用于主动成像系统。此外，本文所述方法同样适用于圆柱扫描成像系统，也适用于柱面扫描合成孔径雷达成像。相比传统ISAR转台成像方法，该方法大幅降低了运算量，提高了成像速度，降低了硬件成本，具有重大的工程应用价值。