探究圆柱体表面积的变化问题,培养空间观念
中国农业大学附属小学 赵欣然 岳志刚
空间与人类的生存、生活密切相关,因此培养学生的空间观念是数学教学中的重要组成部分。空间的概念是抽象的,空间想象的建立分布在几何内容的学习中,而且空间观念的培养是一个长期的形成过程,所以在日常的几何教学中需要教师设计有意思、易操作、具体的实践活动,长期坚持、螺旋式上升培养学生的空间观念。在本文中,笔者通过设计切、拼、挖的操作活动,和学生一起探究圆柱体表面积的变化问题,同时提出使用动手操作、画图分析、观察想象的策略培养学生空间观念的观点。
一、在动手操作中,积累空间经验
动手操作是让思维外显的过程,能让抽象的数学知识直观化、具体化、简单化,打通感性与理性思维的通道。通过动手操作活动,可以调动手、眼、口、脑等多感官的协同参与,帮助学生积累空间经验,从而培养学生的空间观念。在探究圆柱体表面积变化问题的活动中,教师以生活中近似圆柱体的白萝卜为载体,设计了切、拼、挖的系列操作活动,和学生一起动手操作,展开探究,归纳规律,积累空间经验。
(一)切——“一刀生两面”
教师在课堂上设计了让每个学生都参与的切圆柱体形状萝卜的实践活动并要求做好记录。学生高兴地体验横切、纵切萝卜的各种情况,亲眼看到、亲手摸到不同的截面,在头脑中积累具体事物的形象,深度思考切圆柱体产生不同截面的原因,从而形成自己的空间观念。这样的体验活动是学生乐于主动参与的,这样直观的几何探究是儿童所能接受和内化的。具体经验归纳如下。
(1)横切:平行于上、下两个底面拦腰切。因为是平行于底面来切,所以会多出两个与底面相同的圆形截面,并且每切一刀都会增加两个完全一样的圆形截面,如图1所示。

图1 横切
(2)纵切:沿直径,垂直于底面纵切。因为是沿直径垂直来切,所以切完之后会多出两个长方形的截面,并且长方形的长是圆柱体的高,长方形的宽是圆柱体底面圆的直径,如图2所示。
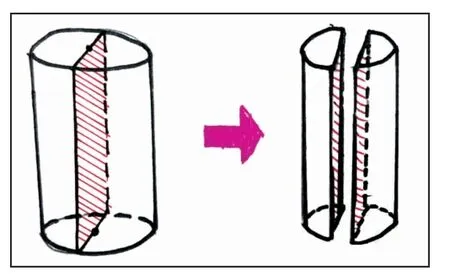
图2 纵切
另外,沿着底面圆的任意一条弦,垂直于底面纵切,都会增加两个一样大的长方形截面,并且长方形的长就是圆柱体的高,长方形的宽就是圆柱体底面圆的弦。只是,离底面圆心越远长方形截面就越小。
(二)拼——“一接消两面”
课前教师布置任务让学生寻找生活中的圆柱体,有茶叶筒、饼干筒、水杯、卷纸等。课堂上,学生尝试把两个完全相同或大小不同的多个圆柱体进行拼接。在拼接和打开的操作中,观察表面积的变化情况,积累活动经验,建立空间观念。具体经验归纳如下。
(1)两个完全一样的圆柱体拼在一起。因为拼接后有两个底面重合了,所以新图形的表面积会比原来两个圆柱体的表面积之和减少两个底面,如图3所示。

图3 两个相同圆柱体拼一起
(2)两个不同的圆柱体拼在一起。减少了两个小圆柱体的底面,一个是小圆柱体本身的下底面,另一个是覆盖在大圆柱体上的小圆柱体的底面,如图4所示。

图4 两个不同圆柱体拼一起
综上所述,通过动手切萝卜的活动,学生积累了“一切生两面”的空间经验,发现:①把圆柱体切一刀,可以横切,也可以纵切。其中,平行于底面的横切一刀,会增加两个和底面一样的圆形截面。沿底面圆的直径纵切一刀,会增加两个长方形的截面,其中长方形的长就是圆柱体的高、长方形的宽就是圆柱体底面圆的直径。另外,我们可以沿底面圆的弦纵切,离底面圆心越远长方形截面越小。②把圆柱体切开,无论是横切还是纵切,表面积都会增加。而且每切一刀,就会增加2个完全一样的面。每切n刀,就会增加2n个完全一样的面。通过动手拼接生活中圆柱体的活动,学生积累了“一接消两面”的空间经验,发现:把几个圆柱体底对底地拼起来,表面积会比原来表面积之和减少,并且每拼一次表面积就会减少2个完全一样的圆形底面。可以尝试把2个完全一样的圆柱体、3个完全一样的圆柱体……n个完全一样的圆柱体拼接到一起,会减少(n-1)×2个圆形底面。
二、在画图分析中,提升空间想象能力
画图分析的方法可以帮助学生描述动手操作的过程和结果,直观地帮助学生突破空间想象的难点,找到现象背后的本质,是培养学生空间观念的有效手段。
在探究圆柱体表面积变化问题中,画图分析的策略贯穿整节课的学习,起到了很重要的作用。在动手操作活动的基础上,学生能结合活动经验和认知情况在头脑里形成表象,并能直观地画出透视图,把复杂的数学问题变得简明、形象,帮助学生直观地理解数学问题,提升空间想象能力,发展空间观念。
课堂上,教师有意识地指导学生使用画图分析的方法,借助直观图、透视图来理解抽象的数学知识。特别地,在解决斜切之后截面是什么形状的问题中,画图分析能帮助学生找到了现象背后的原因,纠正了开始错误的判断,提升了空间想象能力。画图发现,斜着切其实有三种典型的切法,包括从侧面切到另一端的侧面、从底面切到侧面、从上底面切到下底面,具体归纳如下。
(1)侧面→侧面的斜切:从圆柱体侧面上的一点切到另一侧的某个点,截面是椭圆形。因为圆柱体的侧面是一个曲面,开始切时,只触碰到圆柱体侧面的一点,后因离中心轴越来越近,切到的面积会越来越大,后又因离开中心轴,面积开始变小,直到从另一点离开圆柱体,所以形成的截面是椭圆形的,如图5所示。

图5 侧面→侧面的斜切
(2)底面→侧面的斜切:从圆柱体底面起刀,切向侧面收刀,截面是马蹄形。因为起刀位置在平面,收刀位置在曲面,所以切出来的截面头部是平的,后来是有弧度的曲面图形,整体来看是像马蹄一样的形状,也可以理解成是椭圆的一部分,如图6所示。
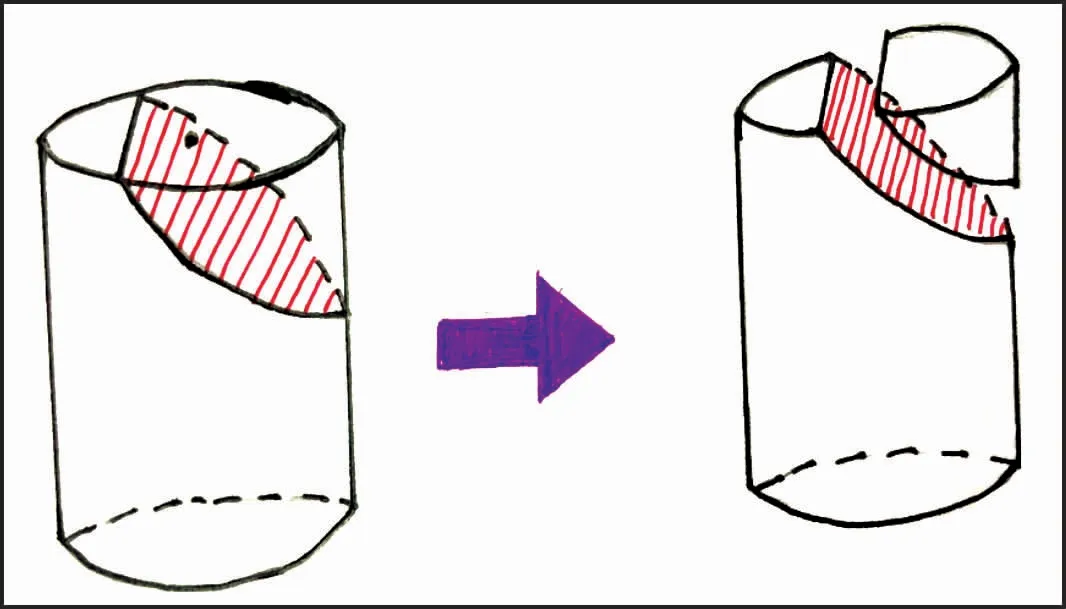
图6 底面→侧面的斜切
(3)底面→底面的斜切:从圆柱体上底中心点偏左或偏右的地方选取一条弦,切到下底中心点偏右或偏左的那条弦,截面是鼓形。因为起刀位置是平面,而且选取的弦比底面圆的直径短,切的过程中会经过一条直径,收刀的位置是底面圆另一端的弦,所以截面是鼓形,也是椭圆的一部分,如图7所示。

图7 底面→底面的斜切
在解决斜切之后圆柱体表面积的变化问题时,学生比较容易想象出侧面→侧面的斜切截面是椭圆形,也能判断出底面→侧面的斜切截面是马蹄形。但是多数学生错误地认为上底面→下底面的斜切截面是长方形,可能是把纵切和此类斜切搞混淆了。但是通过画图分析切的过程(见图7),我们可以清晰地看到起刀弦的长度和收刀弦的长度都比经过的直径短,所以判断截面肯定不是长方形而是鼓形。另外,在描述斜切中马蹄形和鼓形的画图中,我们可以判断出这样的截面都是椭圆形状的一部分。在这两处分析中,学生很难直接准确判断或想象,但是通过画出斜切之后的透视图,学生就能清晰地分析出斜切之后的变化情况,其中画图分析的策略能有效帮助学生提升空间想象能力,发展空间观念。
三、在观察想象中,挖掘创新意识
想象就是把研究对象在头脑中进行操作,通过分析位置、度量等关系产生相应的思考。通过观察立体图形,想象着对其进行一些操作,判断出操作结果的情况,是培养学生空间观念的高阶目标。观察想象,是更加抽象的思维,能帮助学生从动手操作实物向动脑操作表象过渡。在日常教学中,教师有意识地鼓励学生常观察会想象,有助于实现空间观念的建立。在本节课的教学中,教师多次使用观察想象的策略,挖掘学生的创新意识。具体举例如下。
(一)斜切——“切完拓下来”
学生比较容易想象出横切和纵切的截面情况,但很难想象出斜切之后会呈现出什么样的截面。于是,大家想到最直接的解决办法就是切一刀,切完就能看出截面的具体形态。边切边想象,学生归纳出三种典型的斜切截面,并提议把斜切截面拓下来(见图8),这样看到的更清晰。学生边观察想象,边尝试操作,在体验中有创新,把空间观念发展到高点。

图8 斜切——“切完拓下来”
(二)挖——“挖完仔细算”
从圆柱体上底挖穿至下底,挖走一个圆柱体,原来圆柱体的表面积又会发生哪些变化呢?在解决问题的过程中,我们发现动手挖穿取下一个圆柱体是很难的操作,于是就需要观察想象的策略发挥作用。学生在头脑中建立一个大圆柱体的概念,然后在头脑中对圆柱体进行挖穿的操作(见图9),可以想象出原来圆柱体的表面积减少了两个小圆柱体的底面积,又增加了新露出的小圆柱体的侧面积。新图形的表面积和原来圆柱体的表面积相比,表面积是增加了还是减少了,需要结合具体形状和数据来仔细推算。
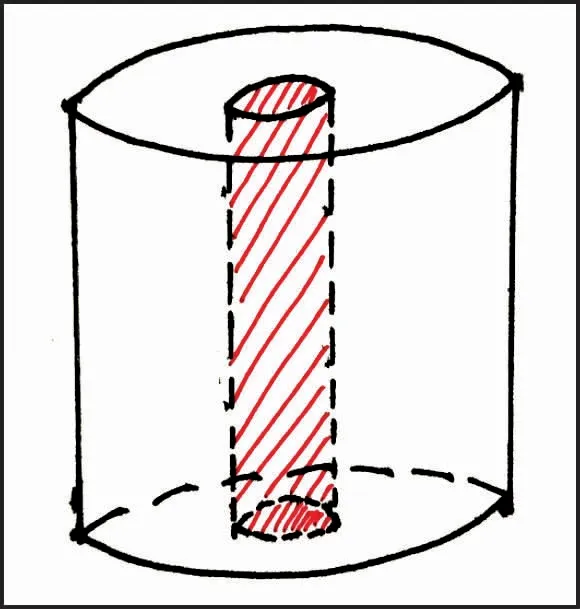
图9 挖——“挖完仔细算”
综上所述,通过探究圆柱体表面积的变化问题,我们发现动手操作、画图分析、观察想象是学生积累基本活动经验、发展空间观念的有效方式。三者之间相辅相成,其中动手操作是培养空间观念最直接的方式。画图分析可以帮助学生描述动手操作的过程和结果。观察想象是把动手操作实物引向动脑操作表象的过程。教师在图形与几何领域的教学中,恰当使用如上策略,可以帮助学生建立空间观念,发展数学思维。

