基于ARIMA时间序列的瓦斯浓度预测研究

林旭杰，孟祥瑞

(安徽理工大学 1.计算机科学与工程学院；2.经济与管理学院，安徽 淮南 232001)

随着对煤矿开采的增大，瓦斯爆炸已经成为煤矿生产中的严重问题，根据国家应急管理部发布的消息表明，瓦斯爆炸是煤矿安全生产中存在的最大的安全隐患事故[1]。瓦斯爆炸存在一定的范围，当空气中的瓦斯浓度在百分之五到百分之十六的时候，出现明火就会发生爆炸，爆炸会产生冲击波和有毒气体。因此在煤矿生产中对于瓦斯浓度的精准预测显得格外重要。近些年来，随着人工智能算法的逐步应用，作为人工智能领域的数据挖掘算法成为了发展重心[2]，许多研究人员将数据挖掘算法应用在一些工程问题上来解决问题。针对煤矿瓦斯浓度预测精度问题，研究人员通过实验和模拟方法对煤矿掘进工作面瓦斯爆炸做出大量的研究。贾澎涛[3]等利用煤矿瓦斯数据的空间特性提出一种基于卷积神经网络与单元神经网络的煤矿瓦斯浓度预测模型，实验结果表明，该模型与传统模型相比，误差明显降低，在煤矿瓦斯浓度预测领域中具有一定的指导意义。王雨虹[4]等提出一种优化算法来优化长短记忆神经网络的瓦斯浓度预测模型，对瓦斯浓度时间序列进行分析和去噪，再通过重构线性缩减因子c，利用高斯变异方法改进优化算法，以此建立瓦斯浓度预测模型。与传统模型相比，实验结果表明，该模型误差比传统模型误差有显著性降低，提高了瓦斯浓度预测模型的预测性能。付华[5]等提出一种深度长短记忆神经网络的传感器瓦斯浓度预测模型，利用相关系数法选出变量作为模型参数，再通过优化算法对该参数进行优化，最终建立动态预测模型，实验结果表明，该模型的预测性能较好，在煤矿瓦斯浓度预测领域具有一定的参考价值。张新建[6]等提出一种长短期记忆神经网络与小波阈值降噪结合的瓦斯浓度预测模型，对原始数据进行降噪处理，再利用长短期记忆网络对其进行预测，并且与传统模型进行比较，研究结果表明，该模型的预测精确度有明显提高。徐琦[7]等提出传播网络、径向基函数神经网络和回归神经网络对瓦斯浓度进行预测，实验结果表明径向基函数神经网络的预测效果更好。

综上所述，针对目前瓦斯浓度预测问题，以往研究存在预测准确性不高和数据量少等问题，因此本文在以往研究的基础上，充分利用时间序列的特点，建立基于时间序列的差分自回归平均模型(Autoregressive Integrated Moving Average Model, ARIMA)，对煤矿瓦斯浓度进行预测。实验结果表明，ARIMA模型预测的平均绝对误差比SVR模型的平均绝对误差降低了13.27%。

1 建模原理

ARIMA模型是博克斯(Box)与詹金斯(Jenkins)在20世纪70年代提出来的一种时间序列算法，也被命名为Box-Jenkins模型[8]。ARIMA作为一种时间序列算法，其主要包括时间序列平稳性检验、模型定阶、模型检验以及模型预测四个步骤。具体过程如下。

1.1 平稳性检验

由于ARIMA模型不能捕获非稳定时间序列的变化规律，因此，首先需要对时间序列进行平稳性检验[9]。时间序列的平稳性检验一般有两种方法：第一种方法是直接通过绘制出来的时间序列数据的滚动标准差来判断，观察时序数据的变化趋势来判断是否平稳；第二种方法为单位根检验法(ADF)，利用求出来的ADF值来判断时间序列数据在置信区间上是否显著，若具有显著性，则可以确定该时间序列数据是稳定的，如果不具有显著性，那么可知该时间序列不稳定[10]，公式(1)为时间序列的均值表达式。

Xi=φ1Xt-1+φ2Xt-2+…+φpXt-p+εt

(1)

式(1)中Xi(i=t,t-1,…,t-p)表示非平稳时间序列；φ1,φ2,…,φp为带估算的自回归参数；εt为白噪声过程。

若得出的时间序列数据为非平稳序列，则需要利用差分法将其处理为平稳序列。差分法主要分为一阶差分法和广义差分法，一阶差分法指的是函数中连续相邻两个数值的差。当自变量由t-1到t时，函数X=Xt的改变量ΔXt=Xt-Xt-1(t=1,2,…)，称为函数X(t)在点t的一阶差分。

若得到的差分结果仍为非平稳序列，则可以在一阶差分的基础上继续差分，d次差分表达式如式(2)所示。

▽dXt=(1-B)dXt=Yt=Wt

(2)

式(2)中Wt是d阶差分后发的平稳序列；B为延迟算子，表示时间序列的时间指标。

一般情况下，瓦斯浓度时间序列经过一次差分即可转换为平稳性序列,不需要进行多次差分[11]。

1.2 模型定阶

ARIMA模型的p值与q值通常用自相关函数(ACF)与偏自相关函数(PACF)获取。观察绘制出来的ACF与PACF图，其中曲线第一次穿过上置信区间的横坐标值即为p、q的值。公式(3)为自相关函数表达式。

(3)

式(3)表示间隔为k的时间序列之间的相关系数值，其中k是间隔的阶数。公式(4)为偏自相关函数表达式。

(4)

式(4)中φkk=φk-1，φkkφk-j；ρk指的是时间序列的自相关函数。

1.3 模型检验

通过上述步骤后，应当对时间序列模型展开评价，以验证所选用的模型是否合理。针对模型合理性检验，一般从两方面判断：一方面需要验证时间序列模型的参数值是否具有显著性；另一方面是验证时间序列模型的残差序列是否为白噪声序列，残差序列通过时间序列模型得到，若残差序列的自相关函数不显著为零，则可以确定为独立的。通过这两方面可以得到，若验证通过，则可以确定该模型合理，若验证不通过，应当重选模型，再按照上述步骤，最终选出有效的模型[13]。

1.4 模型预测

在对数据进行采集后，利用时间序列算法对其进行平稳化处理，通过识别确定阶数与模型检测，最终建立时间序列模型。在后续实验中对模型进行预测以此来判断模型的平均绝对误差(MAE)[14]。本文对于建立ARIMA模型的设计流程如图1所示。

图1 ARIMA模型预测流程图

2 实验分析

本文数据采用已发生瓦斯爆炸事故的贵州某煤矿监测瓦斯浓度工作面数据，该煤矿属于高瓦斯矿井，将监测到的数据上传到管理系统，并存储到硬盘当中，选用2020年8月1日0点至8月9日23:59点共59418条瓦斯浓度数据作为本文实验内容的样本。由于瓦斯浓度数据的获取并没有规律，因此从工作面传感器得到的数据发现每秒时间约有四条数据，所选取的数据量庞大。对数据集按照7：3的比例分开，将前面70%的监测数据用于模型训练拟合，后面30%的数据作为该实验的瓦斯浓度预测验证。

2.1 平稳性验证

利用Python语言绘制出折线图，通过标准差来确判断该原始数据时间序列图是否稳定。如图2所示为贵州某煤矿掘进工作面在2020年8月1日0点到2020年8月9日23:59的原始数据图。根据图示能够看出瓦斯浓度标准差随着时间的变化缓慢上升，每个时间点的标准差也有所差别，可以判断该图为不稳定序列。

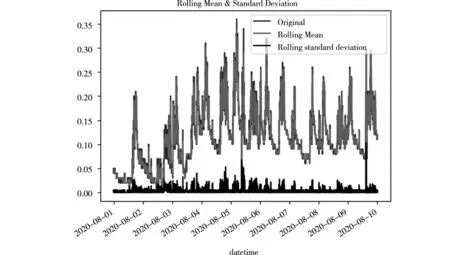
图2 煤矿瓦斯浓度时间序列图

对于非平稳数据利用差分法转换为平稳序列，然后利用单位根检测法检验是否平稳，如图3所示为一阶差分后的效果图，表1为利用单位根检测法检测的数据表。根据表1可以得知，1%的临界值大于测试统计值，则99%的置信度下为稳定序列，因此可表明该时间序列满足ARIMA的要求，并得到d的值为1。

表1 ADF测试数据

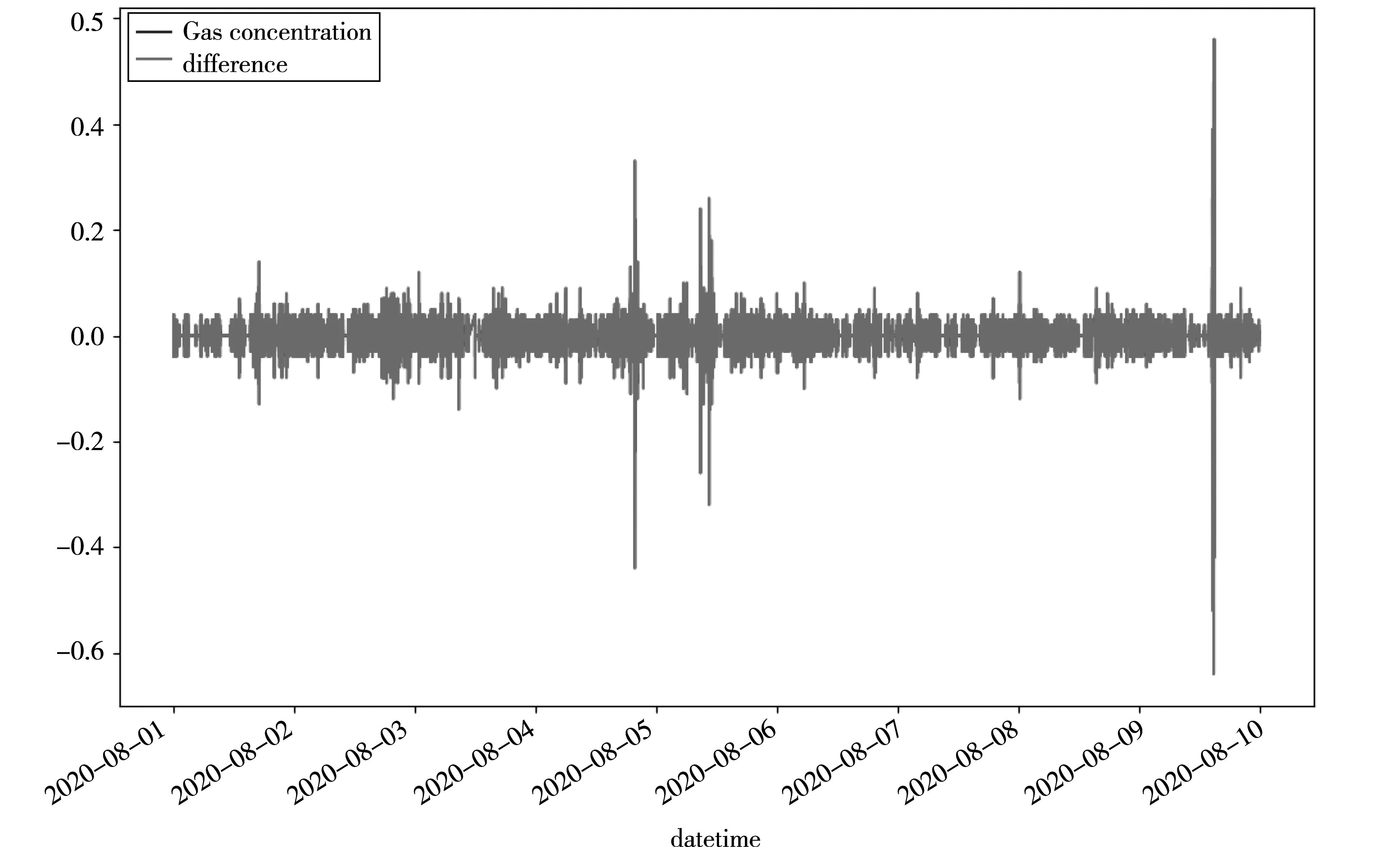
图3 一阶差分后效果图

2.2 确定阶数

对时间序列利用一阶差分法处理成为平稳序列，然后利用自相关函数ACF和偏自相关函数PACF对参数p、q进行确定。图4为经过一阶差分后的ACF和PACF图，通过观察发现ACF在一阶差分达到顶峰值之后呈现拖尾衰退现象，PACF图在一阶差分达到顶峰值后呈现拖尾衰退现象。并由图4可得，ACF和PACF系数第一次经过置信度上下限的值均为1，因此p与q的值均为1。

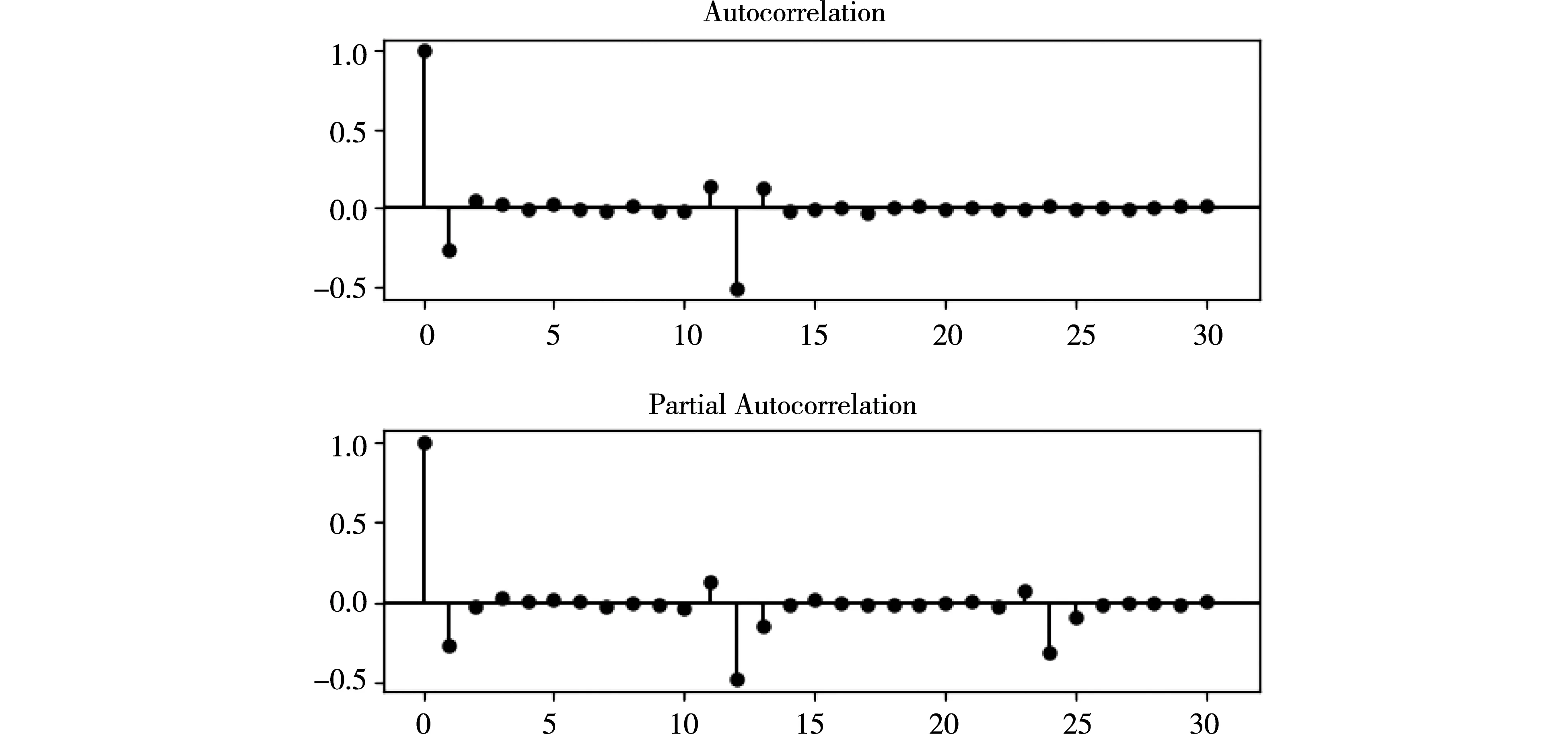
图4 ACF和PACF图

2.3 模型检验

通过对模型的差分和定阶，确定了p、d、q的值，确定瓦斯浓度预测模型为ARIMA(1,1,1)。在对模型预测之前需对模型进行检验，即对模型拟合进行评价，若拟合效果较差，则需要重写进行差分、定阶处理[15]。图5为ARIMA模型拟合图，横坐标为煤矿掘进工作面所选取的数据条，纵坐标为瓦斯浓度值；通过时间预测模型进行分析，得到该拟合模型的MAE为0.03。如图6所示，残差ACF与残差PACF都在置信区间内，因此可得，过去的数值与现在的数值几乎没有相关，即该模型符合要求。

图5 拟合效果图

图6 残差ACF与残差PACF

2.4 模型预测

图7所示为本文通过ARIMA时间序列算法对数据集后30%的测试集的瓦斯浓度数据进行预测得到的预测图。得到该算法模型的MAE为0.0196。为了验证ARIMA算法在瓦斯浓度预测中的鲁棒性，本文选取的对比模型为SVR模型，如图8所示为SVR模型的预测值与真实值的结果实验图。通过选择MAE作为两者模型性能评价标准，其中通过实验结果可知，SVR模型预测的MAE值为0.0226，ARIMA模型预测的MAE值为0.0196，ARIMA模型预测的MAE相比SVR模型预测的MAE值降低了13.27%。

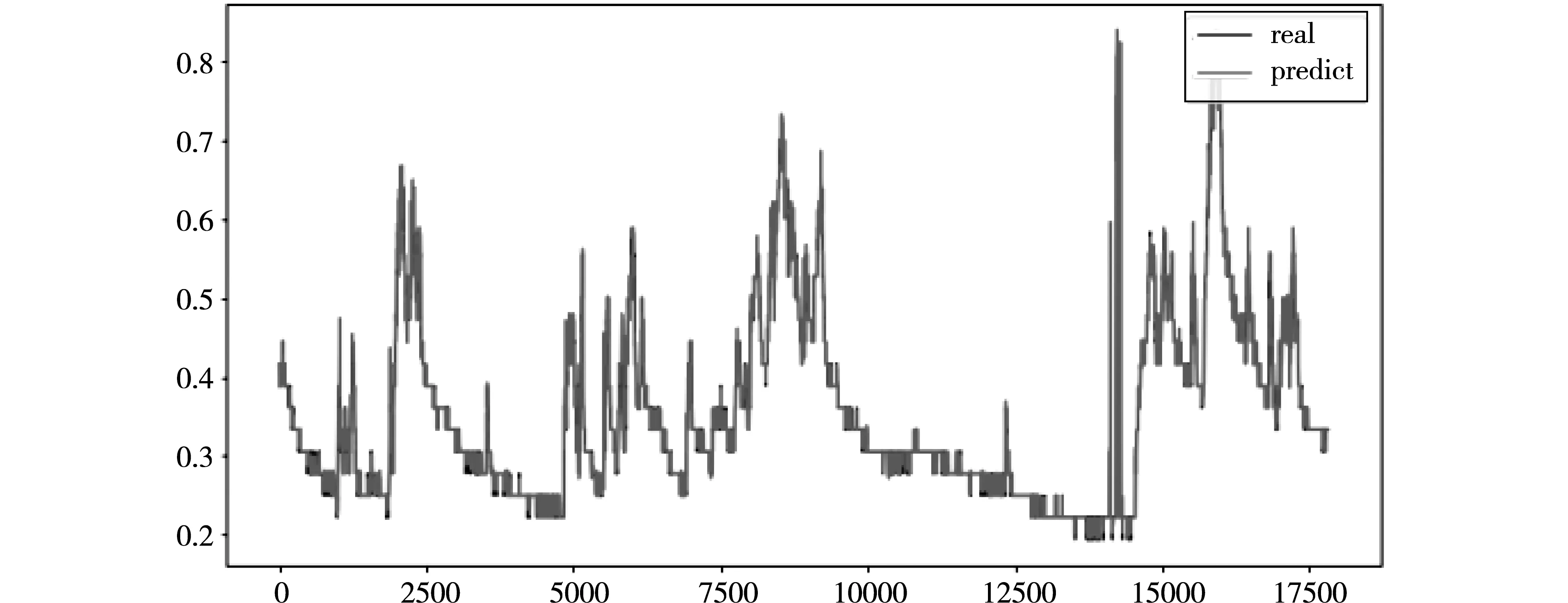
图7 ARIMA模型预测

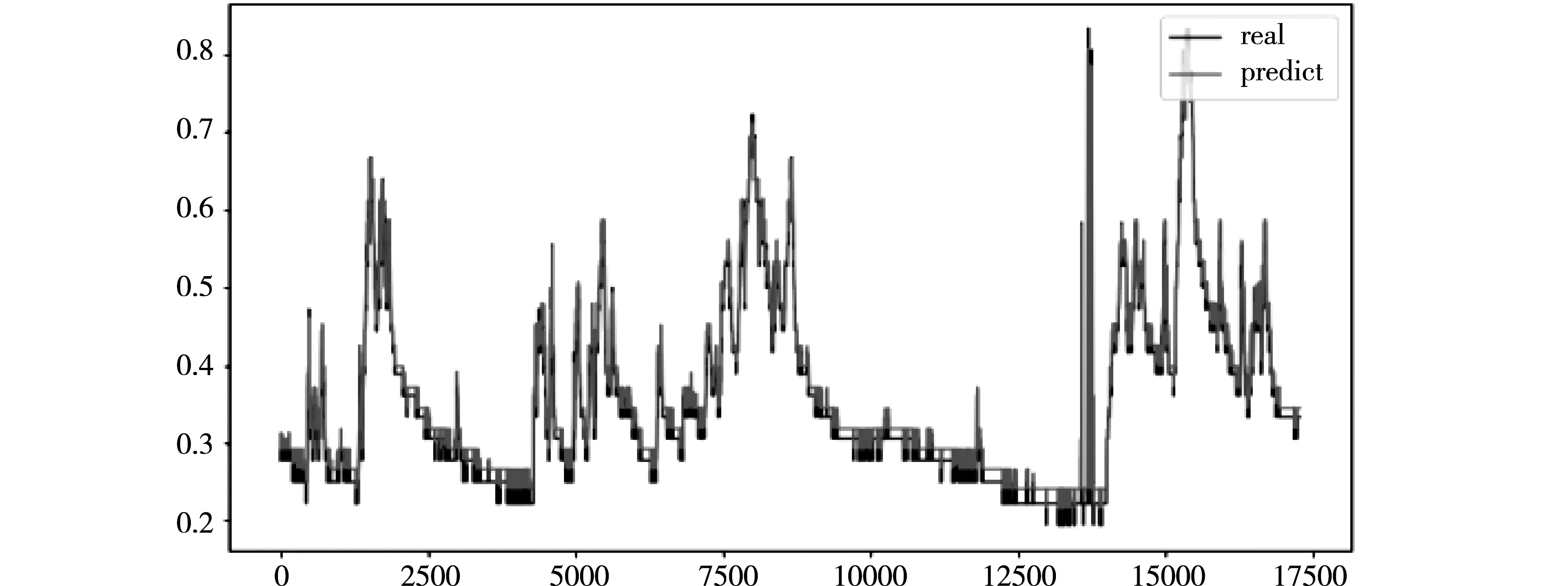
图8 SVR模型预测

3 结论

结合当今煤矿瓦斯安全预测工作，针对瓦斯浓度预测精度问题，本文提出在ARIMA时间序列模型下的瓦斯浓度预测研究，通过对煤矿工作面的瓦斯传感器数据为研究对象进行实证分析，与传统的SVR模型进行预测对比可得，本文的MAE值明显低于SVR模型的MAE值，有效地提高瓦斯浓度的预测精度。由于煤矿行业的特殊性，煤矿工作面的信息难以获取，对于一些其它信息的评价会受到影响，因此在后续的实验研究中，应当获取到更充足的数据，不断提高瓦斯浓度预测的精准度与煤矿的安全性。