砼芯水泥土桩复合地基工作性状研究
俞建霖,杨晓萌,周佳锦,徐山岱,龚晓南,赵新文
(1. 浙江大学滨海和城市岩土工程研究中心,浙江 杭州,310058;2. 浙江省城市地下空间开发工程技术研究中心,浙江 杭州,310058;3. 浙江加州国际纳米技术研究院台州分院,浙江 台州,318000;4.苏州中车建设工程有限公司,江苏 苏州,215218)
随着中国经济的高速发展,城市对工程建设的需求也进一步扩大。为应对在实际工程中可能遇到的软土等不良地质条件带来的挑战,越来越多的新兴技术被应用到地基处理中。砼芯水泥土桩(以下统称为CDCM桩)是在传统的水泥土搅拌桩施工完毕后插入预制混凝土芯形成的一种复合桩型,结合了混凝土桩强度高和水泥土桩侧摩阻力大的优点,可以有效提高地基承载力,减小沉降,且具有较好的经济性。
学者们通过室内试验、数值模拟和解析计算的方法对CDCM 单桩工作机理进行了研究。吴迈等[1]通过静载荷试验研究了CDCM桩的单桩承载力及其影响因素。周佳锦等[2]通过室内模型试验,研究了砼芯和水泥土桩竖向应力沿桩长的分布形式、桩侧及桩端阻力与相对位移的关系,发现砼芯底部水泥土桩竖向应力存在“突增效应”。董平等[3]采用弹塑性有限元方法研究了CDCM 桩在竖向荷载下的力学性状,包括桩土应力比、砼芯竖向应力以及内外芯界面侧摩阻力沿桩长的分布形式。顾士坦等[4]基于复合材料力学原理及明德林位移解,采用理论分析的方法,推导出CDCM 桩竖向应力、界面侧摩阻力的表达式。王安辉等[5]通过建立黏土中CDCM桩的水平荷载-位移曲线,研究水平荷载下CDCM桩的工作机理并对各影响因素进行分析。
近年来,CDCM 桩作为一种新型地基处理手段,已被应用于高速公路、铁路等实际工程中,因此,CDCM 桩复合地基的工作性状逐渐受到国内外学者的关注。王驰等[6]通过弹塑性有限元数值模拟研究了CDCM 桩复合地基的荷载传递规律及其影响因素,并提出CDCM 桩的优化设计方法。BERGADO等[7]通过现场试验和有限元分析,研究了路堤荷载下CDCM桩的工作性状及其影响因素,发现含芯率对竖向承载力有较大影响,而水平承载力对芯长比的变化更加敏感。YE 等[8]采用有限元法,建立了路堤下CDCM 桩复合地基的三维模型,分析了砼芯与水泥土桩长、含芯率、桩间距以及路堤高度对复合地基荷载传递的影响并提出了EBGEO[9]的修正方法。钟佳男[10]通过建立刚性基础下CDCM桩复合地基的轴对称数值分析模型,研究其工作机理以及荷载水平、芯长比、含芯率、复合地基置换率等因素的影响,并将其与柔性基础下CDCM 桩复合地基的工作特性进行比较,分析二者在荷载传递规律与变形机理上的差异。
目前人们对CDCM 桩复合地基的研究多集中于现场实验和数值模拟,解析分析与设计理论研究相对较少。叶观宝等[11]在不考虑砼芯变形条件下,推导出刚性基础下CDCM 桩复合地基桩土应力比的计算公式。ALAMGIR等[12]通过将桩土划分为若干个单元体以考虑地基土分层并采用迭代递推的方法推导出路堤荷载下柔性桩复合地基的沉降计算公式,但是未考虑桩土相对位移以及下卧层沉降。俞建霖等[13]通过对砼芯-水泥土桩-桩周土的界面作用机理进行假设并考虑相对位移对侧摩阻力的影响,提出了一种刚性基础下CDCM 桩复合地基沉降的计算方法,但该方法未考虑地基土分层且计算仅适用于砼芯等长的情况。
本文作者基于文献[13],考虑地基土分层以及实际工程中砼芯与水泥土桩长可能不相等的情况,提出刚性基础下砼芯水泥土桩复合地基工作性状的迭代分析法,并通过与原位实测的荷载-沉降曲线进行对比,验证该计算方法的合理性。对CDCM 桩复合地基的工作性状进行研究,探讨含芯率、芯长比、面积置换率以及荷载水平等因素对复合地基桩土应力比与沉降的影响。
1 解析分析法
1.1 研究对象
将单桩及其影响范围内的土体作为研究对象,基于“典型单元体”的概念简化计算模型,如图1所示。一个CDCM 桩复合地基的典型单元体包括砼芯(实心)、水泥土桩以及桩周土,其中CDCM桩长为L,半径为rm;砼芯长度为Lc,半径为rc;纯水泥土桩段(不含砼芯)长度为L-Lc;分布在砼芯、水泥土桩和桩周土上的荷载分别为σc0,σm0和σs0;桩间距为sc;单桩影响范围为de,且de与sc存在如下关系[14]:
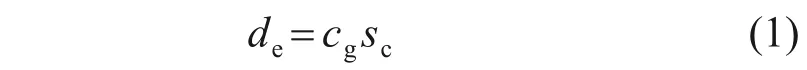
式中:cg为与布桩形式有关的常数,一般取1.05,1.13和1.29,分别对应于三角形、正方形和楔形布桩形式。
由于桩周土、水泥土桩和砼芯的弹性模量处于不同数量级,在竖向荷载的作用下,刚性基础下砼芯-水泥土桩-桩周土发生相对位移,界面上产生正侧摩阻力,从而引起三者间的荷载传递[13]。在桩端平面处,水泥土桩刺入下卧层;而在砼芯底部,有砼芯刺入水泥土桩。
1.2 基本假设
对于砼芯、水泥土桩及桩周土,本文进行如下假设:
1)砼芯、水泥土桩及桩周土均为均质各向同性线弹性体,刚性基础板刚度无穷大。
2)砼芯、水泥土桩及桩周土均只发生竖向变形,径向变形可忽略不计。
3)桩周土-水泥土桩-砼芯三者间的侧摩阻力与桩端阻力均符合理想弹塑性模型假设的荷载传递模式。
1.3 迭代分析模型建立
取桩顶平面与CDCM 桩中心线的交点为原点O,过原点在桩顶平面内任取一条射线为极轴r,以深度方向为z轴正方向,建立如图1(b)所示的三维柱坐标系。将复合地基在桩长L范围内等分为n段,各微元段高度为ΔL,分别选取砼芯、水泥土桩、桩周土微元段进行受力分析。图1(b)中,nc为Lc范围内的微元段数。
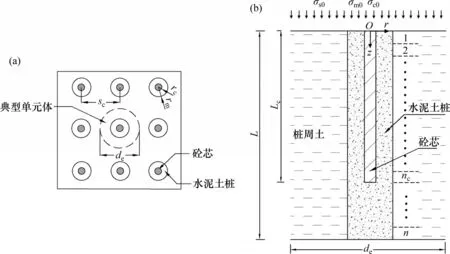
图1 砼芯水泥土桩复合地基示意图Fig.1 Schematic diagram of concrete-cored DCM pile
1.3.1 复合桩段
复合桩段砼芯、水泥土桩、桩周土第i个微元段的受力如图2 所示(根据典型单元体荷载与几何的对称性,单元体外(桩周土)边界上的剪应力等于0)。图2中,σs(i-1),σm(i-1)和σc(i-1)分别为作用于桩周土、水泥土桩和砼芯第i个微元段顶部的竖向应力。
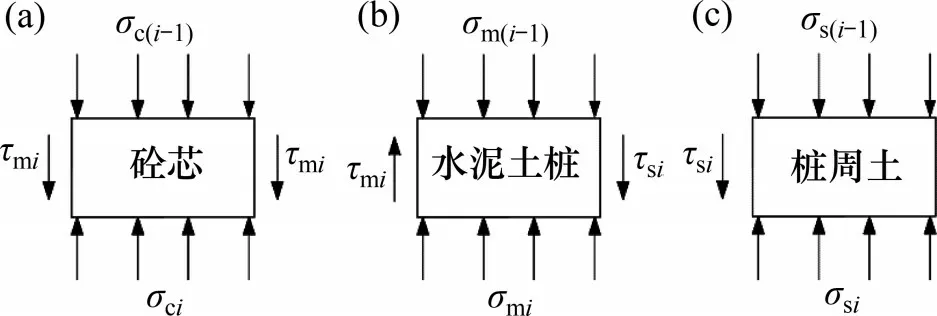
图2 复合桩段微元段受力示意图Fig.2 Stress diagram of each element in composite pile section
根据受力平衡,有:
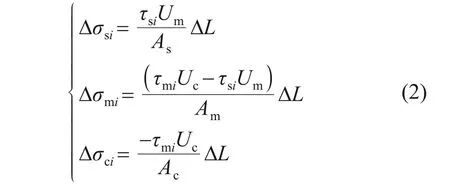
式中:Δσsi,Δσmi和Δσci分别为桩周土、水泥土桩与砼芯第i个微元段底部与顶部的竖向应力差;As,Am和Ac分别为单桩影响范围内桩周土、水泥土桩和砼芯的截面积;Um和Uc分别为水泥土桩与砼芯截面周长;τmi和τsi分别为第i个微元段砼芯-水泥土桩、桩-土界面侧摩阻力。
令C1=(UmΔL)/As,C2=(UcΔL)/Am,C3=(UmΔL)/Am,C4=(UcΔL)/Ac,则上述平衡方程可简化为
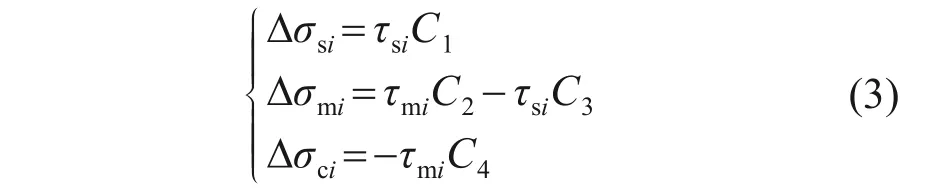
根据假设并结合胡克定律可得复合桩段桩周土、水泥土桩和砼芯第i个微元段的压缩量Ssi,Smi和Sci为:
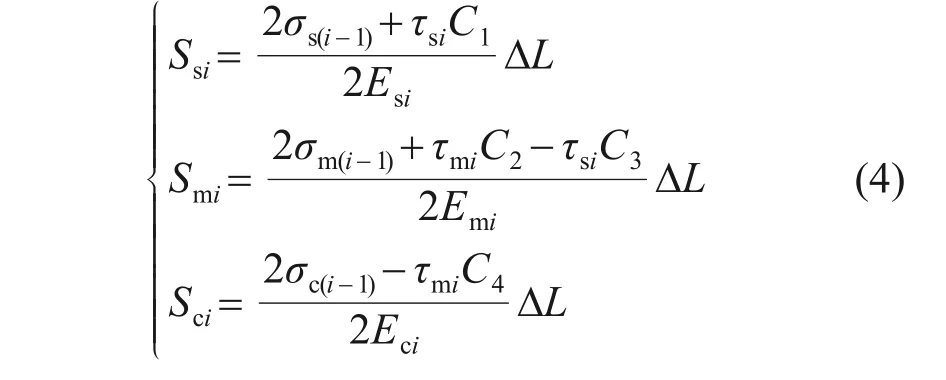
1.3.2 纯水泥土桩段
纯水泥土桩段桩、土第i微元段的受力如图3所示。根据受力平衡,有:
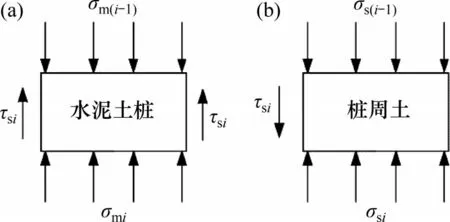
图3 纯水泥土桩段微元段受力示意图Fig.3 Stress diagram of each element in pure cement pile section
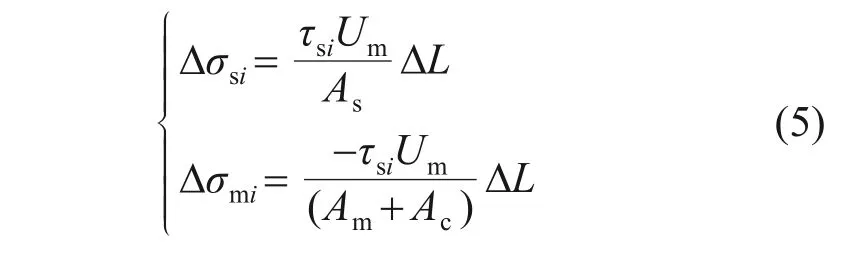
令C5=(UmΔL)/(Am+Ac),则有:

纯水泥土桩段水泥土桩第i个微元的压缩量为
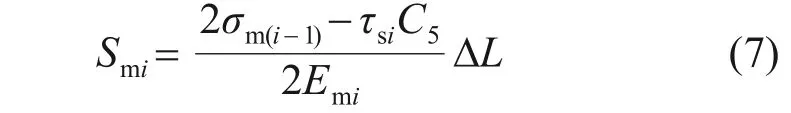
由式(3)可计算得到桩周土应力变化量Δσsi,由式(4)可计算得到压缩量Ssi。
1.3.3 侧摩阻力函数模型
基于理想弹塑性荷载传递模型的假设,桩-土(外)界面侧摩阻力表达式[15]为
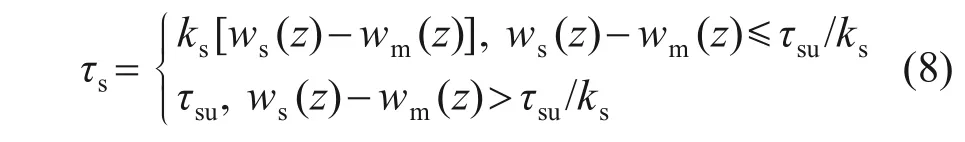
式中:z为埋深;ks为深度z处桩-土界面摩擦因数;ws(z)和wm(z)分别为深度z处桩周土与水泥土桩的竖向位移;τsu为外界面深度z处极限侧摩阻力。
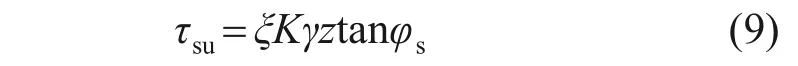
式中:ξ为钻孔灌注桩与劲性搅拌桩桩侧摩阻力换算关系的修正系数,取值为1.41~1.62[16],本文取ξ=1.4。K,φs和γ分别为深度z处桩周土的静止土压力系数、内摩擦角以及天然重度(地下水以下取有效重度)。
砼芯-水泥土桩(内)界面侧摩阻力表达式为
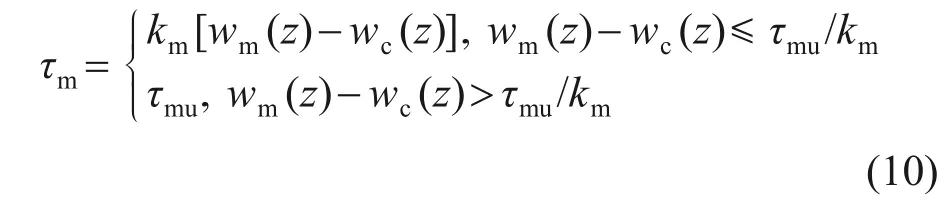
式中:km为砼芯-水泥土桩(内)界面摩擦因数;wc(z)和wm(z)分别为深度z处砼芯与水泥土桩的竖向位移;τmu为内界面深度z处极限侧摩阻力
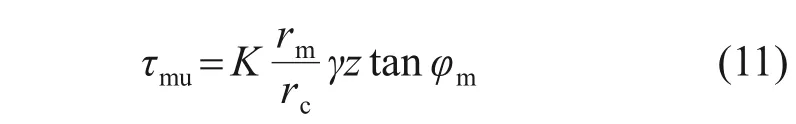
式中:rm/rc可用于表征土压力从外界面向内界面的等效传递;φm为内界面摩擦因数,可以根据文献[17]中的试验数据进行取值。
1.4 复合桩段迭代计算过程
复合桩段迭代计算过程如下:
1) 首先将复合地基在CDCM 桩长L范围内纵向等分为n段,每个微元段的长度ΔL=L/n,则砼芯长度Lc范围内包含的微元段数nc=Lc/ΔL。对于非均质土,应在土层分界面处设置分界线并根据相应土体参数进行赋值以实现土体分层。
2) 已知上部总荷载为F,假设在桩顶处桩周土、水泥土桩和砼芯的初始竖向应力分别为σs0,σm0和σc0(如图1(b)所示)且三者关系满足如下关系式:
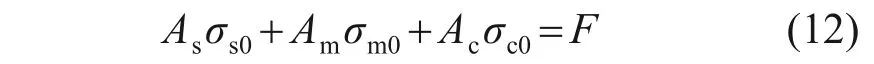
3) 复合桩段应力与位移计算过程如下(以第i段为例,其中i=1,2,3,4…,nc)。
a.首先基于内、外界面侧摩阻力形式的假设(式(8)~(11)),将其分别代入式(4)中得到桩周土、水泥土桩与砼芯第i个微元段的压缩量Ssi,Smi和Sci在不同条件下的表达式。
若内、外界面均未达到侧摩阻力极限状态,则Ssi,Smi和Sci的表达为
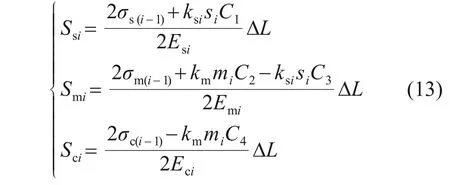
式中:si为第i个微元段桩、土的相对位移;mi为砼芯、水泥土桩的相对位移,由于刚性基础下砼芯、水泥土桩、桩周土顶部的竖向位移相等,所以相对位移si和mi可通过式(14)和(15)求得:
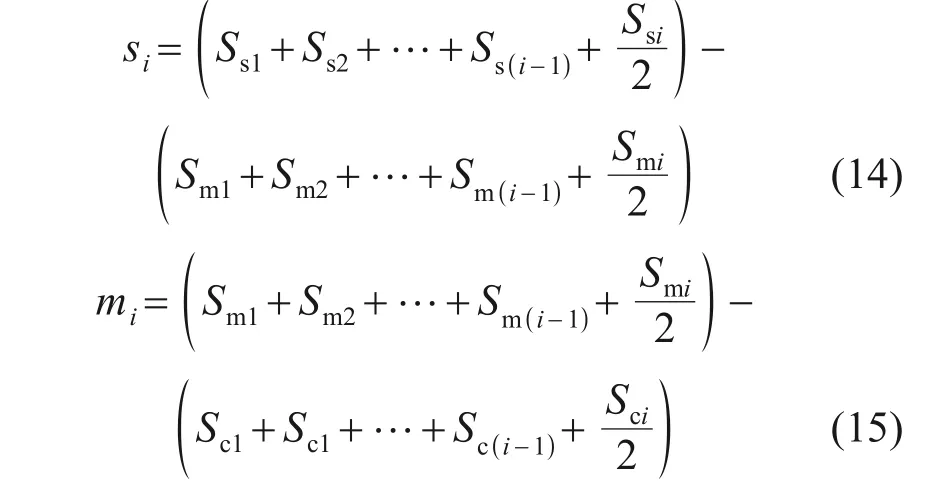
若内界面达到极限状态而外界面未达到极限状态,则Ssi,Smi和Sci的表达式为
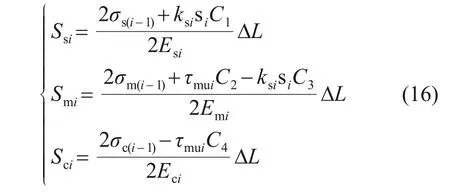
式中:τmui为第i个微元段内界面极限侧摩阻力。结合式(11),有:
式中:γi和Ki分别为第i个微元段桩周土的天然容重与静止土压力系数。
若外界面达到极限侧摩阻力而内界面未达到极限状态,则Ssi,Smi和Sci的表达式为
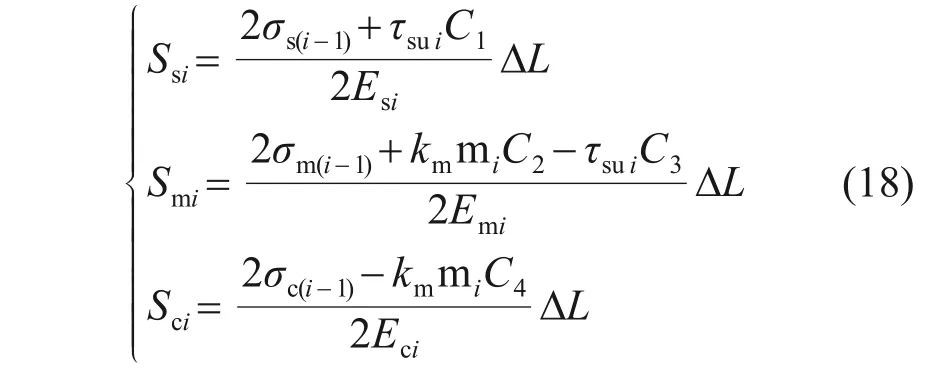
式中:τsui为第i个微元段外界面极限侧摩阻力。结合式(9),有:
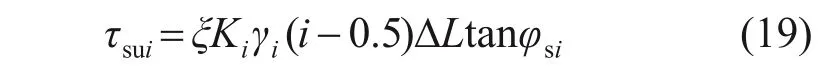
式中:φsi为第i个微元段桩周土的内摩擦角。
若内、外界面均达到极限侧摩阻力,则Ssi,Smi和Sci的表达式为
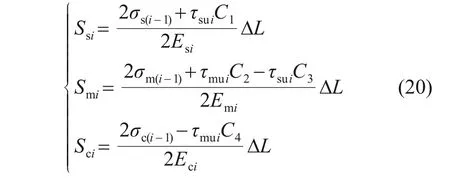
此外结合式(3)可得作用于砼芯、水泥土桩和桩周土第i个微元段底部的竖向应力σsi,σmi和σci分别为
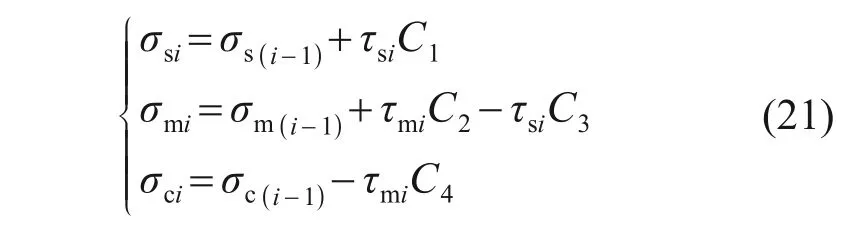
b.对于第1个微元段(i=1),首先假设其内、外界面侧摩阻力均未达到极限状态,基于步骤2)中假设的σc0,σm0和σs0,并结合式(13),(14)和(15)可求得该段砼芯、水泥土桩、桩周土的压缩量分别为Sc1,Sm1和Ss1;再根据式(21),求得相应竖向应力σc1,σm1和σs1。
c.对于第i个微元段(i>1),首先根据(i-1)段(上一个微元段)内、外界面的侧摩阻力形式假定该段界面侧摩阻力形式并在步骤a中选择对应的压缩量表达式进行计算。
例如,若第i-1个微元段的内、外界面均未达到极限状态,则假设第i个微元段的内、外界面也均未达到极限状态,结合式(13),(14),(15)和(21)求得第i个微元段砼芯、水泥土桩、桩周土的压缩量与竖向应力以及桩-土与砼芯-水泥土桩的相对位移si和mi。
d.将求得的第i个微元段的si和mi分别代入式(8)和(10)的判断条件中,检查预先假定的第i个微元段内、外界面的侧摩阻力形式是否正确。若正确,则继续计算第i+1个微元段的应力与变形;若不正确,则更换侧摩阻力形式并在步骤a中选择合适的计算方程并重复步骤c。
当i从1 迭代到nc后,即可得到复合桩段桩周土、水泥土桩和砼芯在各个深度处的压缩量、相对位移和应力。
4)在纯水泥土桩顶部(i=nc),桩周土应力连续,水泥土桩的竖向应力σM0为复合桩段底部砼芯和水泥土桩竖向应力σc(nc)和σm(nc)的加权平均值,其计算公式如下:
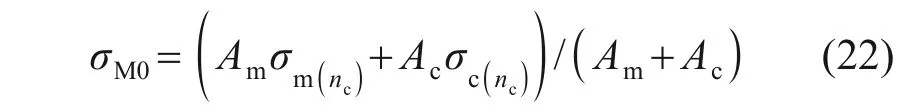
5)关于纯水泥土桩段应力与变形计算,以第i段(nc<i<n+1)为例,计算过程如下。
首先基于内、外界面侧摩阻力形式的假设(式(8)和(9)),将其分别代入式(4)和(7)中得到桩周土与水泥土桩第i个微元段的压缩量Ssi和Smi的2种不同形式的表达式。
若外界面未达到极限侧摩阻力,则Ssi和Smi的表达式为
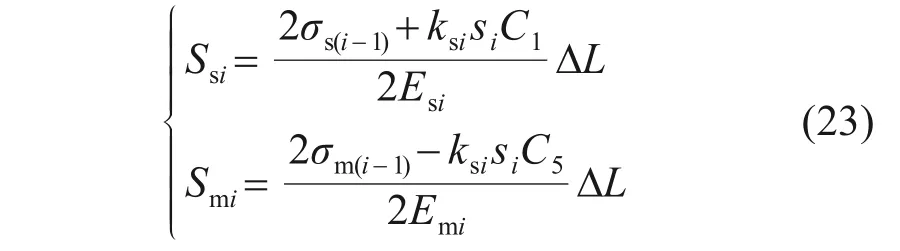
若外界面达到极限侧摩阻力,则Ssi和Smi的表达式为
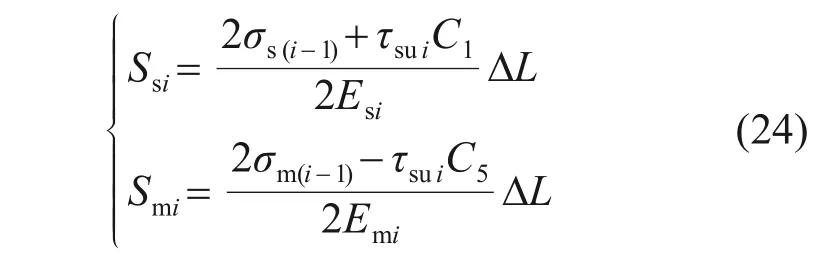
此外,结合式(5)可得到作用于水泥土桩、桩周土第i个微元段底部的竖向应力σmi和σsi表达式为
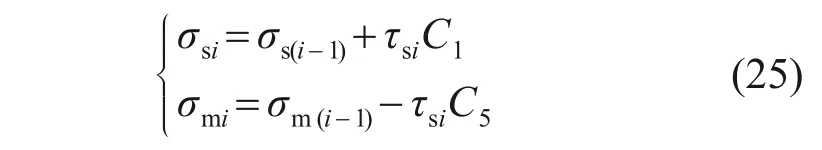
σmi和σsi具体迭代过程与步骤3)相似。
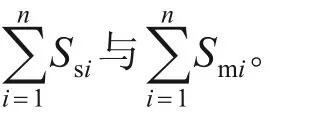
若
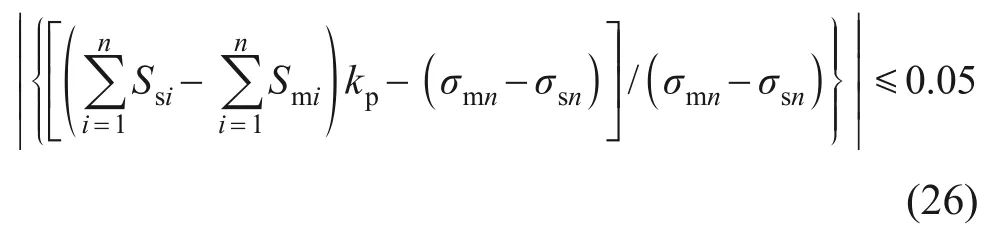
满足误差要求,则导出结果(其中kp为桩端土刚度系数);
若
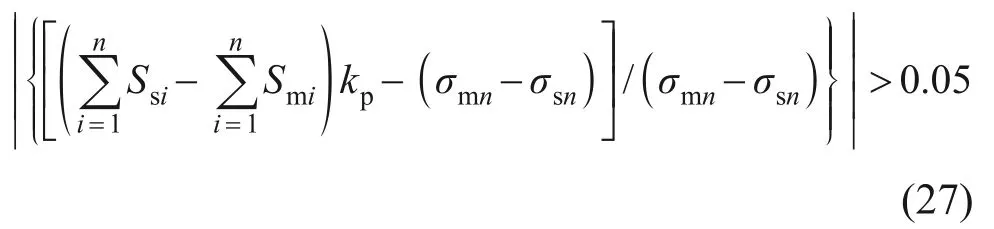
不满足误差要求,则返回步骤2)通过调整取值范围,对桩周土与水泥土桩的初始竖向应力σs0和σm0进行二维搜索,重新迭代计算,直到误差符合土木工程中对误差的要求(小于0.05)。
1.5 下卧层沉降计算
根据附加应力产生原因的不同,可将下卧层沉降分为两部分:1)由地表桩间土压力引起的沉降。由于地表桩间土压力是作用在土体表面的均布荷载,故其在下卧层产生的附加应力可由Boussinesq解求得;2)由桩侧阻力和端阻力引起的沉降。由于桩侧阻力和端阻力是作用在土体内部的荷载,故其在下卧层引起的附加应力可由Mindlin 解求得。确定附加应力之后,沉降便可以通过分层总和法计算得到:首先通过比较下卧层中某点的附加应力与自重应力的数量关系确定压缩层厚度,其次对下卧层进行分层,计算各土层的压缩量并求和,即可得到下卧层沉降。
2 参数选取
对于CDCM 桩外界面(即桩-土界面),基于理想弹塑性模型的假设,外界面的摩擦因数ks可以通过弹性理论计算得到[18]:
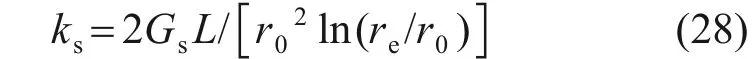
式中:Gs为桩周土体的剪切模量;re为影响半径;r0为桩身半径;ln(re/r0)通常可近似取4[19]。
对于内界面即砼芯-水泥土桩界面,结合试验结果和数值模拟结果[11],可取km=70~100 MPa/m。
桩端土刚度系数kp,可以通过下式估算得到[20]:
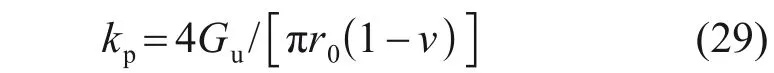
式中:Gu为桩端土体的剪切模量;ν为桩端土体的泊松比。
3 工程实例对比验证
为验证本文提出的刚性基础下CDCM 桩复合地基工作性状迭代分析法的合理性以及采用该法计算所得结果与实际工况的匹配度,选取某工程背景下的单桩复合地基进行平板静载实验,记录实验数据并绘制荷载-沉降曲线,最后将其与采用本文方法计算得到的荷载-沉降曲线进行对比验证。
该地基处理工程场地内普遍分布深厚淤泥或淤泥质土,厚度达到35~41 m,41 m深度以下为土性较好的砂土层。根据室内试验及原位测试,淤泥层含水量平均值达62%,孔隙比平均值为1.745,压缩系数高达1.50 MPa-1。
采用CDCM 桩对地基进行处理,CDCM 桩按等边三角形布置,桩间距为1.6 m,极限桩端阻力qu=1 000 kPa,km=100 MPa/m。地基处理范围内土层分布如下:[0,22.0)m是淤泥层,[22.0,33.5)m是淤泥质土层。CDCM桩身参数及土层参数分别如表1和表2所示。
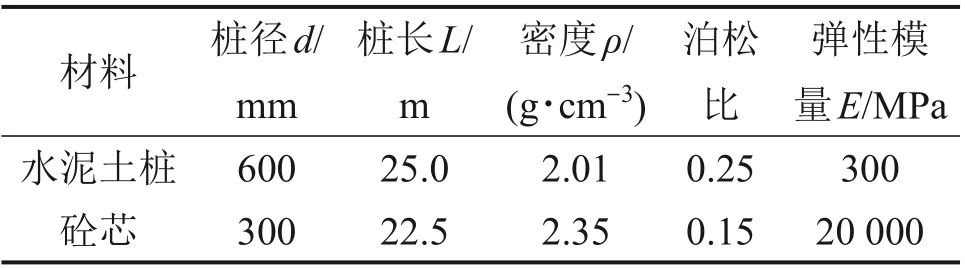
表1 水泥土桩、砼芯参数Table 1 DCM pile and concrete core pile parameters
选取单桩复合地基进行静载平板实验,圆形载荷板面积为2.2 m2(直径约为1.65 m),可看作刚性基础且桩顶无垫层。通过载荷板向桩顶逐级加载,得到荷载-沉降曲线。将不同方法所得荷载-沉降曲线进行对比,结果如图4所示。
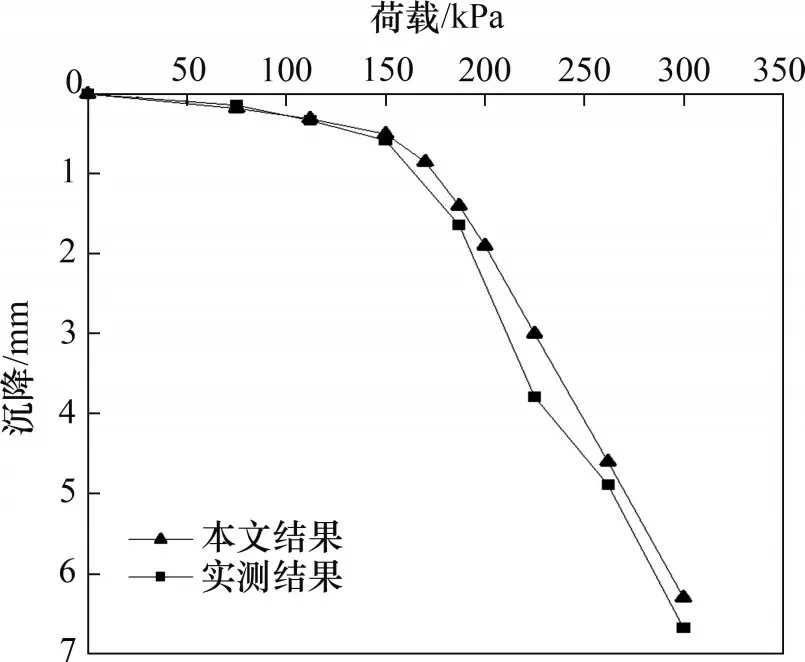
图4 不同方法所得荷载-沉降曲线对比Fig.4 Comparison of load-settlement curves obtained by different methods
由图4可知:虽然计算结果和实测结果有一定的差距,但是二者整体趋势一致,并且计算与实测极限承载力也比较接近,因此可认为本文提出的刚性基础下CDCM 桩复合地基工作性状迭代分析法是可靠的。
4 CDCM桩复合地基工作性状分析
选取标准算例参数如下:CDCM 桩中砼芯半径rc为125 mm,芯长Lc为7.5 m;水泥土桩半径rm为350 mm,桩长L为12.5 m;桩间距为1.8 m;面积置换率为12%;极限桩端阻力qu=1 000 kPa,km=70 MPa/m,荷载为150 kPa,土层参数如表3所示。

表3 土层参数Table 3 Soil parameters
4.1 桩身轴向应力
刚性基础下CDCM 桩复合地基中砼芯与水泥土桩的竖向应力随深度的变化如图5 所示。由图5(a)可知:砼芯竖向应力随着深度增大而逐渐减小,最大应力位于桩顶处。此外,在地基浅部,应力减小幅度较小;随着深度增加,应力减小幅度逐渐增大。由图5(b)可知:水泥土桩竖向应力整体变化趋势表现为先增大后减小,且在砼芯底部出现应力突增的现象,这与周佳锦等[2]通过室内模型试验得到的结论相吻合。这种应力“突增效应”可能会导致砼芯底部的水泥土产生受压破坏,因此,在实际工程设计中应适当提高该区域水泥土强度。在复合桩段,水泥土桩主要承受内、外界面两个方向相反的侧摩阻力,竖向荷载分担较少,其中内界面侧摩阻力向下,外界面侧摩阻力向上,因此水泥土桩应力的变化规律取决于内、外界面侧摩阻力的发挥情况。
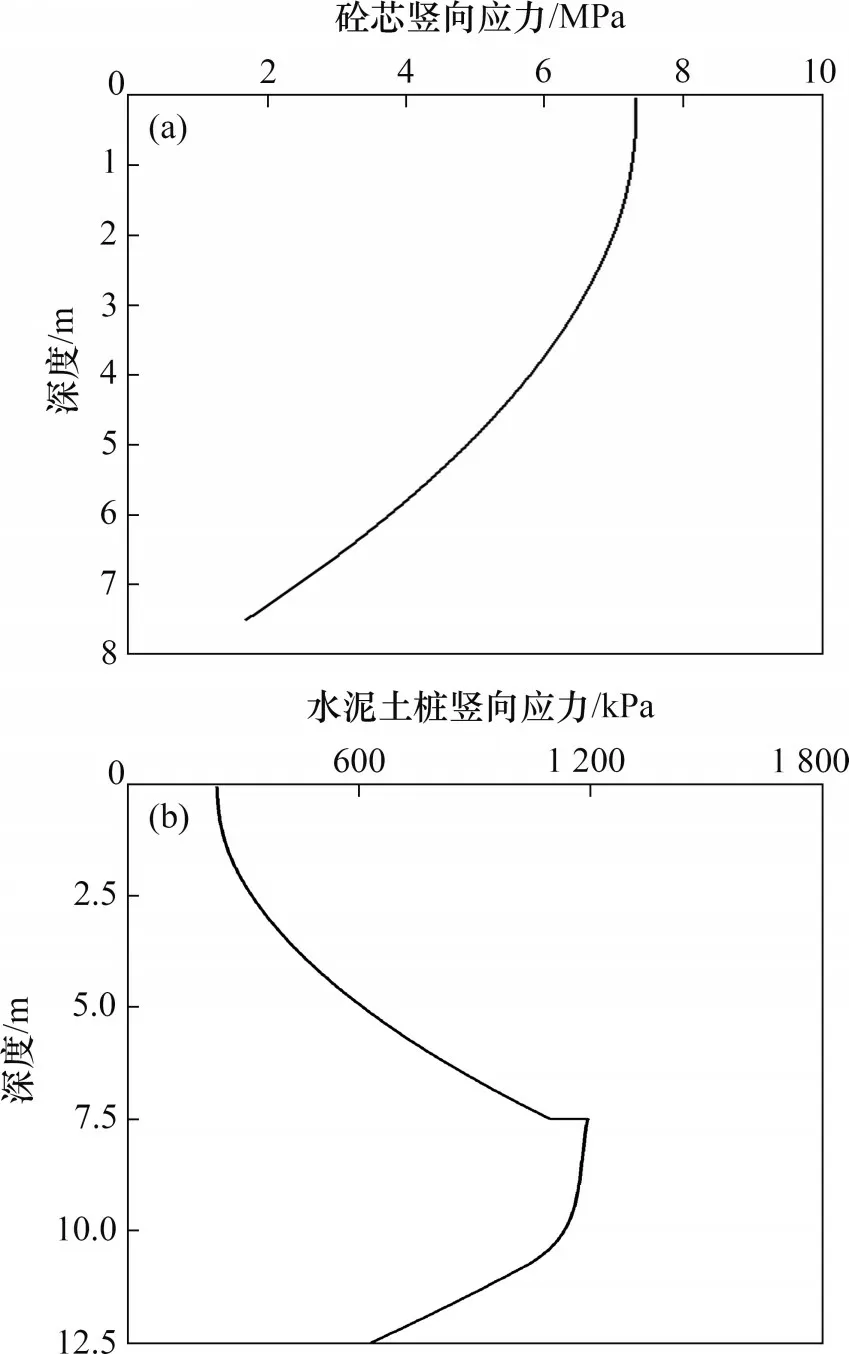
图5 桩身竖向应力随深度的变化Fig.5 Variations of vertical stress of pile shaft with depth
4.2 侧摩阻力
CDCM 桩内、外界面侧摩阻力随深度的变化如图6 所示。由图6(a)可以看出:砼芯-水泥土桩(内)界面侧摩阻力整体是逐渐增大的,在z=3.2 m深度处,界面侧摩阻力完全发挥。
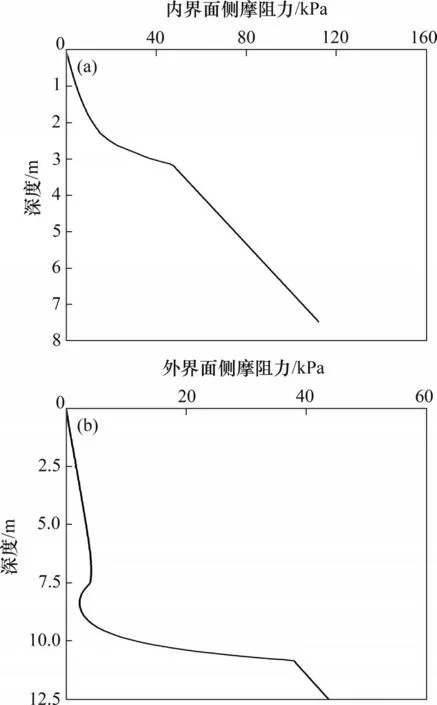
图6 侧摩阻力随深度的变化Fig.6 Variations of skin friction with depth
由图6(b)可以看出:桩-土(外)界面侧摩阻力整体较小,这是因为水泥土桩侧表面积较大,在传递荷载中起到扩散作用,因此外界面侧摩阻力比内界面的小。整体上外界面侧摩阻力沿深度逐渐增大,但在砼芯底部会小范围减小,这是因为在砼芯长度以下,由水泥土桩承担竖向荷载,而这部分桩与桩周土的弹性模量相差较小,属于柔性桩范畴,所以桩侧摩阻力小范围减小,超过这一范围后桩侧摩阻力沿深度方向逐渐增大并在z=11 m深度处达到极限侧摩阻力后持续增加。
结合图6(a)和(b)可知:相较于外界面,内界面侧摩阻力更早达到极限并完全发挥。
4.3 荷载分担比
当上部荷载变化时,砼芯、水泥土桩以及桩周土的荷载分担比变化情况如图7所示。由图7可见:1) 在标准算例即150 kPa 荷载的作用下,砼芯、水泥土桩和桩周土的荷载分担比分别为74%,16% 和10%;2) 当上部荷载从50 kPa 增大到250 kPa 时,砼芯、水泥土桩和桩周土的荷载分担比变化范围分别为61%~81%,13%~19%和6%~20%,其中砼芯承担了大部分上部荷载;3)随着上部荷载增加,砼芯的荷载分担比降低,水泥土桩和砼芯的荷载分担逐渐增大。这是因为随着荷载水平的提高,复合地基的变形加剧,砼芯、水泥土桩以及桩、土间的相对位移增加,侧摩阻力逐渐发挥,由砼芯传递给水泥土桩与桩周土的荷载增大,因此砼芯的荷载分担比随之减小。
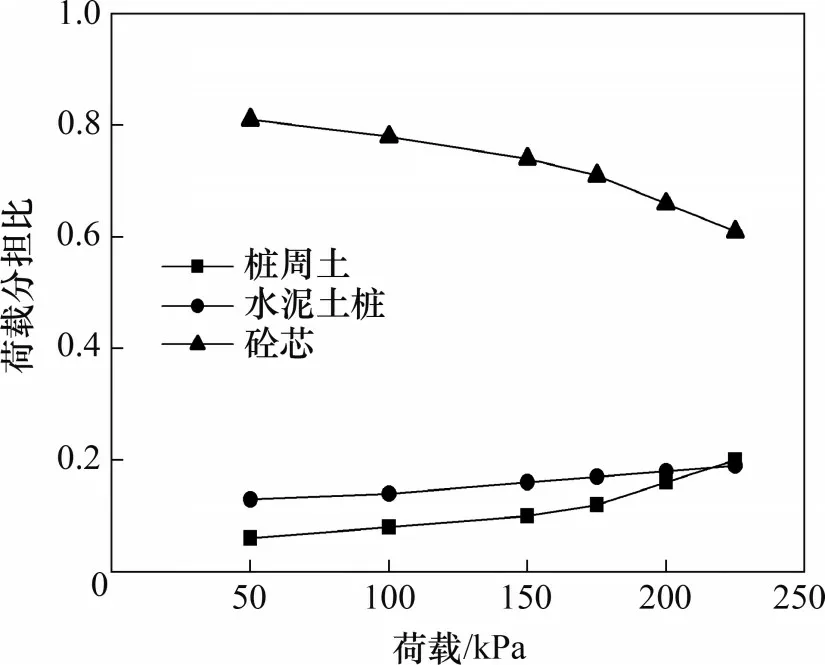
图7 荷载分担比随荷载水平的变化曲线Fig.7 Variations of load distribution with load from rigid foundation
5 CDCM桩复合地基工作性状的影响因素分析
基于第4 节中的基本算例,通过改变CDCM桩的参数,研究含芯率、芯长比、面积置换率和荷载水平等因素对复合地基桩土应力比(桩顶处砼芯和水泥土桩按面积比换算的平均应力与桩周土应力的比值)和复合地基沉降的影响规律。其中,CDCM桩复合地基的沉降为复合桩(有砼芯)段、水泥土桩(无砼芯)段和下卧层三部分压缩量之和。
5.1 含芯率
含芯率(砼芯与CDCM桩截面积之比)对CDCM桩复合地基桩土应力比的影响如图8(a)所示。由图8(a)可见:随着含芯率增大,平均桩土应力比由54.4 近似呈线性增大至239.9。这是因为,随着含芯率增大,复合桩的弹性模量提高,荷载分担比增加,平均桩土应力比也随之增大。
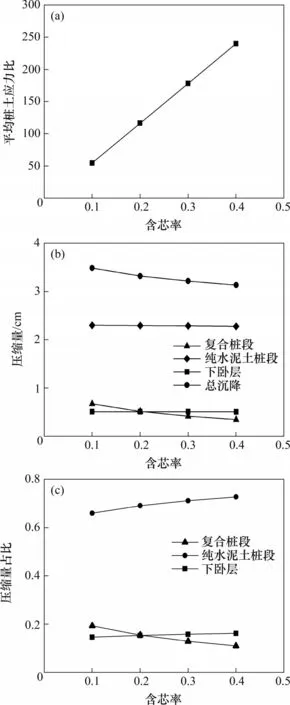
图8 含芯率对复合地基工作性状的影响Fig.8 Influence of area ratio of core concrete pile and cemented soil on working behaviors of composite foundation
含芯率对CDCM 桩复合地基压缩量的影响如图8(b)所示。由图8(b)可知:当含芯率从0.1 增加到0.4,复合桩段压缩量从0.67 cm减少到0.35 cm;纯水泥土桩段与下卧层压缩量变化不明显;复合地基总沉降从3.49 cm 减小到3.13 cm,降低了10.3%,说明含芯率对CDCM桩复合地基沉降的影响不大。
由图8(c)可知,随着含芯率从0.1 增加到0.4,复合桩段压缩量占比从19.3%减少到11.0%,纯水泥土桩端压缩量占比从66.0%增加到71.0%,且下卧层压缩量占比从14.7%增加至16.3%,说明随着含芯率增加,复合桩段压缩量占比减小,纯水泥土段和下卧层压缩量占比有所增大;且复合地基沉降主要发生在纯水泥土桩段,这与桩端土层性质较好的结论是一致的。
5.2 芯长比
芯长比(砼芯与CDCM 桩长度之比)对CDCM桩复合地基桩土应力比的影响如图9(a)所示。由图9(a)可知:随着芯长比增大,平均桩土应力比逐渐增大,当芯长比从0.5 增加到1.0 时,平均桩土应力比从54.4 增加到141.0,但增幅逐渐减缓。由此可见砼芯长度增加会使荷载逐渐向桩身集中。
图9(b)所示为芯长比对砼芯底部水泥土桩竖向应力的影响,由图9(b)可知:当芯长比从0.5 增大到1.0时,水泥土桩突变前的竖向应力从748.8 kPa减小到463.2 kPa;突变后的竖向应力从801.0 kPa减小到463.2 kPa,且突变幅度也随芯长比增加而减小。
芯长比对CDCM 桩复合地基沉降的影响如图9(c)所示。由图9(c)可见:当芯长比从0.5 增大到1.0时,复合桩段压缩量从0.55 cm增加到0.90 cm,略有增加;纯水泥土桩段压缩量从2.84 cm减小到0 cm(芯长比为1.0 时纯水泥土桩段长度为0 cm)且降速较快;下卧层则由于附加应力有所增加,表现为压缩量略有增大。复合地基的总沉降从3.91 cm显著减小到1.45 cm,降低了62.7%。
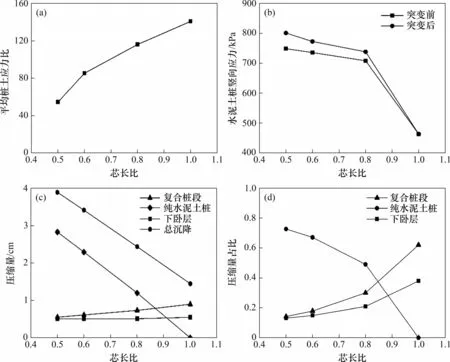
图9 芯长比对复合地基工作性状的影响Fig.9 Influence of length ratio of core concrete pile and cemented soil on working behaviors of composite foundation
由图9(d)可知:当芯长比从0.5 增加到1.0 时,复合桩段压缩量占比(即压缩量与总沉降之比)从14%增加到62%;纯水泥土桩段压缩量占比从73%加速下降到0;下卧层压缩量占比从13%增加到38%。
综上可知,芯长比对复合地基的沉降有较大影响:随着芯长比增大,复合地基沉降的主要发生区域即纯水泥土桩段长度缩短且竖向应力降低,复合地基沉降显著减小。因此,增加砼芯长度是控制CDCM桩复合地基沉降的有效手段。
5.3 面积置换率
面积置换率(CDCM 桩截面积与其影响范围内复合地基面积之比)对CDCM桩复合地基桩土应力比的影响如图10(a)所示。由图10(a)可见:随着面积置换率增大,平均桩土应力比降低,当面积置换率从0.08 增加到0.20 时,平均桩土应力比从103.5降低到69.1,但降低幅度逐渐减小。
面积置换率对CDCM 桩复合地基沉降的影响如图10(b)所示。由图10(b)可见:当面积置换率从0.08 增加到0.20 时,复合桩段压缩量从1.15 cm 减小到0.33 cm,降低了71.3%;纯水泥土桩段压缩量从3.12 cm 减小到1.50 cm,降低了51.9%;下卧层沉降量从0.56 cm 减小到0.35 cm,降低了37.5%。总沉降量从4.83 cm 减小到2.17 cm,降低了55.1%。这是因为,随着面积置换率增大,桩间距减小,复合地基上部总荷载减少,所以下卧层、复合桩段以及纯水泥土桩段压缩量减小,总沉降减小。
由图10(c)可知:当面积置换率从0.08 增加到0.20 时,复合桩段的压缩量占比从24%减小到15%,纯水泥土桩段压缩量占比从65%增加到69%,下卧层压缩量占比略有增加。这说明纯水泥土桩段压缩量在总沉降中占比最大,但面积置换率变化对复合桩段压缩量占比的影响更大。
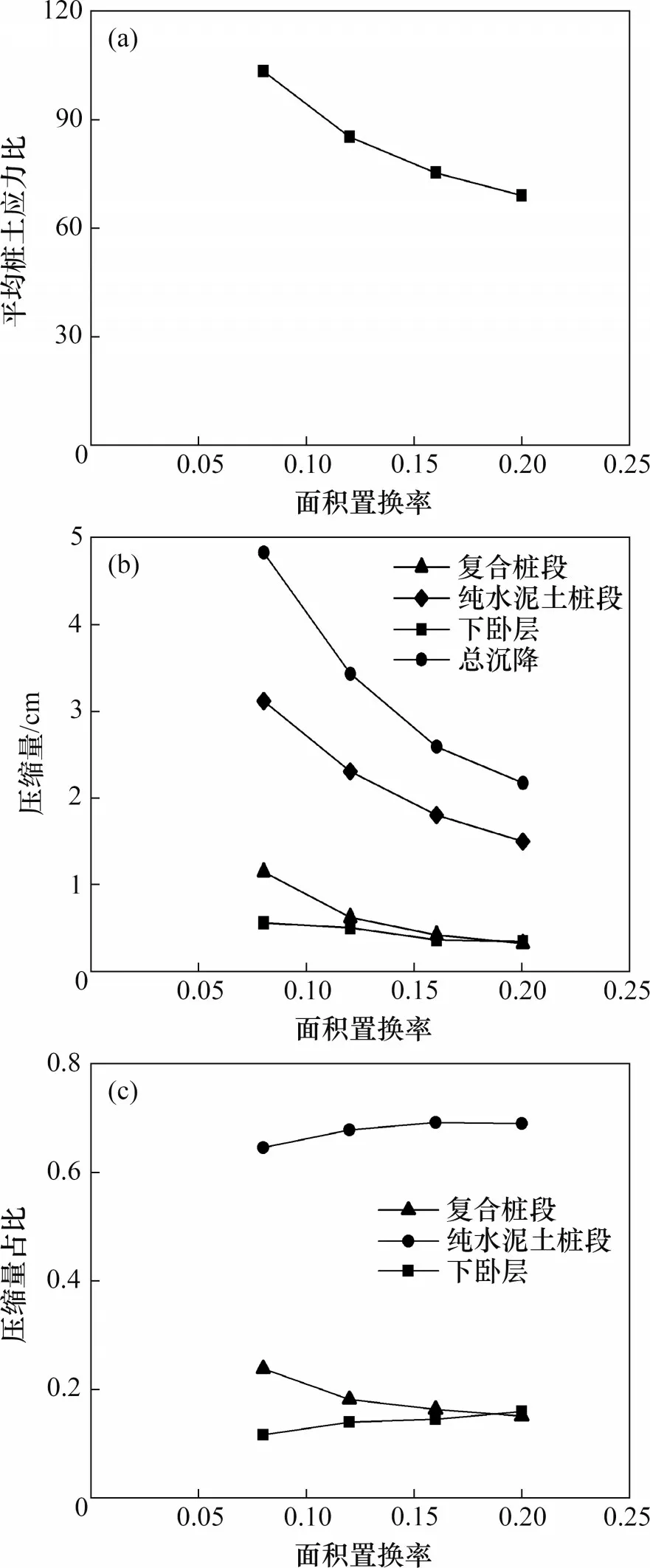
图10 面积置换率对复合地基工作性状的影响Fig.10 Influences of area replacement ratio on working behaviors of composite foundation
5.4 荷载水平
荷载水平对CDCM 桩复合地基桩土应力比的影响如图11(a)所示。由图11(a)可见:随着荷载增加,平均桩土应力比逐渐减小,当荷载从50 kPa增加到200 kPa 时,平均桩土应力比从116.2 降低到38.9,说明随着上部荷载增加,复合地基中变形增加,内外界面侧摩阻力逐渐发挥,促进了桩土之间的荷载传递,桩身应力逐步向桩间土转移,平均桩土应力比降低。
荷载水平对CDCM 桩复合地基沉降的影响如图11(b)所示。由图11(b)可见:当上部荷载从50 kPa 增加到200 kPa 时,复合桩段压缩量从0.27 cm 增加到1.97 cm,纯水泥土桩段压缩量从1.05 cm 增加到5.32 cm,下卧层压缩量从0.12 cm增加到1.02 cm,总沉降从1.44 cm增大到8.10 cm,说明荷载水平对复合地基各组分的压缩量和总沉降的影响较大。
由图11(c)可知:当上部荷载从50 kPa 增加到200 kPa 时,复合桩段压缩量占比从15%增加到26%;纯水泥土桩段压缩量占比从72%减小到63%,下卧层压缩量占比从13%减小到11%。说明随着荷载水平增加,复合桩段压缩量占比增大。
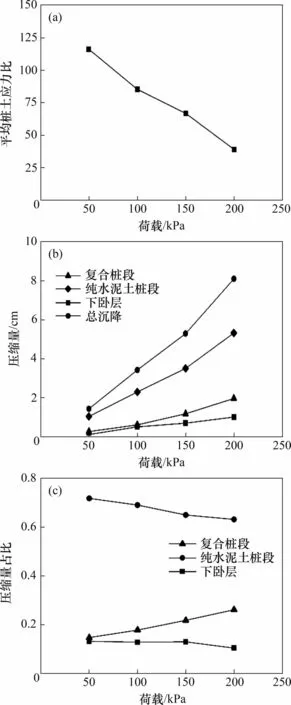
图11 荷载对复合地基工作性状的影响Fig.11 Influence of load from rigid foundation on working behaviors of composite foundation
6 结论
1)提出了一种刚性基础下砼芯水泥土复合桩的工作性状分析方法,该法考虑地基土分层和砼芯与水泥土桩长度不等的情况,所得结果与实际工程的现场实测结果较为吻合。
2)在砼芯底部水泥土桩身应力会产生“突增效应”,存在水泥土受压破坏的可能,在设计和施工中应予以重视。
3)含芯率、芯长比、面积置换率以及上部荷载水平都会对复合地基的工作性状产生较大影响,且含芯率、芯长比与桩土应力比呈正相关,面积置换率、荷载水平与桩土应力比呈负相关。
4)复合地基总沉降中纯水泥土桩段压缩量占比较大,且受芯长比、面积置换率以及荷载水平变化影响较大,故可通过增加砼芯长度来控制CDCM桩复合地基的沉降。

