可换层四向穿梭车仓储系统的I/O站台位置研究
张新艳 孙朝阳
(同济大学 机械与能源工程学院 上海 201800)
1 引言
传统堆垛式自动化立体仓储系统(Automated Storageand Retrieval System, AS/RS)设备利用率低,难以灵活部署,难以满足现代物流的需求。作为自动车辆存储系统(Autonomous Vehicle Storage and Retrieval System, AVS/RS)的一类变种,四向穿梭车仓储通过水平自动的穿梭车和垂直移动的提升机完成出入库任务,提高了系统的作业效率和柔性,以及仓储作业调度的快响应要求[1]。
关于四向穿梭车仓储系统的研究尚不多,目前主要研究 AVS/RS系统。例如,Roy、Ning等[2-3]使用仿真模型研究了AVS/RS的系统吞吐量的影响以及多种设备配置下的出库任务周期。HERAGU、FUKUNARI等[4-5]采用开环排队网络和闭环排队网络对AVS/RS 系统进行建模,计算了系统的出入库周期时间和设备利用率。EKREN等[6-7]建立了半开环排队网络模型并使用AMVA和MGA两种方法求解AVS/RS 系统的任务周期与设备利用率。
目前的研究尚有需深入或补充之处,主要包括:(1)相对于对运作策略方面的研究,针对AVS/RS系统布局方面的研究较少,尤其针对其中的I/O站台位置的详细研究尚不多见。(2)不同仓库类型、不同运作策略下仓储系统的作业流程不同,无法使用相同的排队模型。
针对以上问题,本文以可换层的四向穿梭车仓储系统为研究对象,构建了穿梭车LU驻留点策略下系统的半开环排队网络模型并通过 AMVA方法对出入库任务周期和设备利用率进行求解。
2 问题描述
2.1 四向穿梭车系统介绍
可换层的四向穿梭车仓储系统由立体货架、四向穿梭车、提升机、出入库站台(I/O站台)和输送系统组成,具体布局如图1所示。

图1 可换层的四向穿梭车仓储系统示意图
在四向穿梭车仓储系统中,四向穿梭车负责水平方向的移动与拿取或放下货物;提升机负责携带穿梭车将其运送至不同的货层;出入库站台与输送系统相连,用于将出库货物放置到输送系统,或从输送系统接受入库货物;输送系统指连接仓储部分和分拣部分的传送带。每一层货架中穿梭车请求提升机的位置被称为LU(Loadand Unload)站台,该站台是穿梭车进入和离开提升机的位置,其位置在提升机轨道与该层货架跨巷道通道的交叉点处。
2.2 出入库任务流程
可换层的四向穿梭车仓储系统需要提升机和穿梭机相互配合才能完成出库和入库任务,出入库的流程较为相似,如下所述:
1)将作业任务分配给穿梭车
作业任务到达系统后需将其分配给空闲的四向穿梭车,若系统中有空闲的穿梭车,则该任务分配成功;若此时不存在空闲的穿梭车,则该任务进入等待队列直到有穿梭车变为可用状态。
2)穿梭车拿取货物
穿梭车运行至 I/O 站台(入库任务)或目标货位(出库任务)拿取货物。这一过程需判断穿梭车当前位置与目标货位位置,并根据货位所处层与穿梭车所在层决定是否需要跨巷道作业和换层作业。
3)穿梭车取货后送到指定位置完成卸货
对于出库任务,穿梭车需运行至I/O站台卸下货物;对于入库任务,穿梭车需携带货物到达指定货位卸下货物。该过程也需要根据穿梭车位置与目标位置决定是否需要跨巷道作业和换层作业。
3 数学建模与求解
3.1 系统假设
为建立合理可信的四向穿梭车出入库模型,需对模型信息和假设进行说明。考虑以托盘为存取单元的可换层四向穿梭车仓储系统。提升机采用结束点停留策略(Point of Service Completion, POSC)即停留在任务结束的地方;穿梭车采取LU驻留点策略即完成任务后行驶至当前层LU站台旁的缓冲区。模型的其他假设如下:(1)货物为随机存储;(2)货架及货物的规格相同,不考虑重量对于穿梭车和提升机的影响;(3)各设备的加减速阶段的加速度恒定;(4)穿梭车转向时间固定,穿梭车拿取货物的时间固定;(5)订单类型与目标货位随机产生;(6)任务分配和设备调度适用 FCFS(First-Come First-Served)规则;(7)不考虑穿梭车的互锁和堵塞现象;(8)以一台提升机配合多条巷道为一个研究单元。
3.2 排队网络模型
排队网络模型是一种针对随机离散事件的常用动态系统模型。为了贴近实际情况,使用半开环排队网络模型构建四向穿梭车仓储系统模型。模型不考虑输送系统与分拣系统,将提升机建为单服务台节点,将穿梭车建为多服务台节点,得到的排队模型如图2所示。后续分析涉及的其他参数及含义如表1所示。

图2 四向穿梭车系统半开环排队网络模型

表1 系统参数及含义
3.3 服务时间计算
3.3.1 设备运行规律
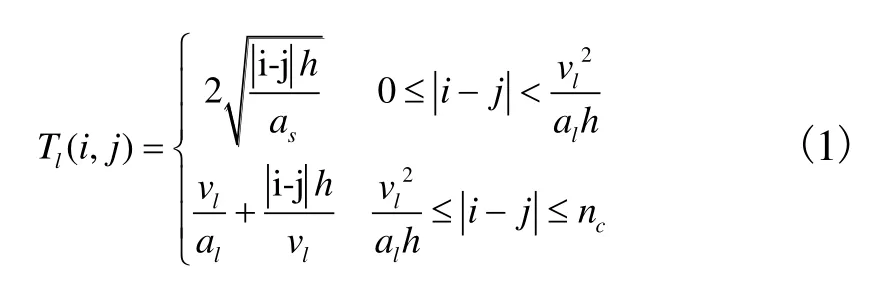
3.3.2 穿梭车节点服务时间计算
排队网络模型的求解需计算各节点的服务时间。穿梭车节点的服务时间包括穿梭车的单独移动过程与取/放货物的过程。以穿梭车从LU站台运行至同层目标货位这一过程为例,计算预期花费时间Tes如式(2)所示。

随机存储策略下在跨巷道通道上移动所花费的平均时间为

同理,在本层内巷道方向上从巷道起点至目标货位所花费的平均时间为

3.3.3 提升机节点服务时间计算
不同情形下穿梭车完成任务需跨越的层数不同,提升机的运动距离也不相同,依据任务类型、接取任务的穿梭车所在层数、出/入库货位所在层数,将所有作业流程共分为九种情况。
为计算各情况的发生概率,需明确出入库任务的概率与接取任务的穿梭车处在各层的概率。假设出库与入库订单到达的泊松分布参数为λr和λs,因此,任务队列中下一个任务是入库(出库)任务的概率为(出库)。在此基础上,穿梭车采用了LU站台驻留点策略,因此穿梭车完成任务后停留在每一层的概率如式(5)所示,这也是新任务分配给空闲穿梭车时该穿梭车所在层的概率。


表2 出入库任务各情况发生概率表
得到各情况的发生概率后,还需对每一种情况分别计算提升机的运行距离。穿梭车每次请求提升机时,提升机完成本次请求的过程分为四部分:提升机从驻留点运行至穿梭车层;穿梭车进入提升机;提升机携带穿梭车到达指定层;穿梭车离开提升机。为得到各情况下提升机的运行距离,首先计算提升机空闲时停留在各层的概率,如式(6)所示。

随后,根据随机存储策略,出入库任务的目标货位在各层的概率相同,得到的各情形提升机预期服务时间如表3所示。

表3 不同情况下提升机的预期服务时间
3.4 排队模型求解
根据Buitenhek[8]的建议,求解该排队网络参数使用以下方法:
(1)删除同步节点,将半开环排队网络整合为闭环排队网络。使用AMVA(Approximate Mean Value Analysis)方法,对该闭环排队网络进行分析,最终得到该闭环排队网络的效率记为τCQN1。
(2)将同步节点换为与负载有关的单服务台节点,形成一个新的闭环排队网络,并将该新节点作为节点。同样使用AMVA方法对该闭环排队网络网络进行求解,可得该网络的效率与各节点的排队长度,分别记为τCQN2和ELm(n)。
(3)使用生灭过程对M+1节点进行单独分析,并得到M+1节点的平均队长。
(4)计算最终数据。对于该排队模型,较为关心的指标是穿梭车的利用率ρs、提升机的利用率ρi以及完成出入库任务的平均时间tCT。利用三步求解过程中得到的数据,系统各指标的计算公式如(8)~(11)所示。其中,ELs为同步节点处的期望队长,vi指提升机节点的访问比例,ESi指提升机节点的平均服务时间,ELt代表除节点外其他M+1节点的期望队长之和。

4 实验与分析
4.1 模型验证
为了验证排队模型的准确性,使用python搭建了四向穿梭车仓储系统的仿真模型。使用理论模型与仿真模型在多种水平下进行了多次试验。使用的系统参数如表4所示。

表4 系统参数表

(接表4)
对不同任务到达率水平进行测试,排队论模型按上文方法求解,仿真模型模拟时间为300小时,每个案例进行50次重复取平均值。最终得到的误差结果如表5所示,其中相对误差为理论模型数据与仿真模型数据的差值再与仿真模型数据的比值。

表5 排队论模型与仿真模型数据对比
从表5可以看出,在多种参数的实验下,排队论模型得到的提升机利用率同仿真模型得到的数据的误差值始终维持在较低的水平。在穿梭车利用率和任务完成时间指标上二者差距较大,这主要是模型聚合导致的。
三种指标的相对误差始终维持在10%以内,能够证明排队论模型能够较好地反应现实情况,是足够可信的。
4.2 I/O站台位置分析
为详细测定I/O站台位置对系统效率的影响,以单元中所有巷道与跨巷道通道的交叉点为I/O站台的可放置范围,参考实际仓库规模:有11层3巷道5辆穿梭车和8层6巷道5辆穿梭车两种仓库以及每小时100、90个订单两种订单到达速率,对这4种情况分别改变I/O站台的位置进行理论模型求解,所得的结果如表6所示。

(接表6)
系统的其他参数与表4相同。由于呈对称关系的I/O站台位置所得数据相同,仓库中将I/O站台设置在1层1巷道或11层1巷道,因此仅需计算约四分之一的数据。
可以看出,在两种仓库以及不同的任务到达速率下,I/O站台的位置均会对任务完成周期产生较大影响。I/O站台的位置越靠近提升机与跨巷道通道决定的平面的中心点,系统的任务完成周期越短。对于层数为偶数的仓库,最优的I/O站台高度位于中心点的下方货层。通过更加详细的数据对比,相比于通常将I/O站台的位置设置在矩形中心点正下方的底层货架处,更靠近中心点的I/O位置能够为系统带来约6%~14%的效率提升。从同一种仓库不同任务到达速率的数据中还可以发现,任务到达速率越快时,I/O位置变动对任务完成周期的影响越大。由此可见,调整I/O站台的位置对于用于电商等任务到达速率波动大的仓库是一种解决波动的成本更小、也更稳定的做法。
5 结语
本文针对托盘运输的可换层四向穿梭车仓储系统,建立了穿梭车LU驻留点策略下仓储系统作业流程的半开环排队网络模型,并通过AMVA方法对出入库任务周期及设备利用率进行了求解。与仿真模型的对比表明该排队模型能够较准确地计算系统指标。随后,使用该排队模型分析两个实际应用的仓库在不同任务达到速率情况下不同I/O站台位置对任务周期时间和各设备利用率的影响。通过分析,I/O站台以单元中提升机与跨巷道通道决定的平面的中心点为最佳,若单元内巷道数或层数为偶数,则以最接近中心点的位置为最佳。与通常将I/O站台设置在中心点正下方的底层布局相比,靠近中心点可以减小约6%~14%的任务周期时间,能够提高仓储系统的运作效率。

