基于动力学分形分析的磨削在线监测研究

汪学栋 胡育佳

（1.上海机床厂有限公司 上海 200093；2.上海理工大学 机械工程学院 上海 200093）

1 引言

零件加工质量是保证机械产品质量的基础。表面粗糙度是表征加工质量的重要参数，而对其进行检测是工厂评判外圆磨床加工精度的重要手段。目前零件表面粗糙度检测的传统方法大多数选择离线检测，主要依赖于一些专用测量仪器对加工完成后的零件表面粗糙度进行测量。传统离线检测方法效率低、成本高且不能实时反馈加工信息，技术人员不能通过反馈信息实时发现加工中存在的问题并且对问题进行修正，这使得加工质量不能得到总体的提高，加工质量很难达到预期目标。但是通过粗糙度的在线监测可以实时掌握零件表面的质量状况，并调整工艺参数控制零件表面质量，保证其质量达到预期目标。

目前部分研究者研究了分形维数与零件表面粗糙度间的关联，李成贵[1]等人研究了分形数与表面粗糙度判定参数Ra和λa之间的关系，在此基础上李丽娜[2]等人通过采集设备加工零件时的振动信号，并对其进行分形维数的计算，发现盒维数对高频振动信号有明显反应，由此可以反应表面粗糙度。李浩[3]等人通过对轮廓仪测得的表面粗糙度，以及压电式振动传感器测得的振动信号进行处理，得到了其与表面粗糙度的对应关系。

本文基于分形理论可以提取振动特征的原理，将振动特征信号与磨床加工状态之间建立对应关系，通过提取磨削加工过程中外圆磨床关键部件的动态信号，并以其分形维数作为表面粗糙度的检测参数，建立外圆磨床表面粗糙度实时监测试验平台。通过研究不同位置的分形维数，发现识别结果具有一致性，证实了该动态测试方案对信号分形维数提取位置要求不高，可操作性强，有利于后续粗糙度在线监测的施行。

2 分形及其盒维数的计算

分形原指在自然界中普遍存在、不规则、破碎的物体，Mandelbrot给出更广泛、通俗的定义：局部与整体具有某种相似的形，称之为分形[4-7]。近年来分形技术被广泛应用于动力学特性分析、流体力学分析以及电化学反应等领域[8-9]。

满足一定条件的动力学系统会产生分形，判断形体是否分形，实际上判断其无标度区间是否存在即可。设平面R2内有图形F，在平面内作间距为δ的方格网，则F与方格网相交的方格数Nδ(F)称为图形F在标度（分辨率）δ下的盒数。

对于现实的无规则分形，通常盒维数只在特定的标度范围内存在。比如离散点组成的波形，δ大于等于1，且只能为整数。当在标度范围(δ1, δ2)内logNδ(F)与logδ能保持大约恒定的斜率时，此区间即为无标度区间[7,10]。在无标度区间(δ1, δ2)内，该形体可被视为分形，盒维数存在且其定义可修改为

对于M个采样点构成的振动波形{t ,f(t): a≤t＜b}，确定其无标度区间步骤如下（若f(t)存在负值，可统一加上一个常数形成正值来简化求总盒维数，该步骤不会对波形的形状及复杂程度造成影响）。

选择标度δ，将平面 (t,f(t))等分成间距格，横轴坐标被分成M/δ-1个等间距格[(m-1)δ+1，mδ+1]，m=1,…, M / δ -1；当δ≠1 时，采样点M- δ +1会到采样点M 的格子[M-δ+1, M]。

在横轴的第m区间内，用波形的最高值除以标度δ后的整数部分a减去波形的最低值除以标度δ后的整数部分b，得到的差值绝对值即为区间内波形与网格相交的盒数目。值得注意的是，最高值除以δ后余数不为0时，盒数目要加上1，其表达式为：

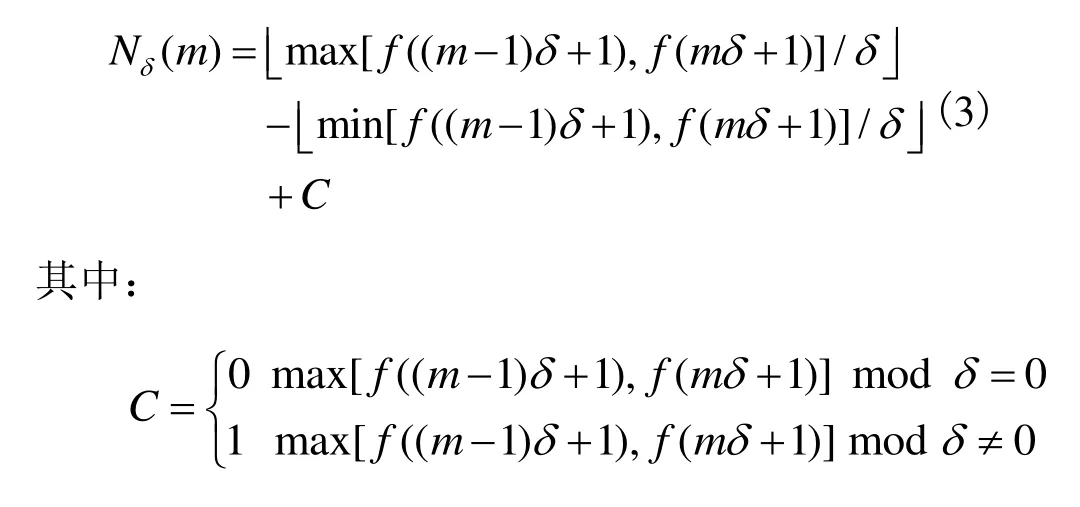
将所有区间的盒数目加起来，得到全局波形与网格相交的总盒数为：

取不同的标度δ，重复上述步骤得到相应Nδ(F)，得出Nδ(F)～δ的双对数曲线，该曲线的形状与振动频谱分布相关，包含振动的大量信息，当曲线中存在一段直线或近似直线，即该段区间(δ1, δ2)为无标度区间，可以判定波形F为分形，其盒维数为该段直线的平均斜率。

盒维数计算方法流程如图1所示。

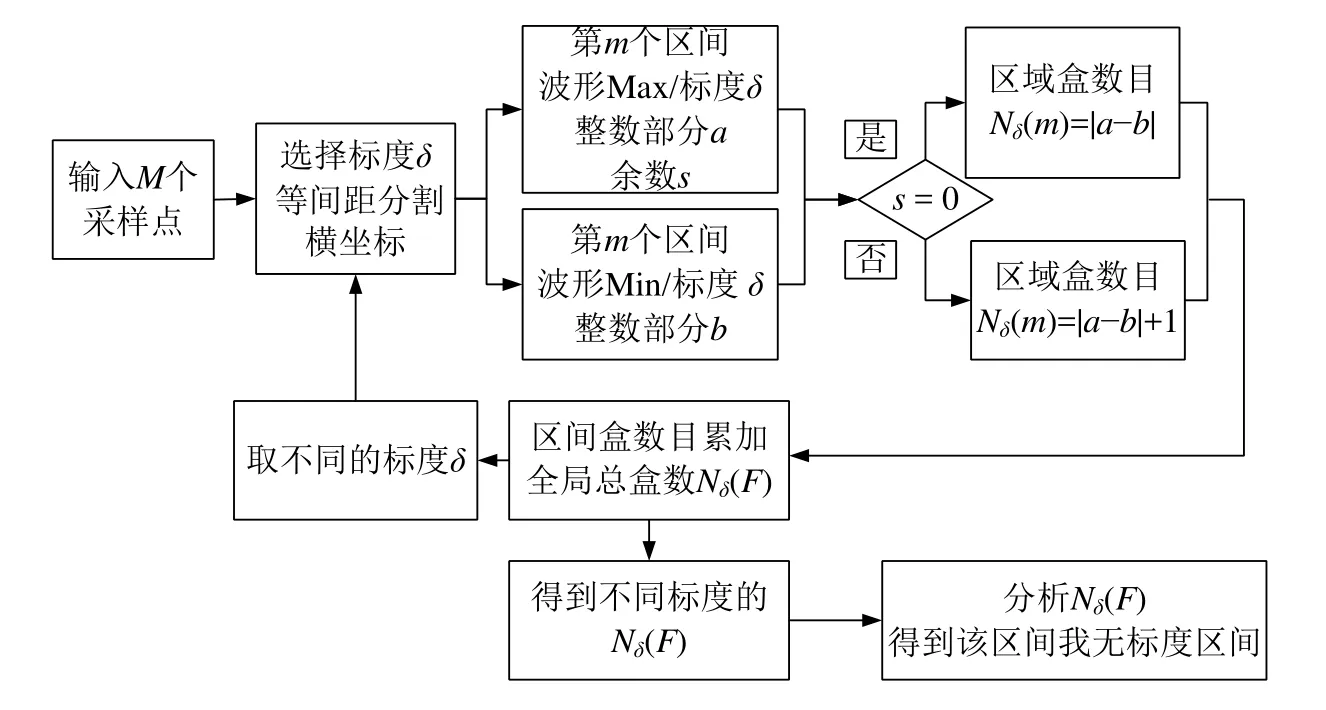
图1 盒维数计算方法流程图

3 磨削加工表面粗糙度监测实验

为验证基于分形理论的粗糙度在线监测方案的可行性，本文进行了轴承钢表面粗糙度实时监测试验，采用加速度传感器实时采集外圆磨床磨削过程中的加速度数据，计算振动信号中分形维数[11]，通过与粗糙度测量仪的测量结果进行对比，成功实现了粗糙度的实时监测。本文选取的待测试对象为外圆磨床关键部件，分别为头架、尾架、砂轮架、床身，各个部件设一个测试点。该实验选用的测试设备为加速度传感器，以及表面粗糙度测量仪。实验将在相同的磨削加工环境中，依次加工4根同批次的直径为Φ100 mm长度为500 mm的GCr15轴承钢圆棒。

表面粗糙度检测实验现场如图2所示，在外圆磨床进行GCr15轴承钢圆棒磨削加工，四个传感器测试位置按顺序分别布置在头架、床身、尾架、砂轮架四个关键零部件，对磨削加工状态下的外圆磨床产生的振动信号进行加速度数据采集。本次测试总共分四次进行，在工作台不同移速下分别对同一批次的四根轴承钢圆棒进行磨削加工，采集加速度信号数据。并在加工结束之后，采用表面粗糙度测量仪对工件表面粗糙度进行测量。

图2 粗糙度检测实验现场

3.2 粗糙度检测试验测试结果分析

使用上文分形维数提取方法，将测试数据导入编写的振动信号分形维数计算程序中，得到磨削加工过程中工作台不同移动速度下，4根工件圆棒表面粗糙度的测量结果与传感器各个方向的加速度振动波形分形维数的识别结果，如表1所示，表面粗糙度与分形维数之间对应关系曲线如图3所示。

表1 传感器各个方向分形维数

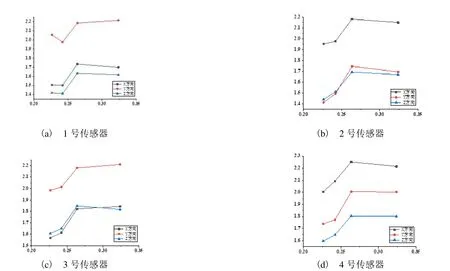
图3 分形维数与粗糙度关系曲线图

结合表1与图3，对分形维数计算结果和表面粗糙测量结果进行分析，可以表明在外圆磨床实际工况中，其他工艺参数不变，工作台在高速时，加工工件表面粗糙度明显低于其余三种运行状态下的测量结果。

分形维数对于低速、中低速与中高速、高速之间的区分度大，在低速与中低速之间、中高速与高速之间区分度都比较小。但是对于工件表面粗糙度的变化趋势能起到一个很好的监测效果；粗糙度低时，分形维数相应大，粗糙度高时，分形维数相应小。多个位置传感器的识别结果具有较好的一致性，因此对测试点的分布位置及数量要求低，操作简单实用性强。

通过分形维数实施监测工件表面粗糙度对振动数据采集位置没有要求，便于实施采用上述方法。通过实时测量外圆磨床加工下的振动数据，实时计算其分形维数，可简单便捷地实时监测磨削加工表面粗糙度，可用于粗糙度在线实时监测。与高速之间区分度都比较小。但是对于工件表面粗糙度的变化趋势能起到一个很好的监测效果。

(4)多个位置传感器的识别结果具有较好的一致性，因此对测试点的分布位置及数量要求低，操作简单实用性强。通过分形维数实施监测工件表面粗糙度对振动数据采集位置没有要求，便于实施采用上述方法。通过实时测量外圆磨床加工下的振动数据，实时计算其分形维数，可简单便捷地实时监测磨削加工表面粗糙度，可用于粗糙度在线实时监测。

4 结语

本文采用盒维数计算方法对处于运行状态下的外圆磨床关键部位进行振动数据信号分形维数提取，提取外圆磨床关键部位的x、y、z三个方向的分形维数，并将其与表面粗糙度测量结果进行了对比分析，成功实现了对工件加工表面粗糙度的监测，同时研究了不同位置的分形维数，发现识别结果具有一致性，证实了该动态测试方案对信号分形维数提取位置要求不高，可操作性高，有利于后续粗糙度在线监测的施行。主要结论如下：(1)分形维数能够快速反应磨削粗糙度的影响、适合大批量的实时在线监测。磨削速度快时，粗糙度越低，分形维数较大，即机床振动较大；磨削速度慢时，粗糙度越小高，分形维数较小，振动较小。(2)在外圆磨床实际工况中，其他工艺参数不变，工作台在高速下，加工工件表面粗糙度明显高于其余三种运行状态下的测量结果。(3)分形维数对于低速、中低速与中高速、高速之间的区分度大，在低速与中低速之间、中速