小净距分离式隧道爆破振动信号降噪方法分析

刘 宇

（中铁投资集团中铁京西（北京）高速公路发展有限公司，北京 102300）

0 引言

爆破是在隧道开挖过程中常用的施工手段。但是在爆破过程中会给周边环境带来影响，因此需要对爆破振动的信号进行提取分析。但是在监测爆破点的工程中，由于存在仪器误差、传递介质反射以及施工环境等因素的影响，因此导致爆破振动信号中存在较多的噪声，为了更准确地分析爆破振动信号的特性，需要对其进行降噪处理。爆破振动信号属于非平稳信号，对这些信号，通常使用经验模态分解（Empirical mode decomposition，EMD），EMD在振动信号降噪方面有很多研究。例如变分模态分解（Variational Mode Decomposition，VMD）通过迭代搜寻变分的最优解，以确定各模态的分量。贾瑞生等人的研究表明，微地震信号噪声大、突变快且随机性大，基于EMD及独立成分分析提出的一种微震信号降噪方法的降噪效果明显。彭亚雄等人针对隧道爆破信号提出基于VMD算法的光滑降噪模型，从而达到去除噪声的目的。综上所述，该文首先利用 EMD、 VMD对爆破振动信号进行分解。其次，利用IMF重构固有模式，构建新的信号以及降噪指标来进行对比分析。最后，对实际隧道爆破振动信号进行降噪处理。

1 降噪原理

1.1 EMD基本原理

EMD是在不需要事先设置基函数的情况下，根据时标特性对信号进行分解的新方法。该方法的核心在于将复杂的信号分解为有限多个IMF，每个IMF成分都含有原始信号在不同的时间尺度上的局部特征。方法步骤如下：1） 在原始信号（）基础上，利用曲线内插法求出信号的最大值、最小值，从而求得信号的上、下包络。2） 求取上、下包络线的平均值，如公式（1）所示。3） 将原始信号（）与平均包络（）相减，以获得剩余的信号（）。通常，对稳定信号来说，这是初始信号的第一个模态函数。但是，对不稳定信号来说，它不会在一定的范围内单调地增加，而是存在1个拐点。如果没有选择这些能够反应原始信号特性的转折点，那么该转折点的精度就会降低，即在一般情况下，该方法的结果并不符合IMF的2个标准，因此必须进一步进行筛选。4） 对剩余的信号（）进行上述处理，最终得到合适的第一阶模态分量（）（即第一个IMF）。5） 对信号 )(和（）进行求差，得出一次剩余值（），用来代替原来的信号，再重复上述操作，就可以获得阶模态函数，最后获得符合标准的剩余值。用 EMD分解得到的原始信号如公式（2）所示。

式中：（）为平均包络线；（）为信号的上包络线；（t）为下包络线。

式中：（）为原始信号；ω（）为第阶模态函数；ρ（）为最终符合标准的残差量。

1.2 VMD基本原理

VMD是一种自适应、完全非递归的模态变分和信号处理算法。该方法在迭代的过程中可以根据实际情况确定各模态的分解数目，从而得到有效的信号分解分量，最终得到最优的变分方案，其分解步骤体现在3个方面：1） 根据实际情况确定所需要的模态分解数目。2） 在后续的迭代解和求解中，使各模式的中心频率与带宽都能自适应地匹配，从而有效地分离 IMF，对信号进行频域划分，进而得到有效的信号分解分量。3） 得到最优化的变分方案。

建立一个变分问题，即将初始信号分成组，保证每个IMF是一个带有有限带宽的中心频率的振型成分，而每个IMF的估计带宽总和是最小的，且约束条件为所有模态的总和与原始信号相等，那么对应的限制变分如公式（3）所示。

在该基础上，引入拉格朗日乘法，把有约束的变分问题转化成无约束的变分问题。采用交替方向乘子（ADMM）迭代算法，将 Parseval/Plancheral、傅里叶等距离变换相结合，对各个模式成分和中心频率进行优化，并在交替寻优迭代后得到μ，ω。

1.3 降噪指标

降噪指标采用线性相关系数表示。相关关系是一种非确定的关系，相关系数是研究变量之间线性相关程度的量，线性相关系数如公式（5）所示。

式中：（，）为线性相关系数；（，）为、的协方差；[]、[]为，的方差。

2 工程应用

2.1 实测信号

某工程为小净距+分离式岩质隧道，隧道穿越的岩石主要为坚硬岩和较软岩，以V级、IV级围岩为主，围岩长度及其占隧道总长度比例见表1。其中，V级围岩主要分布在进出洞口，地层岩性主要为泥岩（多为粉砂质泥岩）以及页岩，属软岩，构造裂隙较发育，层间结合差，围岩自稳能力差，容易产生坍塌。因此，施工时采用三台阶七步法，该方法采用弧形导坑法，以挖出的核心土为基础，分上、下共7个掘进面，采用纵向错开、平行推进的方式进行掘进。

表1 隧道各级围岩分布情况

隧道附近存在多户住宅，为了评估爆破施工对周围环境的影响，采用L-20型振动测试仪进行现场试验。选择了一个具有代表性的爆破振动信号作为实测信号，监测点如图1所示。

图1 监测点位置

2.2 EMD算法

该实测信号的采样频率为10 000 Hz。在对信号进行降噪处理时，选取 0.0 s～1.4 s的信号进行采样。如图2所示（共采集14 334个采样点）。

图2 爆破振动信号

在用EMD方法分解原始信号后，得到的原始信号与本征模态函数分解时域图（图3）。由图3可知，EMD算法可有效地将原始信号分解成多个IMF分量，且每个分量都包括一定的信号特征。

图3 EMD时域图

但是EMD存在的问题之一是端点效应，EMD是利用多个过滤步骤逐一地对IMF进行分解，并利用信号的上、下包络对信号进行局部平均。上、下包络采用样条插补法，得出局部的最大值和最小值。由于信号的两端极大值和极小值是不可能同时存在的，因此上、下包络在数据序列的两端都会产生离散，从而直接影响EMD的质量。

2.3 VMD算法

在利用VMD算法进行分解之前，需要对参数进行设置。保真度取0，惩罚因子取默认值（2 000）。根据中心频率法求模态个数值，见表2。当=8时，最高的中心频率突增，明显产生了过分解现象，因此将值设定为7。分解得到的时域图如图4所示，最后一个分量为低频噪声部分。VMD算法可以很好地将信号分解出来，且

图4 VMD时域图

表2 不同K值下分量的中心频率

能提取一部分低频噪声。

由图5可知，每个IMF分量均具有中心频率，且每个分量有明显的较窄频带，没有明显的模态混叠现象。因此，该算法分解信号是合理的。分析可知，IMF分量可分为3个部分，IMF1～IMF4为第一部分，可以看出爆破过程的初始阶段，IMF5为第二部分，此时爆破产生的影响最大，IMF6～IMF7为第三部分，能量减少，爆破振动带来的影响逐渐消失。

图5 频域图

3 EMD与VMD算法的降噪效果对比

将2种算法所分解的各个分量进行重组，再与原始信号进行对比，从而达到降噪的效果。将IMF1叠加至IMF7，记为信号，将IMF2叠加至IMF7，记为信号，以此类推，直至得到信号。由表3可知，EMD重组信号在信号以后与原始信号相差较多，开始出现失真现象，说明VMD重组信号与原始信号的相关性比EMD更强。在各个重组信号中，与EMD方法相比，VMD方法具有更好的性能（ EMD算法具有二进制滤波特性），虽然它是自适应的，但是在信号、噪声以及脉冲等复杂环境下，它的包络运算受到了一定的影响，进而影响模态分解，出现混叠的现象，让IMF成分丧失了物理含义。而 VMD则是一套维纳滤波算法，对噪声有较强的鲁棒性，利用该方法使模态和中心频率不断调整、更新，从而获得更好的信号分解效果。这充分证明了VMD算法比EMD算法更具优势。

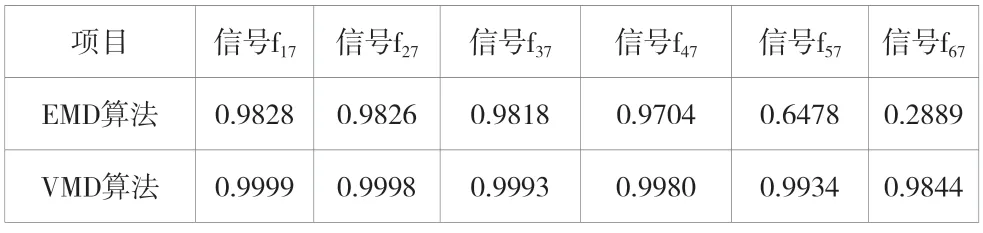
表3 降噪指标

4 结语

综上所述，该文得出2个结论：1） 针对实测隧道爆破振动信号的特征部分被大量噪声掩藏的技术难题，对爆破振动信号分布进行EMD和VMD分解，得到多个不同频率的IMF分量。由VMD分解得到的IMF比EMD算法更好，同时还能很好地剔除低频噪声。2） 对不同算法得到的IMF分量进行重组，通过降噪指标的大小来判断重组信号与原始信号之间的相关性，并判定重组信号的降噪效果。结果表明，VMD算法比EMD好，能得到更好的降噪效果。