组合动力飞行器动力转换过程推阻匹配与控制
刘得冕 陈永亮 吴 杰
(南京航空航天大学航空学院,非定常空气动力学与流动控制工业和信息化部重点实验室 江苏 南京 210016)
0 引言
目前,越来越多学者对组合动力飞行器动力转换过程中的推阻平衡和姿态控制进行研究。美国国家航空航天局(National Aeronautics and Space Administration,NASA)在已建立的TBCC发动机数学模型的基础上研究了模式转换过程中的推力稳定问题,提出了一种LQR增益设计方法来控制飞行器,从而使推力损失最小。目前,国内很多高校对TBCC发动机内部部件进行优化,降低了发动机在动力转换过程中的推力损失。
由于上述方法未考虑飞行器在动力转换过程中发动机进气道干扰对飞行器气动参数的影响。而在对发动机本体进行优化时,也未考虑飞行器在进行动力转换时飞行器姿态的变化对发动机的影响。因此,笔者针对上述方法存在的问题进行了分析、改进、仿真及蒙特卡洛测试,具体内容如下。
1 组合动力飞行器建模
该文研究的组合动力飞行器模型是根据NASA公开的飞行器模型,该模型六自由度方程可以由如公式(1)、公式(2)所示的非线性方程组来描述。




式中:、以及分别为飞行器的参考面积、飞行器所处高度的大气密度和基准长度;C、C以及C分别为升力系数、阻力系数以及侧力系数;C、C以及C分别为无量纲化后的滚转力矩系数、俯仰力矩系数以及偏航力矩系数;、为涡喷发动机和冲压发动机的输出推力;、以及分别为飞行器所受到的阻力、侧力和升力;为发动机输出推力;为飞行器速度 ;为飞行器展长;为飞行器弦长。
2 模态转换参数调节过程
通过改变分流阀随时间的变化规律使分流阀随时间非线性地变化,整个仿真时间为65 s,动力转换过程为60 s,变化如公式(3)所示。

式中:()为时间;、分别为冲压发动机和涡喷发动机的分流阀开度;为时间;、以及分别为涡轮发动机输出推力、冲压发动机输出推力和发动机输出总推力。
由图1可知,当组合动力进行模态转换时,发动机的输出推力不是一个常值。当组合动力发动机进行动力转换时,涡喷发动机将流量分给冲压发动机,此时涡喷发动机输出推力减弱,冲压发动机输出推力缓慢增加。这时为了增强涡喷发动机的输出推力,笔者加大了涡喷的油门开度,随后涡喷发动机的输出推力逐渐增强。但是随着流量阀的逐渐打开,也会导致涡喷发动机燃烧不充分,其输出推力变小,这时冲压发动机的输出推力在不断增大,为了减少燃料的浪费应逐渐调小涡喷的油门开度,在转换完成后,发动机的输出推力为冲压发动机的最大推力。在姿态稳定的情况下,组合动力飞行器在动力转换过程中的高度和速度的变化如图2、图3所示。

图1 模态转换推力随时间而变化的情况
由图2、图3可知,在动力转换过程中,组合动力飞行器高度的最大损失为450 m,速度的最大损失为5 m/s。考虑打开分流阀会对飞行器本体的气动参数产生摄动,因此需要对控制器设计的鲁棒性提出要求。

图2 模态转换高度随时间而变化的情况

图3 模态转换速度随时间而变化的情况
3 模态转换段控制律设计
3.1 俯仰角LQR控制器设计



可将公式(4)简写为公式(5)。

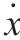
模型的输入量如公式(6)所示。

式中:为系统的状态变量;为需要LQR设计的反馈系数矩阵(由MATLAB计算得出);为前馈增益。
在 公式(6)中,M=k,=q,K=[k,k,k,k,k](k,k,k,k和k分别为轴速度、轴速度、俯仰角速率、俯仰角和误差通道的反馈增益)。将输入量的表达式带入原状态空间方程,重构成新的状态空间方程,如公式(7)所示。

3.2 俯仰角动态逆控制器设计
俯仰角控制以俯仰角速率控制作为内回路,采用动态逆的方法设计控制律。根据飞行器纵向运动学方程(公式(1))可以转换为俯仰角的动力学方程,如公式(8)所示。


为了确保俯仰角能够快速跟踪指令,迎角控制采用比例控制的结构,迎角变化率如公式(9)所示。

式中:k为迎角控制回路的带宽;θ为俯仰角速率指令。
将公式(9)代入公式(8),结果如公式(10)所示。

通过公式(10)求俯仰角回路的控制律,如公式(11)所示。

式中:q为俯仰角动态逆控制律生成的俯仰角速率指令。
俯仰角动态逆控制回路的带宽选择应为俯仰角速率回路带宽的3~5倍,设计k为1.6 rad/s。
3.3 俯仰角速率环L1自适应控制器设计
自适应控制律是同时满足快速性和鲁棒性要求的自适应控制算法。控制器的设计主要由3个部分组成,分别为状态观测器、自适应律以及控制器(包括控制器和低通滤波器)。由公式(1)可以得到组合动力飞行器俯仰运动的动力学方程,如公式(12)所示。

俯仰力矩如公式(13)所示。


由于面对称飞行器的交叉转动惯量I较小,因此可以忽略其影响,组合动力飞行器的俯仰动力学方程如公式(14)所示。

由于动力学模型中存在不确定性的情况,因此可将公式(14)改写为公式(15)。


公式进一步表示为公式(16)。
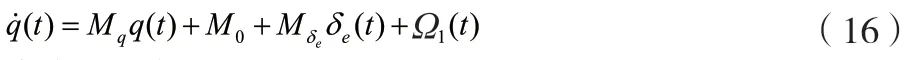
将模型重构,如公式(17)所示。




对比公式(17)、公式(18)可知,ωq=ωMδ,=(ω+M),=Mα+。
状态观测器的形式如公式(19)所示。

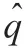
自适应律如公式(20)所示。


控制律如公式(21)所示。

式中:K为前馈增益;K为自适应反馈增益;为低通滤波器。
3.4 俯仰角速率环自抗扰控制器设计
自抗扰控制器是较为理想的解决组合动力飞行器强耦合性、强非线、干扰性和不确定性的控制方法。其设计思路及算法主要包括3个部分。
二阶微分跟踪器如公式(22)所示。

式中:为最优控制输出值;为输入参考指令;和分别为参考指令的滤波信号和一阶微分信号;为速度因子;为滤波因子;是最速控制综合函数。
扩张状态观测器是自抗扰控制器设计中最核心的一环,它将所有与积分串联型系统不匹配的地方当作一个新的状态,根据系统的输入、输出信息对其进行观测和估计,具体的算法如公式(23)所示。

式中:、以及分别为系统的状态变量、状态变量的微分值和由ESO得出的扰动总和的估计值;、和为ESO需要的设计的参数,可以参考斐波拉契数列;和分别为系统的控制输入量和系统的实际输出量;为线性区间长度,且0<<1;(,,)为用以估计的非线性函数。
(,,)的具体定义如公式(24)所示。

式中:为指令跟踪误差;为跟踪因子。
在自抗扰控制器的设计过程中,非线性误差反馈控制律是对由TD和ESO得到的状态误差反馈进行非线性或者线性组合,再减去扩张状态观测器对系统干扰的估计值,实现在线补偿,从而得到相应的控制量,具体定义如公式(25)所示。

4 仿真计算与分析
组合动力飞行器整个动力转换过程仿真的初始状态是涡喷发动机单独工作时的配平状态,飞行速度为3 Ma,飞行高度为20 km。整个仿真过程为80 s,前60 s为发动机动力模态转换(即由涡喷发动机转换为冲压发动机的模态转换过程),后20 s为纯冲压发动机工作。
由图4可知,在仿真过程中,如果不对俯仰角施加控制,那么飞行器本体是不稳定的,因此需要引入控制器进行增稳。

图4 开环情况下俯仰角的响应特性
由图5可知,采用线性模型的LQR控制器和采用非线性模型的动态逆-鲁棒自适应控制器均能很好地跟踪1.5°俯仰角指令。但相比之下,采用动态逆-鲁棒自适应控制能够更快并且超调量更小地跟踪俯仰角指令。此外,LQR控制器是针对线化后的线性模型所设计的,当将它用在非线性模型上时,其对俯仰角指令的跟踪过程如图6所示。

图5 闭环控制下俯仰角的响应特性
由图6可知,组合动力飞行器在前50 s时,LQR控制器能够较好地跟踪俯仰角指令。但是在50 s过后,系统逐渐发散,导致飞行器无法进行动力转换,因此在接下来的动力转换过程中采用动态逆-鲁棒自适应和动态逆-自抗扰的控制方法。

图6 非线性模型下LQR控制下俯仰角的响应特性
由图7可知,采用动态逆-自抗扰以及动态逆-鲁棒自适应控制均能够很好地跟踪俯仰角指令。

图7 俯仰角随时间而变化的情况
由图8可知,当上述的控制律跟踪给出的俯仰角指令时,还留有一定的舵偏余量,具有较好的鲁棒性。

图8 升降舵偏量
由图9可知,组合动力飞行器本体航向通道是不稳定的,此时飞行器几乎没有抗侧风能力,需要引入相应的控制器。

图9 开环情况下侧滑角的变化量
为了测试控制系统的抗侧风能力,在仿真过程中加入速度为100 m/s的侧风,其侧滑角和方向舵舵偏角的响应过程如图10、图11所示。
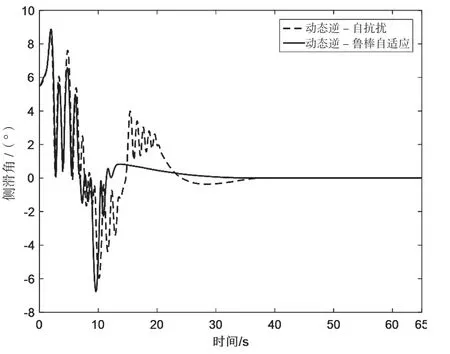
图10 侧滑角随时间而变化的情况
由图10可知,与采用动态逆加上内环自抗扰的控制方法相比,采用动态逆加上鲁棒自适应控制的方法使飞行器在进行模态转换且受到侧风干扰时,能够更快地恢复到原有的平衡状态。
由图11可知,以自抗扰和鲁棒自适应控制做为内环增稳都具有较强的抗侧风能力,当模态转换开始时因分流阀对周围空气干扰而导致侧滑角的响应变化过程有些剧烈,大约在30 s时,侧滑角稳定在初始配平状态0 °(有浮动),此时的方向舵还有一定的余量,具有一定的鲁棒性。

图11 方向舵随着时间而变化的情况
在组合动力飞行器进行动力转换的过程中,发动机的分流阀会逐渐将涡喷发动机的流量过渡到冲压发动机,对飞行器的气动参数产生影响。因此需要采用蒙特卡洛方法验证俯仰角控制律的鲁棒性,各参数拉偏范围见表1。

表1 滚转角控制律蒙特卡洛仿真的各项参数拉偏范围
由图12蒙特卡洛测试俯仰角的响应曲线可知,当采用动态逆加上鲁棒自适应控制对飞行器各项参数进行拉偏时,仍然可以较好地跟踪俯仰角指令。
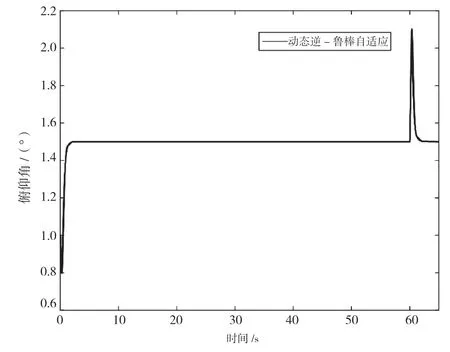
图12 蒙特卡洛测试俯仰角的响应曲线
由图13蒙特卡洛测试下升降舵偏量可知,当控制器进行指令跟踪时,即使发动机在进行模态转换,升降舵仍然还有一定的剩余量,具有一定的鲁棒性能。
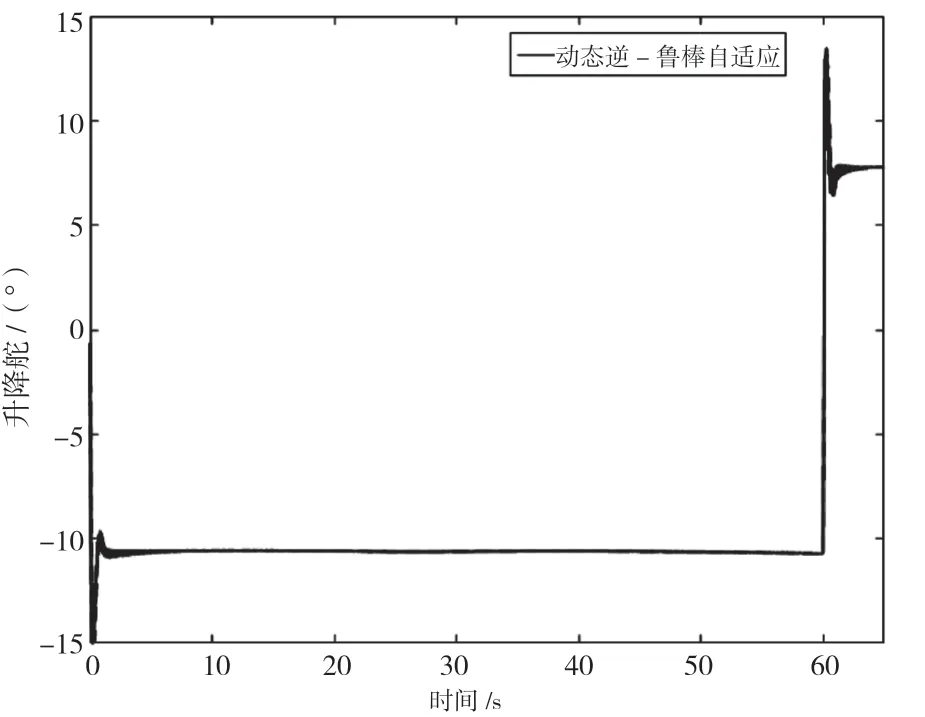
图13 蒙特卡洛测试下升降舵偏量
由图14蒙特卡洛测试俯仰角的响应曲线可知,当发动机完成动力转换(60 s)时,由于气动参数的变化会对俯仰角产生较大的干扰,因此采用动态逆加自抗扰的控制方法能够很好地消除干扰,从而更好地跟踪原有的俯仰角指令。

图14 蒙特卡洛测试俯仰角的响应曲线
由图15可知,以自抗扰和鲁棒自适应作为内环增稳均可保证组合动力飞行器能够顺利实现动力转换,俯仰角响应能够在一定的参数摄动范围内跟踪指令,升降舵的舵偏也未饱和,俯仰角控制律鲁棒性较好,满足控制设计要求。相比之下,当使用自抗扰控制时,飞行器俯仰角的超调量较小。此外,2种控制器的设计均有一定的抗侧风能力。从控制律设计来说,鲁棒自适应控制律是基于模型设计的,因此关于鲁棒自适应的调参相对有规律可行,但是控制律的设计需要对飞行器本体的动力学特性有较为深刻的理解。自抗扰控制律的设计是基于非模型设计的,因此具有更好的适用性,但是参数的调整需要花费一定的时间并且参数的选定对控制的效果影响较大。

图15 蒙特卡洛测试下升降舵偏量
5 结语
首先,该文针对组合动力飞行器在动力转换过程中存在推力损失,飞行器本体气动参数存在较大的摄动和不易控制的问题,提出了在动力转换过程中分流阀和油门随着时间的关系,使组合动力飞行器在动力转换过程中速度降低了5 m/s,高度损失了450 m。在该基础上采用基于纵向通道线性模型LQR控制发现,在非线性模型中使用LQR控制器时会发散。其次,该文提出了基于外环动态逆和内环鲁棒自适应控制或ADRC的控制方法。该方法具有控制精度高、鲁棒性强的特点。通过数值仿真验证了该文设计的控制器能够解决飞行器在模态转换过程中的状态控制问题,且具有一定的抗侧风能力。最后,该文还采用蒙特卡洛测试的方法对组合动力飞行器气动参数、推力以及质量惯性进行参数摄动。由仿真结果可知,设计的控制器具有一定的鲁棒性能,更符合实际飞行器的工作状况。

