定热流边界下重力作用PCM熔化过程规律

张春伟，李山峰，郭永朝，张学军，江龙

（1 北京航天试验技术研究所，北京 100074；2 浙江大学制冷与低温研究所，浙江杭州 310027；3 浙江省制冷与低温技术重点实验室，浙江杭州 310027）

相变材料（phase change material, PCM）是相变储热技术应用的基础，可大规模推广的相变材料应具有价格便宜、储能密度大、无毒、腐蚀性小、化学性能稳定等特征。然而，绝大多数相变材料的导热性较差，需要采用相应的传热强化方法。对于任一传热过程，主要有三个参数影响传热速率，即热导率、换热面积和温差，所以主流的传热强化方法可以归纳为以下三种：强化PCM 热导率、拓展换热表面和提升热传递过程的总体温差，具体包括应用热管、翅片、泡沫铜、高导热添加剂、多级串联等方式。除此之外，相变储热器的安装倾角也会显著改变封闭方腔内流体的努塞特数，进而影响PCM的熔化速率。近年来，关于倾角影响已有一些初步研究。

Sharifi 等（竖直基准）研究了PCM 在圆柱壳体中的熔化行为，加热棒与圆柱壳体同心放置。实验结果表明，储热单元倾斜会影响PCM 的温度和固液分布演化过程。Baby 和Balaji（未知基准）通过实验评估了倾角对填充PCM 的泡沫铜热沉传热能力的影响。在熔化时间为160min 时（0°、90°和180°），热沉底部温度分别为49.92℃、50.42℃和51.19℃，所以当热沉的倾角为0°时，传热性能最好。Groulx 和Biwole（竖直基准）模拟分析了用于光伏板温控的方腔PCM 熔化过程，倾角变化范围是0°～90°。结果表明，当倾角从0°到60°时，PCM 的熔化以对流换热为主，装置热特性及储能速率相差不大；而当倾角为90°时，方腔内PCM出现明显的热分层现象，传热机制基本为热传导。Kamkari 等（水平基准）通过实验研究了矩形方腔内PCM 在不同倾角下熔化的动态热特性。实验结果表明，方腔倾角对自然对流的形成有显著影响，当倾斜角度从90°减小到0°时，方腔内的对流增强。倾角为0°和45°方腔的PCM总熔化时间分别比90°倾角少53%和35%。Seddegh等比较了石蜡在水平和垂直放置的壳管式相变储热单元中的熔化特性。当PCM 的上半部分熔化时，水平放置单元的传热更有效，而当下半部分PCM 熔化时，水平放置的熔化速率则相对较差，但在整个储热过程中，水平放置时的效果好于竖直放置。Pahamli等（水平基准）对管壳式换热器内相变材料的熔化进行了实验数值研究，分析纳米颗粒和倾角对材料性能的影响。研究结果表明，倾角越大，熔化速度越快，熔化总时间越短，即竖直放置时性能最优。Al Siyabi 等（竖直基准）通过模拟和实验研究了倾角对壳管式相变储热系统性能的影响，结果表明，当倾角为45°时，PCM 的熔化速度比0°和90°倾角快，PCM 的熔化时间比0°倾角的熔化时间缩短了13%。当倾角为90°时，储热器下部的PCM很难完全熔化。Mehta 等（未知基准）通过实验对比了水平和垂直方向的管壳式相变储热单元的性能。在设定工况下，水平放置时的PCM 熔化一半所需时间比竖直放置时少了25%；而在凝固过程，两个结构未观察到明显差异。Kalapala 等（竖直基准）研究了处于0°、30°、60°和90°倾角下的管壳式相变潜热单元的性能。倾角对熔化过程有重要影响，而对凝固过程的影响则可忽略。储热单元水平放置时，上半部分PCM 的熔化速率较快，而竖直放置时的总熔化时间较短。

虽然倾角对于PCM 的熔化有重要影响，但现有研究只简单测试特定角度下的PCM 熔化特性，如0°、45°和90°等。同时，由于倾角的定义和相变储热单元结构不同，研究结果不具备可对比性，所得结论也往往冲突或矛盾。鉴于此，本文基于倾角影响PCM 熔化过程的本质因素，建立一套通用分析坐标，使所有研究倾角影响的结果可统一比较；选择经典方腔作为研究对象，建立可视化实验台及数值计算模型，分析不同倾角下熔化时间、自然对流强化效果、液化率特性、固液及温度分布演化过程及特性，获得典型热流边界下的倾角作用PCM熔化过程规律。

1 重力作用过程分析

倾角影响PCM 熔化过程的本质为重力对熔化过程的附加作用，具体为热流方向与重力方向夹角的影响。由于重力为恒定不变的常量，可以据此来定义热流方向与重力的通用坐标，随后搭建固液界面演化实验台并建立相应数学模型，研究多种工况下重力对PCM熔化过程的作用规律。

1.1 通用坐标

相变储热器角度分布对熔化过程的作用本质为重力和浮升力综合影响下的PCM 熔化过程自然对流演化规律。定义的通用坐标如图1所示，以重力方向为基准，调整热量输入方向，进而改变夹角的大小。当热量输入方向与重力方向相同时，两者的夹角为0°或360°；当热量输入方向与重力方向相反时，两者的夹角为180°。由于对称性，后续只分析0°～180°即可。

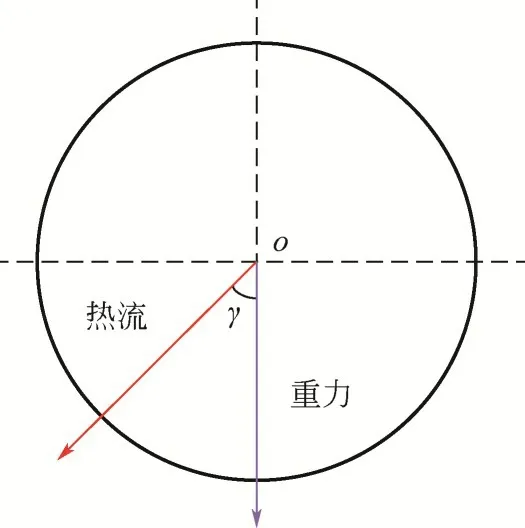
图1 通用坐标示意图

1.2 物理模型及测试装置

方腔物理模型如图2所示。为便于理解重力作用的变化，采用倾角调控夹角的大小，两者的转化关系为=+180°。

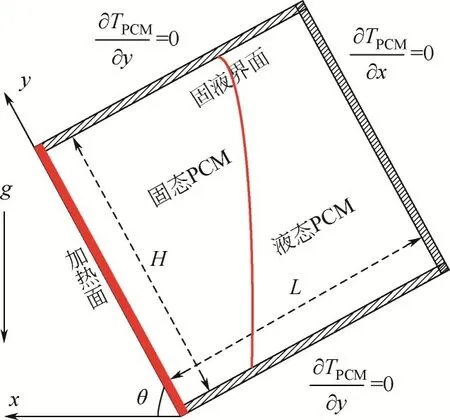
图2 方腔在倾角θ下的物理模型示意图

搭建的定热流边界方腔可视化实验装置如图3所示，腔体采用双层结构设计，内部为透明橡胶板[0.16W/(m·K)]，外部为亚克力板[0.18W/(m·K)]。方腔壳体由硬木构成[0.15W/(m·K)]，双层结构与木质壳体通过通孔螺丝连接。采用电加热棒模拟定热流边界，电加热棒外接可调直流电源。方腔实际长、宽分别为60mm、50mm，由于电热棒的外径为10mm，所以可供观察的方腔面积为50mm×50mm。

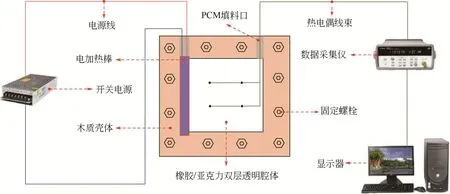
图3 定热流边界可视化方腔实验装置原理

为减少熔化过程中热量损失，PCM 的熔化温度应尽可能趋近于环境温度。因此，经过多方面因素的综合考量，PCM 选用十四醇，相变温度约为37.8℃，DSC 测试结果如图4 所示。热导率约为0.16W/(m·K)，热膨胀系数为1.018×10，详细参数可见文献[18]。十四醇首先在烘箱内进行加热液化，随后通过方腔的填料口灌注到方腔中。由于十四醇属于有机类相变材料，所以固液相对应的体积存在差异。灌注完成后，方腔外部贴保温材料，并通过支架固定。方腔内PCM 的初始温度通过室内空调控制，虽然空调调控的温度并不恒定，但经过保温材料与腔体结构对温度波动的弱化，内部PCM温度可以近似维持在设定值。

图4 十四醇DSC测量曲线

2 数值模型建立及验证

2.1 数学控制方程

在数值模型中，采用等效比热容法模拟PCM的熔化和凝固过程，根据Boussinesq近似模拟液态PCM 的自然对流，同时假设液态PCM 的流动为不可压缩层流且壁面为无滑移边界条件。基于上述假设条件，可列出连续性方程、动量方程和能量方程如式(1)～式(4)。

连续性方程

方向的动量方程

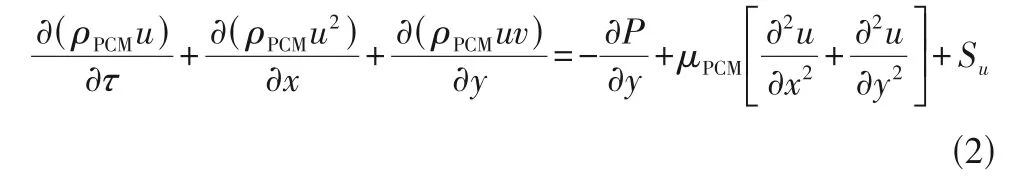
方向的动量方程

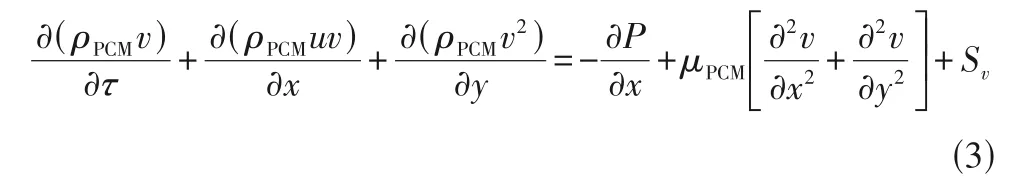
相变材料能量方程

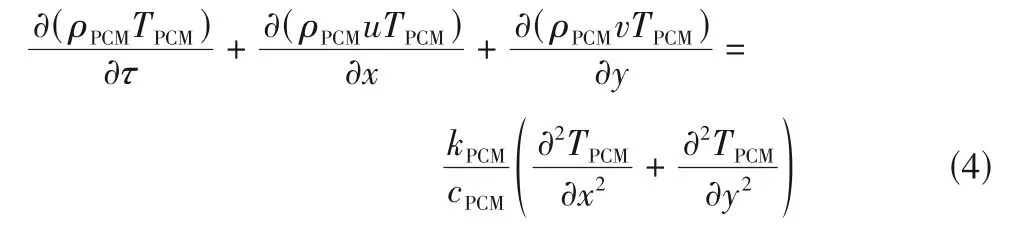
上述公式中的源项为式(5)、式(6)。

为实现数值计算稳定性，假设PCM 的熔化和凝固过程发生在一个设定温度区间（～)内。对于方腔模型，左侧边界为定热流边界，另外三条边界为绝热，如式(8)～式(11)所示。采用附加源项法处理边界条件，即把进入或流出计算区域的热量作为与边界相邻的控制容积的当量源项，此处不再详细展开。

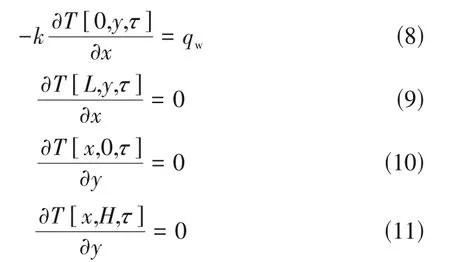
2.2 模型有效性验证

在进一步分析前，需要对模型有效性进行测试。控制方程采用全隐式格式处理时间项，相应的代数公式通过结合超松弛技术的高斯赛德尔迭代法数值求解，采用结合同位网格压力关联方程的半隐式方法（SIMPLE）求解压力修正方程，上述过程通过MATLAB 软件实现。对于连续性、动量和能量方程的收敛标准分别为10、10和10。在网格无关性方面，为了在求解精度和计算时间之间取得平衡，最终选取网格数12000 和时间步长0.02s。在模型准确性验证方面，虽然搭建了方腔可视化实验装置，但由于PCM 的导热性低，在长时间熔化过程中界面漏热不可避免，导致实验的固液界面演化明显滞后数值模拟结果。所以选取方腔数值研究的通用实验对模型进行验证。在该实验中，将低温金属镓选为PCM，热导率为29.4W/(m·K)，明显大于方腔壳体的热导率，可弱化漏热对PCM 熔化过程的影响。模拟结果与文献[22]的通用实验对比情况如图5所示，其中，镓的物性参数可通过文献[23]获得。

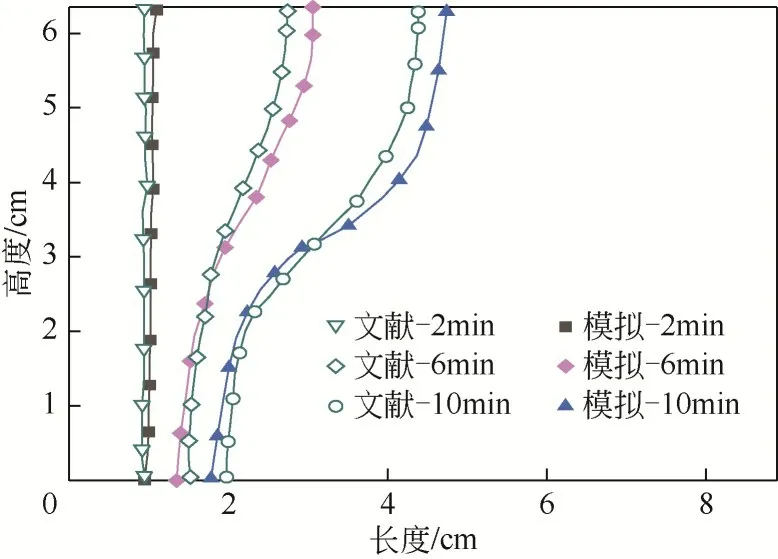
图5 数值模型结果与文献的结果对比

3 结果分析与讨论

由于实验控制难度较大，可视化实验仅在倾角为0°、60°和90°时（对应效果分别与夹角为180°、120°、90°时相同）分析方腔内部的固液界面演化过程。作为补充，数值模拟则系统地分析了夹角对熔化过程的影响，每隔15°进行一次计算，选取夹角的数值为0°、15°、30°、···、150°、165°、180°。

3.1 可视化实验

图6 为定热流边界下的0°、60°和90°倾角的PCM固液分布演化过程。当倾角为0°时，固液界面首先近似平行于电加热棒，随后在自然对流和腔体边界漏热的双重影响下，固液界面呈现出中间高、两侧低的分布情况。当倾角为90°时，液态PCM 沿加热棒上升，并逐渐聚集于腔体上部。随着熔化过程的进行，方腔上半部分的液态区不断扩大，呈现“上宽下窄”的分布情况，固液界面也逐渐向下方推进，但由于温差的限制，后半部分固态PCM 所需的熔化时间会更长，在熔化后期，腔体底侧还存在未熔化的PCM薄层。当倾角为60°时，高温液态PCM 竖直上升，与固态PCM 的接触面相对于90°倾角更大，相应的传热能力也会增强。此外，由于有机类PCM 固液密度差导致体积不同，所以在右上角存在少量固态PCM。

图6 定热流边界下的不同倾角θ下的固液界面演化

3.2 熔化时间对比

图7为定热流边界下不同夹角对应的熔化时间，其中图7(a)、(c)和(d)为不同方腔尺寸下的熔化性能对比，图7(b)、(c)和(e)为不同定热流边界下的熔化性能对比。对于图7(c)，夹角为0°时，PCM熔化过程为纯导热，对应的熔化时间为37.87min；夹角为15°时，对应的熔化时间最长，为53.14min，相对纯导热过程增加了40.32%；夹角为120°时，对应的熔化时间最短，为13.97min，相对纯导热过程减少了63.11%。对图7 整体对比可知，在排除夹角为0°时，其余的PCM 熔化时间均先减小后增大，即均存在最优夹角值，使腔体中的PCM 熔化时间最小，最优夹角均大于90°且小于180°。此外，随着腔体长宽比（/）的减小，PCM 熔化时间明显减小；而随着热流增加，PCM熔化时间也明显减小，同时不同夹角对应熔化时间的差值也逐渐增大。

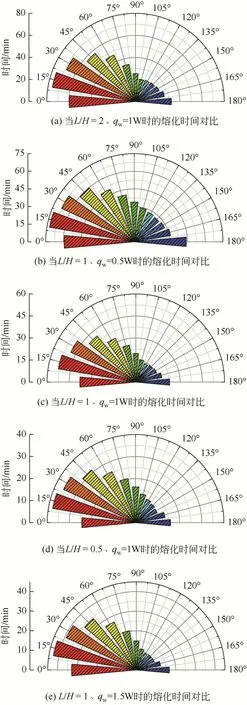
图7 定热流边界不同夹角γ对应的熔化时间

3.3 自然对流强化效果对比

与纯导热工况下的0°夹角熔化时间进行对比，分析自然对流对熔化的作用。定义自然对流强化百分数作为对比参数，即=(-)/，式中为待分析夹角熔化时间；为0°夹角熔化时间。图8 为定热流边界下的夹角对应的自然对流强化效果。由其可知，夹角较小时，自然对流对PCM 的整体熔化过程有抑制作用，而只有在夹角大于一定数值时，自然对流才能促进PCM 的熔化过程。随着腔体长宽比的减小，自然对流对整体熔化时间的抑制作用范围增大，而在较大夹角的促进作用也逐渐下降；随着热流增加，自然对流对整体熔化时间的抑制作用变化不大，但在较大夹角的促进作用也明显提升。

图8 定热流边界不同夹角γ对应的自然对流强化百分数对比

3.4 特定夹角液化率演化

分析特定夹角下PCM 熔化过程的液化率曲线与温度云图演化过程，有助于了解夹角对熔化的作用机理。选取的夹角为0°、45°、90°、135°和180°。图9 为定热流边界特定夹角对应的液化率演化过程。0°夹角下PCM 的熔化过程为纯导热过程；45°夹角对应的液化率曲线在熔化前期明显快于纯导热过程，但在熔化后期，液化率曲线增长速率下降，具体原因可通过后续的温度分布云图演化得知；90°夹角对应的液化率曲线与45°夹角类似，在液化率约为0.9之前，PCM 液化速率较快，但剩余部分的液化速率明显降低；与90°夹角相比，135°夹角的液化率曲线近似匀速上升，两者熔化最后阶段的上升速度不一，进而造成对应熔化时间的差异；180°夹角的液化率曲线也以近似线性特征上升，但总熔化时间明显小于纯导热工况的0°夹角。此外，随着腔体长宽比减小，除整体熔化时间减小外，45°和90°夹角在熔化后期的液化曲线变化相对更加平缓。所以除改变夹角外，增加壁温或改变腔体长宽比也可加速PCM熔化。

图9 定热流边界特定夹角γ对应的液化率演化过程

3.5 固液和温度分布演化

为明晰前述特定夹角对应的液化率曲线变化原因，选取图9(c)的工况下每一个夹角的典型固液分布云图和温度云图进行分析，液化率分别为0.2、0.5和0.8。图10～图14为相应的云图演化过程。对于0°夹角，由于以纯导热进行传热，所以固液界面与加热面平行。温度梯度在液态PCM 区域内较为明显，在固态PCM 区域内不明显，这是由于PCM 初始温度与相变温度间的差值小于热源与相变温度间的差值。同时，由于方腔后期热量输入较多，所以固液界面的宽度变化幅度也相对较小。

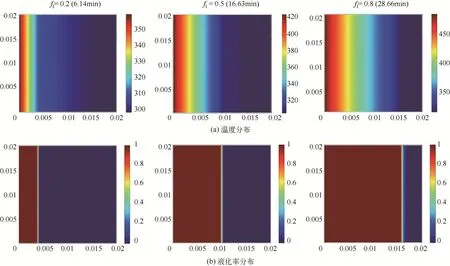
图10 定热流边界0°角方腔熔化过程的温度分布和液化率分布

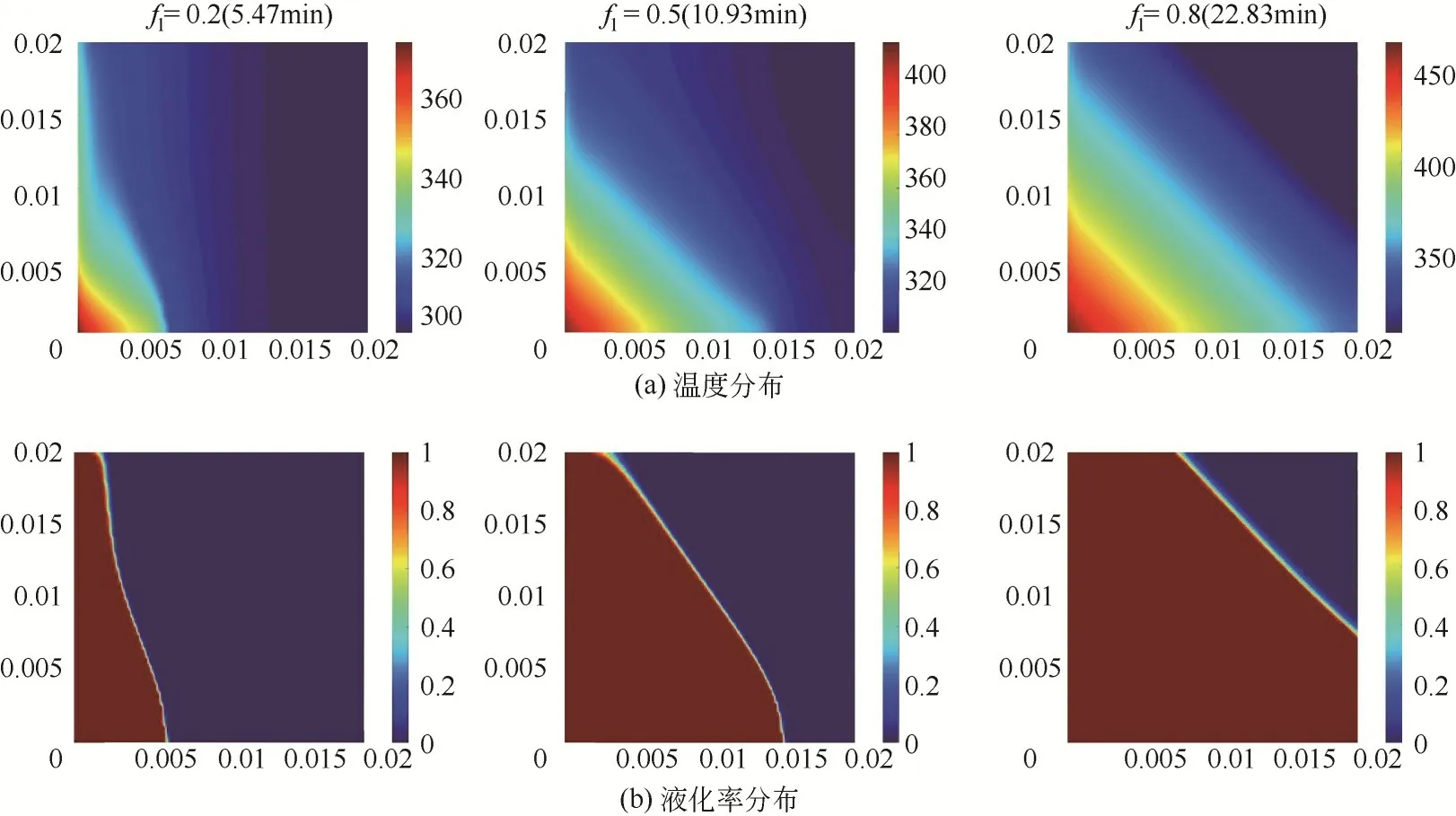
图11 定热流边界45°角方腔熔化过程的温度分布和液化率分布

图12 定热流边界90°角方腔熔化过程的温度分布和液化率分布

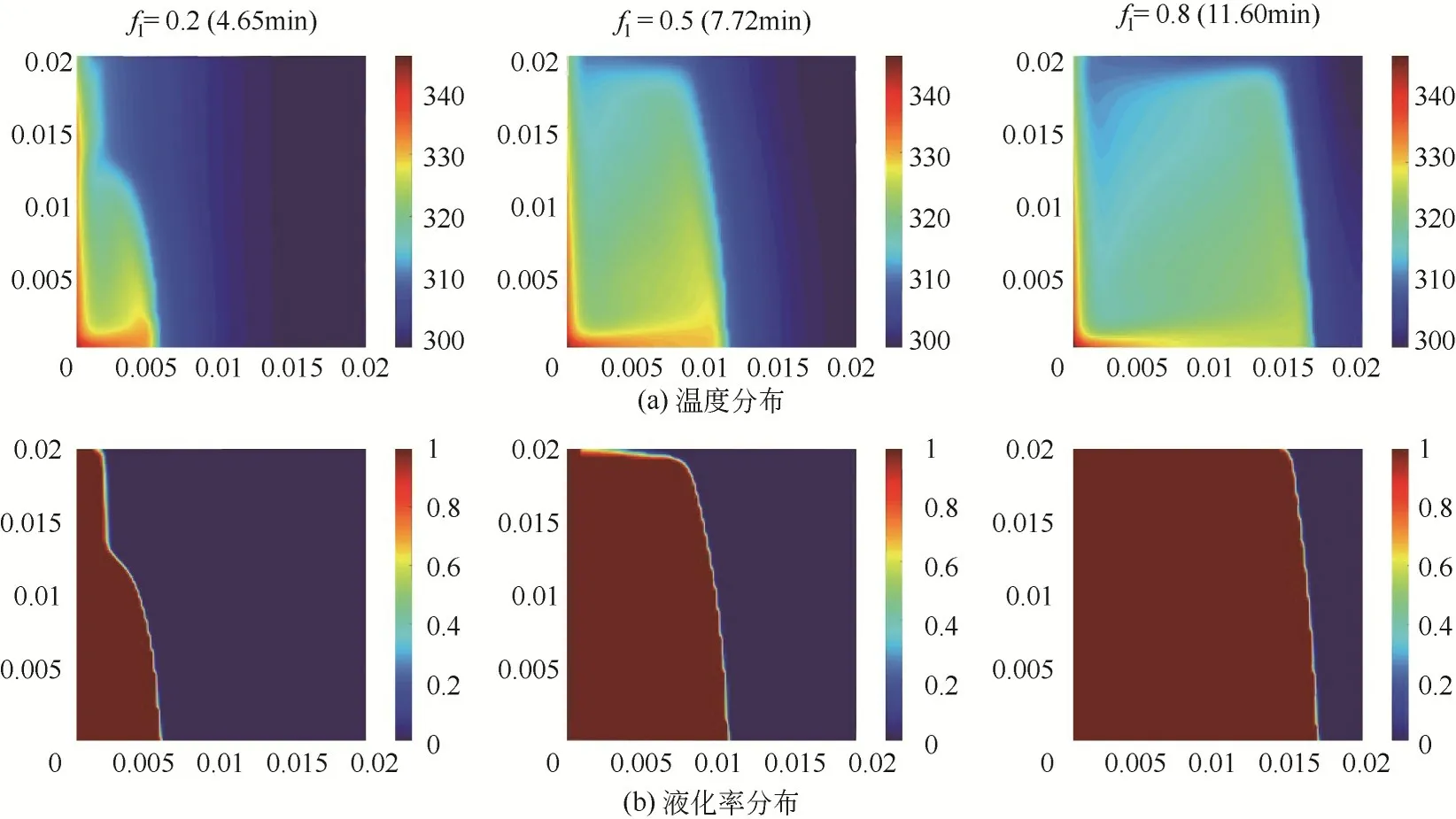
图13 定热流边界135°角方腔熔化过程的温度分布和液化率分布

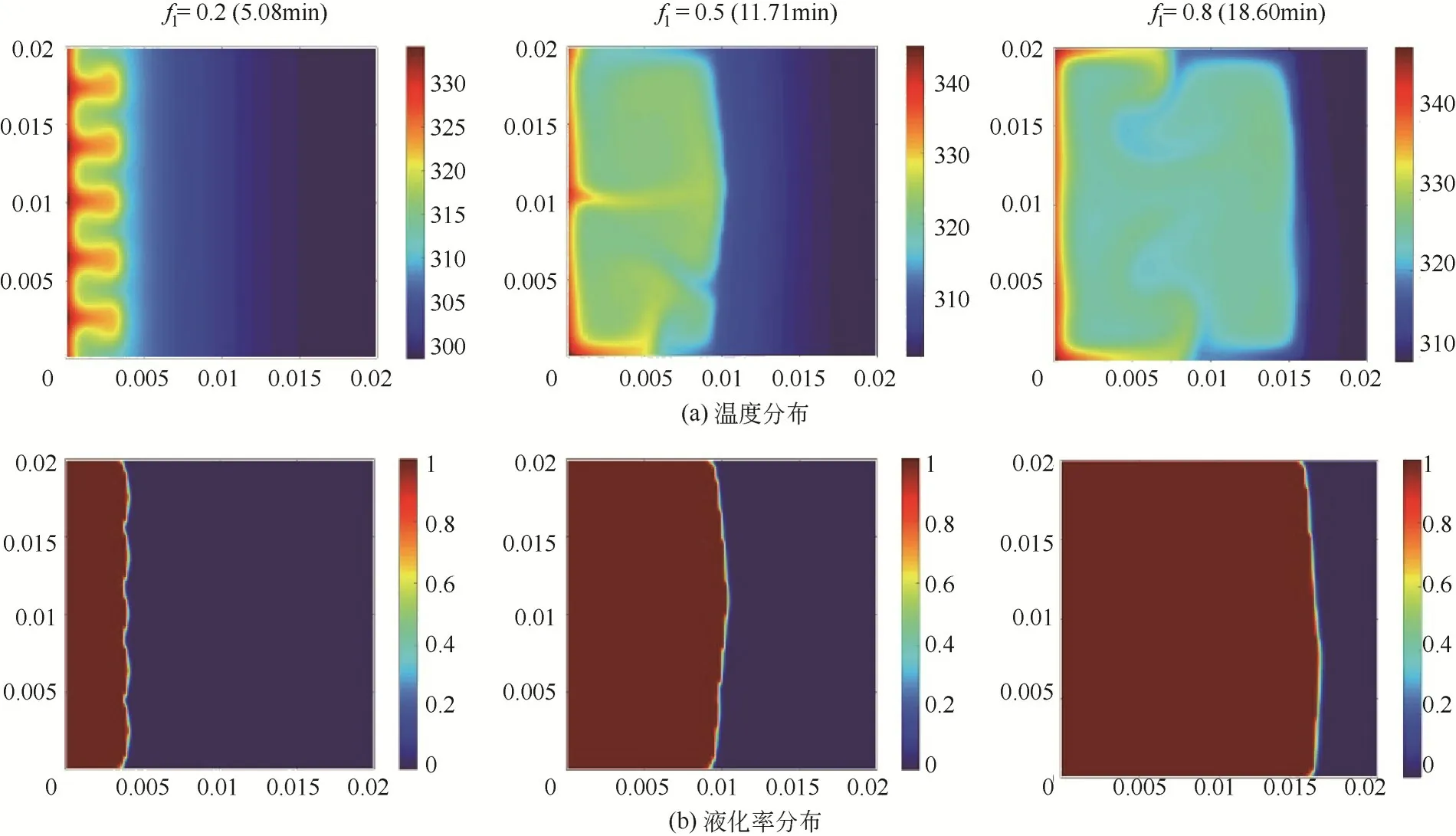
图14 定热流边界180°角方腔熔化过程的温度分布和液化率分布

对于45°夹角，熔化的高温液态PCM 逐渐向上，并聚集到方腔边角，由于腔体结构的限制，高温液态PCM 承载的热量较难继续向下传递，主要依靠回流的低温液态PCM 完成换热；随着固液界面继续向下延伸，当低于加热面下部时，下半部分固体PCM只能以纯导热完成液化。

对于90°夹角，高温液态PCM 首先沿加热面上升，随后沿上壁面前行，最终到达固液两相区，途中不断释放热量，完成热量自加热面高固液界面的快速传递。但到熔化过程后期，受腔体结构及驱动力影响，自然对流的作用空间不再快速增加，所以左下角区域的固态PCM 熔化速率较慢，延长了方腔内PCM 的整体熔化时间。对于135°夹角，由于方腔倾斜，高温液态PCM 的流动距离相对更远。同时固液界面在方腔高度上的分布也相对90°夹角更加均匀，所以其液化率曲线也以近似线性增长。

对于180°夹角，源自壁面的高温液态PCM 直接向上流动，并在黏性力等作用下，形成了一些较小的局部回流区，随着液态PCM 的不断增加，小的回流区不断合并成较大的回流区。固液分布界面呈现中间高、两侧低的特征，符合可视化实验装置观测的结果。当液化率达到0.8 时，由于作用空间增大且液态PCM 温度梯度减小，自然对流区域变得更加复杂，沿两侧边界上升的高温液态PCM 与回流的低温液态PCM 碰撞，进而形成了两个小的回流区，所以换热效果相对弱于90°和135°夹角对应的自然对流。但在整体过程中，自然对流都在不断加速热量自加热面到固液界面的传递，所以该夹角下的液化率曲线可以近似线性地上升。此外，由于定热流的热量输入特性，高温液态PCM 与低温液态PCM 碰撞导致的流动分布更加复杂。

4 结论

为探究定热流边界下的重力作用PCM 熔化过程的规律，以重力方向为基准，定义通用分析坐标，搭建可视化方腔实验台以及建立数学模型，分析多工况下的PCM熔化过程特性。主要结论如下：对于基础工况（/=1，=1W），当夹角从0°增加到180°时，PCM 熔化时间先增加、后减少、最后轻微上升。当夹角为0°时，方腔内的PCM 以纯导热形成完成相变，对应的熔化时间为37.87min；夹角为15°时，对应的熔化时间最长，为53.14min，相对纯导热过程增加了40.32%；夹角为120°时，对应的熔化时间最短，为13.97min，相对纯导热过程减少了63.11%。夹角较小时，自然对流对PCM 的整体熔化过程有抑制作用，而只有在夹角大于一定数值时，自然对流才能促进PCM的熔化过程，且多工况计算获取的最优夹角均大于90°。随着腔体长宽比（/）的减小，自然对流对整体熔化时间的抑制作用范围增大，而在较大夹角工况下的促进作用也逐渐下降；随着热流（）增加，自然对流对整体熔化时间的抑制作用变化不大，但在较大夹角工况下的促进作用也明显提升。

ref—— 参考值

upper—— 上限值

w—— 壁面

—— 比热容，J/(kg·K)

—— 液化率

—— 重力加速度，m/s

—— 腔体高度，m

—— 热导率，W/(m·K)

—— 腔体长度，m

—— 糊状区系数

—— 压力，Pa

—— 热流，W/m

—— 温度，K或℃

—— 速度分量，m/s

—— 速度分量，m/s

—— 动力黏度，kg/(m·s)

—— 密度，kg/m

—— 热膨胀系数，1/K

—— 时间，s

—— 强化百分数，%

—— 极小常数

—— 腔体与水平面倾角，（°）

—— 重力与热流方向夹角，（°）

下角标

lower—— 下限值

PCM—— 相变材料