饥饿搜索算法在地下水参数反演中的应用

王文川，薛一铭，徐 雷

（1.华北水利水电大学水资源学院，郑州 450046；2.河海大学水文水资源学院，南京 210024）

0 引 言

区域内某一时段内的地下水资源通常具有随机性和非平稳性特征，对区域水文地质参数（导水系数T 和储水系数S）的精确估计，是进行模拟地下水运动数学模型、科学利用地下水资源的关键。因此，需要研究探讨简便实用的参数反演方法来辅助地下水资源开发利用［1］。一般而言，为获得较为可靠的参数，首先需要进行非稳定流抽水试验，再基于泰斯公式［2］利用试验数据反演分析。目前，传统反演方法有泰斯配线法［3］、改进直线图解法［4］和线性回归法［5］、Jacob 直线图解法［6］和简算法［7］等，但这些方法求解过程复杂，得到的参数可能不是全局最优解。为了更精确地求解参数，近些年来，许多学者已开始将智能优化算法应用于求解参数反演的问题。崔东文［8］将飞蛾火焰优化（Moth-Flame Optimization，MFO）算法应用于含水层参数反演，然而MFO 算法不可避免地存在早熟收敛和全局搜索精度低的缺陷。邱淑伟等［9］利用遍历搜索算法进行求解水文地质参数，避免了陷入局部最优解的情况，求参过程受人主观因素影响较小；但需要多次搜索，当搜索空间范围较大时效率不高。张娟娟［10］采用改进模拟退火算法虽较好地处理了地下水参数反演问题，但其所求得的参数精度不高。陈童［11］等采用自适应的变异因子F和交叉因子CR改进差分进化算法，将其应用于泰斯井函数，较传统差分进化算法寻优率与计算结果精度更高。谭璟［12］设计了一种模拟退火—人工鱼群的混合算法将其应用到地下水模型参数反演问题中。该方法相较原始人工鱼群算法而言，极大地节省了参数计算时间。秋云翔等［13］提出改进的入侵杂草优化算法应用于泰斯模型中，然而当导水系数和储水系数较小时，所得结果适应度和误差值与常用方法接近。

要想得到理想的反演结果，要求智能优化算法具有较好的全局寻优能力和收敛性。随着算法研究的不断发展，近几年涌现出新一批如天鹰优化算法［14］、鲸鱼优化算法［15］、黄金正弦算法［16］以及阿基米德算法［17］等新型算法，它们在基准函数测试上已表现出较强优越性。但“没有免费的午餐”定理在逻辑上证明了没有一种算法可以作为最好的方法解决所有的优化问题。基于此，本文引入Yutao Yang 等人［18］提出的一种新型的饥饿搜索算法，基于两例抽水试验数据［10，19］，利用HGS 算法求解相关水文地质参数，并与以上多种算法反演结果进行比较。本项工作旨在验证HGS 算法在地下水参数反演问题中的可行性和高效性，为其他相关地下水模型研究工作提供参考。

1 基本原理

1.1 算法原理

饥饿是动物生活中决定行为和行动最重要的稳态动机和原因之一。尽管自然界各种各样的刺激和相互竞争的需求总是影响动物的生活质量，但当它们面临热量不足时，它们必须寻找食物。健康的动物比弱小的更容易找到食物来源，有更大的生存机会。饥饿越强烈，对食物的渴望越强烈，机体就越积极地在短时间内寻找食物，当食物来源有限时，为避免因饥饿导致死亡，饥饿的动物之间会有一个寻找食物来源并取得胜利的博弈。基于此，Yang 等人［18］于2021年提出了一种基于群居动物因饥饿进行食物搜索行为的群智能算法——饥饿搜索算法。其数学模型描述如下：

（1）接近食物。社会动物在觅食过程中经常相互合作，但不排除少数个体不参与合作的可能性。以下公式代表了HGS算法在个体合作交流和觅食行为中的核心方程：

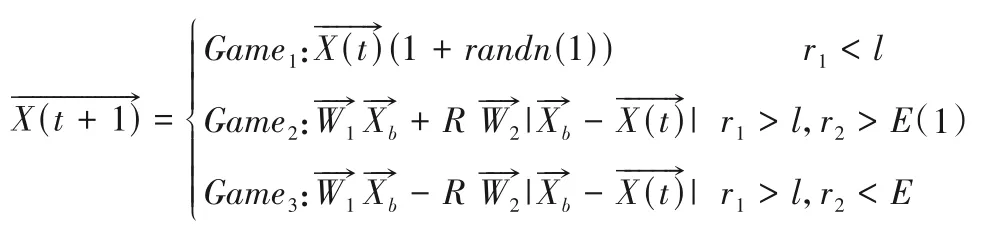
对所有位置的变化控制的E的计算公式如下：

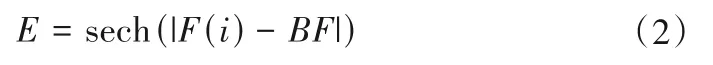
式中：i∈1，2，…，n，F（i）代表每个个体的适应度值；BF是在当前迭代过程中获得的最佳适应度值；sech 是双曲函数，sech(x) =

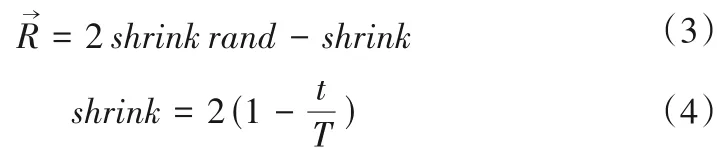
式中：rand∈∀［0，1］；T代表最大迭代数。

式（1）允许个体探索接近最优解的可能位置和远离最优解的位置，在一定程度上保证了对解空间边界内所有位置的搜索多样化。HGS 在搜索过程中，执行式中的Game1可以完成全局搜索，无论是Game2还是Game3都可以完成局部搜索。同样的概念也可以应用于高维搜索空间。

（2）饥饿角色。在这一部分，个体在搜索中的饥饿特征通过一个提出的式（1）进行数学模拟：

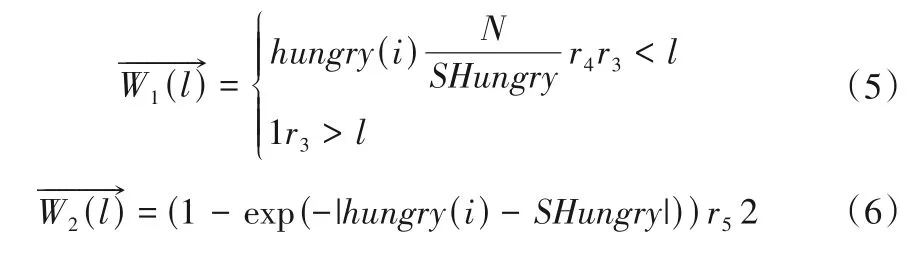
式中：hungry 代表每个个体的饥饿值；N 代表个体的数量；SHungry 所有个体饥饿感的总和，即sum（hungry）；r3，r4，r5∈［0，1］；hungry（i）的公式如下：

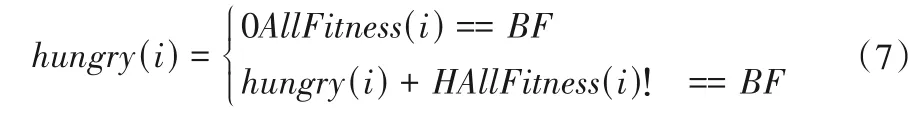
式中：AllFitness（i）是当前迭代过程中第i 个个体的适应度。在每次迭代中，最佳个体的饥饿被设置为0，对于其他个体，新的饥饿（H）是在原有饥饿的基础上增加的，不同个体对应的H 是不同的。H的计算公式为：

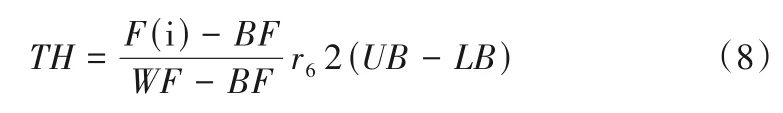
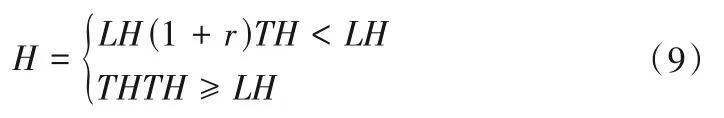
式中：r6∈［0，1］；F（i）代表每个个体的适应值；BF 是当前迭代过程中群体获得的最佳适应度值；而WF 则代表相应的最差适应度值；UB和LB分别为搜索空间的上限和下限；为了使算法得到更好的性能，通过控制饥饿的上下限，LH 为饥饿感H 下限。公式（8）中的UB 和LB 用来反映个体在不同环境中最大的饥饿值；F（i）-BF 代表个体不再需要挨饿的食物量；WF-BF 得出个体在当前过程中的总觅食能力；代表饥饿比率；r6×2代表消除环境因素对饥饿的正面或负面影响。

由于以下独特优势，饥饿搜索算法表现出高效的性能：①参数l 和E 协助HGS 演化初始位置和改变搜索模式，以确保能尽可能地探索整个解空间，并在很大程度上增强算法的多样化能力；②饥饿权重在搜索过程中增加对HGS 的扰动，这两个动态自适应参数可以防止算法陷入局部最优；③参数R→确保以特定的速率减少HGS的搜索步骤，从而满足前期大范围探索目标解空间和后期开发目标搜索深度的需要，在探索和开发两项相反功能之间具有较好的平衡性能；④HGS 可以根据最佳解（和正常解来进化个体位置，以确保更多的探索模式和对解空间隐藏区域的更多覆盖。

1.2 反演模型设计

对于含水层满足泰斯模型的假定条件，在平面上无限延展、均质各向同性的承压含水层中的完整井进行抽水试验，观测井中的水位降深可用泰斯模型的解析解来表示。其模型为［10］：

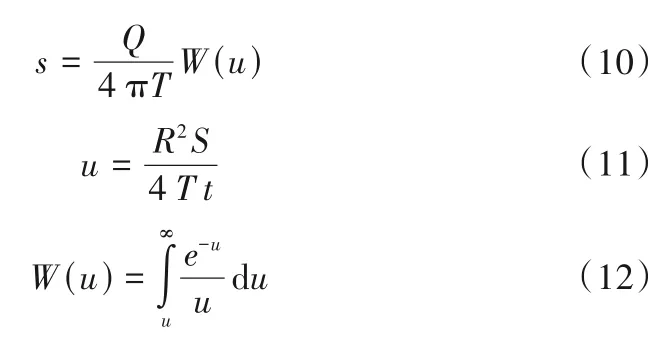
式中：s 为水位降深，m；Q 为抽水井的流量，m3/d；T 为导水系数，m2/d；t为从抽水开始持续的时间，d；W(u)为泰斯井函数；r为计算点到抽水井的距离，m；S 为含水层的储水系数。计算W(u)时需要用广义积分，计算过程将极大增加了算法的运行时间。本文采用Rajesh Srivastava给出的W(u)近似表达式［20］：

当u ≤1时，

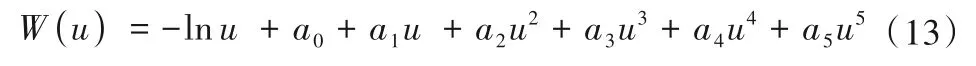
当u ≥1时，

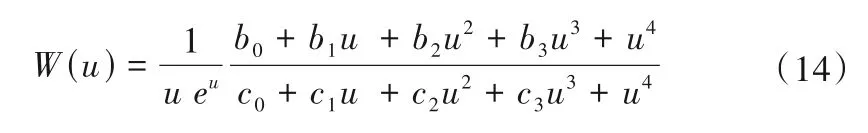
式中：a0=-0.577 22；a1=-0.999 99；a2=-0.249 91；a3=0.055 19；a4=-0.009 76；a5=0.001 08；b0=0.267 77；b1=8.634 76；b2=18.059 02；b3=8.573 33；c0=3.958 50；c1=21.099 65；c2=25.632 96；c3=9.573 32。

因此，在优化算法筛选参数过程中，可按照各时刻实测降深值与模拟降深值的离差平方和的均值构建目标适应度函数：

式中：si为第i 个记录点的实测水位降深，m；N 表示抽水试验的记录点总数。

2 实例应用

2.1 数据来源

为验证本文提出的方法的可靠性，采用2 组实例抽水试验数据进行模型数值验证。实例1数据来源于山东省莱芜县西尚庄地区抽水试验［19］，选择112孔为观测孔，已知测量点距离抽水主井r=104 m，抽水量Q=5.221 9 m3/min，抽水时间t=840 min。实例2数据来源于文献［10］，有一承压含水层做流量抽水试验，假设该含水层的水文地质条件满足泰斯井流模型的假定条件。已知观测孔距抽水井的距离r=100 m，主井做定流量抽水，抽水量Q=162.9 m3/min。利用HGS 算法反演参数（T，S），此外，试验同时采用近年来4种新型优化算法黄金正弦算法（Gold-SA）、天鹰优化算法（AO）、鲸鱼优化算法（WOA）以及阿基米德算法（AOA）对本例进行含水层参数求解［14-17］。

根据大量实验分析，最大迭代次数设置太大导致迭代太长消耗较多计算时间，设置太小迭代太短无法出现最优解。种群取值过大会浪费计算资源，取值太小不能够提供足够采样点。当搜索精度达到一定水平后，迭代次数和种群大小对结果的影响很小，值设置太大会增加计算时间。因此，测试参数设置标准如下：HGS 算法的允许最大迭代次数设为1000，种群大小设为30，根据文献［18］将饥饿感下限LH设置为100，参数l设置为0.03。其他比较算法（包括Gold-SA、AO、WOA 和AOA）的种群大小与允许迭代次数设置均与HGS相同，其他算法特征参数设置参考原始文献［14-17］。根据文献［9］，实例1 中T，S 的搜索空间分别为（4.592×10-4，4.592×106）和（1×10-7，0.5），根据文献［10］，实例2 中T，S 的搜索空间分别为（3，300）和（0.006，0.6）。为了测试各优化算法在求解过程中的稳定性，各方法独立随机运行5次，统计包括最大值、最小值、平均值、中值和标准差在内的五个项目结果，并记录迭代完成时间，相关统计结果见表1和表2。

表1 实例1各方法独立运行5次的统计结果Tab.1 Statistical results of each method running independently for 5 times in Example 1

表2 实例2各方法独立运行5次的统计结果Tab.2 Statistical results of each method running independently for 5 times in Example 2

2.2 评价指标

评价指标采用平均相对误差（MRE）、均方根误差（RMSE）、平均绝对误差（MAE）和纳什效率系数（NSE），计算公式如下所示。以上4 种评价指标可以给出不同方法反演过程的具体表现，例如纳什效率系数越接近于1，表示模型总体质量更好，可信度更高。

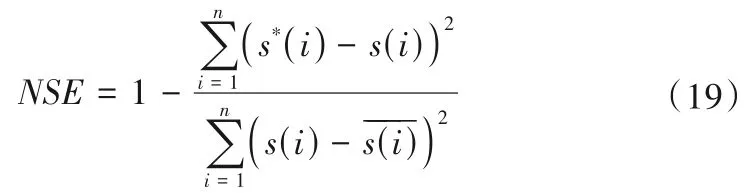
式中：s（i）是实测值；s*（i）是模型的模拟值；n是样本数是实测水位的算数平均值。

2.3 结果分析

各方法的实测降深与理论降深对比图见图1和图2，表3和表4记录了5种方法所得的反演结果和评价指标值。

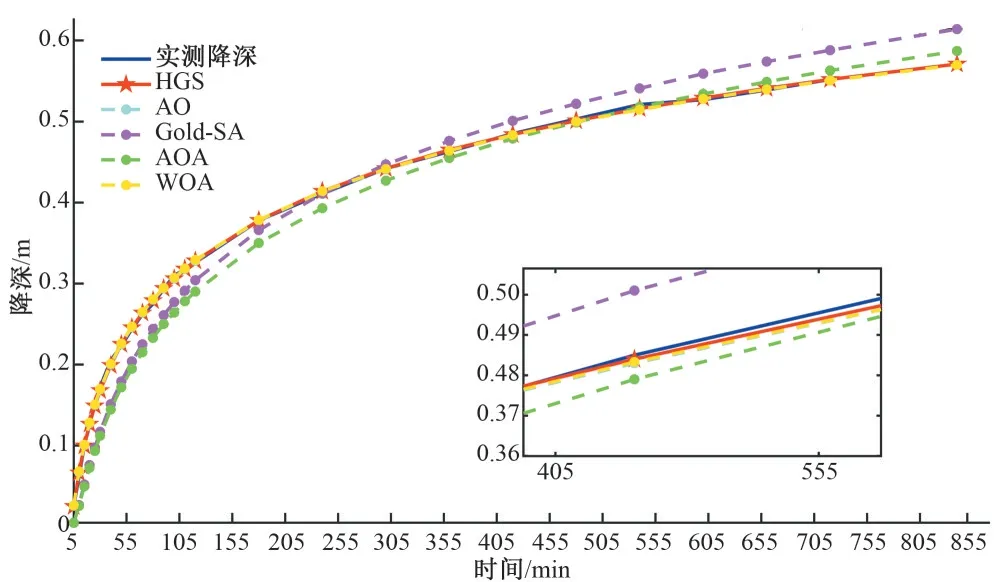
图1 实例1实测降深与模拟降深对比图Fig.1 Comparison of measured and simulated depth drawdown in Example 1

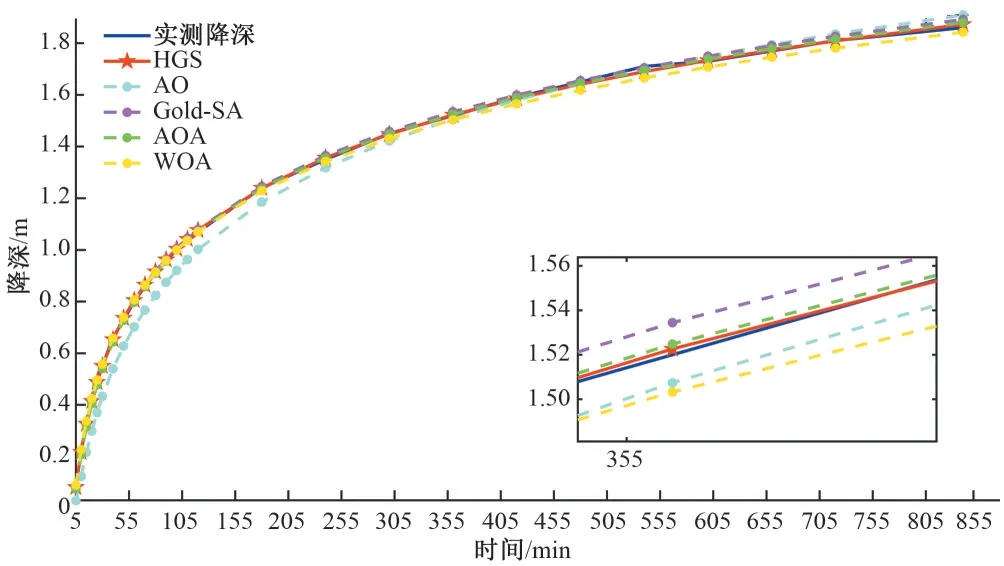
图2 实例2实测降深与模拟降深对比图Fig.2 Comparison of measured and simulated depth drawdown in Example 2

从表1 和表2 中可以得到：①实例1 中，Gold-SA、AO、WOA和AOA 算法获得的最小值分别低于最大值90.47%，92.36%，52.14%，99.16%，实例2 中，Gold-SA、AO、WOA 和AOA 算法获得的最小值分别低于最大值98.21%，59.84%，36.99%，91.51%，HGS 算法运行5 次，其标准差为0，说明HGS 稳健性强；②HGS的迭代时间相较于Gold-SA、AO、WOA 和AOA 算法分别缩短了94.43%，55.91%，27.07%，3.85% 和95.05%，63.16%，35.64%，16.29%，可以看出HGS具有较快的收敛速度。以上结果充分表明HGS 明显优于其余4 种算法，证明HGS 在求解地下水参数问题的有效性和可行性。

根据图1、2、表3 和表4 可以得到：①HGS 算法和其他4 种方法得到的含水层参数值十分接近，可认为利用HGS算法求参的方法是有效可信的；②2 个实例结果均显示HGS 算法的反演精度最高，适应度分别为6.978×10-6和4.347×10-5，实例1中HGS算法较Gold-SA 算法、AO 算法、WOA 算法以及AOA 算法分别提高了99.85%，59.24%，39.16%，99.42%，对于实例2，HGS 算法较其余4 种算法分别提高了96.95%，65.91%，32.29%，99.10%。表明HGS算法具有较为可靠的收敛速度和全局寻优效果；③基于平均相对误差MRE、均方根误差RMSE 和平均绝对误差MAE指标体系下各算法的评可以得价结果，将5 种方法的3 个误差指标值分别从小到大排列为：HGS＜WOA＜AO＜AOA＜Gold-SA以及HGS＜WOA＜AO＜Gold-SA＜AOA。在5 种方法中HGS 算法误差指标数值最小，排名第一，本文采取的HGS 算法具有一定的可行性并处于先进水平；④用HGS 方法求得的Nash-Sutcliffe效率系数值在2组实例中都最接近1.000 0，从图1和图2中可以看出HGS算法预测曲线与实测曲线基本吻合，表明文中提出的方法反演得到的水文地质参数符合相应实际含水层的水力特性。

表3 实例1不同优化方法参数求解结果的比较Tab.3 Comparison of parameter solution results of different optimization methods in Example 1

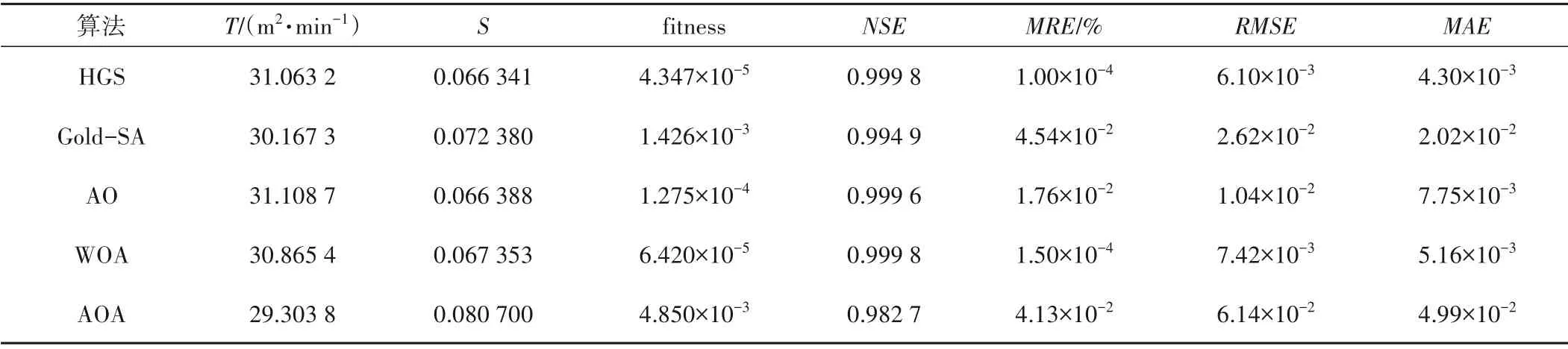
表4 实例2不同优化方法参数求解结果的比较Tab.4 Comparison of parameter solution results of different optimization methods in Example 2

5种方法得到的结果存在差异，对于群智能算法而言，随着迭代次数的增加，种群会不断接近一个最优个体区域，没有确保整个解空间得到搜索，导致算法的多样性丧失。例如，在WOA 中，最优解是猎物的位置，而在位置更新公式中猎物的位置未被充分利用。并且在整个迭代过程中，最优位置只有在出现优于它的位置时才会更新，所以总的更新次数不多，导致算法搜寻效率不高。而在HGS算法中，因为有两个饥饿权重的扰动，在每次迭代后都对种群进行一个干扰，使得其能很好地跳出局部最优。在搜索阶段，可以搜索尽可能完整的解空间，使算法能够在早期达到快速收敛的效果。在开发阶段，可以在附近找到最优解，保证了解的准确性。

3 结 论

本文利用2 组实际抽水试验数据，测试一种新型群体智能优化算法——饥饿搜索算法（HGS）来反演地下水含水层参数。将HGS 算法的计算结果与黄金正弦算法（Gold-SA）、天鹰优化算法（AO）、鲸鱼优化算法（WOA）以及阿基米德算法（AOA）的计算结果对比，可得出以下结论：

（1）在利用算法进行地下水参数反演的过程中，HGS 在较少有限次数内即能快速找到全局最优，具有较快的收敛速度，节省了计算资源。

（2）Gold-SA、AO、WOA 和AOA 算法的实验测试结果均劣于HGS 算法，且HGS 算法多次运行结果的方差为零，弥补了以往采用群体智能优化算法反演地下水参数结果不稳定的不足。

（3）2 个实例中各方法的综合性能从优到劣排列分别为：HGS＞WOA＞AO＞AOA＞Gold-SA 和 HGS＞WOA＞AO＞Gold-SA＞AOA，验证了HGS算法在含水层参数反演的可行性并处于先进水平，HGS可为水文地质参数反演提供新的参考途径。

（4）在后续开展改进群智能优化算法工作中，算法开发阶段可以尝试与饥饿驱动搜索策略相结合，引入两个基于动态自适应参数和可以平衡算法的全局和局部搜索能力，提高算法的寻优性能，以解决更多优化问题。