SWMM径流量计算参数敏感性分析
张 俊,冯慧娟,周 毅,4,李璟冉,周小国,胡 辰
(1.长江生态环保集团有限公司,武汉 430062;2.中国长江三峡集团有限公司,北京 100038;3.武汉大学土木建筑工程学院,武汉 430072;4.海绵城市建设水系统科学湖北省重点实验室(武汉大学),武汉 430072;5.武汉大学水资源与水电工程科学国家重点实验室,武汉 430072)
0 引 言
SWMM 是当前城市排水系统模拟计算的一种主要工具,对雨水径流过程的模拟计算是SWMM 的一项基本功能,SWMM 用户手册中介绍了计算原理和主要参数的取值范围。然而,值得注意的是,模型的准确性不仅取决于对SWMM 中参数含义的准确理解,而且很大程度上取决于参数取值的合理性。SWMM 用户手册提供的参数取值范围较大,因此使用时,不仅需参数率定,且应重点率定高敏感性参数。
SWMM 中的参数分为两类:一类是确定性参数,也称为可测量的参数(例如:管长、标高等);另一类是不确定性参数,又可进一步分为纯经验参数(例如:糙率、洼蓄深度等等)和有一定意义的经验参数(例如:渗透公式参数)[1]。其中的纯经验参数无法测量,只能根据实测资料并结合经验取值。而有一定意义的经验参数,虽然可根据实测资料推理获得,但是因为这些参数的时空变异性较大,很难精确描述,通常用一个近似值代替。
以各参数对径流峰值流量的影响为例,表1 列出了部分研究者对敏感性参数研究得到的排序。

表1 径流峰值流量敏感性参数Tab.1 The sensitivity parameters of peak runoff flow
从表1 所列的敏感性参数看,由于研究对象的差异(例如:不同研究区域、不同降雨过程),哪些参数是敏感参数并无统一认识。常晓栋[13]等人的研究进一步反映了问题的复杂性:SWMM 模型参数的敏感性在不同量级洪水和不同目标函数的情况下表现均不相同,模型参数具有较大的不确定性。
因此,讨论SWMM 参数的敏感性时,必须针对具体区域,“一地一策”地分析。只有在前提条件和区域背景相似的情况下,SWMM参数敏感性的研究成果才有一定普适性。
本研究以产流和汇流过程为主线,首先从降雨过程、下渗过程、地表产流过程以及管道汇流过程多方面定性分析多个不确定性参数对输出量(例如:径流量、峰值流量)的影响程度(即:敏感性),然后结合九江市两河流域的工程案例,分析在该区域利用SWMM建立径流模型的主要敏感性参数。
1 产汇流模块中的主要不确定参数
SWMM 是高度复杂的非线性模型,模型参数间的相互作用使模型敏感参数与模型应用的前提条件密切相关[14]。因此,不确定性参数尽管种类多样,但是对特定前提条件和输出量,并非都有必要进行敏感性分析。在当前的技术条件下,可利用GIS将下垫面和管网信息输入到SWMM模型中。尽管有些数据不够精确,但是在一定的技术条件下,转化结果是确定的,因此本研究将这些参数视为确定性参数,不进行敏感性分析。
与产汇流有关的参数主要是汇水区相关参数、地表透水性能相关参数、降雨径流下渗相关参数、输移过程相关参数[14],其中部分参数属于不确定性参数。
1.1 汇水区性状参数
汇水区性状参数主要包括子汇水区域面积(Area)、子汇水区宽度(Width)和地形坡度(%slope)。
子汇水区域面积在建模之初就已根据基础资料、模型精度要求和建模工作量综合确定,模型建立后属于确定性参数,不再进行敏感性分析。确定子汇水区宽度的方法有多种,但都属于经验法,且取值的差异主要影响汇流时间,而不影响径流总量,在小流域范围内对峰值流量的影响也很弱,因此该参数不作敏感性分析。地形坡度虽然可以对地形基础数据通过信息提取技术转化得到,但是不同的坡度对地表产流的过程有明显影响。因此,计算前将相似地坡的子汇水区作为一类,对同一类的汇水区不做坡度的敏感性分析。
1.2 地表透水性能参数
地表的透水性能参数主要包括不透水面积比(%imperv)、无洼蓄不透水面积比(%zero-imperv)、不透水区蓄水深度(Desimperv)、不透水区糙率(N-imperv)、透水区蓄水深度(Des-imperv)、透水区糙率(N-perv)。
这些参数中,不透水面积比可根据下垫面资料,通过一定技术直接获取,可看作是确定性参数。无洼蓄不透水面积比是个纯经验值,既无法直接观测,也无经验取值可参考,但是从表1 所总结的参考文献看,该参数一直都不属于敏感性参数。根据SWMM 用户手册[15],不透水区蓄水深度是1.27~2.54 mm,透水区蓄水深度范围是2.54~7.62 mm。对于大雨及以上(24 h 降雨25.0 mm 以上)的降雨,由于地表蓄水深度远小于降雨深,对总径流量和峰值流量的影响很小,因此也不属于敏感性参数。实际子汇水区域内透水或不透水下垫面并非均匀一致,不同建模者对下垫面类别的判断及糙率取值也会有主观差异,因此地表糙率是个敏感性参数。
1.3 降雨径流下渗参数
对下渗量的计算如果采用Horton 公式,那么径流下渗参数主要包括最大下渗率(Max.Infilt)、最小下渗率(Min.Infilt)、衰减系数(Decay con)、排干时间(Dry time)。这些参数本来都有准确的物理意义,且应该通过实测获取,但是现场实测不仅耗时耗力,而且参数还有巨大的时空变异性,所以实测的方法并不常用。在建模时,通常简化为根据经验直接取值。
下渗参数是否属于敏感性参数,与雨强大小有一定的关系。降雨强度较小时,下渗过程由雨强决定;降雨强度大到一定程度时,雨水来不及渗透或者土壤含水率很快饱和,下渗相关参数则转变为不敏感参数;只有当降雨强度适中时,下渗过程对产汇流过程的影响明显,下渗相关参数转变为敏感参数。因此,降雨强度较小或较大时,下渗相关参数的敏感性均会降低[14]。只有在降雨强度适中时,讨论下渗参数敏感性才有意义。
1.4 输移过程参数
输移过程参数主要包括管长(length)和管道糙率(roughness)。其中管长是确定性参数。模型中的管道糙率不仅与管材有关,而且还与管道结构性故障和功能性故障程度有关,因此模型中的管渠糙率通常比经验值大。尽管如此,在中小降雨时,雨水系统没有满负荷,糙率只影响峰值出现的时间,对峰值流量和管渠通过的总径流量几乎没有影响。因此,只有在强降雨时,考虑管道糙率的敏感性才有一定意义。
综合来看,要结合特定的研究区域,以特定的降雨为前提,针对具体的输出参数,讨论参数的敏感性才有意义。这也是目前很多SWMM 径流参数敏感性研究成果并无统一结论的主要原因。
2 建模条件与参数敏感性分析方法
2.1 研究区域概况
本研究选取九江市两河(十里河、濂溪河)片区中的部分代表性汇水区域为研究对象。九江两河片区总面积约19.25 km2,覆盖了九江市主要的中心城区,地形整体上南高北低,高差变化较大,最高和最低点的地面高差达到了86 m,主要的排水走向也是从南向北。南边高差变化较大,是新城区的主要扩展方向,片区北部高差相对较小,是中心城区。为了对整个排水区域的雨水径流进行研究,本区域概化为38个排水分区,6 207根雨水管网,6 253 个雨水节点,125 个雨水排口,5 887 个子汇水区,平均每个子汇水区面积为0.327 hm2。
在精度要求较高的模型中,划分的子汇水区面积通常较小,区域内参数的一致性程度较高,其参数的确定性程度也较高。反之,模型精度要求较低、子汇水区域较大的情况下,子汇水区内参数的一致性难以满足,参数有较大的不确定性,同时也成为潜在的敏感性参数。本案例中,子汇水区面积较小,参数的一致性程度较高,参数差异性导致的不确定性程度较低。
地形坡度不仅对地表径流的流速有很大影响,而且也决定了该区域的雨水管渠的坡度,因此需要根据不同坡度划分区域,分别研究参数敏感性。本案例中选取地形坡度不同的三个区域基本情况如表2。

表2 3个代表性区域的基本特征Tab.2 Basic characteristics of the three representative regions
2.2 降雨的选取
对防洪排涝问题和暴雨径流的排除,应该以一定强度的暴雨为前提条件。对年径流总量控制率和年径流污染物冲刷量的研究,应该在全年的降雨过程资料的基础上进行。然而,现有的研究基本上只针对有限场次的降雨(见表1),既没有充分解释所选降雨有何代表性,也无法考虑干旱期下渗能力的恢复程度,导致选取的场次降雨量和雨强的不同对参数敏感性很可能有较大影响。因此,要根据输出参数的不同,区分不同的降雨条件进一步研究。
针对典型年的降雨过程和设计暴雨,按雨量等级划分标准,对连续多场降雨分为小雨、中雨、大雨和暴雨(及以上)4 种级别。其中,对于小雨(24 h降雨量小于10 mm),由于下渗量比例较高,且不形成大量的径流量,所以小雨时的径流特征参数暂不考虑。
综上,中雨及以上强度的降雨发生时,通常关注总径流量和峰值流量,定性分析可知,此时的地表糙率和4个下渗参数最有可能成为敏感性参数;大雨、暴雨(及以上)发生时,此时的地表糙率和管道糙率最有可能成为敏感性参数。
本研究中,为了分析相关敏感性参数的灵敏度,当以总径流量为输出对象时,采用九江市典型年6月1 号-7月31 号长期连续降雨进行径流模拟,选取其中的3 场中雨、2 场大雨、2 场暴雨和这2 个月的连续降雨作为代表性降雨条件;当以峰值流量作为输出对象时,选择典型年同期的2 场大雨、2 场暴雨以及一场设计暴雨作为降雨输入条件。典型年在此时期的代表性降雨情况见表3。
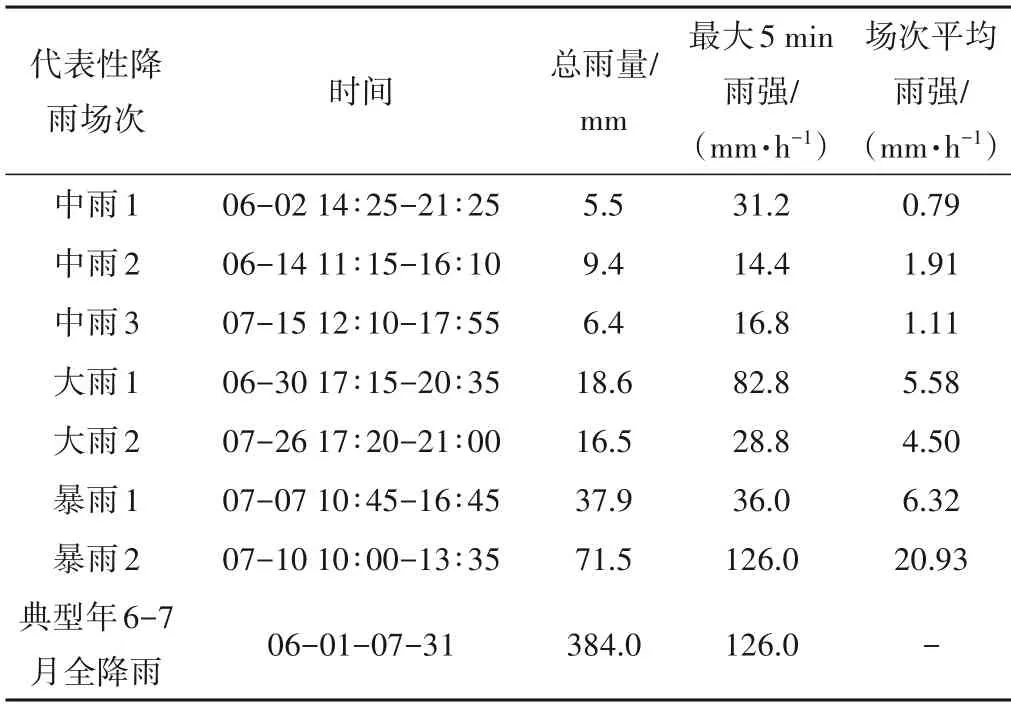
表3 典型年代表性降雨基本情况Tab.3 Basic situation of representative rainfall in a typical year
2.3 参数敏感性分析方法
针对本研究区域,SWMM 模型中不确定性参数的敏感性采用修正的Morris 筛选法进行分析。Morris 法基本原理是:选取单一参数以一定的变化步长进行变化,而其余参数值不变,将多次变化中模型模拟结果的平均变化率记为选取的参数的灵敏度[16]。修正的Morris筛选法计算公式为:
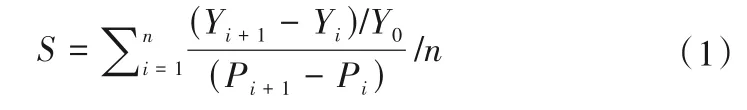
式中:S为灵敏度判别因子;Y0为参数为初始值时模型的输出值;Yi为第i次模拟中模型的输出值;Yi+1为第i+1 次模拟中模型的输出值;Pi为第i次模拟时,运算的参数值相对于参数初始值的相对变化百分率;Pi+1为第i+1 次模拟时,运算的参数值相对于参数初始值的相对变化百分率。
根据参数的灵敏度值,将参数的敏感性分为4类[17]:①当参数灵敏度|S|≥1 时,为高敏感参数;②当参数灵敏度0.2 <|S|≤1 时,为敏感参数;③当参数灵敏度0.05 <|S|≤0.2 为中等敏感参数;④当参数灵敏度0 ≤|S|≤0.05时,为不敏感参数。
所研究参数的物理意义以及取值范围主要依据SWMM 用户手册综合选定,根据取值范围划定的基准值和步长的选取见表4。

表4 SWMM模型水文水力模块参数物理意义及在本研究中的取值情况Tab.4 The physical meaning of hydrology and hydraulic module parameters in SWMM and their values in this study
3 结果与分析
针对所选的3 个不同代表性坡度流域,分别以总径流量和峰值流量为考查对象,对不同级别的降雨,使用修正的Morris敏感度分析公式,计算相关敏感性参数的灵敏度,对其敏感性进行量化分析。
3.1 影响径流总量的参数敏感性
选取典型年同期的3场中雨、2场大雨、2场暴雨以及6-7月连续降雨(如表3),以径流峰值量为考查对象,计算3 个不同坡度的代表区域内的相关参数灵敏度及等级,结果如图1所示。

图1 不同坡度区域径流总量灵敏度计算结果Fig.1 Sensitivity calculation results of total runoff in different slope regions
在图1(a)、(b)、(c)中,部分降雨条件下某些参数灵敏度计算值相同,因此在图中的点位重合。
通过图1 及相关数据,对影响径流总量的多参数敏感性分析发现:
(1)陡坡区A 和中等坡区B:无论何种强度的降雨,也无论是单场还是连续长时间多场次降雨,地表(透水和不透水)糙率和降雨径流下渗的4 个相关参数(最大下渗率、最小下渗率、衰减系数、排干时间)均为不敏感参数。
(2)缓坡区C:在中雨和大雨时,地表糙率和降雨径流下渗的4 个相关参数均为不敏感参数;在暴雨及典型年6-7月全部降雨的条件下,不透水地表糙率为不敏感参数,透水地表糙率以及降雨径流下渗4个相关参数呈现从“高敏感”到“中等敏感”不等的灵敏度。因此,缓坡地形下各参数的灵敏度整体上排序为:最大下渗速率、最小下渗速率、衰减系数>排干时间>透水地表糙率>不透水地表糙率。
由此可见,陡坡和中等坡度地区,这里讨论的6个参数都是不敏感参数。缓坡地区计算暴雨径流量或计算长期雨水径流总量时,下渗的4个相关参数(最大下渗速率、最小下渗速率、衰减系数、排干时间),以及透水地表糙率、不透水地表糙率,都可能成为“敏感”或“中等敏感”参数。
3.2 影响径流峰值的参数敏感性
选取典型年同期的2 场大雨和2 场暴雨,以及1 场设计暴雨,用同样方法,以径流峰值为考查对象,计算相关参数的灵敏度及等级,结果如图2所示。
通过图2 及相关数据,对影响径流峰值的多参数敏感性分析发现:

图2 不同坡度区域径流峰值灵敏度计算结果Fig.2 Calculation results of peak runoff sensitivity in different slope areas
(1)陡坡区A:降雨等级的不同时,不透水地表糙率及管道糙率表现出不同的敏感性,而透水地表糙率表现得不敏感。整体上,该区域的径流峰值流量对各参数的灵敏度排序为:不透水地表糙率、管道糙率>透水地表糙率。
(2)中等坡度区B:降雨等级不同时,影响不透水地表糙率灵敏度的因素复杂,整体上属于中等敏感或不敏感;透水地表糙率是不敏感参数;管道糙率为敏感或中等敏感参数。整体上,各参数的灵敏度排序为:管道糙率>不透水地表糙率>透水地表糙率。
(3)缓坡区C:不同雨量等级下,不透水地表糙率都是不敏感参数;暴雨时透水地表糙率为敏感或中等敏感;大雨和暴雨情况下,管道糙率为敏感或中等敏感。整体上,各参数的灵敏度排序为:管道糙率>透水地表糙率>不透水地表糙率。
由此可见,以径流峰值流量为输出参数时,在陡坡和中等坡度地区,不透水地表糙率和管道糙率较敏感,而缓坡区的透水地表糙率和管道糙率较敏感。这是因为坡度较大时,不仅流速较快,而且主要的汇流和流量输送路径是从不透水地表到管道,而这两个糙率正是决定流速的决定性因素,进一步决定了峰值的大小。坡度平缓时,下渗相对更充分,流速较慢,流量略小,主要的地表汇流路径不仅有不透水地面,而且还有透水地面,因为此时的透水地面更接近饱和而允许更多的径流从表面通过。
3.3 讨 论
讨论SWMM 参数的敏感性时,应该区域基本特征一致性的前提下,有针对性地研究。降雨等级(过程和强度)对产流过程影响很大,并且地形坡度对汇流过程的影响也不可忽视,因此不能忽视这些前提条件,直接进行敏感性分析。作为研究的前提条件,本研究对汇水区的地形坡度和降雨强度进行了分类,确保可能影响敏感性分析的前提条件保持一致。
本研究首先保证分析的前提条件(降雨和坡度)基本一致,然后在汇水区性状参数、地表透水性能参数、降雨径流下渗参数、输移过程参数四类参数中,定性地筛选出影响径流量计算的潜在敏感性参数。进一步地,对每个参数的敏感性程度又进行了量化分析,从而得出结论。因此,只要降雨和坡度条件与本研究一致,研究结论适用于其他地区,有一定的普适性,同时对其他区域用SWMM计算径流量有指导意义。
4 结 论
为了进一步认识SWMM 径流计算不同地形和降雨情况下的参数敏感性,以九江两河片区的部分区域为研究对象,在SWMM 参数敏感性定性分析的基础上,根据地形坡度和雨量等级的不同,对一些潜在的敏感性参数,用修正的Morris法进行了量化分析,结论如下。
(1)以径流总量为输出参数,陡坡区和中等坡度区对地表糙率和降雨径流下渗的参数均不敏感;缓坡区在中雨及大雨情况下对以上参数也不敏感,而缓坡区在暴雨和长期多场次降雨情况下,最大下渗速率、最小下渗速率、衰减系数3个参数属于高敏感或敏感参数,而排干时间属于敏感或中等敏感参数。
(2)以径流峰值流量为输出参数,无论地形和雨量等级有何不同,管道糙率基本上都属于敏感性或中等敏感性参数;在缓坡区且有暴雨时,透水地表糙率也属于敏感性或中等敏感性参数;其余情况下,地表糙率基本都属于中等敏感或不敏感参数。

