基于Copula函数的逐月频率法开展衢江生态流量研究

郑 骞，柳丹霞，兰昱佳，廖 靖

（1.浙江省衢州市农村水利管理中心，浙江衢州 324000；2.浙江省衢州市常山县农村水利管理中心，浙江衢州 324000；3.浙江省衢州市衢江区水利水电技术中心，浙江衢州 324000）

0 引 言

近几十年来我国社会经济迅速发展，河道取水、水库拦蓄、引调水工程等诸多人类水资源开发利用方式改变了河流自然水文情势［1］，从而影响河流生态系统结构与功能的稳定性和完整性，可能会造成河流生态系统的退化［2］。河流水文情势主要表现为河道流量的年际和年内变化［3］，科学合理地确定河道生态流量为保护河流生态系统提供重要理论依据［4］。随着我国生态文明建设的提出，国家进一步推进生态流量保障的相关工作，河流生态需水研究已成为当前水文界以及水利部门的关键课题［5］。

目前，国内外河流生态需水的分析方法主要有水文学法、水力学法、栖息地模拟法和整体分析法等［6］。其中，水文学法以其最简单、快速和经济的特点，在国际上的应用最为广泛，它依据历史水文数据即可确定生态需水。水文学法中国内外常用的几种方法包括Tennant 法［7］（或称Montana 法）、7Q10 法［8］、历史流量曲 线 法［9］（Flow-Duration Curve，FDC）、可变动范围（Range of Variability Approach，RVA）法［10］、最小月平均流量法［11］、逐月最小生态径流法［12］以及逐月频率法［13］等。逐月频率法根据具体河流的水文特征以及生态需求目标选取合理的保证率计算年内各月的生态流量［14］。李捷等［13］将年内各月径流系列的保证率均取50%，计算了伊河的生态流量；娄利华［4］选用的保证率为枯水期取90%，平水期取70%，丰水期取50%，计算了浑河的生态流量。然而，逐月频率法计算河流生态流量时未考虑年均流量与月均流量保证率的差异性，例如枯水年内的月份并不一定都是枯水月份，生态流量计算结果可能偏小，难以保障河流的生态安全。因此，有必要对逐月频率法加以改进，考虑年均流量与月均流量保证率的差异性，使得生态流量的计算结果更加合理。Copula 函数是构造多变量联合分布的一种有效工具，在水文水资源领域应用广泛［15］。利用Copula 函数改进逐月频率法，构建年均流量与月均流量的之间的联合概率分布，既可保留两变量之间的相关性，又可考虑年均流量与月均流量保证率的差异性。

本文基于Copula 函数改进逐月频率法，考虑生态环境的基本保护目标，构建月均流量与年均流量的之间的联合概率分布，建立枯水年型月均流量的条件概率与联合概率的相关关系，针对基本生态流量，将枯水年90%条件概率设为月平均流量的条件概率目标，利用联合概率求解月均流量的保证率，进而推求各月平均流量设计值，并将上述方法应用于衢江生态流量研究，一方面可为衢江水资源开发利用及河流生态环境保护提供依据，另一方面提高生态流量分析成果的合理性，为生态流量计算提供一种有效方法，对其他流域具有一定的借鉴意义。

1 研究区概况与数据

1.1 研究区概况

钱塘江作为浙江省八大水系之一，是浙江省第一大河，流域面积55 558 km2，干流长688 km［16］。钱塘江流域水系及衢州水文站位置如图1所示。

钱塘江水系南源为衢江上游马金溪，至常山港再至衢江，下游经兰江、富春江、钱塘江，最终汇入杭州湾。衢江干流全长82 km，河道平均比降3.1‰。衢江位于钱塘江流域上游，是典型的山溪性河流。衢江径流年内、年际变化较大，4-6月多雨，约占年降水量的50%，汛期时水量陡涨陡落明显，剧烈波动［17］。

1.2 水文数据

选取衢江干流衢州水文站（118.87°E，28.98°N）作为研究衢江生态流量的控制站，衢州站断面以上集水面积约为5 424 km2。收集整理了衢江衢州水文站1956-1990年共35年近自然状态下的逐日平均流量资料，统计年内各月平均流量和年平均流量用于基本生态流量计算。

2 研究方法

2.1 逐月频率法

逐月频率法是根据河流水文情势，结合生态环境需求目标，选取合理的保证率推求年内各月生态流量的计算方法［14］。采用逐月频率法分析衢江基本生态流量过程的具体思路为：基于长系列月平均流量资料，利用皮尔逊Ⅲ型（P-Ⅲ）分布构建各个月份的水文频率曲线；将90%保证率相应的月平均流量作为对应月份的基本生态流量，组成年内不同时段值。

2.2 基于Copula函数的改进逐月频率法

2.2.1 Copula函数理论与基本方法

Copula 函数是定义在［0，1］内均匀分布的多维联合分布函数，可将多个随机变量的边缘分布相连接得到它们的联合分布。根据Sklar 定理［18］，令H 为一个n 维分布函数，其边缘分布为F1，F2，…，Fn，则存在一个n-Copula 函数C，使得∀x∈Rn，满足：H(x1，x2，…，xn)= Cθ[F1(x1)，F2(x2)，…，Fn(xn)]。

Copula 函数主要有椭圆型、二次型、Archimedean 型这3 种类型。Archimedean Copula 函数结构简单，求解简便，被广泛应用于水文多变量联合分析。Gumbel、Clayton、Frank 等函数是常用的二元Archimedean Copula 函数，其中Clayton Copula 函数简单有效的特点突出，且对变量分布下尾部的变化十分敏感，能够准确反映枯水的尾部结构及下尾部相关的变化。因此，本文应用Archimedean Copula 函数族中的Clayton Copula 函数，构建月均流量与年均流量之间的联合分布函数。采用Kendall 秩相关系数τ 来估计Copula 函数的参数θ。Clayton Copula 函数、θ 与τ的关系式为：

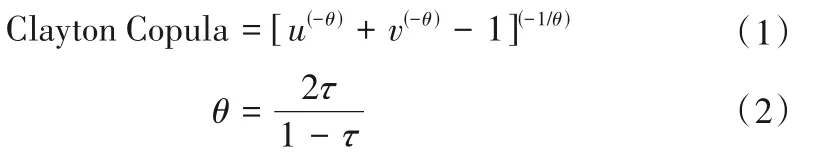
利用均方根误差（RMSE）、相关系数（R）和纳什效率系数（NSE）对边缘分布和联合分布进行拟合优度检验［19］，RMSE 越小、R越大、NSE越大表示拟合精度越高。

2.2.2月平均流量与年平均流量的联合分布建立

确定月平均流量Xm（m 为月序列顺序，m∈N*且m≤12）和年平均流量X0的边缘分布函数FXm(xm)和FX0(x0)。本文Xm和X0的边缘分布函数均采用皮尔逊Ⅲ型（P-Ⅲ）分布。基于边缘分布函数，采用Copula 函数，分别构造月平均流量和年平均流量的二维联合分布函数FXm，X0(xm，x0)：

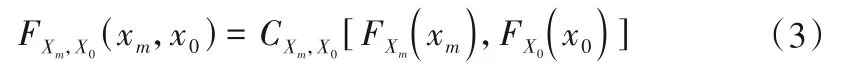
式中：CXm，X0[FXm(xm)，FX0(x0)]为月平均流量与年平均流量的Copula函数。

2.2.3月平均流量的条件概率与联合概率的相关关系建立

根据条件概率的定义，建立枯水年型月平均流量的条件概率与联合概率的相关关系。对于枯水年，可取P（X0≥x0，90%）＝0.9。建立月平均流量的条件概率与联合概率的相关关系：

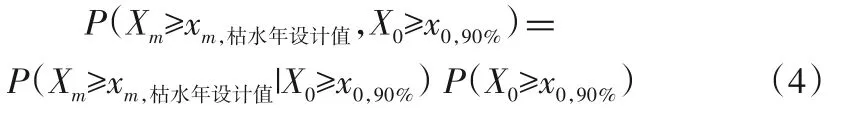
2.2.4月基本生态流量设计值计算

对于基本生态流量，将枯水年90%条件概率设为月平均流量的条件概率目标，推求其相应的指标值作为基本生态流量设计值，即P(Xm≥xm，枯水年设计值|X0≥x0，90%)= 0.9。根据公式（4），由枯水年月平均流量的条件概率与联合概率的相关关系，求解P(Xm≥xm，枯水年设计值，X0≥x0，90%)；根据公式（1）、（2）和（3），由Clayton Copula联合分布函数，求解P(Xm≥xm，枯水年设计值，X0≥x0，90%)对应的月平均流量Xm的P(Xm≥xm，枯水年设计值)；由边缘分布函数FXm(xm)，即各月平均流量的P - Ⅲ分布函数，求解P(Xm≥xm，枯水年设计值)对应的枯水年月平均流量Xm的设计值，即为相应月份的基本生态流量。

2.3 生态流量合理性检验

根据《河湖生态环境需水计算规范》（SL/Z 712-2014）中推荐的河流水系生态环境需水量参考阈值（表1），分析评价基于Copula 函数改进逐月频率法的衢江生态流量计算结果的合理性。根据流域面积，10 万km2以上为大江大河，1 万～10 万km2为较大江河，1万km2以下属于中小河流；根据水资源条件，分为北方河流和南方河流；根据水资源开发利用程度，分为高、中、低开发利用河流。经济社会用水消耗本地地表水资源量不大于20%的为低开发利用河流，大于20%且不大于40%的为中开发利用河流，大于40%为高开发利用河流［20］。

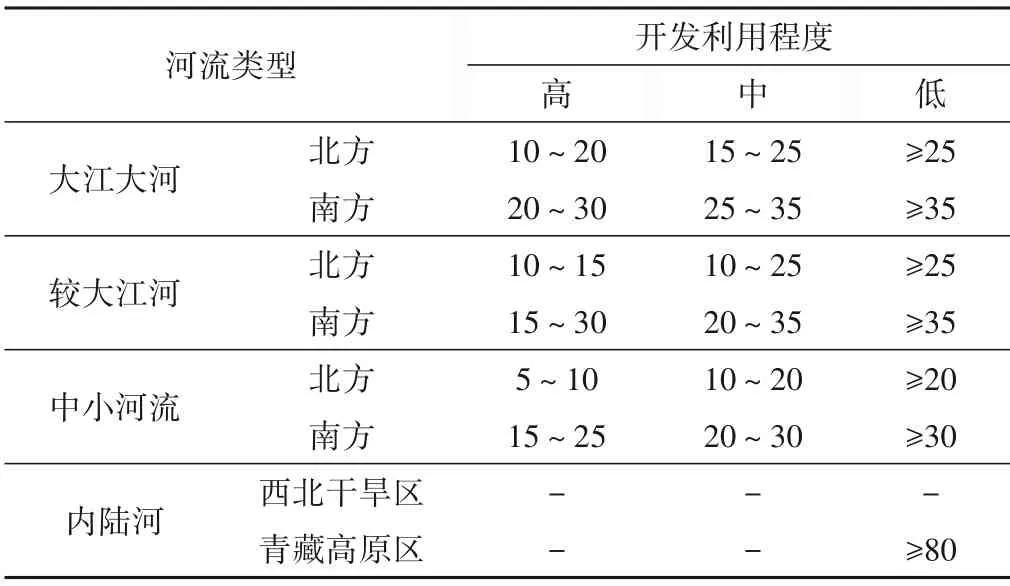
表1 不同类型河流水系基本生态环境需水量参考阈值 %Tab.1 Reference threshold of basic eco-environmental water requirement of different river systems

3 衢江生态流量分析

3.1 联合分布函数分析

衢江月平均流量Xm和年平均流量X0之间的Kendall秩相关系数τ 如表2 所示，各月份月平均流量和年平均流量之间均呈现正相关性。Xm和X0边缘分布拟合优度指标的平均值为RMSE=0.05±0.01、R=0.99±0.01、NSE=0.97±0.02，表明P-Ⅲ型曲线能较好拟合各变量的边缘分布，可进行下一步联合分布分析（表3）。

表2 Xm和X0之间的Kendall秩相关系数τ和Copula函数参数θ计算成果Tab.2 Kendall rank correlation coefficient τ between Xm and X0 and calculation results of Copula function parameter θ

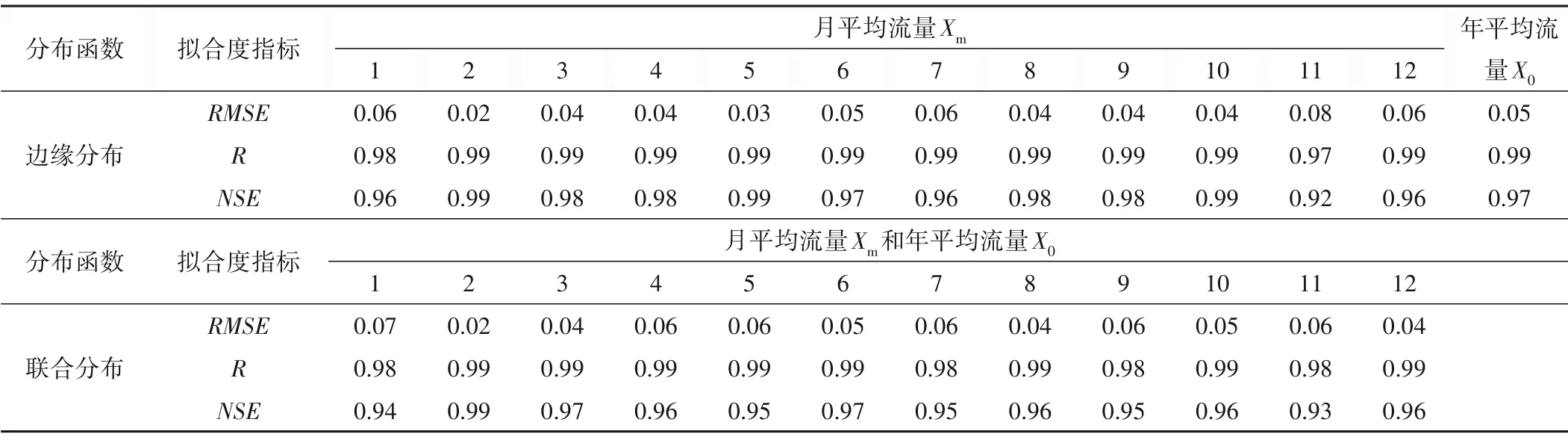
表3 边缘分布函数和Copula联合分布函数拟合优度检验Tab.3 Goodness of fit test of edge distribution function and Copula joint distribution function

建立Xm和X0之间的Clayton Copula 联合概率分布，所有联合分布的不同拟合优度指标（RMSE、R、NSE）的计算结果较为理想，其平均值为RMSE=0.05±0.01、R=0.99±0.00、NSE=0.96±0.02，说明Clayton Copula 函数拟合月均流量与年均流量二维联合分布的结果合理（图2）。

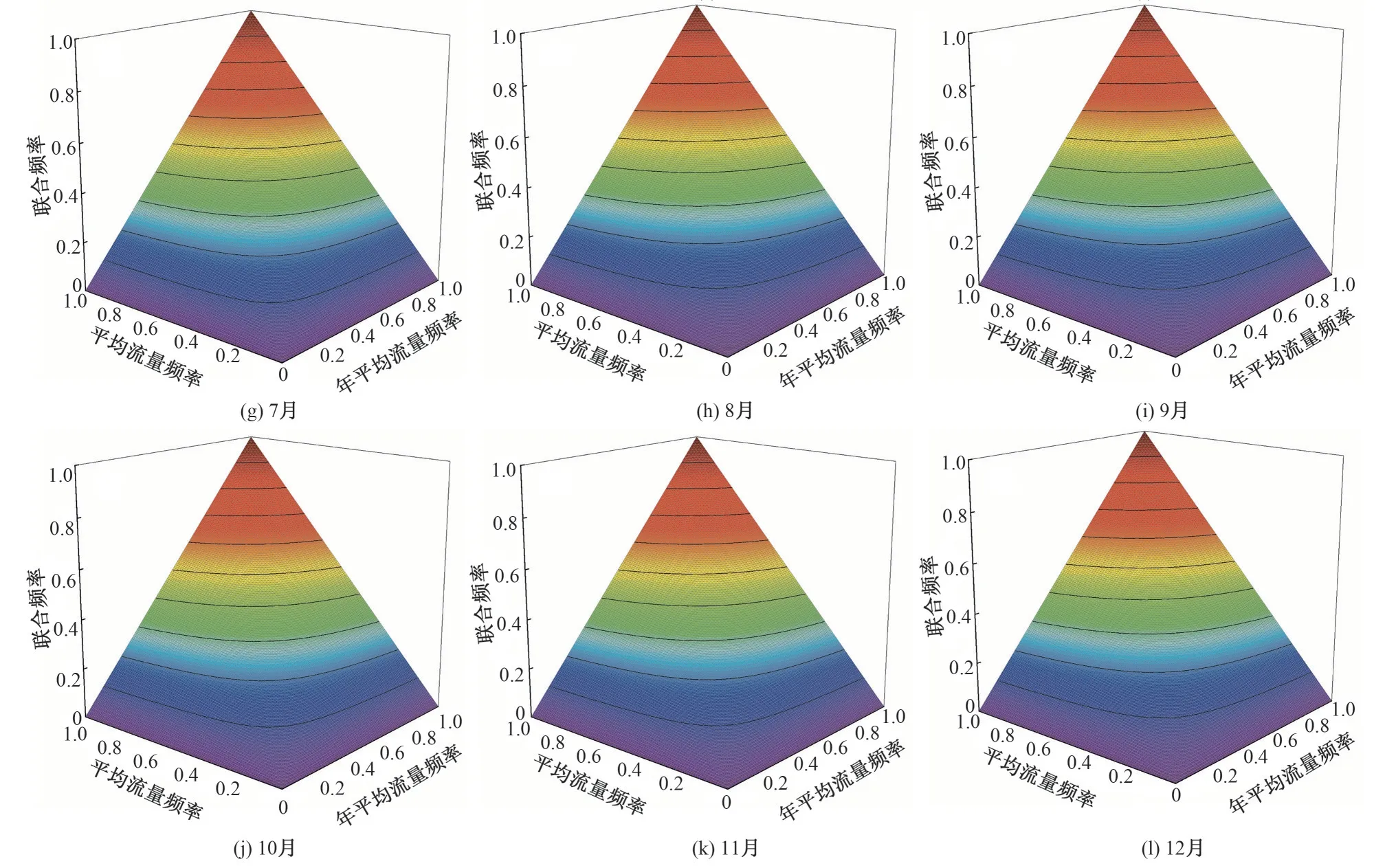
图2 月平均流量与年平均流量联合分布Fig.2 Joint distribution between the monthly mean flow and the annual mean flow

3.2 衢江基本生态流量

将枯水年90%条件概率设为月平均流量的条件概率目标，结合公式（4），基于Copula 函数求解基本生态流量的保证率，结果如表4 所示。各个月份的月均流量保证率有所不同，同时区别于年均流量的保证率。相比传统的逐月频率法，本文提出的基于Copula 函数改进逐月频率法，在计算月均流量保证率时构建了年均流量与月均流量的之间的联合概率分布，在结合年均流量序列与月均流量序列之间的内在相关性的基础上，同时考虑了两者保证率的差异性。

表4 衢江基本生态流量的月均流量保证率Tab.4 Monthly mean flow frequency of the basic ecological flow of Qujiang River

基于月均保证率设计值，利用边缘分布函数FXm(xm)推求基本生态流量。逐月频率法和基于Copula 函数的改进逐月频率法所计算的衢江基本生态流量结果如图3所示。衢江生态流量年内分配不均，5月和6月所需基本生态流量较大，改进逐月频率法能够较为全面合理地反映径流过程的年内变化规律，计算结果较符合河流实际。改进逐月频率法所计算的基本生态流量过程线整体位于逐月频率法所计算的基本生态流量过程线之上，说明改进逐月频率法所计算的基本生态流量高于逐月频率法，在一定程度上更有利于保障河流生态安全。

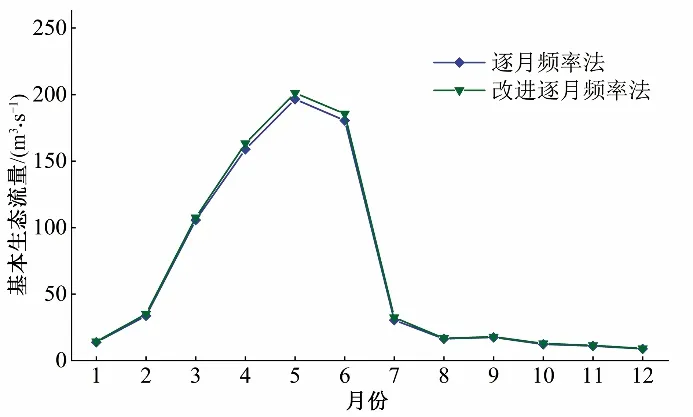
图3 衢江基本生态流量过程Fig.3 Basic ecological flow process of Qujiang River

3.3 衢江生态流量合理性分析

钱塘江位于浙江省，流域面积为55 558 km2。根据地理位置和流域面积，钱塘江属于南方较大江河。衢州市平均水资源利用率为19.5%［21］。根据《钱塘江流域综合规划》中的相关规划，流域内水资源开发利用率不超过35%［22］。考虑当前水资源开发利用情况和未来社会经济发展的用水需求，钱塘江为中开发利用河流。衢江1956-1990年多年平均径流量为58.1 亿m3。基于Copula 函数的改进逐月频率法计算衢江生态流量结果换算成生态环境需水量可知，衢江基本生态环境需水量21.2 亿m3，占多年平均径流量的36%。根据《河湖生态环境需水计算规范》（SL/Z 712-2014），衢江基本生态环境需水量达到了规范的阈值要求，衢江生态流量计算结果具有合理性。因此，基于Copula 函数的改进逐月频率法应用于河流生态需水计算具有可行性，为河流生态需水计算提供了一种有效方法。

4 结 论

基于Copula 函数改进了计算生态流量的逐月频率法，在衢江进行了应用研究，分析了衢江基本生态流量并检验了成果合理性。主要研究结论如下：

（1）Clayton Copula 函数能较好拟合衢江月均流量和年均流量之间的联合分布，拟合优度指标RMSE、R、NSE 均达到较为理想的结果。

（2）基于Copula函数的改进逐月频率法计算得出衢江1-12月基本生态流量依次为14.3、35.1、107.6、163.4、201.3、185.7、32.4、16.8、17.9、12.9、11.5、9.1 m3/s，通过了成果合理性检验，在保障河流的生态安全性角度上计算结果相比逐月频率法偏安全。

（3）基于Copula 函数的改进逐月频率法考虑了河流年均流量与月均流量保证率的差异性，提升了生态流量评估结果的合理性，是生态流量计算的一种有效方法。