基于区间Pythagorean-PROMETHEE算法的水资源配置方案多属性群决策

于弘泽，朱钰婷，治 瑜，张文宇，

（1.中国航天系统科学与工程研究院，北京 100048；2.西安邮电大学，西安 710121）

0 引 言

水资源作为一种基本资源，对社会、经济和生态系统的可持续发展均起着至关重要的作用。然而随着水污染严重、水环境恶化、供需矛盾加剧等诸多环境问题的产生，目前人类相对容易使用的淡水资源仅占世界淡水总储量的0.3%，仅占世界总储量的70万分之一，水资源短缺问题已不容忽视［1］。科学合理地对水资源配置方案进行综合评价，对于实现水资源优化配置和高效利用，以及解决水资源短缺问题具有重要意义。合理的水资源配置方案有助于均衡水资源的分配，实现水资源利用效率的最大化，并能有效解决缺水地区水资源使用困难的问题［2］，因此如何科学选取水资源配置方案成为当下研究热点。郭娇等学者［3］利用AHP-变异系数和模糊物元评价组合的形式对陕西省水资源配置方案进行了综合评价。何英等学者［4］结合优化算法和熵权-TOPSIS 模型，在选取南疆灌区水资源优化配置方案中取得了明显效果。Zhang 等学者［5］建立了一种基于绩效的两阶段分配机制来进行水资源配置方案的选择，该机制显著提高了农业水资源的配置效率。针对决策信息存在的模糊性和不确定性，肖尧等学者［6］采用基于区间犹豫模糊语言与TOPSIS相结合的方法对水资源优化配置方案进行评价和选择。徐冬梅等学者［7］将博弈论、层次分析法和熵权法进行结合，通过建立博弈论格序理论评价模型，应用于雄安新区的水资源配置方案的选取与综合评价中效果显著。考虑到决策过程中出现的特殊数据，孙国营等学者［8］将改进的TOPSIS和灰色关联方法进行结合，实现对不同的水资源配置方案的评价。上述方法虽在一定程度上解决了水资源配置方案的优化选取问题，但水资源配置方案的多属性和不确定性特点增加了方案选取的困难，因此如何量化方案的不确定性信息并实现优劣比较，成为水资源配置方案评估的关键。而Yager 提出的毕达哥拉斯模糊集［9］（Pythagorean Fuzzy Set，PFS）扩大了隶属度和非隶属度的空间范围，对于由人类思维的模糊性和不确定性而做出的决策信息能够实现更加准确的定量化表达，现已被广泛应用于风险评价［10］、应急决策［11］、水资源承载力评价［12］等问题的解决。

综上，本文提出基于区间Pythagorean 模糊语言集和PROMETHEE 方法进行水资源配置方案的决策和评价。该方法首先通过区间Pythagorean 模糊集扩大不确定信息隶属度与非隶属度的空间范围，可以有效解决模糊性决策信息难以定量化表达的问题；其次运用PROMETHEE 方法确定优先函数的类型，实现多个水资源配置方案的优劣比较，从而有效解决S 市水资源配置方案的评价和选择。

1 相关概念

1.1 毕达哥拉斯模糊集

定 义 1［13］：设X为论域 ，称三元组 A ={ x，μA(x)，vA(x)|x ∈X }为X 上的一个毕达哥拉斯模糊集，其中μA：x →[0，1]，vA：x →[0，1]分别表示元素x 属于A 的隶属度和非隶属度，且∀x ∈A 有0 ≤μ2A(x) + v2A(x) ≤1。πA(x) =为x隶属于A的犹豫度。为了简便，Zhang和Xu称(μA(x)，vA(x))为毕达哥拉斯模糊数，表示为(μA，vA)。

定义2：对于一个毕达哥拉斯模糊数p =(μ，v)，则p 的记分函数定义为S(p) = μ2- v2，其中S(p) ∈[-1，1]。p 的精度函数定义为A(p) = μ2+ v2，其中A(p) ∈[0，1]。

设p1，p2为两个毕达哥拉斯模糊数，比较方法如下：

（1）如果S(p1)＜S(p2)，则p1＜p2；

（2）如果S(p1)= S(p2)，则：如果A(p1)＜A(p2)，则p1＜p2，如果A(p1)= A(p2)，则p1～p2。

定义3：设p =(μ，v)，p1=(μ1，v1)，p2=(μ2，v2)为毕达哥拉斯模糊数，运算律定义如下：

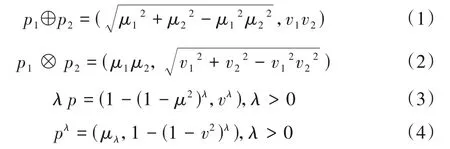
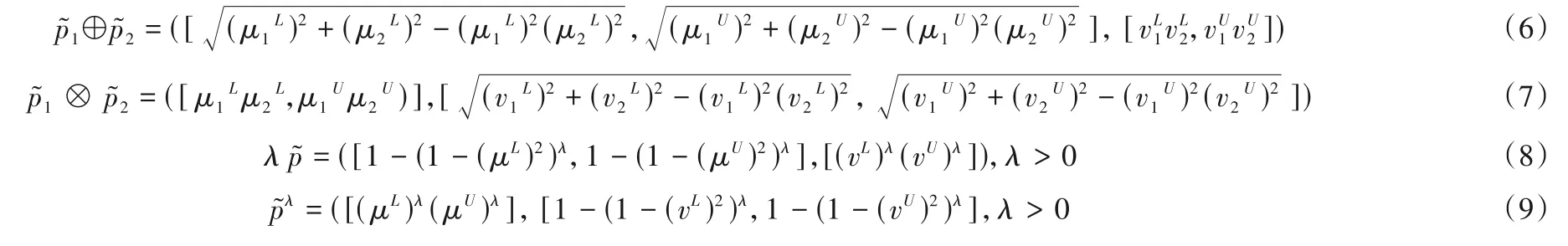
容易证明，区间值毕达哥拉斯模糊数有如下的运算率。

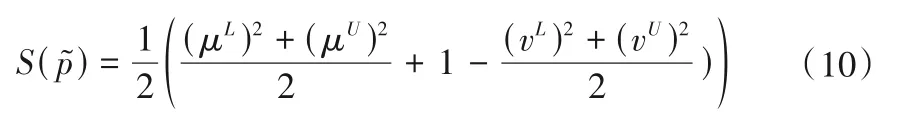
精度函数定义为：

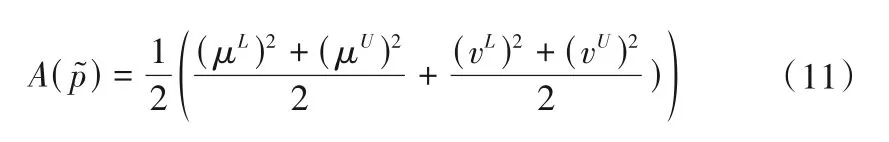
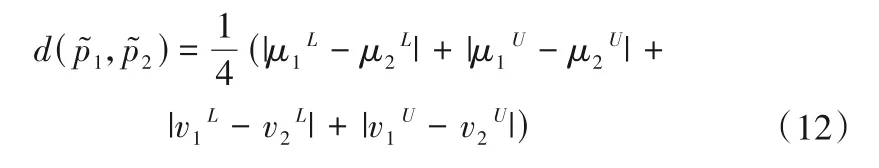
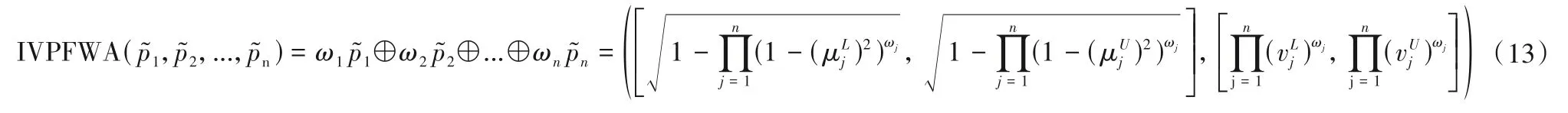
1.2 PROMETHEE方法

PROMETHEE 方法引入优先函数来描述在同一属性Cj上决策关于决策的优先程度，即根据各决策属性值之间差距的大小来判断决策对之间的优劣程度［16］。因此，PROMETHEE 方法对每一个指标定义一个优先函数（不失一般性，设目标或属性为效益型，成本型则意义取反），函数值值域为0～1，函数值越小，方案Ai和Ak之间的差异越小；当函数值为0 时，方案Ai和Ak无差异；其值越接近1，方案Ai优于方案Ak的程度就越高；而当函数值为1时，方案Ai严格优于方案Ak［17］。

2 基于区间Pythagorean模糊-PROMETHEE的多属性决策方法

本节主要介绍了基于区间Pythagorean 模糊集语言的PROMETHEE 方法的算法步骤。首先得到各位决策专家给出的区间模糊评分。其次，我们利用区间Pythagorean 模糊语言的相关知识将其转换成实数，并计算各个决策的流出值、流入值和净流值，根据各对决策的净流值大小，可确定决策间的级别关系从而给出排序，图1给出了该方法相应的流程图。

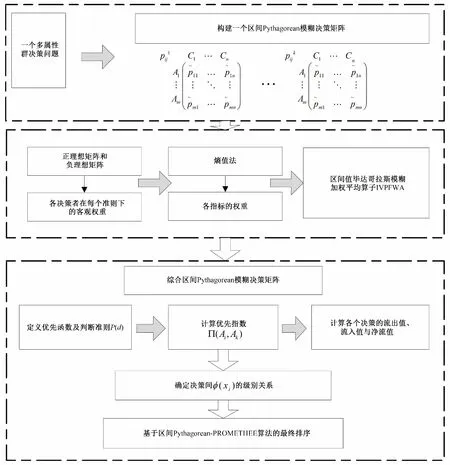
图1 基于区间Pythagorean-PROMETHEE 多属性群决策方法流程图Fig.1 The Flow chart with Interval Pythagorean-PROMETHEE multi-attribute group decision-making method

区间Pythagorean-PROMETHEE 方法主要分为以下几步：

计算每个评价值的贴近度为：

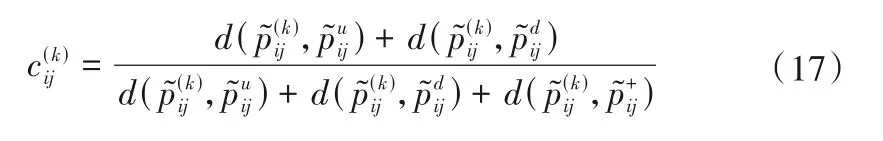
则权重可以确定为：

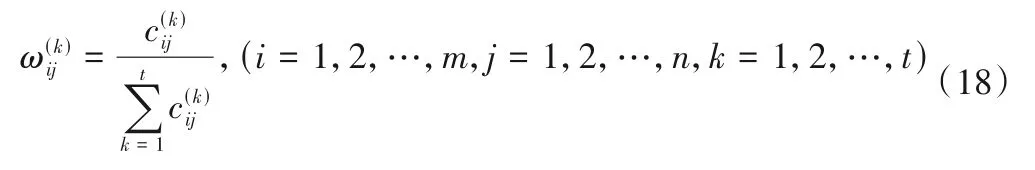
步骤（3）用熵值法计算指标C ={Cj}的权重ωj；

在信息论中，信息熵是对系统无序程度的度量。而在指标矩阵X中，若该项指标的数据差异性越大，则该指标的信息熵越小，指标的权重也就越大；反之，指标的权重越小。所以，可以根据指标信息熵的计算情况确定各指标的权重。熵值权重的计算步骤如下：

（1）用功效系数法对待决策方案的指标数据矩阵X 进行标准化处理

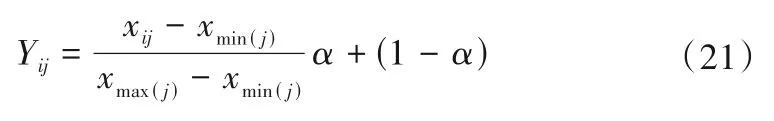
其中，xmax(j)= max(x1j，x2j，…，xnj)，xmin(j)= min(x1j，x2j，…，xnj)，功效系数α ∈(0，1)，功效系数的大小决定功效范围的大小，一般取α = 0.9。

（2）计算指标熵值。假设第j个指标的熵值为ej，则第j个指标的熵值计算公式为：

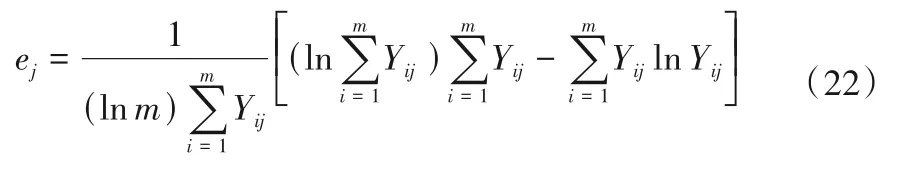
（3）计算指标权重。设第j 个指标的权重为ωj，则权重计算公式如下：

步骤（4）计算优先指数。已知方案集为A ={Ai，i =1，2，…，m}，对于每一对方案Ai，Ak∈A，当决策各属性的权重分别为ωj(j = 1，2，…，m)时，定义其优先指数如下：

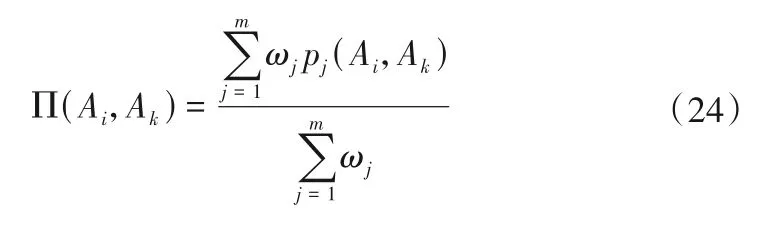
在具体的多属性决策问题中，一旦选定优先函数（即判断准则），就能够求得pj(Ai，Ak)的值，并进而求得Π(Ai，Ak)的值。

步骤（5）计算各个方案的流出、流入和净流值。对每一个方案定义流出、流入和净流。

方案Ai的流出为：

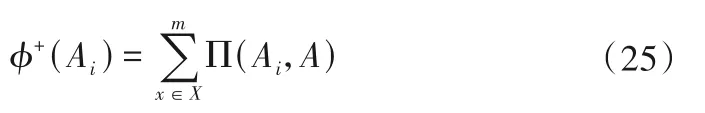
方案Ai的流入为：

方案Ai的净流为：

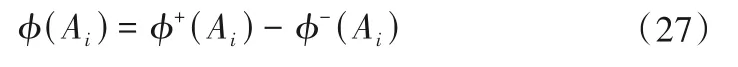
步骤（6）通过计算决策集A上各决策的净流，根据各对决策的净流值大小，可确定决策间的级别关系，即：若φ(Ai)＞φ(Ak)，则Ai的级别高于Ak；若φ(Ai)= φ(Ak)，则Ai与Ak的级别无差异；若φ(Ai)＜φ(Ak)，则Ai的级别低于Ak。

3 案例分析

S市将选取一个最优水资源配置方案以解决目前面临的水资源问题，本节将区间Pythagorean-PROMETHEE 的多属性决策算法应用于S市水资源合理配置方案决策分析中。该案例通过建立实用的水资源配置方案评价指标体系，采用基于区间Pythagorean-PROMETHEE 的多属性决策方法，对水资源配置备选方案从优到劣进行排序，从而选出最优方案。

3.1 水资源配置方案评价指标体系构建

本文以中国S 市水资源配置方案综合评价为例，结合S 市地理位置、社会经济发展水平、水利资源工程开发、水资源利用等客观情况评价各配置方案所实现的水资源利用效果和效益，从社会、经济、资源和效率4个方面综合考虑配置方案的指标体系中每个维度下的具体指标并构建水资源配置方案的评价指标体系C ={Cj}，如表1所示。通过对水资源配置方案的分析筛选，本文共选取8个代表性强且可行性高的水资源配置方案［18］，这些方案重点考虑的是加强各行业节水措施、对现有供水工程优化调配以及污水回用量和海水利用率，各配置方案的评价指标值见表2。

表1 水资源配置方案评价指标体系Tab.1 Evaluation index system of water resources allocation plan

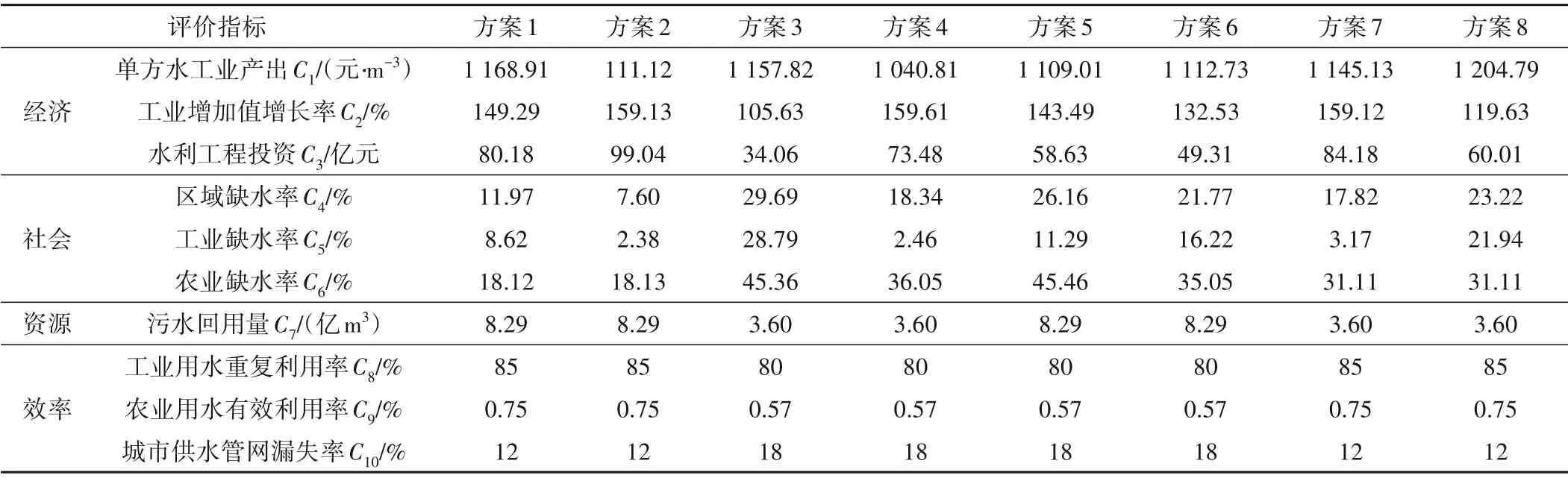
表2 S市水资源配置各方案评价指标值Tab.2 Evaluation index value of each plan of water resources allocation in city S

3.2 案例计算

设S 市的水资源配置方案集为Ai(i = 1，2，…，8)，指标集为C ={Cj，j = 1，2，…，10}，邀请四位S 市的水资源专家包括E1，E2，E3，E4对候选水资源配置方案进行评价。应用本文的算法能够计算候选水资源配置方案优劣程度的排序，并得到S 市的最优水资源配置方案。

（1）决策专家Et根据指标Cj给出八个候选水资源配置方案Ai的评价值构成决策矩阵Dk(k = 1，2，3，4)，表3 表示第一位决策专家的评价值所构成的决策矩阵。

表3 决策专家E1给出的评价矩阵Tab.3 Evaluation matrix given by decision expertE1

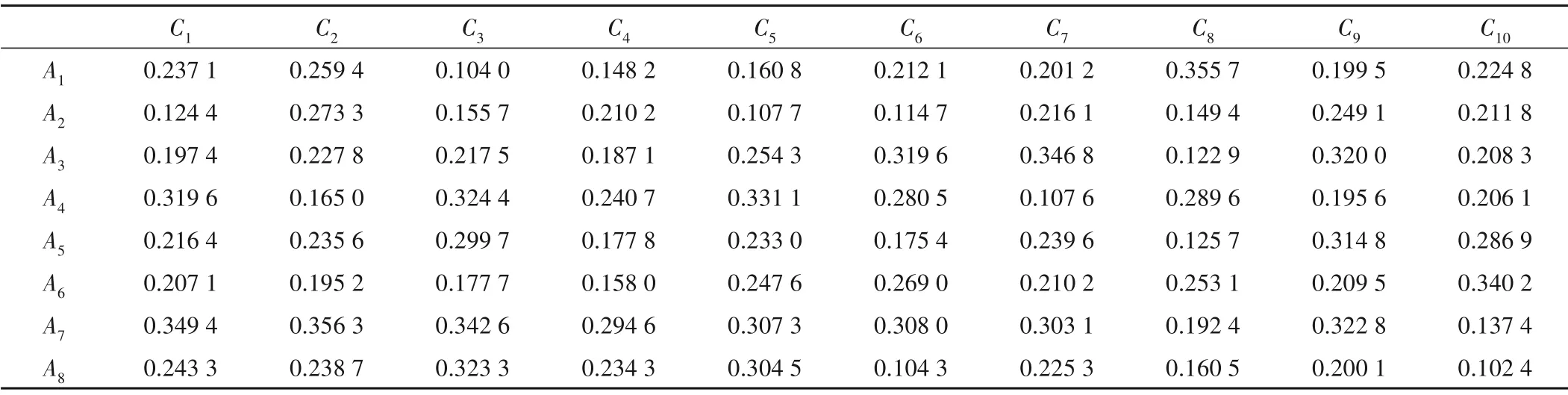
表4 得分函数的综合决策矩阵DSTab.4 Comprehensive matrix of score function DS

（3）用熵值法计算指标C ={Cj}的权重ωj，计算结果如表5所示。

表5 基于熵值法确定的各指标权重Tab.5 The weight of each index determined based on the entropy method

（4）计算优先指数。选择具有线性优先关系准则确定优先函数，按照公式（24）计算每一对方案Ai，Ak∈A 的优先指数Π(Ai，Ak)，结果如表6所示。

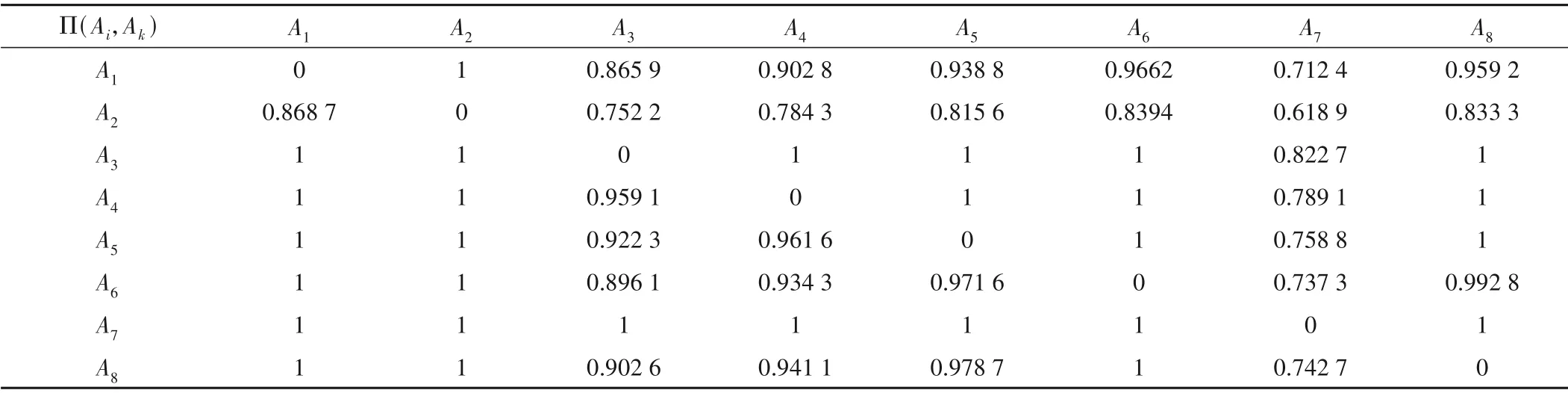
表6 优先指数Π(Ai，Ak)Tab.6 Priority Index Π(Ai，Ak)

（5）按照公式（25）、（26）和（27）计算各个方案的流出、流入和净流值，计算结果如表7所示。

（6）通过计算决策集A上各对决策的流出值、流入值与净流值，对8 个水资源配置方案的综合评价成绩进行排序得：A2＞A1＞A6＞A8＞A5＞A4＞A3＞A7，进而可以确定S 市最优水资源配置方案为A2，即S市对水资源配置的最优推荐方案为方案2。

3.3 结果分析

本文通过运用区间Pythagorean-PROMETHEE 方法对8 个候选水资源配置方案的水资源配置效果进行评价，计算出的净流值φ越大，方案越优。由3.2 节案例计算得到的结果表明（见表7），方案排序为：A2＞A1＞A6＞A8＞A5＞A4＞A3＞A7。方案2 的水资源配置方案效果最好，方案7 的水资源配置方案效果最差。为了对比本文决策方法的有效性与可行性，分别利用TOPSIS与VIKOR 算法对备选方案进行排序比较，每种排序方法的效用值及排序结果如表8所示。

表7 各方案的流出值φ+、流入值φ-和净流值φTab.7 The outflow value φ+，inflow value φ-and net outflow value φ of each plan

由表8 的数值的比较分析可知：不同排序方法所得结果差异不大，但最优方案相同，说明本文决策方法的有效性。TOPSIS［19］方法确定A8优于A6，因为忽略了A8在C2指标下评价不佳。VIKOR［20］方法无法确定A5与A8的具体关系，因为折中理论在计算最终效用值上有局限性。由于区间模糊集的加入，使得本文算法的决策结果更加可靠。从以上结果可以看出，本文应用的区间Pythagorean-PROMETHEE 算法可以解决不同类型的属性信息问题，对于不同的属性权重，得到的决策结果不完全一样，这与实际情况相符，每个候选水资源配置方案都有自己的优势。在实际决策过程中，各属性权重可以根据城市对水资源配置效果的具体需求确定以得到城市的最佳水资源配置方案。

表8 基于效用值各排序方法的比较Tab.8 Comparison of ranking methods based on utility value

4 结 语

针对水资源问题配置方案选取与配置效果等问题越来越呈现出多属性、群决策和不确定性等特征，本文提出了基于区间Pythagorean 与PROMETHEE 方法结合的多属性群决策方法，首先定义了区间Pythagorean 模糊数距离，运用相对贴近系数法以及熵值法确定决策专家与属性的权重；其次，利用综合权重与IVPFWA 算子将各决策矩阵聚合为综合决策矩阵，通过PROMETHEE 方法确定优先函数并通过各决策在某个指标值上的优劣得到最终排序结果；最后，将区间Pythagorean-PROMETHEE的多属性决策算法应用在S市选取水资源配置方案的案例中，案例分析结果验证了该算法的有效性和可靠性。本文提出的区间Pythagorean-PROMETHEE 的多属性决策算法较好地克服了不确定信息在模糊环境中的主观影响，改善了对水资源配置方案评价过程中由模糊不确定性引起的精确性不足的问题，该方法有较强的实用性，有效的提高了水资源配置方案决策的准确性和科学性，是对多属性群决策方法应用于解决水资源配置方案评价问题领域的丰富与发展。