沙坪水电站机组增容改造可行性水力计算研究

向 升，张 清，汤荣才，王 群，鞠小明

（1.四川久隆水电开发有限公司，成都 610000；2.四川省清源工程咨询有限公司，成都 610075；3.四川大学水力学与山区河流开发保护国家重点实验室，成都 610065；4.永城市水利局，河南商丘 476000）

0 引 言

近年来水电行业为响应国家提出的“碳达峰、碳中和”的战略需求，增强水电站调峰调频能力，正大力建设抽水蓄能电站和对运行已久的水电站进行增容改造，提升新能源消纳水平［1］。沙坪水电站位于四川省甘孜藏族自治州九龙县境内，为九龙河“一库五级”梯级开发方案中的第三梯级水电站，2008年建成并投产发电。工程采用引水式开发，正常蓄水位2 187.00 m，引用流量109.6 m3/s，装机容量162 MW（3×54 MW），多年平均年发电量7.801/7.931 亿kWh（单独/联合）。电站水轮发电机组已运行多年，近年来发现机组振动区间增大，水轮机过流部件磨蚀严重，安全运行风险增加。为消除设备缺陷和安全隐患，充分利用水力资源，提高电站年发电量和发电效益，沙坪电站拟进行增容改造，发电机单机容量增加5%，由原来的54.0 MW 增加至56.7 MW，对应水轮机单机额定出力由原来的55.67 MW 增加至58.5 MW。

对机组进行增容改造，可以充分挖掘现有机组的发电能力，使水电站的电网备用发电量增加5%及以上。现代水轮机设备改造设计主要通过以下方式：更换水轮机提高转轮的水力性能［2，3］、运用CFD 技术模拟最优改造方案［2，4］以及应用新材料提高水轮发电机组强度和抗冲蚀性能［3，5］。彭德才等［1］指出水电站增容的方式主要为挖潜增容、设置最大出力和增容改造3种，综述了目前大中型常规电站增容存在的问题，并给出了建议。王照福等［6］采用CFD 技术进行水力方面多目标优化设计，并结合有限元FEA 分析水轮机转轮设计，实现了包括水轮机最优效率、设计工况点效率、汽蚀余量、流量和出力等参数的水轮机整体性能优化。李崇智等［7］根据对港二期电站机电设备的运行性能，分析发现水轮机效率低，过流量严重偏大，提出了更换除蜗壳和尾水管之外的水轮机所有部件方案。王继娥等［8］结合铜街子电站增容大的特点，在轴流式水轮机的水力开发和结构优化方面作了探讨，并优化了三体联吊方案，提高了改造后水轮机的吊装安全性。另外，采用数学解析法推导机组水头、引用流量和出力三者之间的最优化关系，充分提高机组的效率［9］。

本文基于沙坪电站现有的布置形式，在不改变原引水流道和机组基础埋设部件的前提下，根据实测上下游水位和水轮机运行水头，应用实际电站运行水位下多机组水轮机出力计算公式来反演计算实际引水隧洞的水力损失，然后分析电站的增容能力。

1 机组增容能力计算分析方法

沙坪电站增容改造的前提条件是不改变原有水工建筑物，包括大坝高度和原有输水发电系统建筑物。在电站水库运行水位不变的条件下，机组增容能力的大小主要决定于机组的水头、流量和效率的富裕量。而机组水头除与水库水位和尾水水位有关外，还与有压输水管道的实际糙率值有关，流量和效率与机组特性有关，这几个参数共同决定了机组增容能力的大小。

了解现有电站的运行状态，对确定增容能力是有帮助的，图1 绘制了沙坪电站引水发电系统布置的示意图，共由3 台机组组成，每段管道按顺序编号。为准确判断沙坪电站可以增加的机组容量大小，需要分析现有电站的运行记录资料，以准确计算输水隧洞的实际糙率值。对于布置有多台机组的引水式水电站，可以根据电站的布置方式，计算出对应水库水位和机组出力下的每台机组的引用流量、工作水头和水轮机效率值，其计算方法如下。

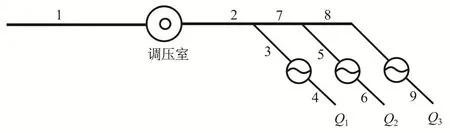
图1 沙坪水电站发电引水系统布置示意图Fig.1 Sketch of power generation diversion system of Shaping Hydropower Station

根据上述引水系统布置计算简图，可以列出三台水轮机出力计算公式：

其中第一项为上游水库水位，第二项为厂房下游尾水位，第三项为引水隧洞和压力钢管主管中的水头损失，第四项和第五项为支管和尾水道中的水头损失。式中N、H、Q 和η 分别为水轮机的出力、水头、流量和效率；∇上和∇下为上游和下游水位；L、A、d 和λ 分别为每段管道的长度、面积、直径和沿程水头损失系数，对于已经完建的水电站工程，这些输水系统布置参数是确定的。

将上述公式（4）、（5）和（6）分别代入出力计算公式（1）、（2）和（3）中，给定3 台机组出力并先假定水轮机效率，得到仅包含3台机组流量为未知量的3元二次代数方程组：

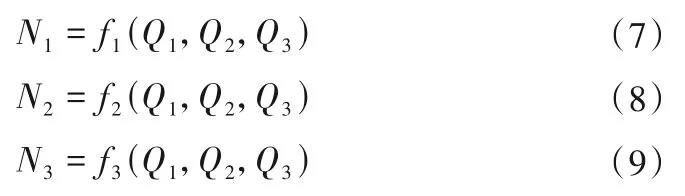
用数值计算方法求解上述方程组，可以得到相应的机组流量，进而计算水头，算出单位转速和单位流量，再在水轮机模型综合特性曲线上插值得到水轮机效率，与原先假定的效率进行比较，若不相等，继续以新的水轮机效率代入后重新计算，直到插值得到的效率与前一次假定的效率基本相等为止，该迭代计算工作通过编写程序由计算机插值自动计算完成，其中水轮机模型综合特性曲线采用网格数据点的方式进行数字化，存储在计算文件中。

压力引水道的沿程水头损失采用谢才—曼宁公式计算：

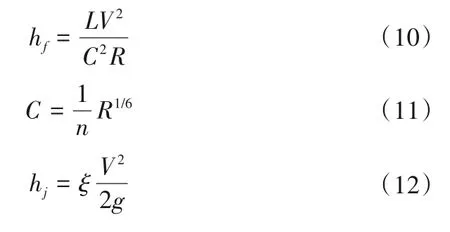
式中：R 为水力半径；n 为引水道的糙率；ξ 为局部水力损失系数。

水轮发电机组负荷变化时调压井的水力过渡过程根据特征线法结合调压室的边界条件，获得调压室的最高和最低涌浪水位及波动过程［10-12］。关于机组负荷变化后的调节保证复核计算以及输水系统过渡过程计算原理和方法可参考相关文献资料［13-15］。

电站增容能力计算就是根据给定的机组出力，计算出稳定运行状态下各台机组的流量、水头和效率，确定水轮机运行工况点，判断增容能力的可行性，同时也可以计算调压井的水位值。

2 数学模型验证

沙坪水电站2008年已经建成并投产发电，本次电站水轮机扩容改造涉及到机组引用流量增加和水头变化。为了验证电站计算模型中引水系统水力参数选取的合理性，电站运行人员分别随机的对不同水库水位下1 台机组运行、2 台机组运行以及3 台机组运行的水轮机蜗壳压力进行了现场测量，同时也测量了1 台机组运行和2 台机组运行时的调压井水位，这些实测数据为采用数学模型分析机组增容能力提供了最直接和最可靠的计算基础资料，可用来检验数学模型对引水系统水力学参数选取的准确性。下面将现场记录的调压室运行水位、水轮机运行水头数据与数学模型模拟结果进行对比分析。

2.1 调压室水位

根据水轮机出力公式反演获得了各段管道的糙率和水头损失，数学模型中采用钢筋混凝土衬砌的管道糙率取0.014，根据《水工隧道设计规范》（DL/T5195-2004）［16］，钢筋混凝土衬砌的管道糙率在0.012～0.016之间；采用光面爆破法进行喷锚支护的管道取0.022，规范建议的糙率在0.020～0.025之间；采用普通钻爆法进行喷锚支护的管道取0.025 7，规范建议的糙率在0.025～0.030 之间；压力钢管段的糙率取0.012，规范规定的糙率在0.011～0.013 之间。以上推算的电站实际运行管道的糙率均在规范建议的范围内，说明采用上述糙率来进行计算是合理的。由于电站实际运行时无法准确获知各管道的局部水头损失系数，因此本文在计算时是把局部水头损失合计到总水头损失中。采用此数学模型对电站稳定运行工况下调压室水位进行了计算，实测数据和数学模型计算值对比如表1所示。

表1 调压室运行水位数学模型验证Tab.1 Verification of mathematical model by operation water level of surge chamber

由表1 调压井水位实测数据与模型计算结果分析可知，实测调压井水位和数学模型计算值的平均偏差在0.19 m 左右，考虑到平时调压井运行水位的波动范围，这样的误差在可接受的范围内，因此电站无论是1 台机组运行、2 台机组运行或者3 台机组运行，数学模型采用的引水隧洞糙率值基本符合电站实际情况。

2.2 水轮机水头

根据现场实测的蜗壳压力P蜗，可按照以下的公式计算获得水轮机的工作水头：

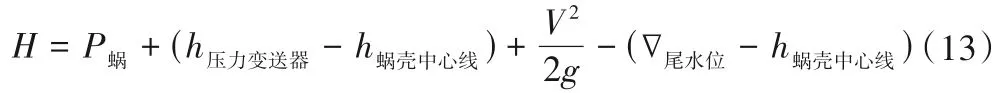
式中：P蜗为压力变送器测量的压力读数，m；h压力变送器为蜗壳进口压力变送器安装高程，取2 000.03 m；h蜗壳中心线表示蜗壳中心线高程，取1 997.23 m。

此外，蝶阀前压力变送器安装高程2 000.73 m，计算时采用1 MPa=101.94 mH2O。表2 对比了不同时刻记录的单台机运行下水轮机水头实测值和数学模型计算值，图2 绘制了相对于实测值±0.5%误差下的分布图。

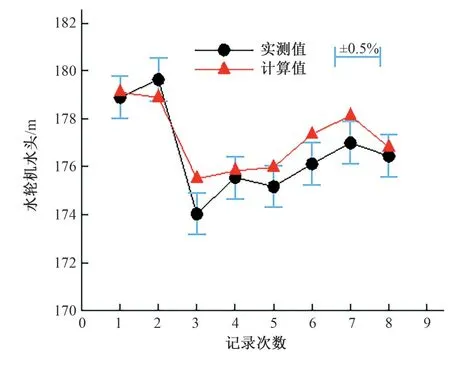
图2 单台机组运行下水轮机水头实测值与计算值误差比较Fig.2 The error comparisons between measured and calculated water head under single unit operation

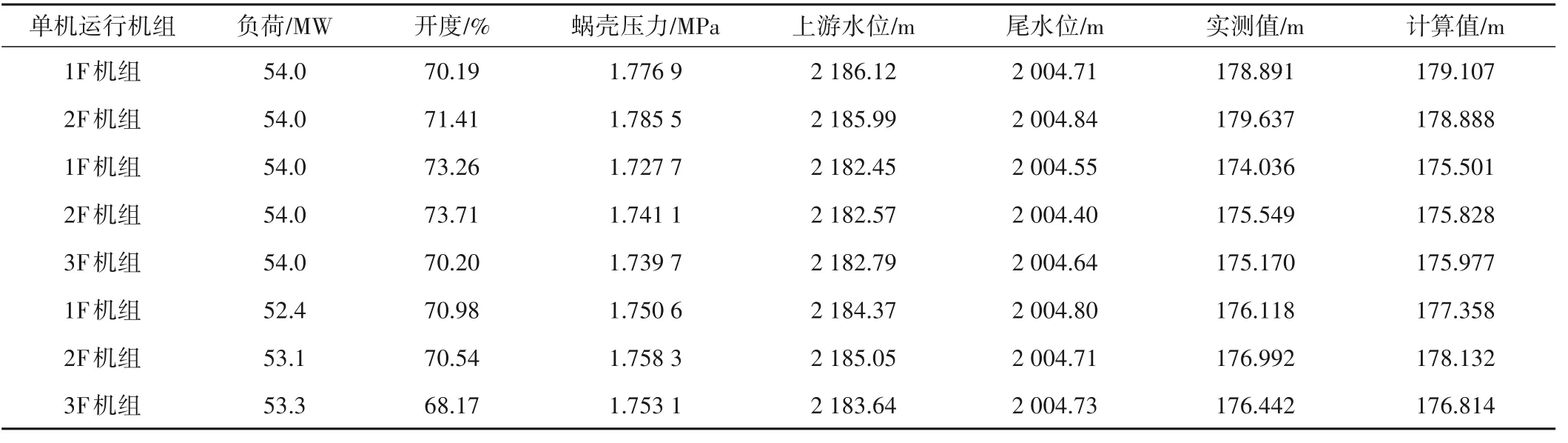
表2 单台机运行下水轮机水头实测值和计算值比较Tab.2 Comparison of measured and calculated water head of a single turbine operation

同样的，根据水电站记录的2 台机和3 台机组联合运行下的水轮机运行参数，采用本文数学模型计算了水轮机的水头。图3 所示分别展示了2 台机和3 台机实测值和计算值的误差比较，图中的2 台机组和3 台机组的误差线分别设置为±0.5%和±1.5%。

由图2 和图3 可知，在单台机组运行和2 台机组联合运行下，水轮机水头实测值和计算值的误差在0.5%范围内，误差平均值为0.1%。当增大引用流量至3 台机组联合运行时，实测值和计算值的误差小于1.5%，误差平均值为0.9%。由此可知，综合考虑上述1台机运行、2台机组运行和3台机组运行时的水轮机工作水头，数学模型计算得到的各种运行工况水轮机工作水头基本与现场实测数值一致，说明数学模型可以用来计算分析沙坪水电站的机组增容能力，并且可以用来复核改造后的电站调节保证值以及输水系统水力过渡过程计算，数学模型基本能够反映电站实际运行工况。

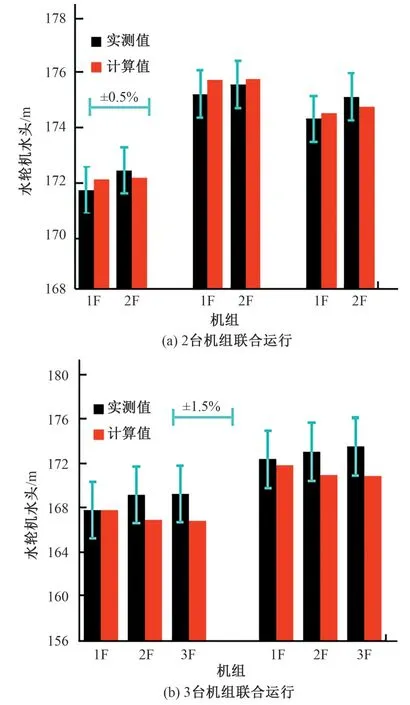
图3 2台和3台机组联合运行下的水轮机水头实测值和计算值误差比较Fig.3 Error comparisons between measured and calculated water head of turbine under combined operation of two and three units

2.3 讨 论

由上述结果可知，当引用流量较小即1 台或者2 台机组运行时，计算值与实测值的误差很小。当3台机组联合运行时，上述数值计算的结果与实测值相比，两者差异最大增大到1.5%。分析其中误差增大的原因，可能包括这几个方面：①蜗壳压力表读取的数值为各记录工况下的读数平均值，尾水位也为记录的平均值，考虑到电站实测压力的变化，在读数或测量时可能存在误差；②水电站引用流量大，各工况机组运行时不能准确测定机组过流量，在计算流速水头时只能按照机组设计时额定流量获得，而额定流量可能与实际过流流量存在差别。当3 台机组联合运行时，流量增大，实际的过流量与真实值之间差异增大，导致数值模型计算结果与实测值的误差增加。尽管如此，只要是在额定出力附近记录的数据，即使流量有些误差，也不会影响太大，可以认为基本能够反映当时水轮机的工作状态。③上述公式（1）中的水轮机效率是根据特性曲线的模型效率换算得到的原型水轮机效率，原型和模型效率换算可能也会存在一定的误差。

3 机组增容能力计算

按照机组增容5%计算，水轮机增容到58.5 MW，发电机额定出力增加到56.7 MW。考虑到沙坪水电站水库最多运行时间的较低蓄水位为2 183.00 m，水轮机直径为2.03 m，按照上述验证过的数学模型初始工况计算模型，分别进行水轮机增容前和增容后的额定出力计算，计算结果如表3所示，表中效率是转轮综合特性曲线上的效率，不是电站实测效率。

由表3可知，如果保持转轮直径2.03 m不变，仍然采用原转轮型号，在水库最长时间运行的较低水位2 183.00 m，单机额定出力从55.67 MW 增加到58.50 MW，机组引用流量会增加，三台机的总引用流量将由106.263 m3/s 增加到114.162 m3/s，并且效率还略有下降。若考虑水轮机转轮直径增加，可以增大过流能力，或者说同样的出力下，机组引用流量可以不用增加太多即可达到增容出力要求。如果不加大转轮直径，只能靠增加引用流量来扩容，然而原机组的引水流道已经施工完成，难以改变，若强行增加引用流量有可能会导致水轮机效率降低。因此综合考虑现有基坑尺寸，可适当增大转轮直径，这样有利于减小流量增加的幅值，提高水轮机的工作水头。特别是对于引水式电站，流量的增加对水轮机工作水头很敏感，根据基坑尺寸和固定导叶位置，结合机组厂家设计图纸，建议将转轮直径增大至2.10 m。直径增大后，经计算，增容后的三台机的总引用流量为112.375 m3/s，效率仍然在94.58%～94.72%。然而相比于原直径水轮机增容后的引用流量，直径增加后的引用流量变化不是很明显，这是因为对于2.10 m 直径的转轮，在计算时仍然采用的是原直径水轮机的模型参数。目的是给出一个在适当增加转轮直径后可减小引用流量这样一个建议，若采用比旧转轮效率更高的新转轮，直径增大后流量变化会更明显，为电站设计人员在增容改造选择新转轮时提供一定参考，方便业主最终选择增容改造的水轮机型号。由于沙坪电站属于已建电站，水轮机基坑直径已经固定，只能按照当前基坑能承受的水轮机尺寸来设计新转轮，当转轮直径不能再增大时，提高水轮机效率成了增加出力的有效措施。

表3 增容前和增容后水轮机额定出力计算表Tab.3 Calculation of turbine rated output before and after capacity increasing

4 调压井水位复核计算

电站扩容改造后，相比原机组引用流量有所增大，电站引水系统水工建筑物保留不变，需要复核电站引水发电系统的水力过渡过程计算结果，特别是调压井的涌浪水位复核和电站调节保证复核至关重要，电站增容后仍然需要满足原来的电站的各项设计要求，确保原有水工建筑物、压力钢管及新机组能够安全运行。

4.1 调压井最高涌浪水位计算

根据《水电站调压室设计规范》［16］，调压室最高涌浪水位计算需要考虑水库最高水位时电站3 台机组丢弃全部负荷的工况，并且引水系统糙率应取可能的最小值。设计规范中调压室最高涌浪水位计算要求隧洞取最小糙率的原因，就是考虑到电站施工后引水隧洞糙率可能存在一些变化。对于沙坪水电站，已经建成发电多年，引水隧洞糙率在前期已经通过实测调压井水位和水轮机工作水头得到了验证和检验，因此增容改造计算中引水隧洞糙率取值按照已经验证过的现场实测糙率进行计算，这样比较符合实际电站扩容改造后的运行情形。沙坪电站水库最高水位取正常蓄水位2 187.00 m，3台机组发电机额定负荷56.7 MW 运行（水轮机出力58.5 MW），丢弃全部负荷后，调压井的涌浪水位变化过程如图4所示。

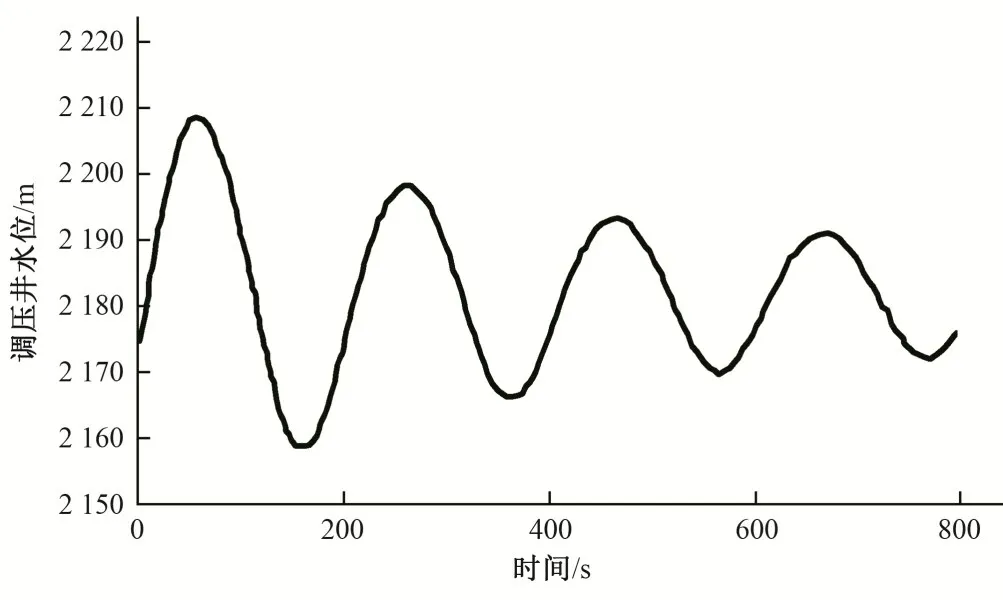
图4 3台机同时丢弃全部负荷的调压井水位变化图Fig.4 Water level change diagram of surge chamber with all loads discarded by three units

由图4 可知，3 台机组全部丢弃负荷后，调压井的最高涌浪水位2 213.164 m，低于调压井通气洞底板高程7.34 m；最低涌浪水位为2 164.836 m，高于调压井井筒底板10.34 m。就最高涌浪水位而言，增容改造后调压井最高涌浪水位是安全的，并且还有比较大的安全富裕。根据计算，即使考虑引水隧洞糙率有变化，采用规范要求的可能最小糙率计算，最高涌浪水位增加的幅值也仅有1.0 m 左右。可以得到结论：沙坪电站增容改造后调压井最高涌浪水位仍然满足设计规范要求，调压井运行是安全的。

4.2 调压井最低涌浪水位计算

调压井最低涌浪水位计算的工况为电站水库最低运行水位2 181.50 m，电站2台机组运行，第3台机组流量由0增加至额定流量。并且需要对水库最低水位时3台机组丢弃负荷后的调压井第二振幅进行核查，取两者中的最低值作为调压井的最低涌浪水位。计算工况取最低运行水位2 181.50 m，2台机组发电机额定负荷56.7 MW 运行（水轮机58.5 MW），由2台到3台增负荷，调压井的水位变化如图5 所示，同时也绘制了3 台机组运行同时丢弃全部负荷后的调压室水位变化过程。可以看出，当由2 台机增至3 台机时，调压井最低涌浪水位2 165.188 m，高于调压井井筒底板2 154.50 m，水深为10.69 m。丢弃全部负荷后，调压井最高涌浪水位2 208.711 m，最低涌浪水位2 158.461 m。丢弃负荷第二振幅的最低涌浪水位仍然高于调压井井筒底板2 154.50 m，水深3.96 m。满足设计规范要求的大于2.0 m 水深要求，增容后调压井最低涌浪水位是安全的。综上所述，电站增容改造后，无论是电站机组丢弃负荷还是电站机组增负荷，原设计的阻抗式调压井仍然可以满足设计规范要求，运行是安全的。

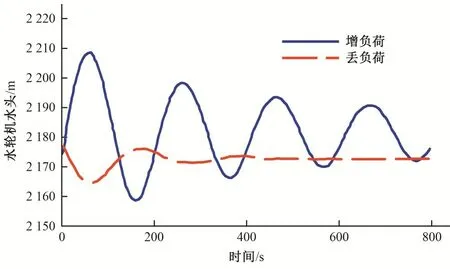
图5 上游最低水位下增负荷和丢负荷调压室水位变化图Fig.5 Water level variation diagram of surge chamber under load increase and loss at the upstream lowest water level

机组增容改造后需要对原电站调节保证设计值以及输水发电系统小波动稳定性进行复核计算，经过数学模型复核计算研究，沙坪电站增容5%后，电站在上游水库最高水位2 187.00 m运行，三台机组丢弃全部额定负荷的情况下，蜗壳最大压力为234.754 m，压力升高23.70%，小于规范要求的30%，也小于电站原设计要求的蜗壳最大压力为243.00 m；机组最大转速升高值发生在水库最低运行水位2181.50 m 三台机组满发运行并同时丢弃负荷的最大转速为640.528 rpm，相对额定转速升高49.45%，小于规范要求的60%；尾水管进口最低压力0.461 m，真空度满足要求，调节保证计算各项指标满足水电站机电设计规范要求，同时输水发电系统小波动也是稳定的，改造后的水轮机调节系统调节品质优良，限于本文篇幅，调保计算和小波动复核内容不做详细介绍，仅给出结论

5 结 论

本文基于沙坪电站的布置形式，根据电站运行记录的资料，运用电站多台机组运行各机组出力计算原理计算现有输水隧洞的糙率值，分析电站的增容能力，得到以下结论。

（1）在稳定工况下，通过数学模型计算的调压室水位和水轮机水头与电站实测值差异很小，计算值和实测值的平均相对偏差小于0.9%，验证了提出的数学模型的准确性。

（2）沙坪电站原有引水系统具备增容5%的能力，但机组引水流量会略有增加，在综合考虑原有基坑尺寸不变的条件下，建议转轮直径由原来的2.03 m 增大至2.10 m，此时3 台机组的总引用流量为112.331 m3/s。

（3）沙坪电站增容改造后的水力过渡过程计算表明，调压井的最高和最低涌浪水位满足仍然满足设计规范要求，调压井运行是安全的；电站调节保证复核计算和输水发电系统小波动复核计算成果也能满足有关设计规范要求。本文提出的水力计算方法可为类似电站的增容改造、机组招标等提供借鉴和参考。