一种加速度辅助“当前”统计模型距离跟踪方法*

蒋兵兵，蔡 猛，祝伟才，马宪超，佘彩云，黄 飞，王 静

（上海无线电设备研究所·上海·201109）

0 引 言

目标跟踪，包括单目标跟踪与多目标跟踪，一直是工程应用中棘手且热门的方向。其应用范围广泛，涉及军事领域的目标预警、制导系统，民用领域的全球定位系统（Global Positioning System，GPS）导航、机器人系统等。

获取运动目标量测数据后，如何利用合适的跟踪模型与跟踪算法完成对目标运动状态或特点的估计，并对其运动进行预测跟踪，是目标跟踪工作的难点。长期以来，学者们着力于解决两类问题：一是建立更优的目标机动跟踪模型，目前常用的跟踪模型均可在文献中找到；二是采用各种机动分析、估计方法以及新理论改进或开发新的跟踪算法。

跟踪算法中状态方程的状态转移矩阵，是目标跟踪模型的直接映射。在目标跟踪技术研究的早期，常速度与常加速度这两个目标运动模型应用广泛。当这两类模型对大机动目标跟踪效果欠佳时，Singer给出目标加速度服从一阶零均值时间相关过程的假设，并提出著名的Singer模型。然而，当目标正以某一加速度机动时，采用零均值模型显然不合理。周宏仁在Singer模型的基础上，提出“当前”统计（“Current” Statistical，CS）模型。该模型假设机动目标加速度的均值为“当前”加速度的预测值，利用实时在线的目标信息，将Singer模型中加速度的非条件概率密度函数替换成修正的瑞利概率密度分布函数。

此后，机动目标跟踪算法的发展进入了繁盛期，提出的算法大致可以分为两类：一类是先检测目标机动状态后再处理，如输入估计技术、变维状态空间方法等；另外一类是用多种模型来描述，如交互多模型（Interactive Multiple Model，IMM）算法、自适应交互多模型算法等。不同类型跟踪模型的组合决定了IMM估计器的有效性。

应用高脉冲重复频率脉冲多普勒（High Pulse Repetition Frequency Pulse Doppler, HPRF-PD）体制的数字阵列雷达，由于高占空比这一特点，容易产生距离遮挡效应。解决这一问题的主流方法是采用多脉冲重复频率机制，其中对脉冲重复频率的切换准则是关键。实际工程中，通常根据相对距离切换合适的脉冲重复频率。因此，得到精确的距离跟踪值能够提升实际应用性能指标。

为获取精确的距离跟踪值，首要的是实现对相对距离的准确测量。雷达发射波形的均方根带宽与距离跟踪通道信号的信噪比决定了距离测量值的精度。当HPRF-PD体制的数字阵列雷达距离通道的信噪比给定后，相应的距离测量精度就确定了。尽管目前雷达系统能够得到的测距精度已经很高，但利用有效的距离跟踪算法，可实现对距离测量值的平滑并减小测距方差，得到更精确的相对距离。因此，提高距离跟踪精度的难点就集中到对状态转移矩阵的精确描述上。

本文首先概述了经典的“当前”统计模型及递归线性平滑牛顿预测器；之后给出了所提的加速度辅助“当前”统计模型算法；最后通过计算机仿真，验证了典型场景下改进距离跟踪方法的有效性。

1 算法基础

1.1 “当前”统计模型

目标跟踪领域主流的目标跟踪模型是IMM算法，但CS模型同样具有可靠的工程应用性能；加之其计算量相较于IMM算法可忽略不计，在对单个目标的跟踪场景中，CS模型也是最常用的方法之一。

目前的研究工作主要集中在CS模型的自适应处理上。进展可分为两类：一是将CS模型与其他模型算法组合后形成新算法，如基于修正强跟踪滤波器的当前统计模型算法和基于概率假设密度的当前统计模型算法等。此类方法通过提升跟踪模型的复杂度以提高跟踪性能，但单纯通过提高模型复杂度的方法并不具有普适性。另一种是针对CS模型本身的局限性所提出的自适应算法，如自适应当前统计模型算法、改进的当前统计模型算法、基于当前统计模型的自适应无迹卡尔曼滤波算法等。相较于第一类算法，此类方法主要针对CS模型中的目标机动频率与目标加速度上下限进行改进。

“当前”统计模型针对的是加速度在一定范围内的机动目标，其模型中目标加速度上下限也由此引入。然而，虽然预设与初值的方法相较于经典CS模型算法的性能更优，但算法并未完全改进。提高CS模型性能的关键点在于实时自适应地计算目标机动频率，同时避免加速度极限值的使用。

CS的数学模型为

（1）

CS模型中对应的过程噪声协方差矩阵为

（2）

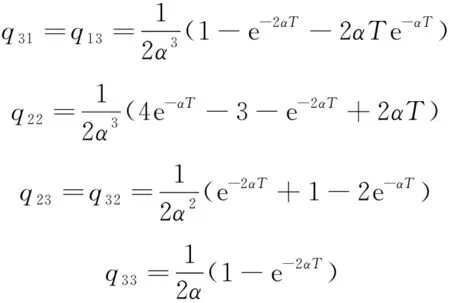
CS模型中，与的预设值是常数。当取小值时，丧失了对机动目标快速响应的能力；反之，当取大值时，其对机动目标的响应速度会提高，但又无法对非机动目标实现精准跟踪。

随着航空技术的高速发展，飞行器的机动能力也越来越先进，有文献针对目标机动加速度变化率采用高度机动目标的Jerk模型。考虑“当前”统计模型中参数的引入原因，可认为其是在缺乏目标加速度测量手段的年代中一种智慧的妥协，但目前更好的做法是规避的使用。

1.2 RLSN概述

递归线性平滑牛顿（Recursive Linear Smoo-thed Newton, RLSN）预测器可实现无延迟估计。量测信号如下

（）=（）+（）

（3）

式中，（）为不含噪声的光滑初始信号；（）为干扰噪声；（）为被控对象的量测输出，即RLSN的输入信号。用阶多项式对初始信号（）建模

（）=+++…+

（4）

式中，为多项式系数，=0,1,…,，为多项式阶数。阶多项式的步向前预测器的域传递函数为

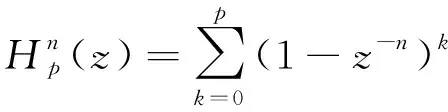
（5）

对式（5）进行平滑操作，得到包含递归方式的线性平滑牛顿预测器传递函数为

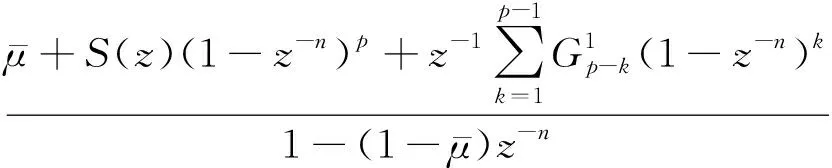
（6）

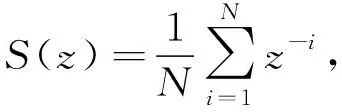
2 改进的距离跟踪算法

在CS模型中引入，实际上是跳过了对径向加速度的测量。对于HPRF-PD体制的雷达系统，采用快速傅里叶变换算法,从窄带回波信号中得到速度测量值。在第个CPI时刻，在准确获取雷达平台与目标之间的径向速度后，考虑到HPRF-PD体制雷达的CPI持续时间短，利用径向速度的历史值及RLSN预测器，可对径向加速度进行估计。采用一阶一步前向预测器，其离散域传输函数为

（7）

其中，为反馈比例因子;为滑动平均器的阶数。预测器的信号流图如图1所示。

图1 一阶一步前向RLSN预测器的信号流图Fig.1 Signal flow chart of first-order first-step forward RLSN predictor

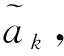
（8）

按照式（8），当帧计数≥+2时可实现加速度的预估。

简化Sage-Husa滤波方法在已知过程噪声协方差矩阵后,可获取自适应量测噪声协方差矩阵。一般地，在参数估计中，通常用遗忘因子增大对最近数据的权重系数。简化的Sage-Husa估计器用式（9）计算。

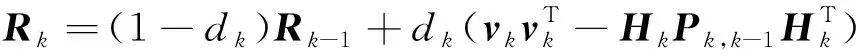
（9）

=

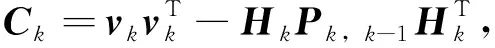
（10）

配合简化的Sage-Husa估计器后，得到了改进的距离估计算法。其实现了对与的同时自适应计算，表现出更好的普适性。

改写“当前”统计模型表达式

（11）

其中，（）表示测得的径向加速度。

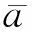
对比式（1）与式（11），可知

（12）

对式（12）两边分别求导数，有

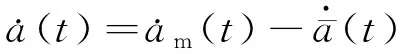
（13）

将式（13）代入式（11）中的第二个等式，得

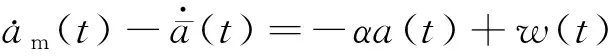
（14）

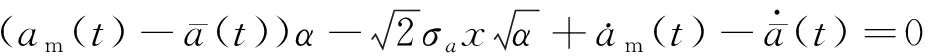
（15）

由此求解，得

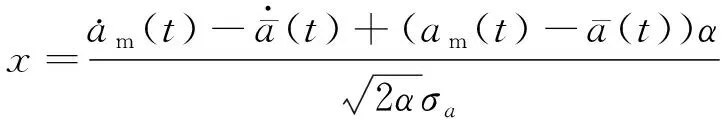
（16）

限定的范围，并假设：∈[ -,],其中∈N。

上述假设成立的概率为落入[-,]这个区间的概率。考虑到服从标准正态分布，则当≥4时，此假设成立的概率至少为99.994%。本文在此处作近似，认为当≥4时，∈[-,]。

基于上述假设，有

（17）

其中，≥4。

经分类讨论后，可得：

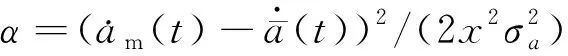
（18）

=

（19）

选择满足相应条件时的解作为的值。若存在2个正根，则选择较小的根作为的值；无解时，保持的值不变。

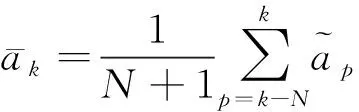
（20）

（21）

加速度估计环路中的滑动平均器阶数及比例因子对加速度估计精度的影响较大。一般来说，阶数越高，加速度估计精度越高，但会导致加速度估计环路启动帧越靠后；比例因子越低，加速度估计精度越高，但估计环路的记忆性越强，即估计值对历史加速度估计值的依赖性越强。故需合理配置滑动平均器阶数及比例因子。

获取加速度估计值后，本文给出了目标机动频率的解析解，机动频率估计精度与加速度估计精度高度相关。因此，在保证加速度估计环路启动时效性、估计环路对最新数据依赖性的基础上，需合理提高滑动平均器阶数和比例因子，从而有效提升机动频率的估计精度。

3 计算机仿真

在大地坐标系中，以系统零时刻目标的位置作为坐标系原点′，雷达指向目标作为′轴正方向，在′′′坐标系下（′′轴位于包含有′′的铅垂面内,且′′到′′为顺时针方向，′′轴与′′、′′构成右手坐标系）。雷达沿着′′正向以=300m/s的速度匀速运动，目标沿着′轴负方向以=200m/s的速度匀速向着雷达飞行，在′′′、′′′平面内分别做正弦运动，两者的空间运动轨迹如图2所示，雷达与目标之间的距离从7.8km变化到4.5km。

图2 仿真场景图 Fig.2 Simulation scene schematic diagram

图3对比了本文提出的加速度辅助CS（Acceleration Aided-CS，AA-CS）算法与经典的CS模型在仿真场景中得到的距离跟踪误差。AA-CS算法的跟踪性能优于经典CS模型算法，其跟踪误差下降速率更快，也佐证了需要为量测噪声协方差矩阵做自适应计算的重要性。此外，AA-CS算法的距离跟踪误差方差也更小，如图4所示。图5所示为AA-CS算法中的量测噪声协方差值。可以看出，在几个CPI后很快达到了稳定的收敛状态。

图3 距离跟踪误差对比曲线Fig.3 Range tracking error comparison

图4 距离跟踪误差方差对比曲线Fig.4 Range tracking variance comparison

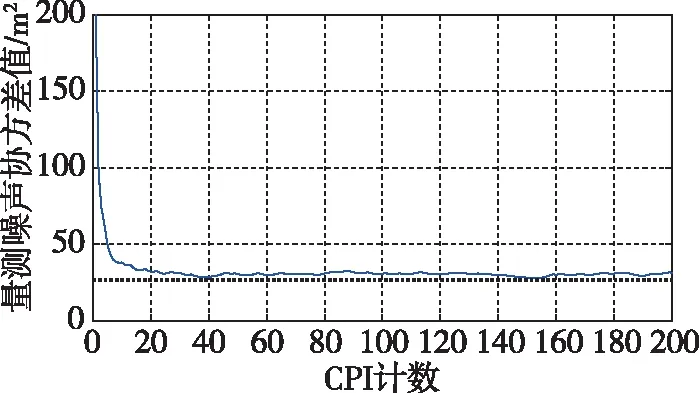
图5 AA-CS的量测噪声协方差曲线Fig.5 Measuring noise covariance value in AA-CS

4 结 论

本文通过一阶一步迭代线性平滑牛顿预测器，实现了对当前帧目标径向加速度的预估，得到了“当前”统计模型中目标机动频率值的解析解，无需设置模型中目标机动加速度极限值，即可实现过程噪声协方差矩阵的自适应计算；并利用简化的Sage-Husa滤波器改进了“当前”统计模型，实现了量测噪声协方差矩阵的自适应更新，有效地拓宽了“当前”统计模型跟踪算法的使用范围，进一步增强了实际工程中的应用价值。