基于残差网络的航空发动机滚动轴承故障多任务诊断方法

康玉祥，陈 果，尉询楷，潘文平，王 浩

(1.南京航空航天大学 民航学院，南京 210016；2.南京航空航天大学 通用航空与飞行学院，江苏 溧阳 213300；3.北京航空工程技术研究中心，北京 100076)

当前，以航空发动机为代表的的旋转机械，通常运行在高负荷、高转速等恶劣的环境之下，导致滚动轴承故障频发，轻则系统失效，造成经济损失，重则机毁人亡，严重威胁飞行安全。然而，由于航空发动机滚动轴承早期故障特征非常微弱，很难实现故障的精确诊断，因此，研究高效的滚动轴承智能故障诊断与检测技术对确保航空发动机安全运行有极其重要的意义[1-2]。

传统的基于信号分析和机器学习的故障诊断方法，首先采用小波分析、傅里叶变换等技术从原始振动信号中提取故障特征。然后，以所提取的一维故障特征为输入，利用支持向量机(support vector machine,SVM)、和神经网络(neural networks,NN)等机器学习模型实现故障诊断[3]。这类方法的诊断结果严重依赖于特征提取的有效性和机器学习模型的精度，使得模型泛化能力较差。

目前，深度学习在滚动轴承故障诊断中得到了普遍的应用和广泛的认可，与传统机器学习方法相比，深度学习方法有两个突出优势，一是可以从原始数据中直接进行特征学习，并且所学特征的判别能力远超手工提取的特征；二是可以实现端到端的学习，即可以直接学习从原始数据到类别标签的映射。Lei等对当前基于人工智能方法的故障诊断研究现状进行了综述，阐述了深度学习在故障诊断中的应用流程，并指明了未来基于深度学习的故障诊断方法的研究路线。田科位等[4]通过将注意力机制的挤压与激励结构引入到残差神经网络，提出了一种改进的深度残差网络模型，用于滚动轴承故障诊断，验证结果表明所提模型在变工况条件下具有很好的诊断效果。Zhou[5]针对故障样本数据不平衡的问题，提出了一种新的生成对抗网络(generative adversarial networks,GAN)用于故障样本的生成，然后基于生成的故障样本和实际的样本进行故障诊断，结果表明该GAN具有很强的故障识别能力。孟宗等[6]提出一种基于二次数据增强和深度卷积的模型，用于少故障样本情况的诊断，取得了很好的效果。王琦等[7]通过引入引入1×1卷积核、改进全连接层等技术，提出一种基于改进一维卷积神经网络的滚动轴承故障识别方法，验证结果表明，该方法具有计算速度快，诊断精度高的优点。刘飞等[8]提出了一种基于迁移学习与深度残差网络的快速故障诊断算法，该方法具有训练时间短、诊断精度高的优点。实现了高精度的滚动轴承故障诊断。此外，诸如长短期记忆网络(long short-term memory,LSTM)、深度置信网络(deep belief network,DBN)等方法也开始应用于滚动轴承故障诊断，Lei等[9]采用LSTM精确诊断了风电机组轴承的故障类别。Shao等[10]对深度信念网络进行了改进，同时将改进模型用于滚动轴承的故障诊断中，并验证了模型的有效性。在损伤大小预测方面，Nguyen等[11]利用深度神经网络(deep neural network,DNN)准确预测了轴承在不同裂纹尺寸条件下性能退化程度。王震等[12]提出了一种用于故障分类与损伤尺寸预测的多任务深度学习模型，并取得了较好的效果。然而，该模型并未对在增加噪声和对未参与网络训练的损伤尺寸预测情况进行考量。综上，针对滚动轴承的智能诊断方法主要存在如下可改进之处：①当前基于深度学习的滚动轴承故障诊断技术通过将不同损伤尺寸作为多种故障模式进行分类识别，而忽略了损伤尺寸的连续性，且不能同时实现故障的状态识别、定位分析与损伤尺寸的定量预测，从而无法判断故障的严重程度；②上述大多数深度学习方法任务单一，不能有效利用网络层的参数，造成算法训练后的信息冗余。

鉴于此，本文采用能够有效避免梯度消失的深度残差网络，建立能够同时进行故障状态识别、故障部位识别、以及故障程度识别的并行多任务模型。并利用实际滚动轴承故障模拟试验数据进行方法验证。

1 多任务残差网络

1.1 残差结构块

2015年He等[13-14]针对深度神经网络在训练过程由于出现梯度消失而导致的网络性能退化的问题，提出了深度残差网络(residual networks，Resnet) 。Resnet在卷积神经网络的基础上增加了残差结构块，理论上这种结构块可以使得网络深度在硬件条件允许的前提下无限的增加，而不出现性能退化现象。残差结构块如图1所示。

图1 残差结构块Fig.1 Residual unit

图1中输入x在经过卷积、批归一化、激活函数等变换后得到映射函数f(x)，同时，x经过恒等映射(使得变换后的图像和由f(x)获得的图像具有相同的尺寸)后和f(x)进行累加操作得到输出h(x)。图1中:n×n×M1、n×n×M2是M1、M2个n×n大小的卷积核；BN批归一化操作；Relu为激活函数，其具体函数形式如式(1)所示

(1)

1.2 多任务残差网络模型

根据残差网络理论，建立基于残差网络的深层特征提取与共享主框架，在此基础上建立故障状态、部位分类与损伤大小预测的多任务模型。网络具体模型如图2所示。

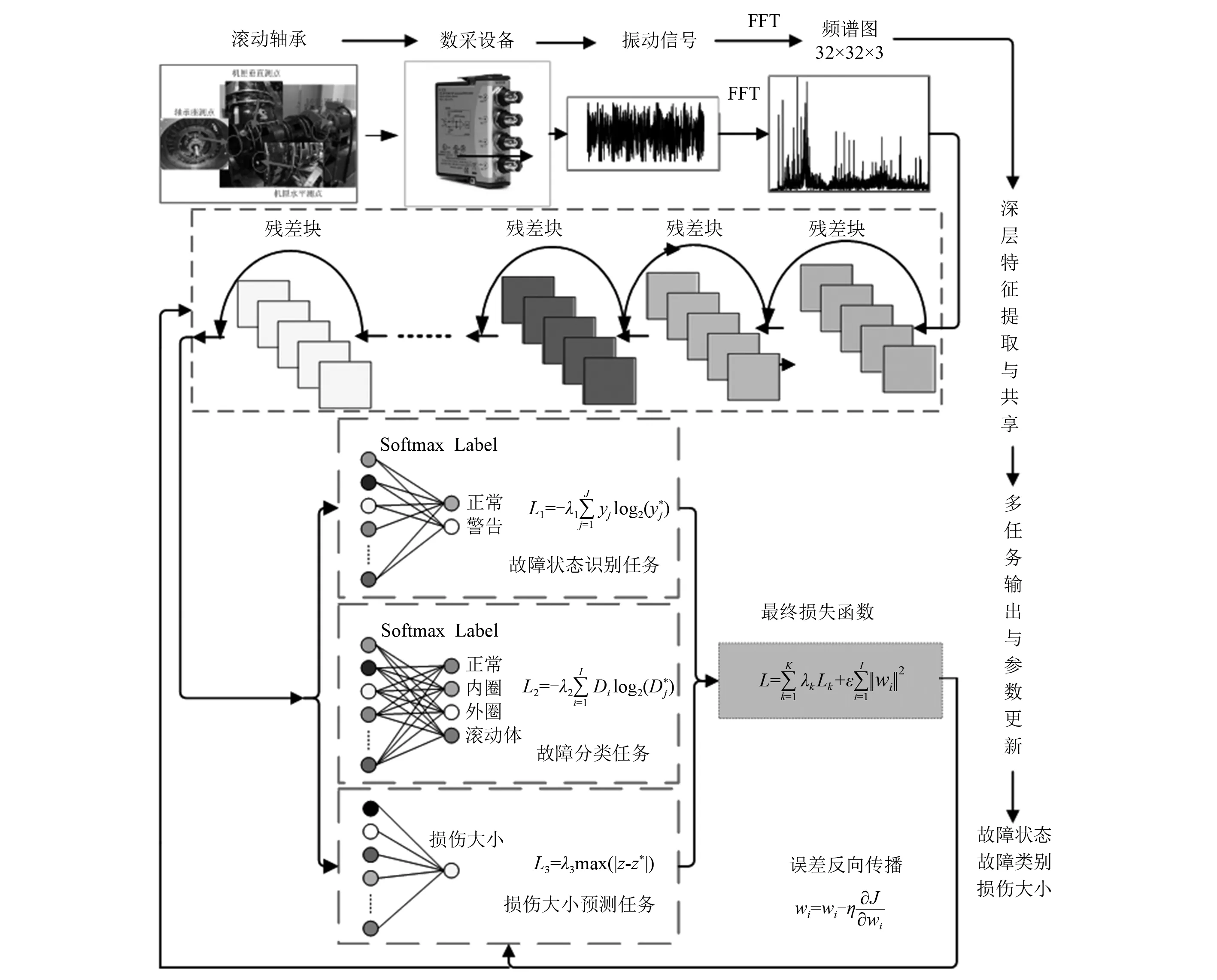
图2 网络模型结构Fig.2 Network model structure

图2所示的多任务残差网络模型主要流程为：

步骤1首先根据数采设备采集得到滚动轴承的振动加速度实时数据。

步骤2采用FFT算法，将振动加速度信号转换为频谱图，并直接保存为32×32×3的图像数据文件。

步骤3以所获得的频谱图文件为多任务残差网络的输入，通过多个残差块进行特征提取。

步骤4将所提取的特征结果分别输入故障状态识别、故障部位诊断任务模块和损伤大小预测任务模块，同时计算各个任务的损失大小Lk。

步骤5根据各个子任务的损失计算联合损失L。

步骤6基于误差反向传播算法进行参数更新。

步骤7保存模型，并同时输出故障类别和损伤大小尺寸信息。

图2中的深层特征提取与共享主框架中由多个残差块串联组成。根据图1中单个残差块的结构信息，很容易得到多个残差块串联后的数学模型如式(2)所示

(2)

根据反向传播算法[15]及文献[16]，可得网络的梯度如式(3)所示

(3)

图2中的故障状态识别任务设计为一层全连接层，应用Softmax函数输出2类故障，分别是正常、故障。故障部位诊断任务设计为一层全连接层，应用Softmax函数输出4类故障，分别是正常、内圈故障、外圈故障、滚动体故障。损伤大小预测任务为回归预测，输出为连续的损伤尺寸值。

本文损失函数采用联合损失函数，如式(4)所示

(4)

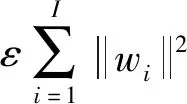
文中L1为故障状态识别损失值，采用交叉损失函数如式(5)所示

(5)

文中L2为故障分类任务损失值，采用交叉损失函数如式(6)所示

(6)

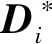
L3为损伤尺寸预测损失值，采用绝对误差损失，如式(7)所示

L3=λ3max(|z-z*|)

(7)

式中:z为实际损伤尺寸；z*为预测输出值。

1.3 数据预处理

由于采样频率一般都大于10 K，当取1 s的振动加速度信号经过FFT所得的频率值较多。而直接将所得的频谱存储为32×32大小的图像后会产生数据失真现象，导致有用的频率信息消失，为保证所得图像数据在存储后不失真，首先计算了滚动轴承的故障特征频率，以5倍故障特征频率的范围做频谱图，以该频谱图作为网络输入。

1.3.1 滚动轴承故障特征频率

滚动轴承节径D、接触角α、滚珠直径d、滚珠数Z以及内外圈相对转速共同决定了滚动轴承故障特征频率。对于外圈固定，内圈转动的滚动球轴承，设转速频率fr，则滚珠公转频率或轴承保持架频率fc、滚珠自转频率fb、轴承外圈频率fout、轴承内圈频率fin如式(8)所示

(8)

本文采用美国凯斯西储大学的滚动轴承故障模拟试验数据集和南京航空航天大学的滚动轴承故障模拟试验数据集，轴承信息分别如表1和表2所示。

表1 美国西储大学数据集滚动轴承信息Tab.1 Rolling bearing information from Western Reserve University dataset

表2 南京航空航天大学数据集滚动轴承信息Tab.2 Data set of rolling bearing information of Nanjing University of Aeronautics and Astronautics

根据式(7)和两种故障诊断数据集的最大转速，计算各个滚动轴承故障特征频率如表3所示。

表3 轴承故障特征频率Tab.3 Bearing fault characteristic frequency

在数据集划分方面，首先，将原始的振动加速度信号按照7∶3的比例划分为训练集和测试集。对于训练集按照数据采样频率，采用数据增强方法，以一定的间隔步长对时域振动信号进行采样，如图3所示，其中步长为1 000个点，样本数为1 s内的采样点数。然后，对每组样本点进行FFT，取5倍故障特征频率范围内的频谱图，将获得的频谱图直接保持为png格式的图形文件，图形文件大小为32×32×3，如图4为转换后的频谱图。

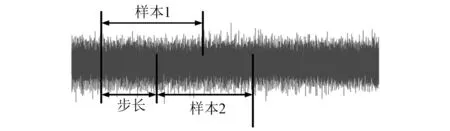
图3 振动信号采样Fig.3 Vibration signal sampling

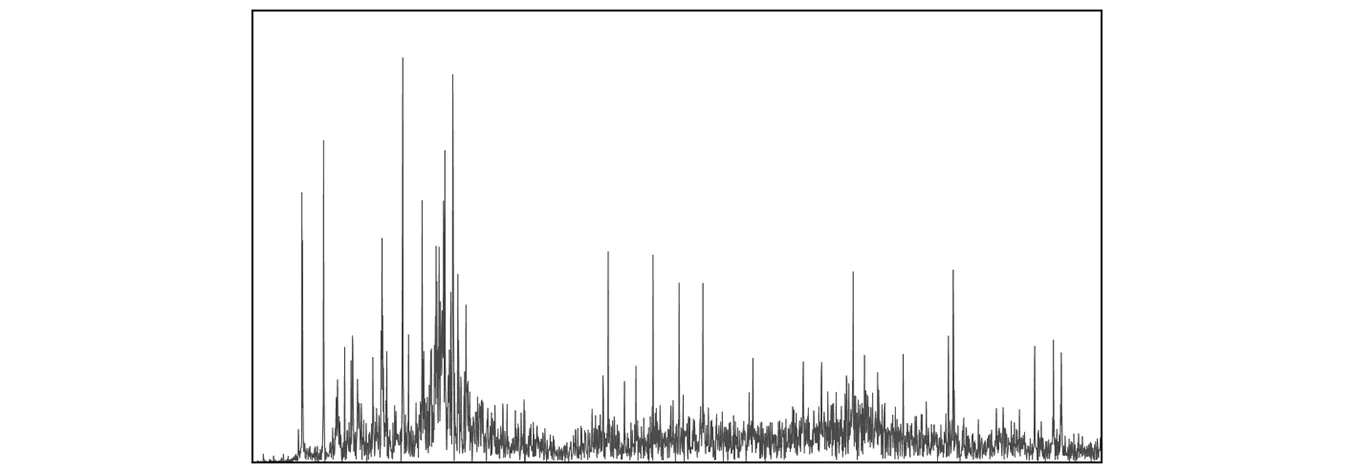
图4 轴承信号的频谱图Fig.4 Spectrum diagram of bearing signal

1.3.2 标签平滑化

采用one-hot编码进行梯度损失计算时，只考虑了正确标签，而忽略了错误标签的损失，致使模型在训练集上有很好的效果，在测试集上却表现平平。为了解决这种泛化能力不足的问题，本文采用如式(9)所示的标签平滑技术对标签进行平滑处理

y′j=(1-η)yj+ημ

(9)

式中：yj为原始one-hot编码后的标签，包括故障状态标签、故障部位标签；y′j为经过平滑后的标签;η为平滑因子;μ为随机噪声。

2 滚动轴承故障诊断试验

为了验证本文算法在滚动轴承故障诊断与损伤大小识别中的有效性。首先，选择了研究者普遍采用的美国凯斯西储大学的滚动轴承故障诊断数据集[17]进行验证。其次，应用于南京航空航天大学的带机匣的航空发动机转子试验器滚动轴承故障试验数据的诊断，并进行多种方法的对比验证。

2.1 美国凯斯西储大学滚动轴承模拟故障试验数据诊断

选择美国凯斯西储大学滚动轴承故障诊断数据集的驱动端数据，其相应的轴承型号为SKF6205，选择数据采样频率为12 kHz。轴承共有内圈、外圈、滚动体三种加工缺陷故障状态和正常状态，共四种状态，其中加工缺陷故障状态分别包含0.177 8 mm，0.355 6 mm，0.533 4 mm，0.711 2 mm四种损伤尺寸。为了验证算法不受负载、转速等工况的影响。试验数据集包含了各种不同条件下的滚动轴承故障数据。采用1.3节中的数据预处理方式后，数据集所包含的样本信息如表4所示。

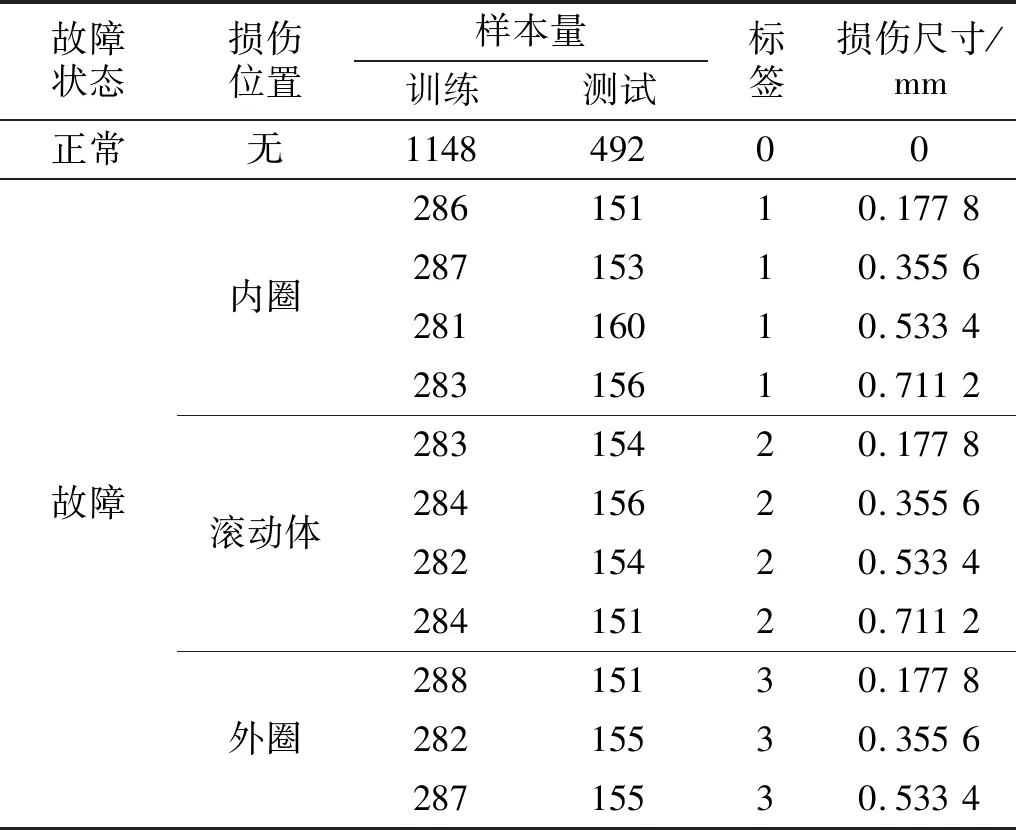
表4 数据集样本信息Tab.4 Sample information of the data set

2.1.1 网络参数

本文试验中采用GPU为NVIDIA GTX1660 6 G;i5-9600K 处理器；8 G内存；运行系统为Windows10；编程语言为python3.7；深度学习框架为Tensorflow1.15.设置批处理样本量为64；迭代轮数为100；采用的优化算法为Adam算法,学习率为0.000 1。本文模型参数如表5所示。

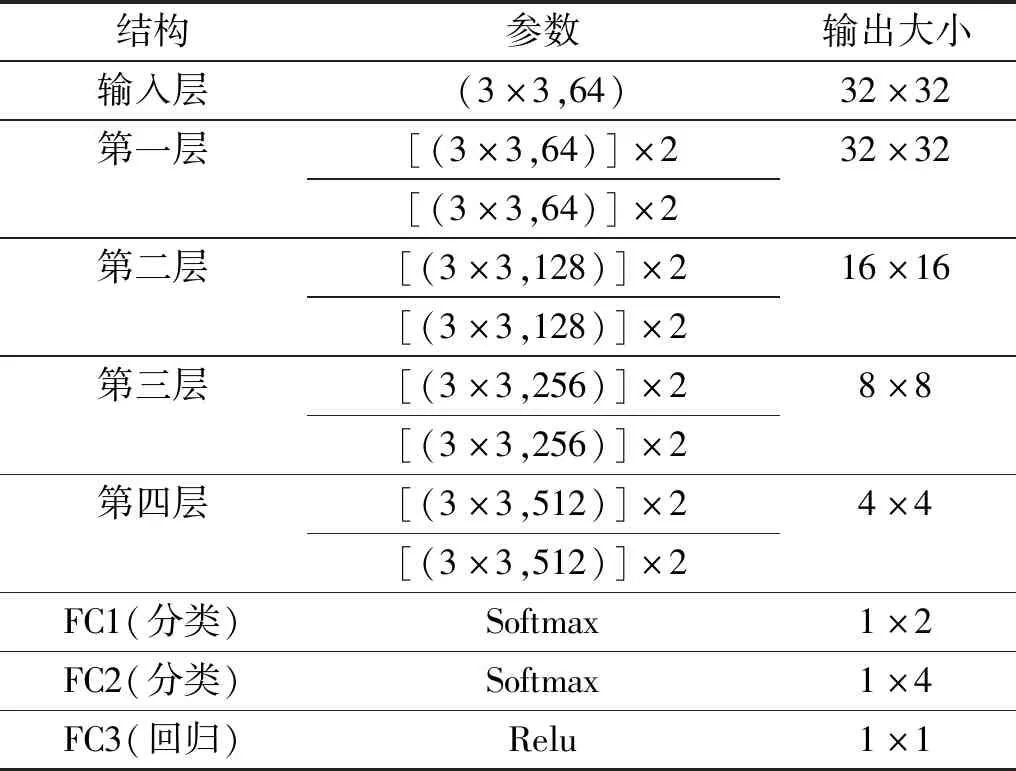
表5 深度残差对冲网络信息Tab.5 Information of the Resnet

多任务网络中采用分类准确率来表征故障诊断结果，采用所有预测样本的最大绝对误差的绝对值来反映损伤尺寸的预测精度，如式(10)所示

(10)

多任务中各个任务的惩罚因子λk对最终的测试结果有很大的影响，因此，将λk设置为残差网络的学习参数，让网络能够进行自我学习获得最优的参数组合。采用如式(11)所示的方式对网络性能进行评价。

式中：ψ为评价结果，ψ→0说明预测效果越好；op为故障状态预测正确的个数；O为故障状态预测的样本数量;np为故障分类正确的个数；N为故障类别的样本数量。采用交叉验证的方式，经过多次测试后参数λ1,λ2,λ3在λ1=0.2,λ2=0.1,λ3=0.4的时候ψ=0.003 5达到最小值。因此，以下测试结果均基于上述参数进行。

2.1.2 测试结果

根据2.1.1节中的残差网络层数及相应参数搭建网络，并对网络进行测试。如图5所示为通过交叉验证的方式获得的损伤尺寸预测精度δ和本文自定义的网络性能评价指标ψ的变化曲线。在迭代100次之后损伤大小的测试结果趋于稳定，最后达到0.003 5 mm的预测误差。网络性能评价指标ψ在最后收敛趋于0.003 5，说明分类诊断精度达到100%、损伤尺寸预测误差均趋于0.003 5 mm。

图5 诊断结果变化曲线Fig.5 Diagnostic outcome

如图6所示为损伤尺寸预测结果。图中结果也显示所提多任务模型具有较高的损伤测试精度。

图6 损伤尺寸预测结果Fig.6 Damage size prediction results

为进一步说明算法的优势，选择经典的卷积神经网络(convolutional neural networks,CNN)(引用文献)、深度神经网络算法，通过将这两种算法改进为多任务网络后和本文的多任务残差网络进行对比。试验中每种方法都进行10次计算，取最终的算法平均结果。对比结果如表6所示。

表6 网络诊断结果Tab.6 Network diagnostic results

表6中的结果说明，相比其他两种多任务残差网络模型，本文的多任务残差网络模型在分类精度和损伤大小识别中均高于其他算法。尤其是在损伤大小预测方面，本文的最大绝对误差绝对值δ=0.003 5，而其他算法中最好的结果也仅为0.034 5，约为本文算法的10倍，充分证明了本文算法的优越性。

2.2 南京航空航天大学带机匣的航空发动机转子模拟试验器故障试验数据诊断

本试验用到的试验设备包括带机匣的航空发动机转子模拟试验器、AI002加速度传感器、JM5937动态信号测试分析系统等。带机匣的航空发动机转子模拟试验器及相应的加速度传感器安装位置如图7所示，该试验平台是以1∶3比例仿制的某型真实发动机。试验平台能有效的反映航空发动机振动信号在传递过程中的衰减特性。试验共使用了9个HRB 6206深沟球轴承，采用电火花线切割技术，人为在其外圈及内圈表面分别加工了四种不同宽度的凹槽来模拟不同故障尺寸，凹槽宽度依次为1.0 mm，1.4 mm，1.8 mm和2.2 mm，故障加工细节如图8所示。试验时依次装入9个轴承，利用安装在试验器轴承座、机匣垂直上方和水平方向上的3个加速度传感器采集振动信号，每种故障中设置试验器转速分别为：1 000 r/min，1 500 r/min，2 500 r/min，3 000 r/min。采样频率设置为32 kHz。为能够真实的反应振动信号在航空发动机上的传递衰变特性，验证本文方法用于航空发动机滚动轴承诊断中的有效性，本文选择安装与机匣上的垂直加速度测点进行诊断分析。

图7 航空发动机试验器Fig.7 Acro-engine rotor tester

图8 轴承故障加工细节Fig.8 Processing details of bearing fault

如图9所示为在测试数据上的损失和ψ的变化曲线。图中曲线可以很容易的看出随着训练次数的增加，模型的损失值变小，最后收敛于0值。针对本文所提多任务模型评价系数ψ的变化曲线，ψ值最终也同样收敛于0值，这也很好的的反应出本文多任务测试结果的准确性，即：在故障诊断分类任务中能准确的识别出故障类型；在损伤大小识别任务中能很好的对损伤大小进行预测。

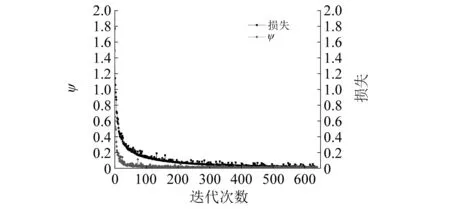
图9 训练目标参数变化曲线Fig.9 Training target parameter change curve

为较好的反应本文损伤大小预测结果具有较高的精度，如图10所示为损伤尺寸预测结果，图中结果同样反映了本文针对损伤大小识别结果的准确性。

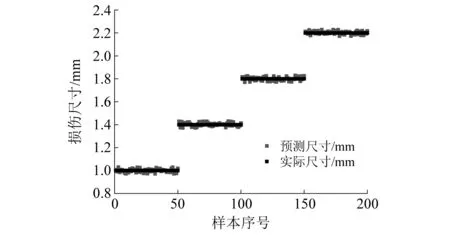
图10 损伤尺寸预测结果Fig.10 Fault size prediction results

在经过10次试验取均值后和CNN、DNN算法进行比较，各个任务10次的计算结果分别如图11、图12、图13所示，最终结果如表7所示。

图11 故障状态诊断结果Fig.11 Fault state diagnosis results

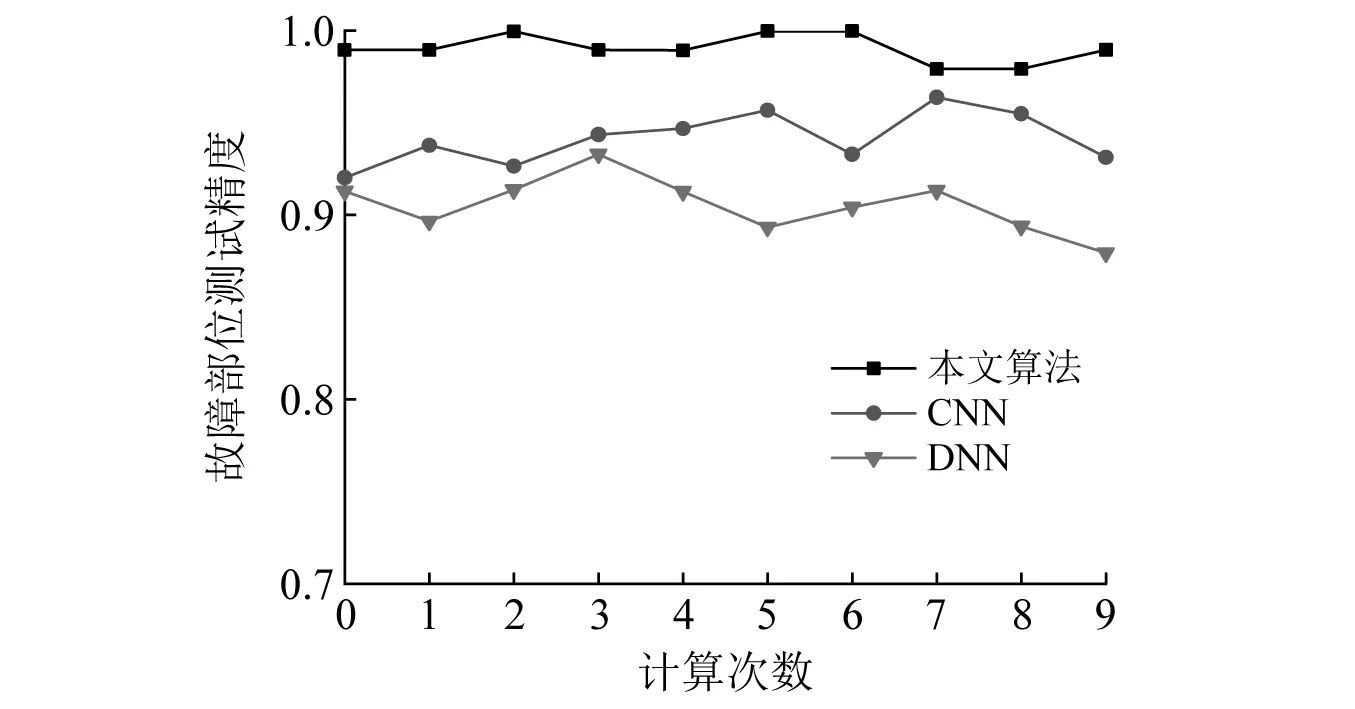
图12 故障部位诊断结果Fig.12 Fault location diagnosis results

图13 故障尺寸预测结果Fig.13 Fault size prediction results

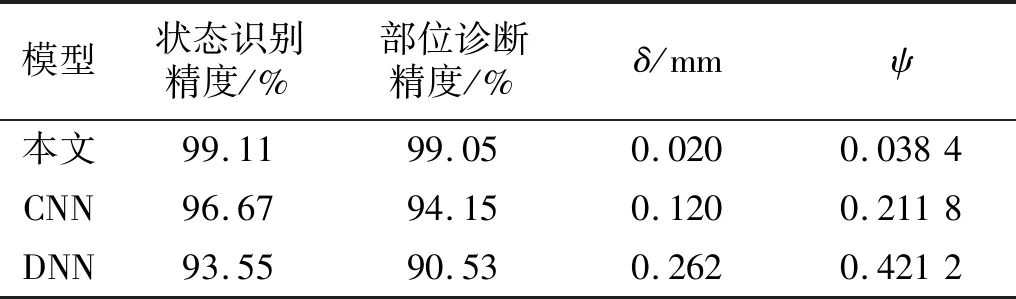
表7 网络诊断结果Tab.7 Network diagnostic results

表7中结果显示，传统DNN算法，状态识别精度为93.55%，部位诊断精度为90.53%，δ=0.262 mm。测试效果相对较好的是CNN，其分类精度为96.67%，δ=0.120 mm。测试效果最好的是本文的多任务残差网络，分类精度为99.11%，部位诊断进度为99.05%，δ=0.020 mm，相比CNN，状态识别和部位诊断精度分别提高约3%和5%的同时，损失大小预测效果提高了6倍左右。以上测试结果充分说明本文算法在进行多任务学习中的有效性。

2.3 模型泛化性能测试

2.3.1 对未参与训练的故障尺寸进行预测

为进一步说明本文算法的强泛化性能，针对南京航空航天大学滚动轴承试验数据集，选择内圈和外圈两种故障类型，其中，训练集中包含内圈1.0 mm，1.4 mm，2.2 mm的损伤尺寸，外圈1.0 mm，1.8 mm，2.2 mm的损伤尺寸。内圈选择1.8 mm的损伤尺寸为测试集，外圈选择1.4 mm的损伤尺寸为测试集。在2.2节模型训练的基础上，采用迁移学习的技术，重新对模型进行训练。

如表8所示为模型对未参与训练的样本进行预测后的故障状态识别、故障部位诊断以及故障尺寸大小预测结果。表8中的结果显示，对于未参与训练的故障尺寸样本，故障状态识别精度和故障部位诊断精度相比2.2节中的结果均有所降低，其中，故障状态识别精度降低5.08%为94.03%、故障部位诊断精度降低4.54%为94.51%。对于故障尺寸大小预测任务，预测结果误差为0.356 7 mm，相比表7中的结果，尺寸预测误差有所增加，因所预测的损伤尺寸未参与网络的训练，预测结果应该介于某两个参与训练的尺寸中间。而另外两种算法在故障状态识别、故障部位诊断中精度降低幅度均达到了5%，尺寸大小预测误差均有所增加。对比三种算法，仍可得出本文算法具有更强泛化性能的特点。

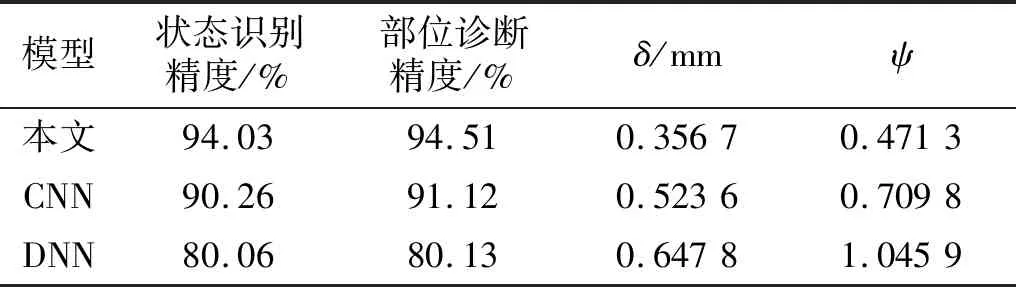
表8 网络测试结果Tab.8 Network test results

如图14所示为未参与训练的内圈故障尺寸预测结果图。图中结果可以看出，对于未参与训练的1.8 mm损伤尺寸，本文算法的预测结果介于1.4～2.2 mm。测试结果证明网络能够准确提取故障特征，并对损伤尺寸进行精确预测。

图14 内圈故障尺寸预测结果Fig.14 Inner ring fault size prediction results

如图15所示为未参与训练的外圈故障尺寸预测结果图。图中结果可以看出，对于未参与训练的1.4 mm的损伤尺寸，预测结果介于1.0～1.8 mm。测试结果证明网络能够准确提取故障特征，并对损伤尺寸进行精确预测。

图15 外圈故障尺寸预测结果Fig.15 Outer ring fault size prediction results

为进一步说明本文所提算法具有较高的损伤尺寸回归预测精度，对内圈和外圈的预测结果进行统计分析。对于z=1.8 mm的损伤尺寸，分别统计预测结果为1.8±0.1 mm，1.8±0.2 mm，1.8±0.3 mm，1.8±0.4 mm的样本数量，对于z=1.4 mm的损伤尺寸，分别统计预测结果为1.4±0.1 mm，1.4±0.2 mm，1.4±0.3 mm，1.4±0.4 mm的样本数量。同时计算各个范围内的样本量和总样本量的比例关系。统计结果如表9所示。结果显示，对于内圈损伤尺寸z=1.8 mm的情况，预测误差为0.1 mm，0.2 mm，0.3 mm的样本量占比分别为50.67%，77.65%，88.85%；外圈损伤尺寸z=1.4 mm，预测误差为0.1 mm，0.2 mm，0.3 mm的样本量占比分别为85.23%，94.36%，98.10%。以上统计结果表明本文模型的损伤尺寸预测结果较为集中，也进一步验证了模型的泛化性能。

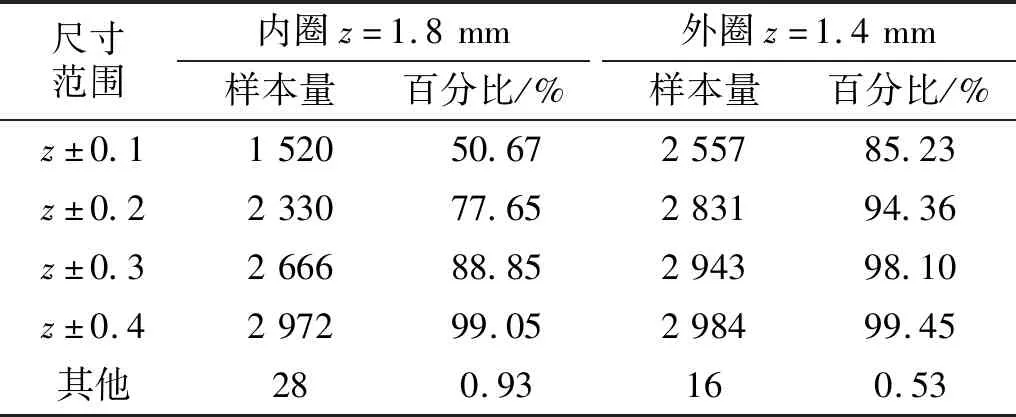
表9 损伤尺寸预测结果统计Tab.9 Statistics of damage size prediction results

2.3.2 噪声对网络性能的影响

对上述未参与训练的损伤尺寸原始振动加速度数据添加均值为0，方差为1的高斯噪声，在对该数据进行预处理后，将其作为模型的输入，用于进一步验证算法的泛化性能。

分别采用三种多任务网络模型，对添加噪声后的数据进行诊断。诊断结果如表10和图16、图17所示。

表10 添加噪声后网络测试结果Tab.10 Network test results after adding noise

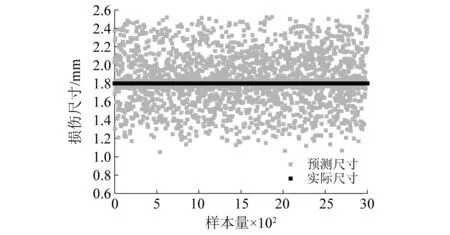
图16 添加噪声后内圈损伤尺寸预测结果Fig.16 Prediction results of inner ring damage size after adding noise

图17 添加噪声后外圈损伤尺寸预测结果Fig.17 Prediction results of outer ring damage size after adding noise

添加噪声后的诊断精度和损伤尺寸预测精度均有所降低。其中本文模型的状态识别精度和部位诊断精度均降低2%左右，损伤尺寸误差增加0.07 mm左右。其他两种算法的诊断精度降幅达8%以上，损伤尺寸预测误差增加0.15 mm以上。说明本文算法相比其他两种算法的泛化性能更高。

以上针对未参与训练的损伤尺寸样本的故障诊断结果说明，本文所提多任务诊断模型能够对未参与训练的损伤尺寸样本进行准确的诊断，且损伤大小预测误差仍具有较高的精度。说明本文所提模型具有较好的泛化性能。

3 结 论

提出了一种基于多任务残差网络的滚动轴承故障状态、部位诊断与损伤大小识别模型，并详细介绍了模型的计算流程和相应的损失函数计算方法等模型细节以及数据集的构建方式。在将本文算法应用于轴承故障诊断的过程中，直接以FFT所得的png频谱图为输入，避免了人为设计输入数据的过程。在西储大学滚动轴承数据集和南京航空航天大学滚动轴承故障试验数据集上的测试结果表明，本文所提算法均展现了同时对故障状态识别、故障部位诊断与损伤大小识别的优势。结果表明本文所提的多任务模型具有较高的诊断精度与损伤大小预测能力，且模型具有很好的泛化性能，也表明该网络具有较好的应用前景。