组合激励下冷轧机工作辊水平振动特性研究

李 丽，郝宇超，李 震

(1.北京科技大学 机械工程学院，北京 100083；2.内蒙古科技大学 机械工程学院，内蒙古 包头 014010)

板带轧机工作过程中普遍存在着明显振动现象。在轧机多种振动形态中，存在着复杂机电液耦合振动问题[1-3]。其中机械结构振动方向的研究重点集中在轧机垂振、扭振、水平振动以及相互耦合等振动问题[4-7]。

毛君等[8]为对轧机振动进行精确的分析，建立轧机六自由度的垂直振动模型，对系统的固有频率和主振型进行分析得到第五阶固有频率是引起自激振动的主要频率。魏静静等[9]为分析波纹辊轧机振动问题，建立四自由度垂振模型，通过有限元仿真发现在垂直方向振动较为明显。和东平等[10]考虑波纹辊轧机界面的非线性因素，建立了两自由度垂直非线性激励模型，为抑制轧机振动提供了理论指导。米凯夫等[11]基于小波分析和分形理论，为准确监视轧机振动提供了有效的识别方法。吴继民等[12]考虑到轧机会受到电磁力矩和轧制力矩双动力源的作用，建立了双自由度的轧机传动等效力学模型，通过复小波变换对非线性参数进行辨识，提出来抑制轧机振动的有效方法。有关学者[13-14]提出一种新的主动振动抑制方法，利用扰动估计和补偿算法设计了基于扩张状态观测器的主动减振器。高崇一等[15]建立了轧机主传动系统与带钢的耦合振动模型，将带钢简化为Euler梁，分析了扭振基频对带钢振动的影响。侯东晓等[16]通过分析辊系垂直位移与扭转振动角对动态轧制力和力矩的影响建立了非线性垂直-扭转振动力学模型。为研究单架机架以及多架机架之间的颤振，王桥医等[17-18]结合辊系多模态结构模型建立了辊系垂直及水平方向的多模态模型以及机架之间的耦合模型。Lu等[19]对轧制过程轧机在垂直-水平-扭转的动态耦合、非线性、多辊平衡等因素进行分析，得出振动系统的分叉点存在性和分叉特点。张阳等[20]综合轧机系统垂直、水平方向的刚性振动和轧辊轴向弯曲变形建立了刚柔耦合动力学模型，得出轧辊模态振型的解析解，为提高轧制精度提供理论依据。

本文以某冷轧机工作辊为研究对象，建立了外激励由频率不等的三个部分组成的非线性动力学模型。分析三种外激励频率在接近系统固有频率时，系统各参数对振动的影响，建立了相应的动力学方程，分析了工作辊在水平方向的振动特性，为研究轧机水平振动提供了合理的理论依据。

1 建立轧机辊系非线性动力学模型

板带轧制是一个复杂的工作过程。为研究冷轧机工作辊机械结构水平方向的非线性振动特性，建立轧机工作辊机械结构非线性模型如图1所示。板带轧制过程中存在复杂的轧制界面，辊缝的非稳态润滑会产生复杂的摩擦力Ff。在辊系机械结构中，工作辊与支撑辊之间会存在一定的偏移距，使液压缸通过支撑辊传递给工作辊的压下力Fp产生一个水平方向的分力。又由于万向接轴的存在，主传动方向会有附加弯矩和摩擦弯矩的产生，其水平方向投影之和为附加水平弯矩，在工作辊轴径位置会产生附加水平力Fws引起轧机的振动。

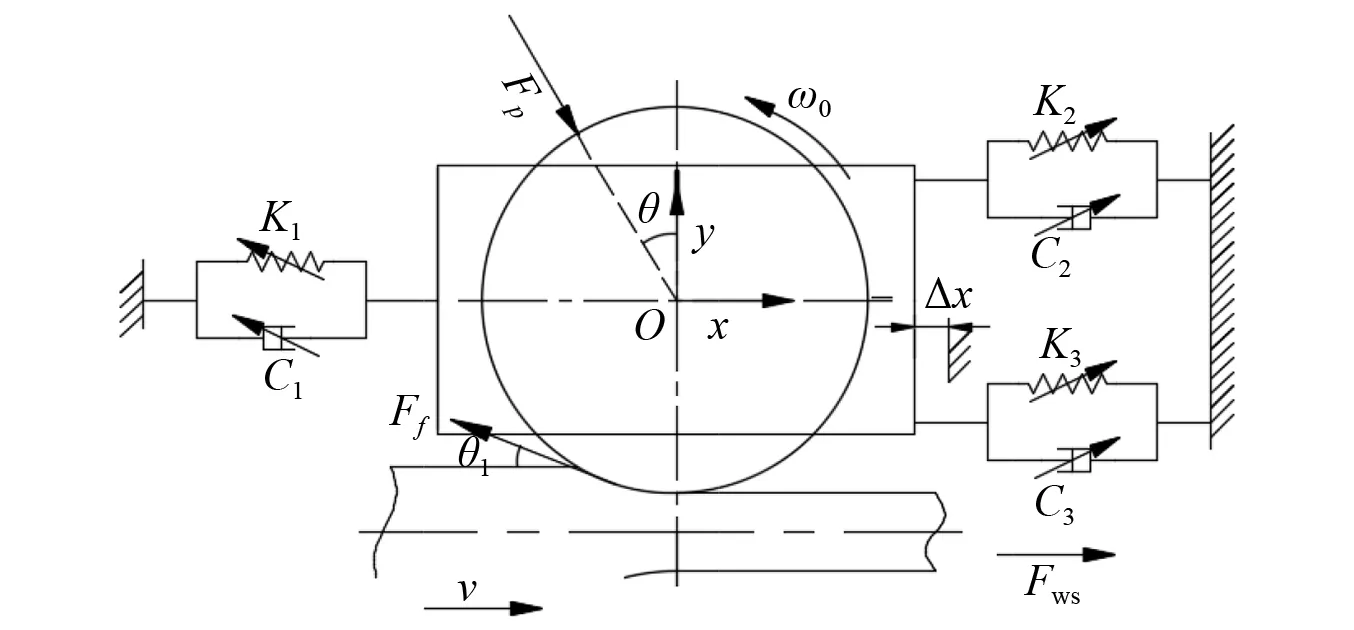
图1 工作辊水平振动动力学模型Fig.1 Dynamic model of horizontal vibration of work roll

辊缝摩擦可以用等效摩擦力来表示

Ff=AFa+(1-A)Fb

(1)

式中：A为真实接触面积比；Fa为边界润滑摩擦；Fb流体动力润滑摩擦力；θ1为摩擦力水平方向夹角。等效摩擦力在水平方向的分力为

F1=Ff×cosθ1

(2)

液压缸通过支撑辊传递给工作辊的水平分力[21]可以表示为

F2=Fpsinθ=Ptanθ

(3)

由式(2)可知，液压缸外激励水平分力与系统轧制力P相关，其中θ为轧机工作辊质心与支撑辊质心连线垂直方向的夹角。

附加水平力[22]可表示为

(4)

式中：φ1，φ2分别为万向接轴和工作辊的旋转角；a为接轴和轧辊轴线夹角；M1为作用在万向接轴的扭矩。

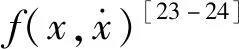
(5)

由于系统激振力由频率不等的三部分组成，基于牛顿定律建立轧机工作辊水平方向运动微分方程

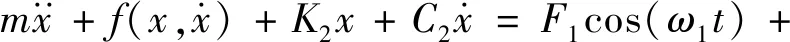
(6)

式中：K1，K2，K3和C1，C2，C3分别为板带、支承辊、牌坊立柱与工作辊之间的刚度和阻尼；ΔX为轴承座与牌坊立柱之间的间隙；ω1，ω2，ω3为系统三项激励不等激振频率。

基于Duffing振子和Rayleigh振子的非线性特性建立轧机系统的动力学模型[25]。

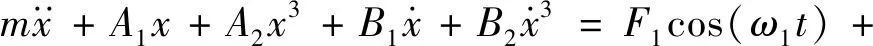
(7)

2 轧机水平振动响应求解

对式(7)进行无量纲处理

(8)

并考虑到弱非线性情况引入小参数ε，得到微分方程为

(9)

根据多尺度法[26]的基本思想，引进自变量

Tn=εnt,n=0,1

(10)

因此关于t的导数变成了关于Tn的偏导数的展开式，即

(11)

将式(11)代入式(7)中，整理方程为

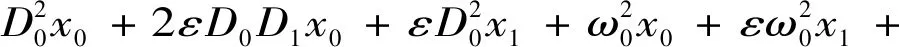
(12)

系统激振力由频率不等的三部分组成

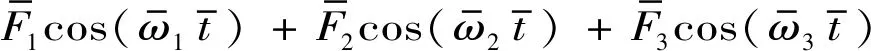
(13)

假定方程的解为

(14)

将式(14)代入式(12)中，令方程两端的ε0和ε的系数相等，就得到

(15)

式(13)第一个方程的通解为

(16)

其中，

(17)

将式(16)代入式(15)第二个方程，结果会得到单频激励项、多个频率激励项，包括两个激励项以及三个激励项。

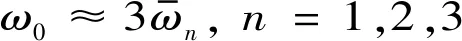
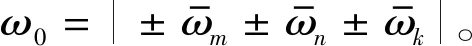
(18)

当满足式(19)条件时，可以消除永年项。

(19)

(20)

经过计算可以得到系统永年项为

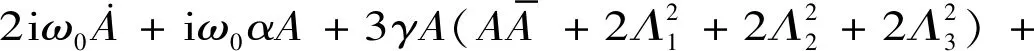
(21)

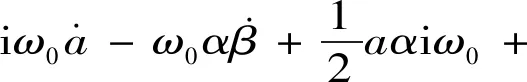
(22)

对式(22)中实虚部分离，令

得到

(23)

得到组合共振的幅频响应方程为

(24)

3 工作辊组合共振仿真分析

为研究冷轧机在多种激励下的组合共振现象，以某冷轧机为例，根据工艺参数及结构尺寸取以下参数：

m=2×104kg、工作辊半径R=0.3 m、压下量ΔH=0.32 mm、A1=2.533×109N·m-1、A2=2.952×1019N·m-1、B1=1.087×106N·s·m-3、B2=1×1010N·s3·m-3、τb=15 MPa、M1=9.98×106N·m、a=7.6° 计算值为：

ω0=1、γ=1.165、η=0.017 8、α=0.153、f1=6、f2=1.25、f3=3.25。

3.1 组合激励下系统幅频响应仿真研究

在存在三项不同频率的组合共振中，刚度系数的变化对轧机振动状态存在一定的影响。

如图2和图3所示，随着刚度项系数的变化，脊骨线位置也会发生偏移，会影响到轧机的固有频率，尤其在图2中，线性刚度系数的微小变化，直接影响到轧机固有频率，并且随着线性刚度系数的增加，组合共振位移响应减小，振动峰值降低，说明选取适当线性刚度系数，能有效避开共振区域。

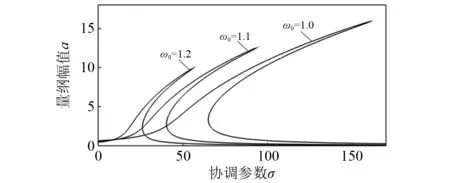
图2 线性刚度变化组合共振幅频曲线Fig.2 Common amplitude-frequency curve of linear stiffness change combination

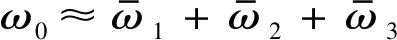
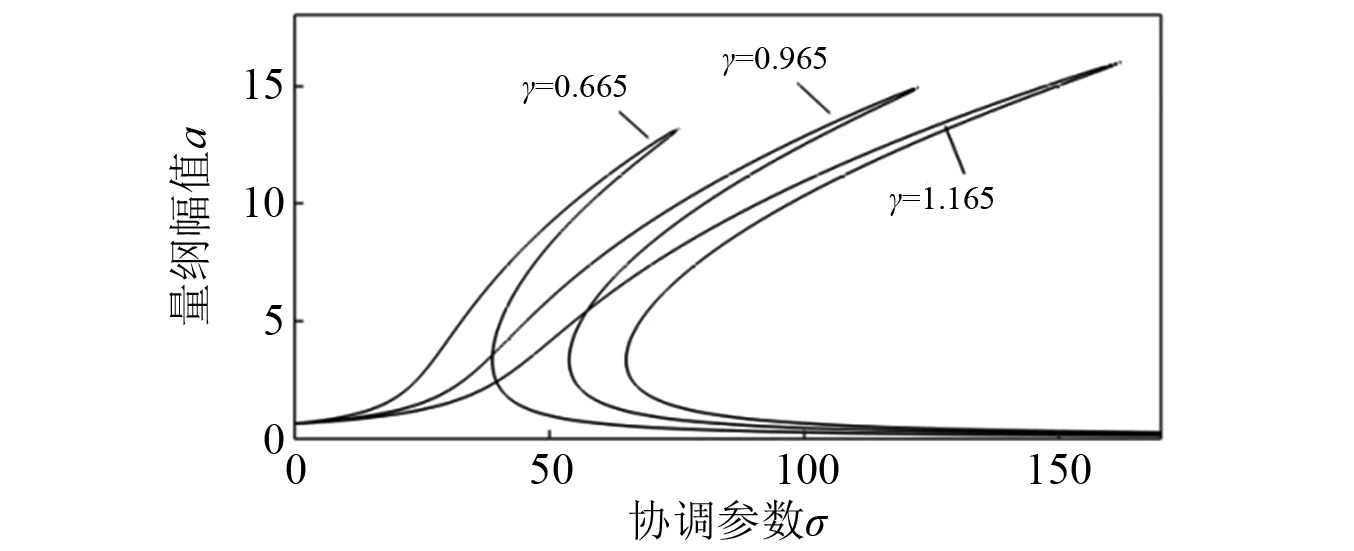
图3 非线性刚度变化组合共振幅频曲线Fig.3 Common amplitude-frequency curve of nonlinear stiffness change combination

图4所示为轧机线性阻尼系数变化对系统幅频特性的影响，图4(a)所示，随之线性阻尼系数的变化，系统脊骨线位置及弯曲度不会发生改变。图4(b)所示随这系统线性阻尼的增大，系统振动幅值降低。但线性阻尼系数的微小变化，并不会使系统振动有明显变化。

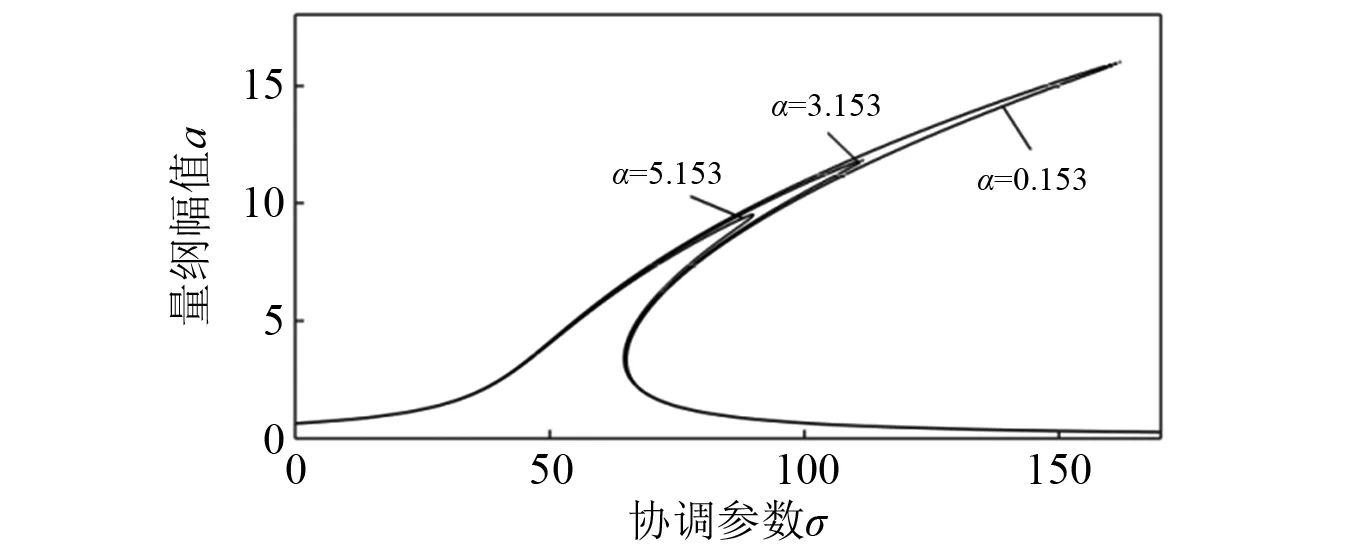
图4 线性阻尼变化组合共振幅频曲线Fig.4 Common amplitude frequency curve of linear damping change combination

图5所示，类似与线性阻尼系数，随之二次项阻尼系数增加系统振动幅值逐渐减小，相比与图4非线性阻尼系数的微小变化对轧机振动影响明显。

图5 非线性阻尼变化组合共振幅频曲线Fig.5 Common amplitude-frequency curve of nonlinear damping change combination

3.2 组合激励下系统响应仿真研究

据式(6)，由轧机结构计算的到的参数进行数值仿真求解，得到系统固有频率为18 Hz,对轧机在组合激励情况下系统水平振动仿真响应如图6所示。图6(a)为轧机水平振动位移，图6中可以看出，系统振动存在明显的非对称现象，即轧机水平振动方向存在着非对称结构，由于工作辊轴承与牌坊立柱之间存在着间隙，轧机工作时会产生撞击现象，对生产设备产生影响。

图6(b)为系统在组合激励下的水平位移响应对应频谱，图中明显表示振动系统的水平位移呈周期、倍周期运动。图6(c)为水平系统响应相图，图6(d)是其庞加莱截面图，图中存在有限个数的点，进一步证明系统处于稳定周期运动，此时系统稳定。

图6 组合振动仿真响应Fig.6 Combined vibration simulation response

3.3 外扰激励幅值对系统分岔行为的影响

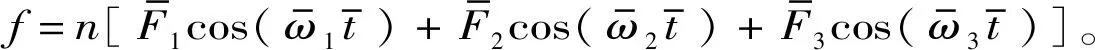
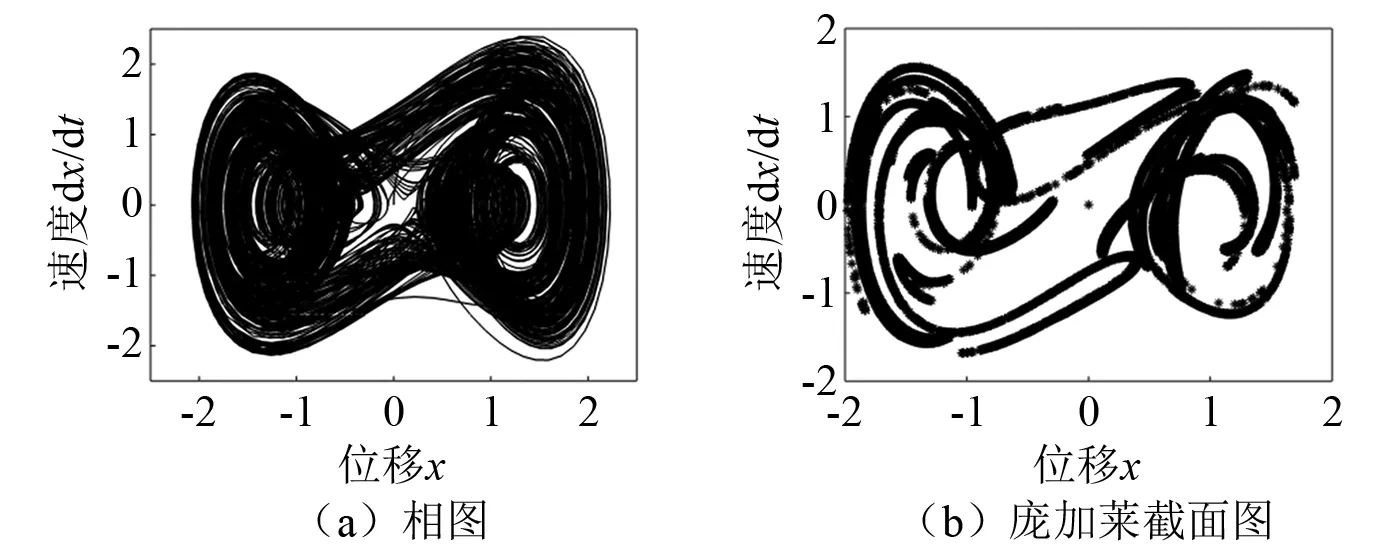
图7 当n=0.25时系统振动特征Fig.7 n=0.25 system vibration characteristics

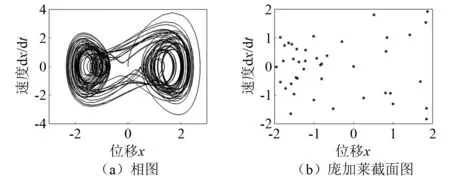
图8 当n=0.55时系统振动特征Fig.8 n=0.55 system vibration characteristics

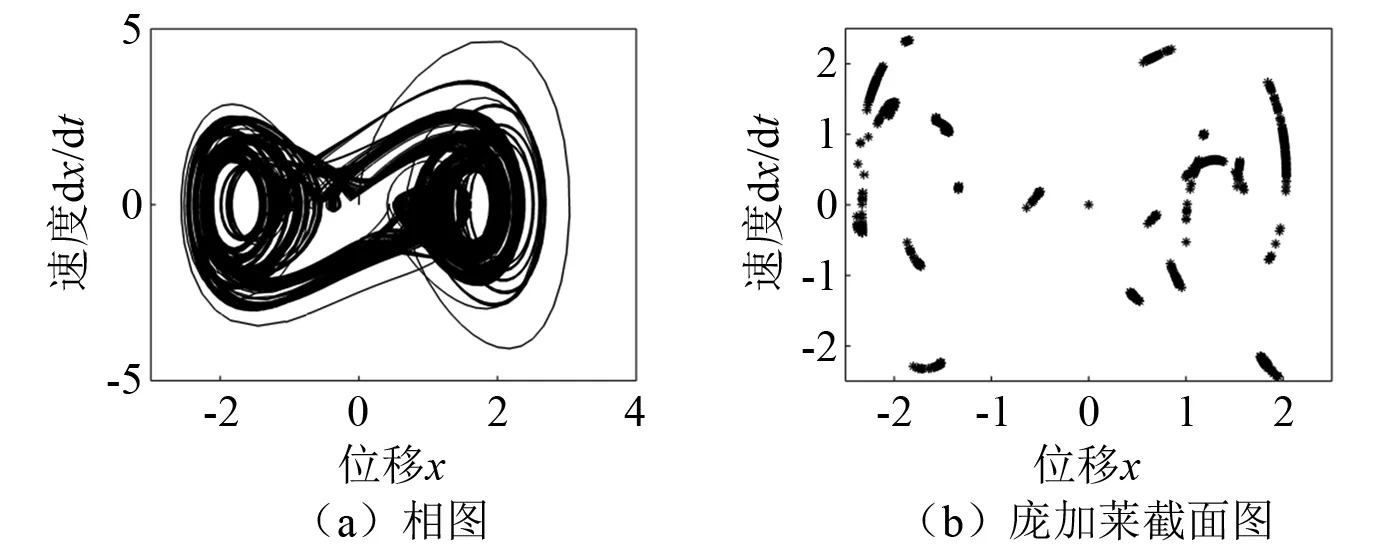
图9 当n=0.8时系统振动特征Fig.9 n=0.8 system vibration characteristics

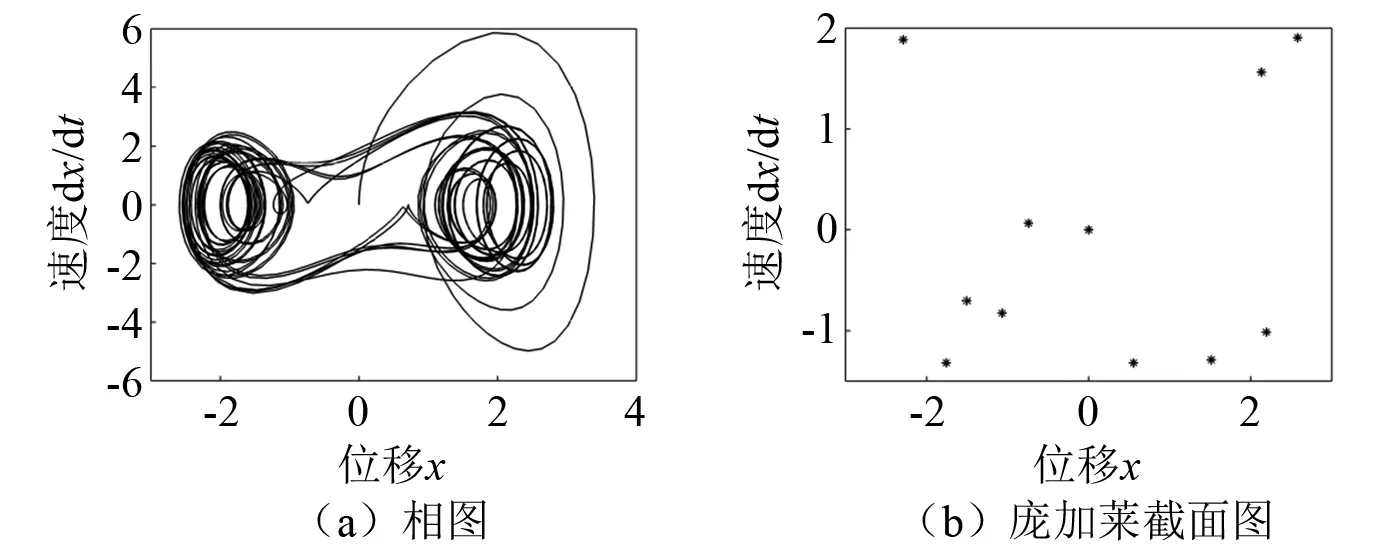
图10 当n=1.1时系统振动特征Fig.10 n=1.1 system vibration characteristics

由图6(c)和图6(d)所示，此时幅值参数为1，得到的庞加莱界面为多个不动的点，此时系统处于倍周期，同样当n=0.55和n=1.10时，系统在截面上留下有限个离散的点，也是属于倍周期运动，此时系统是稳定的。但在n=0.25和n=0.80时系统在界面上留下成片的点集且具有相似性，故此种状态下水平振动系统处于混沌周期，此时系统不稳定。

为研究组合振动中外扰力幅值对轧机水平振动周期特征的影响分布，对非线性系统进行更深入的数值仿真的到对应的分叉图。如图11当n在0.01～0.30时处于混沌周期随后过度进入一段范围的倍周期状态(0.30～0.62)，再过度到混沌周期状态，当n值快接近1及往后系统一直处于稳定的倍周期运动状态，与图7～图10仿真结论吻合。

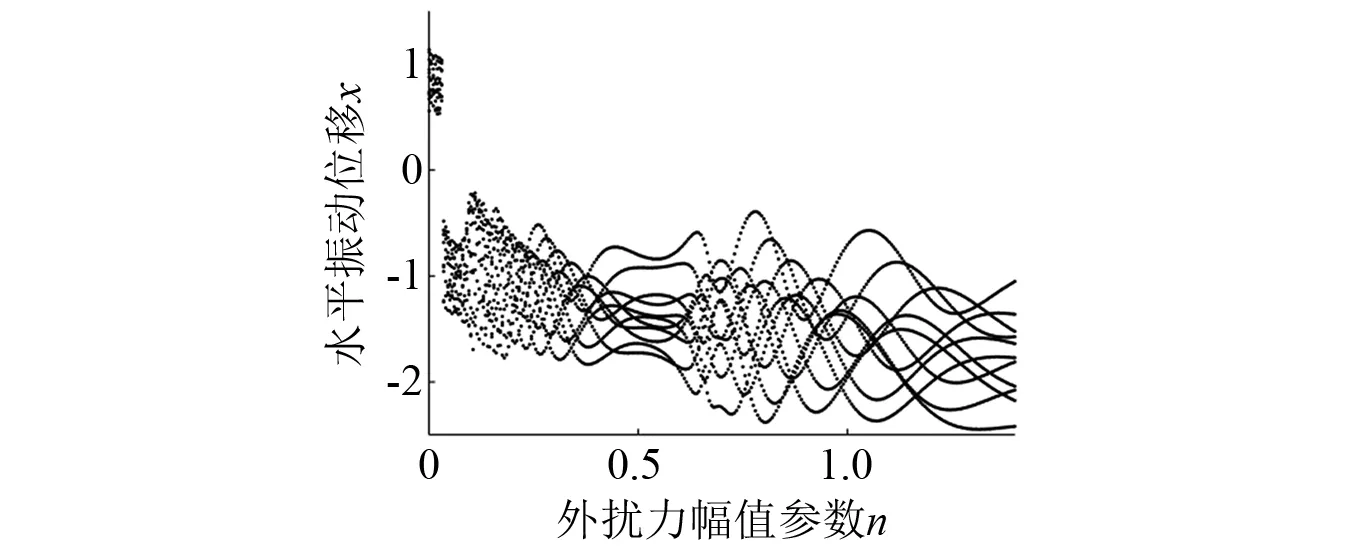
图11 幅值变化的系统分叉图Fig.11 Bifurcation diagram of the system with amplitude changes

3.4 系统水平结构间隙对振动位移的影响

在图6(a)中得出，在轧机水平系统中由于轴承座与牌坊立柱存在间隙，造成系统的碰撞。图12(a)为21组系统响应时间在0.5～2.5 s时的位移响应图，在图12(b)中可知，系统存在间隙时，水平振动位移为非对称的，但是随着间隙的减小，系统振动正负位移差会逐渐减小，同时系统正负位移趋于对称，在间隙为0时，系统最为稳定。证明减小轴承座与牌坊立柱之间的间隙，能极大减小系统振动位移，降低设备碰撞损害。

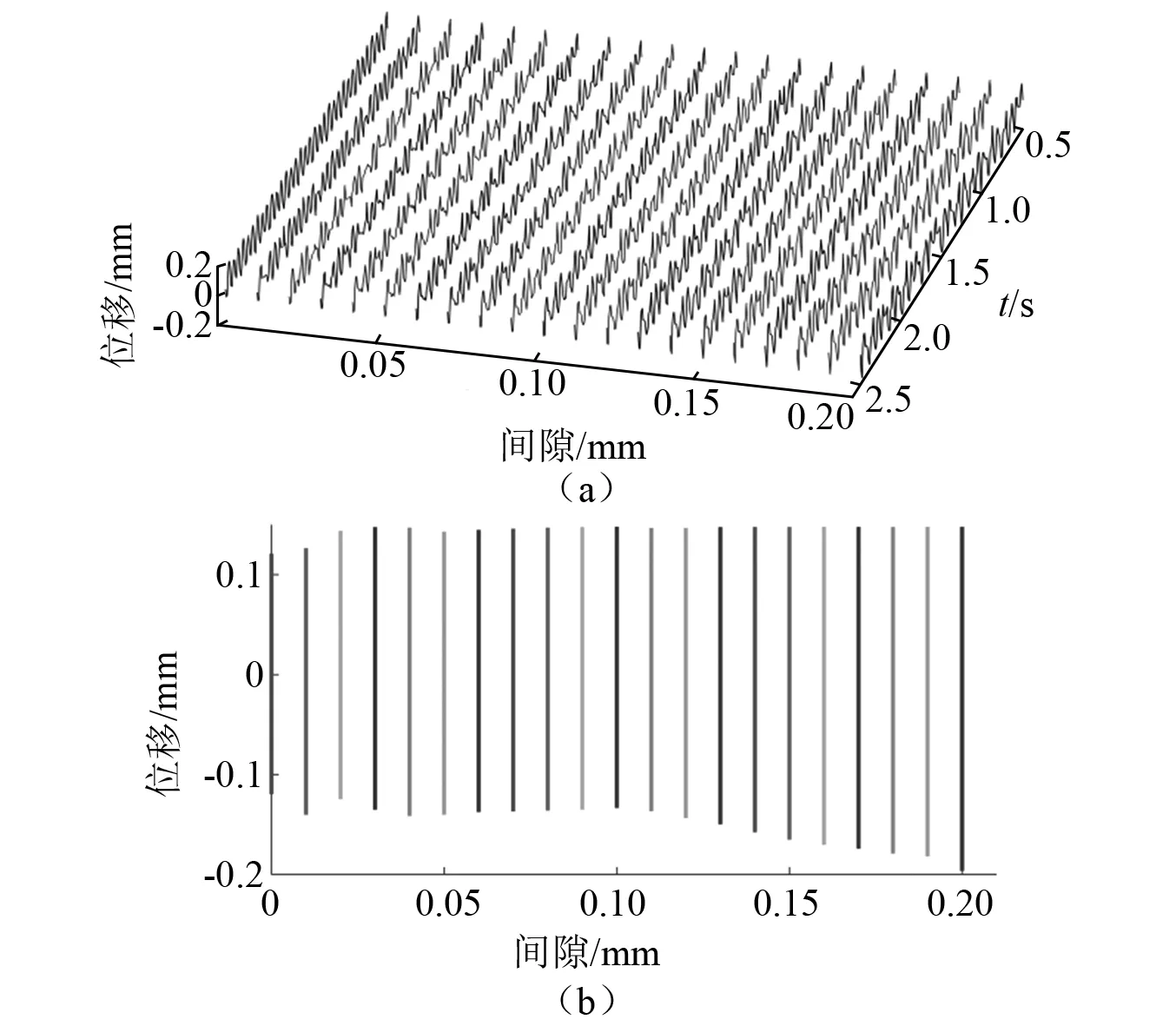
图12 轧机间隙变化水平振动响应图Fig.12 Horizontal vibration response diagram of rolling mill gap change

4 结 论

本文建立冷轧机在组合激励下，上工作辊水平振动动力学模型，经过计算仿真得到如下结论：

(1) 当三种激励频率之和接近固有频率时，计算得到系统的幅频特性响应方程，通过仿真发现，由于二次项刚度系数的存在，系统的幅频特征曲线会出现脊骨线弯曲，出现明显的跳跃和滞后现象，使在两次跳跃之间出现不稳定区域。通过对系统刚度系数和阻尼系数的调整，有效避开系统振动区域减小振动幅值。

(2) 通过系统响应仿真发现，由于轧机轴承座与牌坊立柱存在间隙，致使在组合激励下系统水平振动非对称位移，又通过对系统频谱图、相图及庞加莱截面图的分析发现此时在组合激励下，系统属于周期、倍周期运动。通过改变系统组合激振力的幅值发现系统随系统激励幅值的变化，系统振动周期倍周期与混沌周期特征会交替出现，仿真发现外激励幅值取一定范围时有利于抑制轧机水平系统混沌运动的产生。改变系统水平方向的结构间隙，发现随着间隙的减小不仅会降低系统的撞击现象还会降低水平振动幅值，有利于抑制轧机的水平振动。