三浦折纸超材料结构数字化设计与模型验证1)
陈 耀 叶王杰 史佳遥 冯 健
(东南大学混凝土及预应力混凝土结构教育部重点实验室,国家预应力工程技术研究中心,南京 211189)
引言
近年来,随着计算机科学、计算几何学和数论等领域的发展[1],折纸折痕分析及设计技术快速发展[2-5],以折痕设计为核心研究内容的折纸结构受到各领域研究人员的青睐.折纸结构已应用于土木建筑[2]、航空航天[6-7]、柔性电子[8]、生物医学[9-11]、超材料[12-15]、机器人[16-18]、光学[19]等领域.
早期,折纸仅作为一项满足人们审美需求的艺术形式,Yoshizawa 等创造了可供人们交流的折纸语言,并通过平面几何、立体几何、微分几何、球面三角学理论等数学原理建立了折纸艺术与折纸科学之间的联系[20].此后,折纸艺术不断发展成为现代折纸科学.Miura(三浦)[21]率先发明了三浦折纸构型(又称三浦折叠),并将其应用于可折展的太阳能帆板.另一方面,超材料由于具有可调节的材料特性,近年来发展迅猛,Yu 等[22]综述了各种力学超材料胞元结构拓扑优化的重要进展,其中包括蜂窝结构、晶格结构和折纸超材料结构,分析了其弹性模量、泊松比、体积模量等与常规结构不同的材料特性.Fang 等[23]深入研究了四折痕折纸基本单元组合的自锁特性,为开发拥有可编程性能的折纸超材料提供了有效途径.Wang 等[24]研究了一种基于三浦折叠的折纸超材料,可通过几何重构和形态变化主动调整材料的电磁和力学性能.
为了便于生成折纸结构的复杂三维模型、推广应用于缓冲吸能结构及可展结构,诸多学者对三浦折纸构型开展了深入研究与衍生拓展.Gattas 等[25]考虑了折痕方向、折痕形式、结构的可展性与平面折叠性等因素,提出了广义三浦折纸构型的设计方法.文献[26-28]建立了折纸折痕构型的图论表达方法,并结合优化算法研发了多种新型折纸构型.基于经典三浦折纸模式,Gattas 和You[29]提出了一种曲线折痕折纸构型的参数化设计方法.此外,为了将折纸构型应用于非零厚度的三维结构,Chen 等[30]引入三浦折纸的机构运动学模型,并推广至厚板折纸结构.文献[31-33]基于图论方法,提出了一种利用无向和有向子图生成二维折痕图案的方法,为折纸结构开展几何、力学性能分析等提供了便利.Li 等[34]综述了近年来折纸超材料的几何设计、力学分析、性能实现和制造技术之间协同等.Tachi[35]指出,将折纸应用于现实生活时,控制其三维构型极为重要,以便产生的折叠状态与所需的功能、结构和环境等协调统一.Mattoccia 等[36]利用Grasshopper/Rhino 软件,对单层零厚度的三浦折叠结构进行了参数化建模,以便利用几何参数控制最终的折纸构型.Curlettod 和Gambarotta[37]考虑了相邻模块运动兼容性条件,建立了基于Waterbomb折痕图案的参数化模型,通过给定角度来获得不同折展状态下的折纸模型.Wonoto 等[38]综合采用数字化设计和有限元分析工具,分析了可展开折纸的几何特性,探讨了将微观结构的几何和机械原理用于建筑元素的可能性.此外,部分学者提出了可用于折纸构型初步设计的计算程序或插件[25-26,35,39].
然而,已有方法往往更侧重如何将二维纸张按特定折痕转化为三维构型,且已有的参数化模型大多为单层、零厚度折纸模型.如何依据特征几何参数快速、准确生成多层堆叠的复杂三维模型、尤其是非零厚度实体模型,如何根据结构实际需求实现科学合理的结构逆向设计,仍是折纸结构数字化设计亟待解决的难题.为此,本文拟基于三浦折纸胞元以及超材料的构成规律,综合利用Matlab 和Grasshopper 软件,搭建折纸超材料结构数字化设计平台,深入探索折痕总长、相对密度、折叠率等指标的演变规律,并辅以部分3D 打印物理模型及有限元分析模型进行验证分析,以实现零厚度及非零厚度复杂折纸结构模型的高效、一体化建模,同时可为该类折纸结构的力学性能模拟、试验研究及工程应用等奠定较好的基础.
1 几何构型
图1(a)所示为三浦折纸基本胞元的半折叠构型,单个胞元由四个平行四边形组成.其实,胞元的几何构型可通过多种方式参数化,这里采用的是两个静态折痕长度a,b以及一个静态内角 γ 定义折叠模式,同时用四边形平面与XY平面的二面角 θ 来量化折叠程度[30].令X和Y为结构平面内坐标,Z为面外坐标,则结构几何构型可由以下尺寸参数确定


图1 折纸超材料结构模型Fig.1 An origami metamaterial structural model
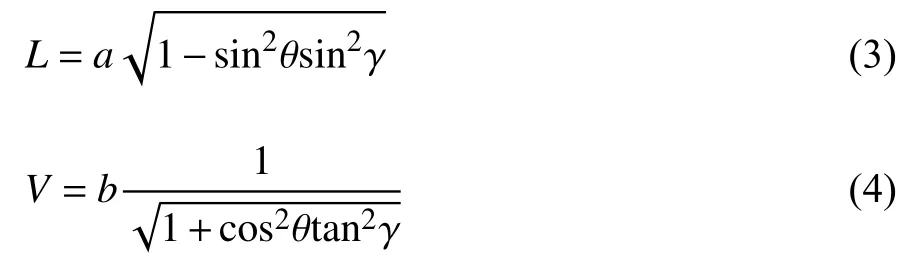
式中,H为结构沿Z向高度,2S为结构沿X向的长度,2L+V为结构沿Y向长度.将上述胞元按照M×N(图1(b)中M=N=5)的排列模式拼接成三浦折叠薄壳结构,其中M和N分别为X向和Y向胞元个数.部分折叠的三浦折叠薄板可视为薄壳结构,值得指出的是,折叠模式可有效改变薄壳结构的整体力学性质(例如负泊松比).
根据三浦折纸基本单元的几何构型,可发现胞元在X和Y两个方向膨胀的耦合仅取决于边长b与Y轴的夹角.因此,具有不同高度H的三浦折叠薄壳可以堆叠在一起,并沿着折叠线粘合起来,同时保持自由折叠的特性,其结果即图1(c)所示的三浦折叠超材料.假设三浦折叠壳在堆叠时按照ABABAB的模式,在Z向重复堆叠O组,为了确保A和B层薄壳在折展过程中的几何协调性,两层薄壳的几何构型需满足:SA=SB,VA=VB,LA=LB,且HB≥HA(即γB≥γA).因此,B层薄壳相对应的几何参数需满足
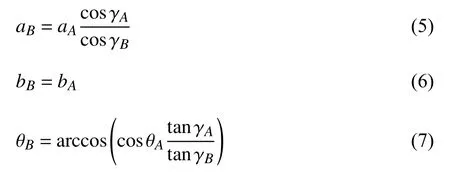
由上可知,三浦折叠超材料的主要几何参数为面板厚度h,A层薄壳面板面内角γA,B层薄壳面板面内角γB,A层薄壳面板倾角θB∈[0,π/2],A层薄壳面板边长aA和A层薄壳面板边长bA.图1(c)所示M×N×O=5×5×6 的超材料模型作为结构标准模型.
2 结构构型的数字化设计
2.1 Rhinoceros 几何参数建模
传统建模或找形方法难以生成复杂的三维折纸结构模型,且参数分析时往往需要大量、重复性的建模与调整,工作量巨大.另一方面,如何根据折纸结构的实际需求合理完成结构的逆向设计,亟待解决.为此,本文利用犀牛及其可视化编程插件Grasshopper,实现了三浦折纸超材料结构数字化快速建模,为复杂折纸结构的正向与逆向设计搭建桥梁.结合软件内置电池实现特定的几何建模,将建模过程转化为有逻辑性的模块连接,参数化面板的部分树形结构如图2 所示.
图2 Grasshopper 参数化面板Fig.2 Grasshopper parametric panel
需指出,三维实体模型便于结构的3D 打印及精细化有限元分析等,往往可通过中间层的面偏移方式构建.然而,三浦折纸超材料模型每个基本单元均是由不同角度的空间面板组成,面偏移的方式会使得不同角度的面板与相邻面板发生交融或空缺,需进行大量的修剪和填补工作.为避免该问题,选用结构侧截面沿指定路径挤出的方式建立三维实体.
尽管上文几何构型分析确定了结构的五个主要参数,但并不便于直接建模.如图3 所示,结构数字化建模需通过几何推导,求得XZ平面上基本单元的参数和XY平面上挤出路径的参数.随后,通过已确定的M,N,O数值与实体模型厚度参数h生成XZ平面上的基准面与XY平面上的路径.最后,将基准面沿着路径挤出得到实体模型.几何关系如下
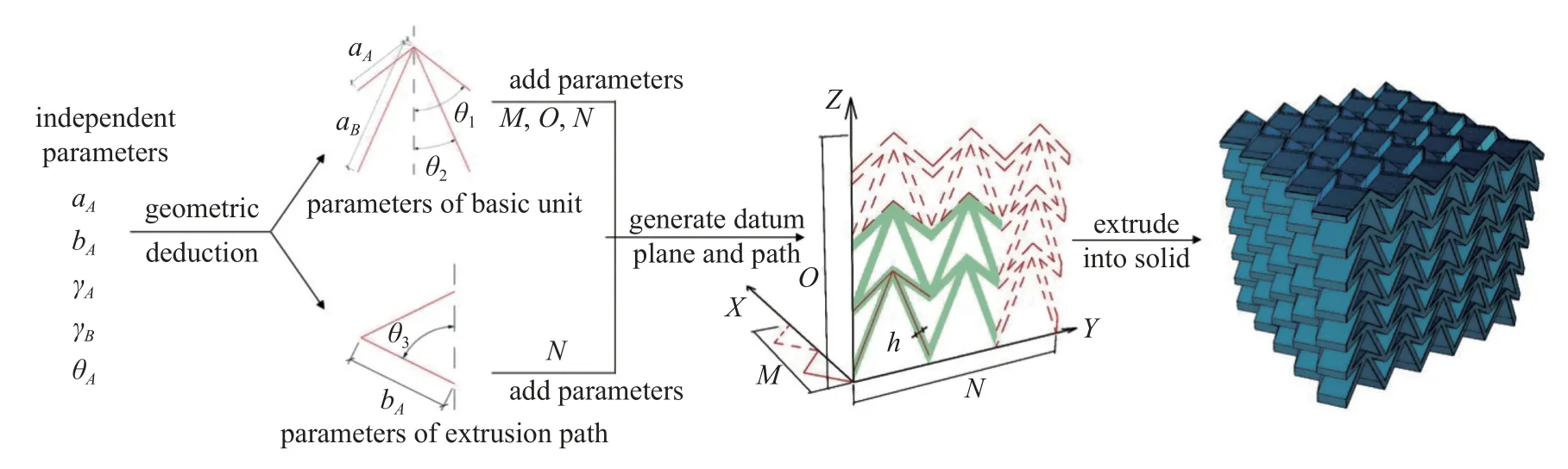
图3 数字化建模流程Fig.3 Digital modeling process

其中fA和fB分别为aA和aB的单侧偏移长度.
该过程实现了仅需输入5 个独立参数、3 个方向的堆叠个数和模型厚度共9 个参数,便能便捷地实现折纸超材料结构的数字化建模.值得注意的是,该方法实现了零厚度折纸超材料模型与非零厚度三维实体模型的统一建模,当各层折纸面板厚度参数取为零值时,实体结构即降阶为等效的三维薄壳模型.
2.2 物理模型验证
为验证参数化建模的可行性及精确性,对三浦折纸超材料结构进行了物理模型验证.3D 打印技术是一种以数字模型文件为基础,通过材料的空间堆叠而快速实现实体化的技术,现广泛应用于汽车、航空航天、微机电系统、生物医疗等领域.熔融沉积法(FDM)是众多3D 打印方法中使用最广泛的,通过加热喷嘴融化线材,沉积于工作区域并固化成型,由数字模型文件控制分层工作区域.FDM 型3D 打印机可打印热塑型聚氨酯(TPU)、聚乳酸(PLA)、聚苯乙烯等材料.
本文采用熔融沉积法,选用PLA,Agilus30 树脂以及TPU 材料,打印制作了6 个实物模型(图4),对上述三浦折纸超材料结构进行物理模型验证(模型参数见表1),其中γA=60°,γB=75°.
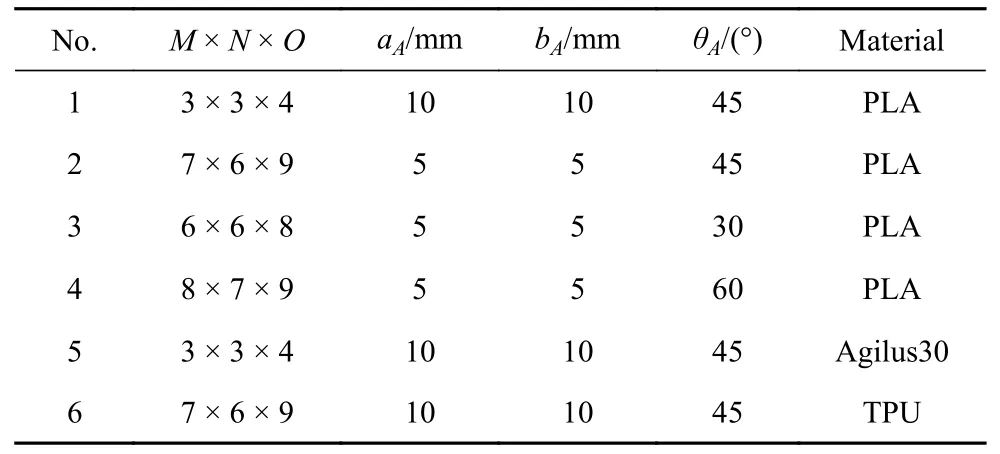
表1 3D 打印实物模型参数Table 1 Parameters for physical models by 3D printing
由图4 可知,尽管构型复杂、单元厚度极薄,3D 实物模型可精确打印,结构壁厚均匀、表面光滑,完成度极高.模型用料量、面板尺寸及壁厚均与数字化模型高度吻合(相对误差小于0.5%),因此验证了折纸结构数字化、参数化建模的准确性.值得一提的是,与图4(a)结构相比,图4(e)模型选用更柔的Agilus30 树脂材料3D 打印而成、其他参数不变,由于Agilus30 树脂具备较理想的变形能力,该结构可反复、平顺地从展开状态压缩至紧凑的折叠状态,反之亦然.

图4 三浦折叠超材料结构模型验证Fig.4 3D printing and digital Miura-ori metamaterial structural models
3D 打印技术和FDM 操作方便,设备成熟度高,可选用的材料较为丰富,折纸超材料构型复杂,相比传统结构加工方法成本高且耗时长,更适合采用3D 打印技术.此外,使用的多为塑料质材料,模型的表面光滑,不需要后续处理,有利于折纸超材料结构的后续研究.诚然,3D 打印制作折纸超材料结构仍存在一定的局限性,例如结构力学性能有待进一步研究、加工时长及成本较高、材料选型有限等.
3 几何特性与结构选型
3.1 几何特性
3.1.1 折痕长度
不失一般性,令三浦折纸超材料结构的三向胞元个数为M×N×O,共包含有4M×N×O个平行四边形面板,面板之间通过公共边(折痕)相连.近期研究已表明[5,40-41],多折痕折纸管在折展变形时,折痕处应变明显高于面板且吸收了大部分能量.可知,折痕总长度不仅影响结构的吸能性能,而且影响实际构件的制作难度与成本.因此,需对不同几何参数下结构折痕总长进行对比分析.
折痕总长度由以下两部分组成:两个平行四边形面板之间的连接处折痕长度L1和四个平行四边形面板之间的连接折痕长度L2,其中L2存在于AB两个单层薄壳的连接处.推导了折痕长度的解析表达
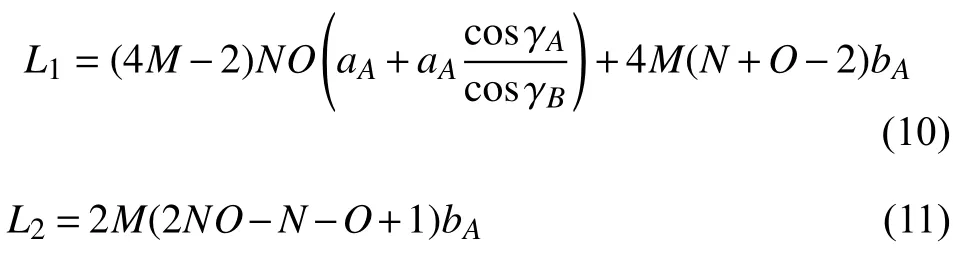
由式(10)可见,L1随着平行四边形面板边长aA和bA的增大而增大;由式(11)可见,L1与bA线性相关.针对标准模型,取aA=10 mm,bA=10 mm代入式(10)和式(11)得
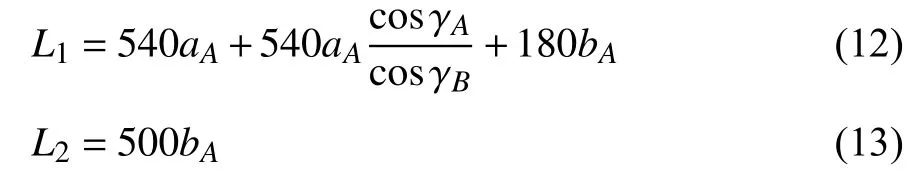
折痕长度L1与γA及γB的关系如图5 所示,可以发现,在其他条件相同的情况下,L1随着γA的增大而减小.对于不同的γB,L1的最小值均相等,数值为12.6 m,且只有在γA=γB时L1达到最小值,这一点在L1的表达式(10)中可得到验证.

图5 不同γB 情况下L1 与γA 的关系曲线 (M=N=5)Fig.5 Change curve of L1 with γA under different γB conditions(M=N=5)
3.1.2 相对密度
三浦折纸超材料结构应用于缓冲吸能时,不仅需要评估结构吸能的能力,同时要考虑结构的相对密度大小,相对密度较小却拥有较好的吸能能力是性能优异吸能材料的优势,同时可以降低材料的制作成本[5,27].推导了X,Y,Z向堆叠数量为M,N,O的一般模型的相对密度,解析表达如下
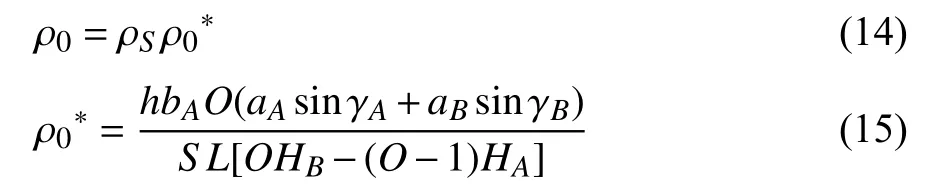
式中,ρ0为材料密度,ρS和ρ0*分别是基材的密度和超材料的相对密度.
将式(1)~式(4)代入式(15)可得
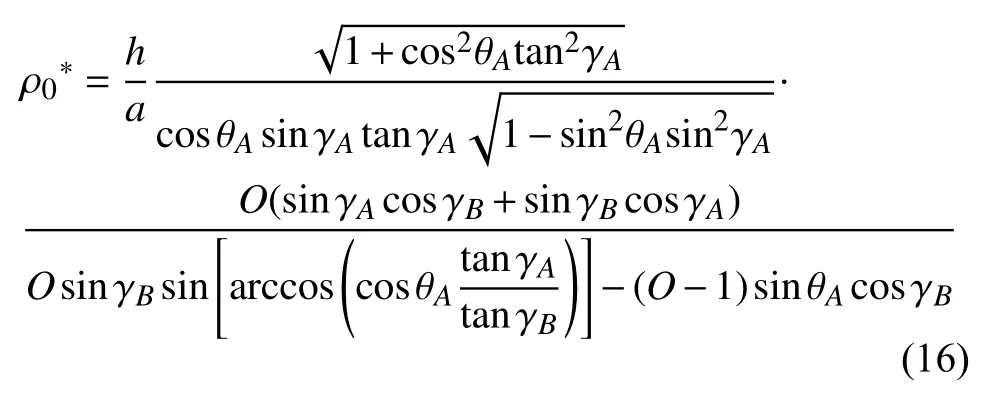
当O值较大时,该式可简化为
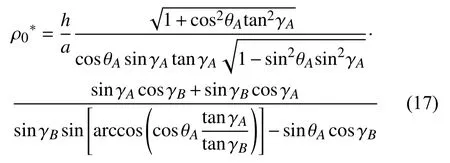
根据式(14)可知,对于给定的锐角γA和γB、边长bA和四边形平面与XY平面之间的二面角θA,相对密度h/a成正比,且不受边长bA的影响.针对γA,γB和θA对模型相对密度的影响,选取标准模型具体分析,其中aA=10 mm,bA=10 mm,θA=45°,h=0.3 mm.根据式(16)求得标准模型的相对密度
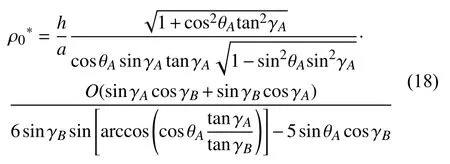
图6(a)描绘了标准模型的相对密度在不同γA和γB组合下的变化情况,可以发现γB保持不变时,相对密度随着γA的增大先减小后增大.每条密度曲线均存在有一个最小值,且随着γB的减小,最小密度所对应的γA相应地减小.θA同样会影响超材料的相对密度,由图6(b)可知,ρ0*随着θA的增大而增大,且增速逐渐变大.

图6 相对密度理论曲线Fig.6 Theoretical curve for relative density
3.1.3 折叠率
折叠率是可展结构、折纸结构的重要指标之一,可体现结构的折展效率,一般采用结构折叠前所占面积、体积与折叠后所占面积、体积的比例来具体描述.对于可展结构,折叠率越高则结构的折展效果越好[2,27],便于存储、运输;对于吸能耗能结构,高折叠率的结构往往具有更优异、充分的形变空间和塑性变形,因此往往能耗散更多的塑性应变能[40,42-44].
令模型的折叠率ζV为结构完全展开至图7(自锁)时的体积与完全压缩态下的体积比,三向堆叠数M×N×O的一般模型的折叠率计算如下

图7 标准模型沿X 方向完全展开构型Fig.7 Fully deployed configuration of reference model along direction X
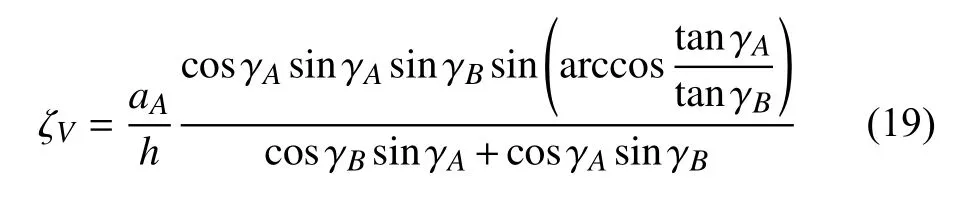
由式(19)可知,折叠率仅与aA,h,γA,γB相关,与aA/h成正比例.例如,取aA=10 mm,h=0.3 mm,可获得折叠率随角度γA和γB的演变规律,如图8所示.
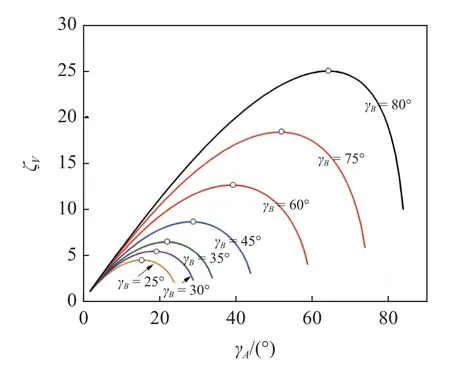
图8 折叠率ζV 与γA 及γB 的关系曲线Fig.8 Relation curve of maximum folding ratio ζV with γA and γB
可以发现,γB保持不变时,ζV随着γA的增大先增大后减小.每条折叠率曲线存在一个最大值,γB越大的曲线对应的折叠率最大值越大,且随着γB的增大,最大值所对应的γA相应地增大.
3.2 数字化设计误差分析
为进一步验证本文数字化设计方案的正确性,将其更准确地应用于三浦折纸超材料结构的选型优化,本节结合几何特性的理论推导进行验证.
为验证所推导折痕长度的准确性,分别选取图5 中γA=30°,γB=50°;γA=40°,γB=60°;γA=45°,γB=65°;γA=55°,γB=70°;γA=60°,γB=75°五组模型数据,利用数字化建模技术建立三维模型,并求得对应实体模型的折痕长度L1,如图5 中的散点数据所示.对比可发现,L1理论值与实体模型中的长度吻合较好,相对误差分别为1.64%,1.00%,0.82%,0.79%,0.64%.
为了验证所推导相对密度的准确性,分别选取γB=35°,γB=45°,γB=60°,γB=75°,γB=85°五组相对密度曲线上的理论最低值点,利用数字化建模技术建立一系列三维模型,并求取对应实物模型的相对密度,即图6(a)中的散点.求得相对误差分别为23.9%,16.01%,5.05%,-8.29%,2.76%,图9 为其中部分三维数字化模型示意.由于γA,γB较小时相邻面板间夹角较小,实体模型需要填补的空缺体积较大,因而相对误差较大,其余几组与理论值吻合较好.
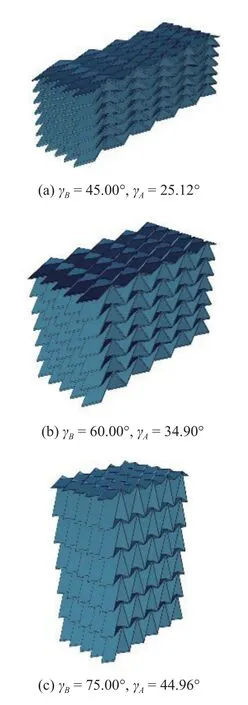
图9 不同γA 的部分三维模型示意Fig.9 3D models with different γA
此外,为进一步验证推导所得相对密度与θA的变化关系,选取图6(b)中θA=20°,θA=30°,θA=50°,θA=70°,θA=80°五组参数建立实体模型,见图10,求得对应的相对密度值,即图6(b)中散点.求得的相对误差分别为3.15%,1.67%,-2.55%,-9.39%,-20.00%.
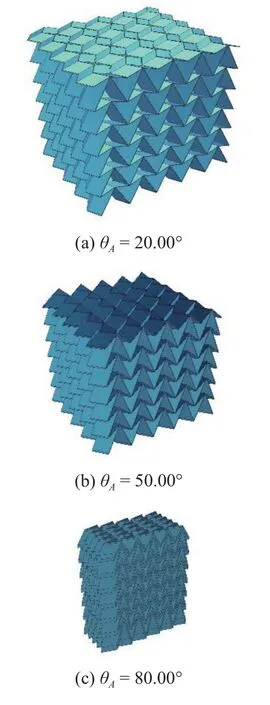
图10 不同θA 的部分三维模型示意Fig.10 3D models with different θA
3.3 准静态压缩过程分析
由于折纸结构轻质节材、耗能优异等特点,常作为薄壁吸能耗能结构应用于诸多领域[42-44].为揭示相对密度对三浦折纸超材料结构吸能效率的影响规律,利用Abaqus/Explicit 对其进行准静态压缩过程分析与验证.将超材料结构放置在一个固定的刚性平面和一个可在压缩方向移动的刚性平面之间.结构自身选通用接触,摩擦系数为0.3,与刚性面板之间设置点面耦合.设置位移荷载,其值为结构压缩方向长度的70%,并设置平滑分析步以保证收敛性.超材料结构网格类型选用S4 R 积分四边形单元,尺寸选为3,刚性面板选用R3D4 单元.令计算结果中动能与内能之比小于5%,以保证动力效应可忽略不计;伪应变能与内能之比小于10%,以避免沙漏效应对结果带来的影响.
由式(12)、式(13)和式(17)可知,自变量θA的变化不引起折痕长度的变化,但会使相对密度发生改变.选用标准模型,取γA=60°,γB=75°,aA=aB=10 mm,h=0.3 mm,模型参数如表2 所示.材料均选用6061-T6 铝合金,密度2750 kg/m3,弹性模量70 GPa,泊松比0.3,屈服极限300 MPa.
例如,图11(a)描述了其中模型Mi-3 的压缩变形过程,当该结构模型受图1(a)所示X轴方向的轴向压缩作用时,X向产生显著的压缩变形,同时沿Y和Z向收缩,结构呈现出显著的负泊松比效应.
五组模型的力位移曲线如图11(b)所示,这里引进一个能更好体现结构轻量化的指标SEA (specific energy absorption)[40,43-44],即单位质量的吸能能力,其计算方法如下

图11 三浦折纸超材料结构压缩性能分析Fig.11 FEM results for Miura-ori metamaterial structures under quasistatic compressions

其中,E为压缩过程中吸收的总能量,m为模型质量.计算结果见表2.
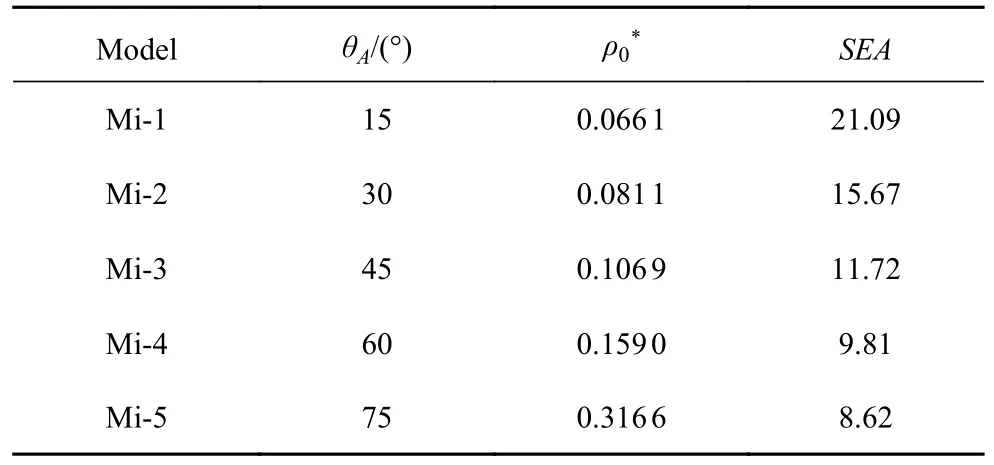
表2 模型参数与模拟结果Table 2 Parameters and FEM results for different models
由表中数据可知,A 层面板倾角θA的增大不改变模型的质量,相对密度增大,SEA反而减小,即模型的吸能效率降低,同时由式(11)和式(12)可知此时模型的折痕长度不发生变化.可知在A 和B 层胞元面板构型、折痕总长度及面板厚度不变的前提下,三浦折纸超材料结构的相对密度与比吸能成反比关系.因此,结构选型时,可根据图6 选取相对密度较小的变量组合.
4 结论
本文基于三浦折叠胞元以及三浦折纸超材料的几何构型,给出了决定构型的几何参数,对工程应用中较为关注的超材料结构折痕总长、相对密度及折叠率等指标,系统推导了一般模型的理论表达式,并揭示了以上特性与三浦折纸超材料结构几何参数的演变规律.选定标准模型,探究得γA=γB时折痕总长L1最短,折痕总长L2的大小仅与B 层胞元边长bA有关,可根据结构需求取折痕长度的参数组合;分析求得使三浦折纸超材料结构折叠率达到峰值的面内角γA和γB组合;由系列模型的准静态压缩分析结果可知,当结构面板构型及折痕总长不变时,较小的结构相对密度可显著提高吸能效率,构型选择时应寻求相对密度较小的参数组合,从而降低质量和成本、提高吸能效率.上述结论对不同性能需求下结构几何参数选取具有指导意义,有利于折纸结构的正向、逆向设计.
利用Matlab 和Grasshopper 实现了零厚度及非零厚度折纸超材料模型的数字化设计.对比折痕长度、相对密度的理论值与实体模型计算值,验证了数字化建模的正确性,为部分超材料结构的参数化建模提供了可行思路,也为三浦折纸超材料结构的后续研究提供了极大便利.
此外,利用3D 打印技术开展了物理模型验证,3D 打印折纸模型可实现模型流程化与标准化建造、降低制作工效与成本,再次验证了数字化建模的正确性,是将3D 打印技术应用于折纸结构智能建造的一项重要实践,对后续折纸研究亦有参考价值.

