基于统一强度理论的非静水压圆形隧道塑性区半径的脆塑性摄动解1)

张常光 李宗辉 关港辉 孙 松

* (长安大学建筑工程学院,西安 710061)

† (地质灾害防治与地质环境保护国家重点实验室,成都 610059)

引言

隧道工程在国家重大基础设施投资中的份额高,针对复杂地质环境的隧道弹塑性分析及支护设计具有重要工程应用价值,其中常用侧压力系数表示水平地应力与竖向地应力存在明显差异的非静水压力为隧道所处真实地应力场的鲜明特征,静水压力下隧道的计算理论不再适用.目前,基于Mohr-Coulomb 强度准则和理想弹塑性模型,众多学者采用Kastner 法[1-7]、复变函数法[8-12]、总荷载不变法[13-15](弹-脆-塑性模型)、数值模拟[16]和摄动法[17-18],探讨了非静水压力下圆形隧道的非圆塑性区边界线.

Kastner[1]将非静水压力下圆形隧道处于纯弹性状态时应力的基尔希公式代入Mohr-Coulomb 强度准则以确定隧道的非圆塑性区边界线.王卫军等[2-3]和郭晓菲等[4]基于Kastner 法提出隧道的蝶形塑性区概念,Yuan 等[5]和Zou 等[6]将基尔希公式代入统一强度理论建立了隧道非圆塑性区的边界线方程,于学馥等[7]考虑塑性应力重分布修正了Kastner法.值得注意的是,Kastner 法忽略了围岩的弹塑性发展过程,近似地将纯弹性状态下基尔希公式直接代入围岩强度准则,但非静水压力下隧道的塑性区边界线不是圆形.

Wang 等[8]、Yan 等[9]和吕爱钟等[10-12]采用复变函数法将非圆形的隧道塑性区边界线保角映射为圆形求解,逻辑上合理但分析过程和公式都较为复杂.严克强[13]、董海龙等[14-15]由总荷载不变法推导了隧道水平或竖向的塑性区半径,而其他方位处的需由相似原理给出.Bagheri 等[16]通过二维弹塑性有限元数值模拟获得了隧道的非圆塑性区,但与模型边界、网格尺寸等密切相关.魏悦广[17]和Tang 等[18]基于摄动法将隧道非圆塑性区边界和弹性区应力求解转化为数学微分方程,计算精度高、误差小.此外,Kabwe 等[19]采用Drucker-Prager 强度准则对非圆形隧道进行了理想弹塑性分析.

岩石真三轴试验表明[20-23]:中间主应力对岩石强度的提高作用明显,Mohr-Coulomb 强度准则未考虑中间主应力而低估了岩石强度,统一强度理论[24]合理考虑了岩土材料强度的中间主应力效应.同时,岩石峰后强度相比峰前常有较大跌落,弹-脆-塑性模型较理想弹塑性模型可描述脆性软化后岩石的强度变化[25-26],上述研究中只有文献[14-15]使用了弹-脆-塑性模型.因此,本文基于统一强度理论和弹-脆-塑性模型,考虑中间主应力效应和脆性软化的共同影响,从侧压力系数小于1 出发,采用摄动法建立非静水压圆形隧道塑性区半径的解析解,给出所得解析解的适用范围,并与文献复变函数法、摄动法、数值模拟和总荷载不变法进行对比验证,最后探讨摄动参数、中间主应力和脆性软化对隧道塑性区形状与大小的影响规律.

1 基本理论

隧道开挖可简化为平面应变问题,遵循先加载后成洞规律.图1 为非静水压力下圆形隧道的平面应变力学模型,支护力pi均匀地作用在隧道洞壁处,无穷远处作用竖向地应力q.

图1 非静水压力下圆形隧道的力学模型Fig.1 Mechanical model of a circular tunnel under non-hydrostatic pressures

在图1 中,a为隧道半径,Rp为塑性区半径;r,θ分别为极坐标的半径和方位角,且θ以水平向右方向为起点、逆时针旋转为正;ε为摄动参数,侧压力系数λ=1 -ε,本文将从侧压力系数λ小于1 即0＜ε=1-λ＜1 出发,规定以压应力为正,并将无穷远处的水平/竖向地应力转换为径向/切向地应力,以采用极坐标求解非静水压力圆形隧道问题.

1.1 弹-脆-塑性模型和统一强度理论

岩土类材料的弹-脆-塑性模型如图2(a)所示[26],图中σ1为大主应力、σ3为小主应力,ε1为大主应变.弹-脆-塑性模型考虑了围岩峰后强度相比峰前有较大损失的脆性软化,较理想弹塑性模型更适合描述围岩峰后强度的真实变化.统一强度理论的 π 平面极限线如图2(b)所示[24],不同的统一强度理论参数b对应Mohr-Coulomb 强度准则(b=0)、双剪应力强度准则(b=1)以及一系列强度准则(0＜b＜1),以反映中间主应力σ2的不同影响程度.

图2 弹-脆-塑性模型和统一强度理论Fig.2 Elastic-brittle-plastic model and unified strength theory

采用黏聚力c和内摩擦角φ作为岩土材料强度参数时,以压应力为正的统一强度理论表达式为[27]

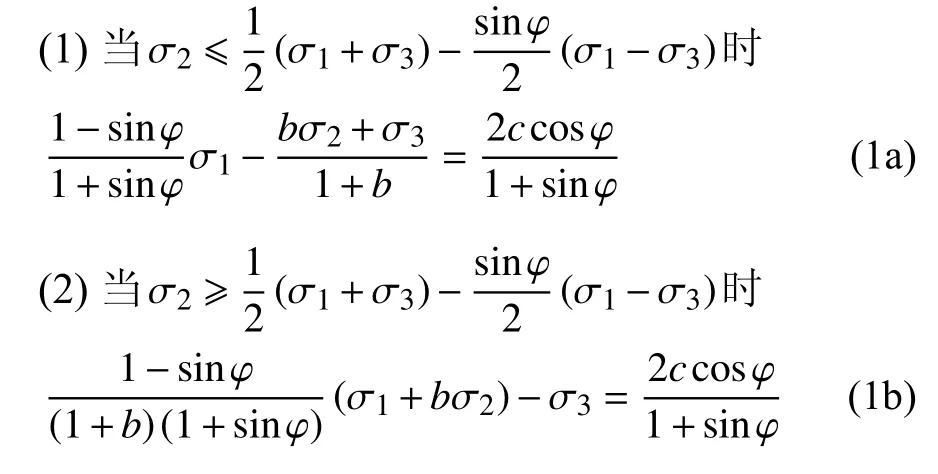
对于圆形隧道开挖平面应变问题,假设隧道纵向应力σz为中间主应力σ2且主应力之间的关系为[6,27-28]

因此,式(2)满足式(1b)的应力判定条件.将式(2)代入式(1b),整理得统一强度理论的平面应变表达式为

假设围岩为均匀、连续且各向同性的弹-脆-塑性材料,屈服时遵循统一强度理论,则由式(3)得隧道围岩峰前/峰后的强度准则为[28]

式(6)表示围岩主应力与极坐标应力分量之间的关系,其中σr,σθ,τrθ分别为非静水压力下围岩的径向正应力、切向正应力和切应力

将式(6)分别代入式(4)和式(5),得非静水压力下隧道围岩峰前/峰后的强度准则为

1.2 摄动法

对于非静水压力下圆形隧道的弹塑性非圆边界问题,摄动法将弹塑性非圆边界转化为数学微分方程,再根据无穷远处的应力边界逐阶求解.由应力坐标转换公式得无穷远处(+r面)的径向正应力σr|r→∞和切应力τrθ|r→∞为

图3 为摄动法求解非静水压力下圆形隧道塑性区半径的逐阶过程,洞壁处始终作用均匀支护力pi,无穷远处应力边界按摄动参数ε的阶数进行离散.首先求作用下即ε0阶问题的围岩弹性区应力和隧道塑性区半径,后续每个离散的应力边界在前一阶解答的基础上逐阶修正,最终获得εn阶问题的解答.

Φ是关于半径r和方位角θ的应力函数,式(10)为应力函数Φ(r,θ)需满足的相容方程

围岩弹性区应力可由应力函数Φ(r,θ)表示为

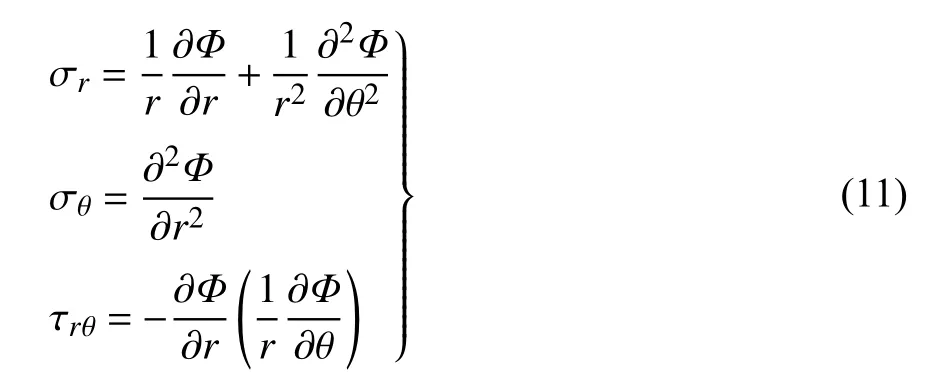
由图3 可知,围岩弹性区应力、隧道塑性区半径和应力函数均与无穷远处的应力边界有关,将这些量按摄动参数ε的阶数展开得其摄动解形式为

图3 摄动法逐阶求解Fig.3 Steps to apply the perturbation method

联立式(9)、式(12a)和式(12c),依据摄动参数ε各次项的系数相等得隧道无穷远处的应力边界为

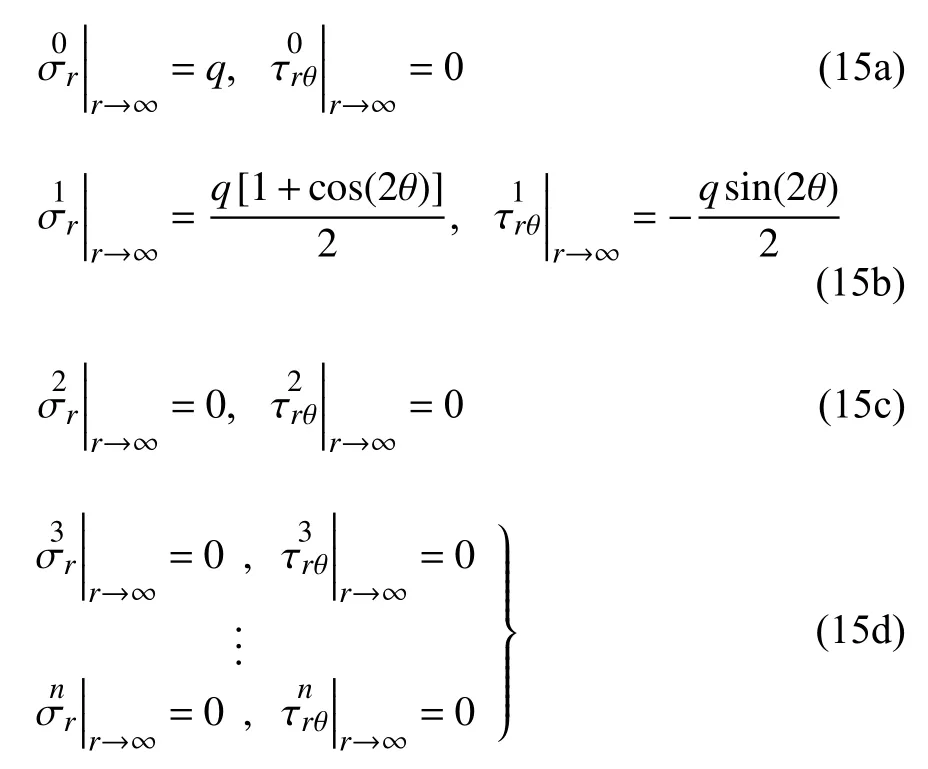
式(13)为摄动法求解非静水压力下圆形隧道塑性区半径Rp的表达式,可结合定解条件依次获得ε0阶塑性区半径R0,ε1阶塑性区半径R0[1-εR1(θ)](求R1(θ)),ε2阶塑性区半径R0[1-εR1(θ)-ε2R2(θ)](求R2(θ)),持续计算εn阶的塑性区半径(求Rn(θ),n≥3),相邻阶数间的结果相差满足精度时停止计算.

2 塑性区半径求解

2.1 塑性区应力

在非静水压力下圆形隧道的围岩塑性区内,平衡微分方程为

当塑性区完全包围隧道时,围岩塑性区应力只与隧道洞壁处的应力边界和几何形状有关[10-12,14-15,17-18],属于屈服方程和平衡微分方程联立求解的静定边值问题,且在围岩塑性区内σr＜σθ.由图1 可知,圆形隧道在r=a处σr=pi,τrθ=0,表明洞壁处的应力边界和几何形状均为绕轴对称,根据连续性条件得围岩塑性区的应力与方位角θ无关,其径向正应力σr和切向正应力σθ只与半径r有关,又因切应力τθr关于θ面反对称,则切应力τrθ(p)=τθr(p)≡0,进而在围岩塑性区内式(16b)恒成立,式(16a)变为

联立围岩峰后强度准则式(8)和平衡微分方程式(17),并结合τrθ(p)≡0 和隧道洞壁处的应力边界即定解条件r=a时σr=pi,得围岩塑性区应力为

式中,上标p 代表围岩塑性区、弹塑性交界线内侧.

对于弹-脆-塑性模型下隧道弹塑性交界线的内侧与外侧,围岩存在强度突变,塑性应力也产生了突变:弹塑性交界线的内侧属于塑性区,应力满足以围岩残余强度参数表达的峰后强度准则式(8),可令式(18)中r=Rp获得;弹塑性交界线的外侧属于塑性区也属于弹性区,应力满足以围岩初始强度参数表达的峰前强度准则式(7),联立式(7)、式(17)和沿着弹塑性交界线的法线方向应力连续、切线方向应力连续得外侧三个塑性应力分量为

式中,上标op 代表弹塑性交界线外侧.

因此,弹塑性交界线内侧与外侧上每点都处于绕轴对称的主应力状态,径向正应力、切向正应力可分别类比为岩石轴对称三轴压缩试验的围压和抗压强度,围压相同但抗压强度不同,进而在弹塑性交界线内侧与外侧的两个塑性应力分量连续(径向正应力、切应力),而切向塑性应力发生了突变.但在弹塑性交界线的外侧,三个应力分量的塑性值与弹性值均相等,将作为2.2 节中塑性区半径计算的定解条件之一.

2.2 塑性区半径

非静水压力下圆形隧道弹性区应力满足两个位置的应力边界,一是无穷远处,径向正应力与切应力收敛于式(15),二是弹塑性交界线的外侧,三个应力分量的塑性值与弹性值相等,也可转化为径向正应力与切应力两个分量连续再加应力弹性值满足围岩峰前强度准则,这两个位置的应力边界作为定解条件以获得塑性区半径的表达式.

2.2.1ε0阶问题

在图3(a)的ε0阶问题中,圆形隧道洞壁处作用均匀支护力pi,由式(15a)知无穷远处只作用均匀径向荷载q、无剪切荷载,属于侧压力系数λ=1 即静水压力下经典的隧道问题,相应ε0阶围岩弹性区应力为[28]

式(20)已满足的定解条件,包括无穷远处应力边界,弹塑性交界线外侧的围岩峰前强度准则、切应力塑性值与弹性值相等,再根据弹塑性交界线外侧径向正应力的塑性值与弹性值相等,即r=Rp=R0时式(19a)中的σr(op)等于式(20a)中的,得ε0阶隧道塑性区半径的摄动解析解为[28]

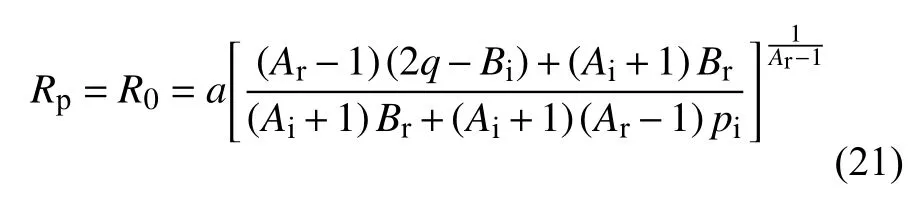
2.2.2ε1阶问题

在ε0阶围岩弹性区应力和隧道塑性区半径解析解的基础上,ε1阶问题的待求量有,R1(θ);式(15b)为ε1阶隧道无穷远处的应力边界,属于ε1阶问题的定解条件之一.

在ε1阶弹塑性交界线外侧r=Rp=R0[1-εR1(θ)]时的定解条件,包括式(22a)—径向正应力的塑性值和弹性值相等、式(22b)—切应力的塑性值和弹性值相等和式(22c)—应力弹性值满足围岩峰前强度准则

将式(22)在r=R0处按泰勒级数展开,根据展开式两边摄动参数ε一次项的系数相等并代入式(19a)、式(19c)和式(20),整理得

将ε1阶隧道无穷远和r=R0处的应力边界即式(15b)、式(23a)分离常数项、三角函数项后变为

由式(24)可知,ε1阶应力边界包括常数项和cos(2θ)或sin(2θ)项两部分,可设应力函数=g1(r)+g2(r)cos(2θ),代入相容方程式(10)并根据常数项和cos(2θ)项的系数分别等于0 得

另设r=et,则式(25)变为

可见,式(26)为两个独立的4 阶常系数齐次微分方程,式(26a)的特征根k1=k2=0,k3=k4=2,式(26b)的特征根k5=4,k6=2,k7=0,k8=-2,故式(26)的通解为

式中,A1,B1,C1,D1;A2,B2,C2,D2均为待定系数.

将式(28b)代入式(23b)得

将式(21)和式(29)代入Rp=R0[1-εR1(θ)],得ε1阶隧道塑性区半径的摄动解析解为

2.2.3εn阶问题

在ε1阶围岩弹性区应力和隧道塑性区半径解析解的基础上,ε2阶问题的待求量有,R2(θ).按2.2.2 节的分析思路求得

将式(21)、式(29)和式(32)代入Rp=R0·[1-εR1(θ)-ε2R2(θ)],得ε2阶隧道塑性区半径的摄动解析解为

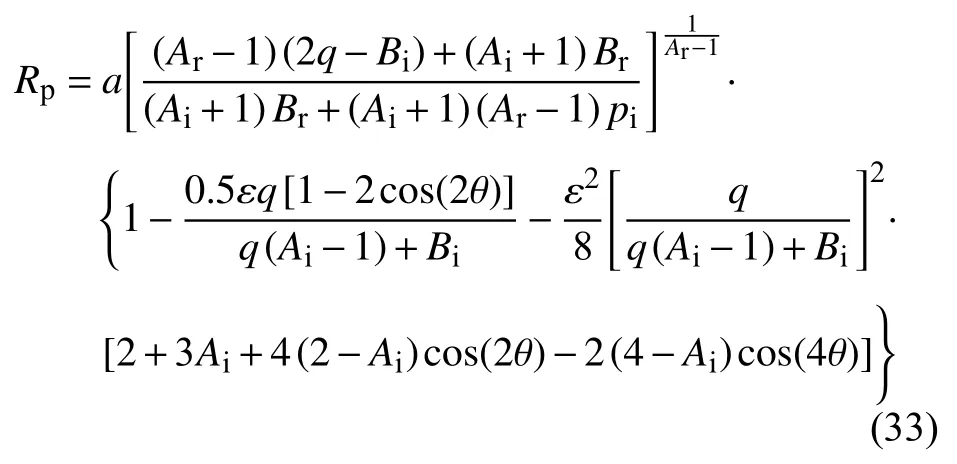
在ε2阶围岩弹性区应力和隧道塑性区半径解析解的基础上,ε3阶问题的待求量有,R3(θ).按2.2.2 节的分析思路求得

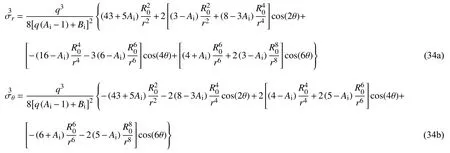
将式(21)、式(29)、式(32)和式(35)代入Rp=R0[1-εR1(θ)-ε2R2(θ)-ε3R3(θ)],得ε3阶隧道塑性区半径的摄动解析解为

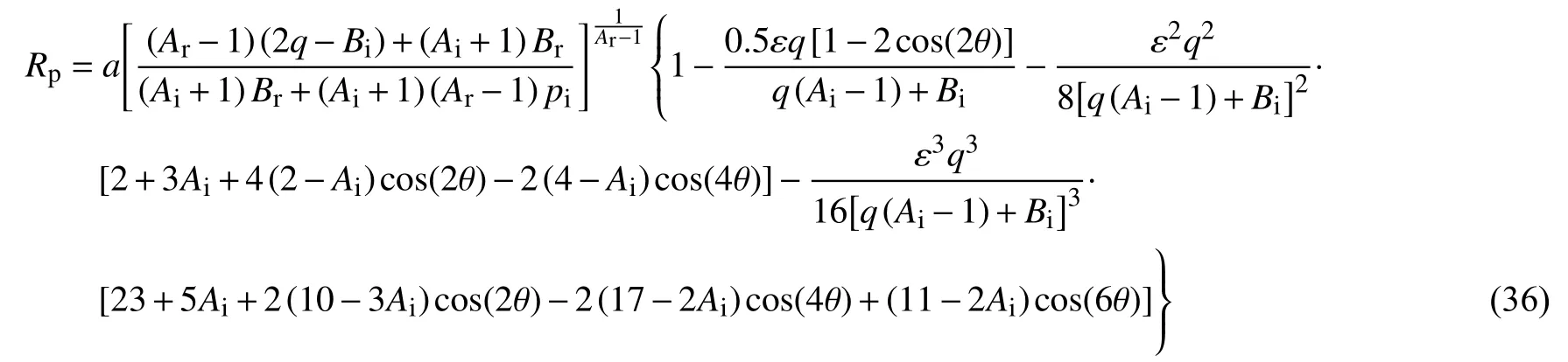
依次类推,可得到εn阶隧道塑性区半径的摄动解析解.本文基于统一强度理论所建立的非静水压圆形隧道塑性区半径的脆塑性摄动解析解,考虑了中间主应力效应和脆性软化的共同影响,包括Mohr-Coulomb 强度准则解答(b=0)[17-18]和反映中间主应力效应不同程度的系列强度准则解答(0＜b≤1),且理想弹塑性模型解答为其特例[17-18],具有重要理论意义和良好工程应用前景.

2.3 摄动阶数

随着摄动阶数n的提高,非静水压力下隧道塑性区半径的解析表达式越复杂,有必要在保证精度的前提下尽可能降低摄动阶数.取文献[29]中的隧道算例,弹-脆-塑性围岩强度参数ci=1.8 MPa,φi=45°,cr=0.7 MPa,φr=32°,理想弹塑性围岩强度参数cr=ci=1.8 MPa,φr=φi=45°.图4 为ε0阶、ε1阶和ε2阶隧道塑性区边界线的对比,其中a=3 m,pi=0.5 MPa,q=30 MPa,ε=0.3 对应λ=0.7,b=0,0.5,1.

由图4 可以看出,对于所取的隧道算例,无论是不同的材料模型还是不同的统一强度理论参数b,ε2阶隧道塑性区边界线与ε0阶的圆形相差明显,但相比ε1阶的变化很小,且ε3阶与ε2阶的塑性区边界线基本重合(图4 中未给出ε3阶),故ε2阶摄动解既满足精度又表达较简洁,下文设定统一取到ε2阶.

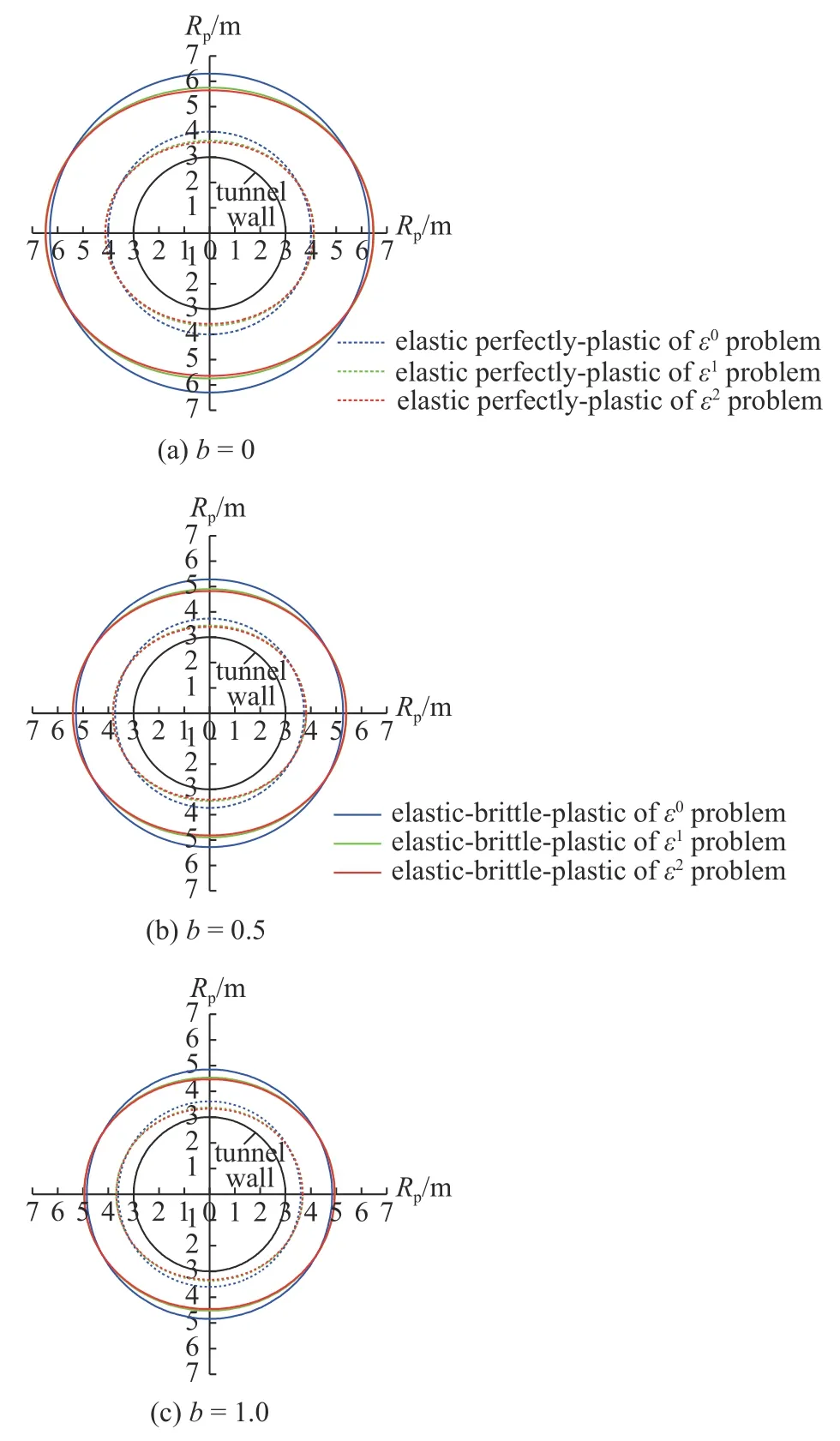
图4 ε0 阶、ε1 阶和ε2 阶塑性区边界线的对比Fig.4 Comparison of plastic boundary for the ε0,ε1 and ε2 problems

此外,两种材料模型下隧道塑性区均为双轴对称的类椭圆,可只比较第I 象限的塑性区形状和大小;弹-脆-塑性模型下隧道塑性区范围相比理想弹塑性模型下的要大得多,b=0,0.5,1 时理想弹塑性模型ε2阶类椭圆塑性区的长/短轴分别相差0.52,0.41,0.36 m,相应弹-脆-塑性模型的分别相差0.82,0.58,0.48 m;统一强度理论参数b对隧道塑性区范围的影响显著而对塑性区形状的影响较小,且b=0 时的隧道塑性区范围最大,于是在4.1 节和4.3 节中仅讨论b=0.

图5 为弹-脆-塑性模型下ε2阶隧道弹塑性交界线内侧塑性应力与外侧弹性应力在第I 象限的分布情况,未标出为零的切应力.可以看出,径向正应力在弹塑性交界线处连续,而切向正应力的外侧弹性值高于内侧塑性值,满足定解条件和脆塑性强度的要求;同理,可图示验证在弹塑性交界线外侧三个应力分量的弹性值与塑性值相等.

图5 弹塑性交界线处的应力分布Fig.5 Stress distribution at the elastic-plastic boundary

2.4 适用范围

对于非静水压力下圆形隧道的弹塑性分析,根据洞周围岩是否屈服分为三种情况:纯弹性状态、洞周部分围岩屈服、洞周围岩全部屈服,对应隧道无塑性区、塑性区局部包围隧道和塑性区完全包围隧道.以侧压力系数λ小于1 即0＜ε＜1 为例,先假定塑性区完全包围隧道,此时类椭圆塑性区的长轴位于θ=0°处、短轴位于θ=90°处,将θ=0°和90°代入式(33)并记为Rp(θ=0°)和Rp(θ=90°),再探讨三种屈服情况的判别.

若Rp(θ=90°)≥a,则塑性区完全包围隧道,本文摄动解析解适用于求解此情况下隧道的塑性区半径和弹性区应力分布.

若Rp(θ=0°)≥a但Rp(θ=90°)＜a,则塑性区局部包围隧道,本文摄动解析解不适用这种情况.根据塑性区边界线与隧道洞壁相交可求出塑性区的范围,令Rp=a代入式(33)以确定塑性区边界线与隧道洞壁的交点.

取文献[30]中的理想弹塑性软岩隧道算例:a=1 m,pi=0 MPa,q=1 MPa,ε=0.2 对应λ=0.8,cr=ci=0.276 MPa,φr=φi=35°,b=0,0.5,1.图6为按2.2 节求得的隧道塑性区边界线,其中b=0,0.5 时塑性区完全包围隧道,b=1 时塑性区局部包围隧道、塑性区边界线与隧道洞壁相交于A点,仅能从A点估算塑性区范围.

图6 塑性区边界线的确定Fig.6 Determination of plastic boundary

若Rp(θ=0°)＜a,则隧道处于纯弹性状态,由基尔希公式求围岩应力分布.

此外,摄动参数ε可依据隧道所处地应力场即ε=1-λ确定,并按照上述思路判定本文摄动解析解的适用性;同时,摄动参数ε越小越好,建议侧压力系数λ＜1 时摄动参数ε＜0.5.

3 对比验证

为验证本文非静水压力下圆形隧道塑性区半径摄动解析解的正确性和合理性,分别与文献复变函数法、摄动法、数值模拟和总荷载不变法的结果进行比较,并探讨摄动参数ε的取值范围.需要说明的是,这4 种方法均基于Mohr-Coulomb 强度准则,对应本文的统一强度理论参数b=0,除总荷载不变法采用弹-脆-塑性模型以外都假定围岩符合理想弹塑性模型即cr=ci,φr=φi.

3.1 复变函数法

吕爱钟等[10]建立了非静水压力下圆形隧道塑性区半径的复变函数解答.取文献[10]中的隧道算例:a=2 m,pi=0 MPa,q=15 MPa,cr=ci=1 MPa,φr=φi=30°,ε=0.1,0.2,0.3 分别对应λ=0.9,0.8,0.7.图7 中本文与文献[10]的隧道塑性区边界线吻合良好,验证了本文解析解的合理性,且随着侧压力系数λ趋近于1,两种方法的结果差异在减小;Kastner 法忽略围岩弹塑性发展过程,较本文摄动法低估塑性区范围0.77～1.89 m.

图7 对比复变函数法的塑性区边界线Fig.7 Comparisons with the plastic boundary of the complex variable function method

3.2 摄动法

魏悦广[17]从侧压力系数λ＞1 出发,推导了非静水压力下圆形隧道塑性区半径的摄动解答.取文献[17]中的两组隧道算例:(1)a=1 m,pi=0 MPa,q=13.1 MPa,cr=ci=2.45 MPa,φr=φi=30°,ε=-0.125 对应λ=1.125;(2)a=1 m,pi=0 MPa,q=24.5 MPa,cr=ci=2.45 MPa,φr=φi=30°,ε=-0.2 对应λ=1.2.本文隧道塑性区边界线与文献[17]的完全吻合,如图8 所示,证明了本文解析解的正确性,同时得出:本文解析解适用于侧压力系数大于1 的情况,表明摄动参数ε＜0 是可行的.

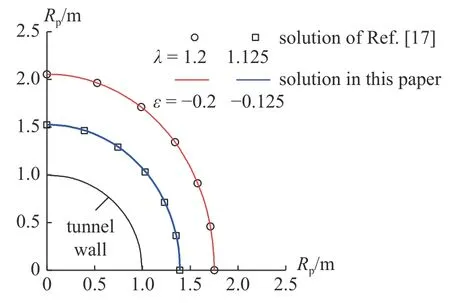
图8 两种摄动解答的对比Fig.8 Comparisons of two perturbation solutions

3.3 数值模拟

Bagheri 等[16]采用二维弹塑性有限元程序,开展了非静水压力下圆形隧道塑性区半径的数值模拟,拟合出参数d以描述4 种埋深下隧道塑性区半径的变化,其中d=Rp(ε≠0)/Rp(ε=0)代表非静水压力下与静水压力下圆形隧道塑性区半径的比值.取文献[16]中的隧道算例:pi=0 MPa,cr=ci=0.55 MPa,φr=φi=24°.本文摄动法参数d与文献[16]的数值模拟基本吻合,如图9 所示,同样证明了本文解析解的合理性,同时得出:本文解析解在侧压力系数λ小于1 和大于1 时均适用.

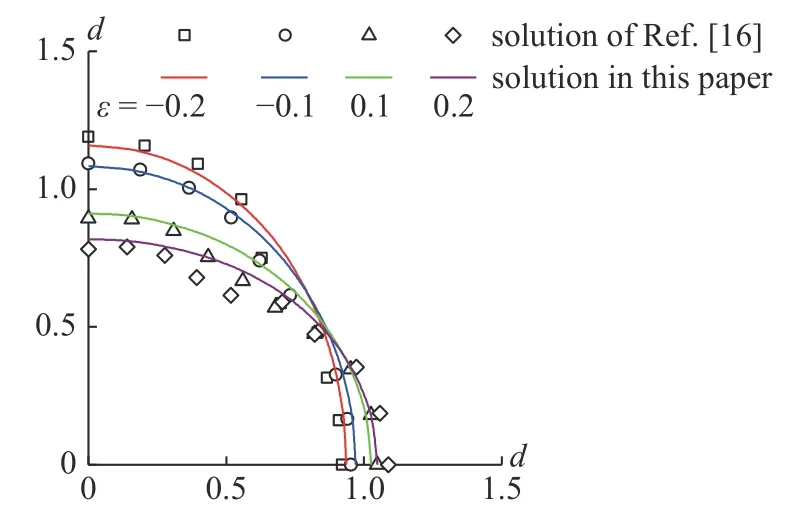
图9 不同ε 下参数d 的比较Fig.9 Comparisons of the parameter d with different ε

3.4 总荷载不变法

董海龙和高全臣[14]获得了非静水压力下圆形隧道塑性区半径的总荷载不变法解答.取2.3 节中的弹-脆-塑性隧道算例,ε=0.1,0.2,0.3 分别对应λ=0.9,0.8,0.7.图10 中两种方法的隧道塑性区边界线吻合较好,表明了本文解析解在弹-脆-塑性模型下的有效性.

图10 对比总荷载不变法的塑性区边界线Fig.10 Comparisons with the plastic boundary of the constant assumption of total loads

4 参数分析

4.1 摄动参数

隧道算例与2.3 节相同,图11 为不同摄动参数ε下两种材料模型的隧道塑性区边界线变化.可以看出,随着ε增加隧道塑性区边界线沿竖直向下移动、沿水平向右移动,且竖直方向上的变化更为明显.另外,对比图11(a)和图11(b)知,弹-脆-塑性模型的塑性区范围较理想弹塑性模型的明显增大、受摄动参数ε的影响与变化也更显著,表明理想弹塑性模型所得隧道塑性区范围较小(相差2.05～2.46 m),工程中宜采用弹-脆-塑性模型.

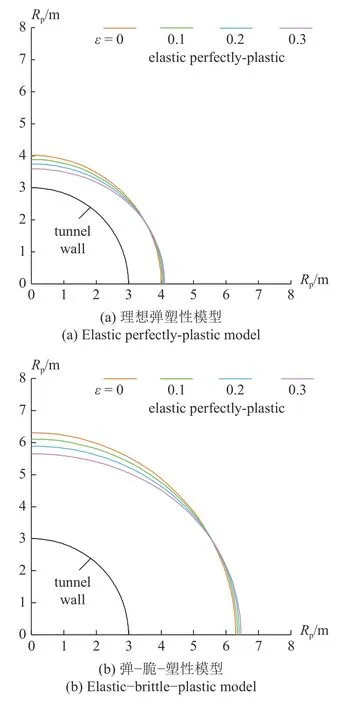
图11 不同ε 下塑性区边界线Fig.11 Plastic boundary with different ε

4.2 中间主应力

隧道算例与2.3 节相同,图12 为不同统一强度理论参数b下两种材料模型的隧道塑性区边界线变化.可以看出,随着参数b即中间主应力影响程度的增加,隧道塑性区范围在不断减小,体现了中间主应力对围岩强度的提高作用,尤其是弹-脆-塑性模型;Mohr-Coulomb 强度准则(图2(b)中b=0),相比b等于0.5 或1 没有利用围岩的强度潜能,理想弹塑性模型下b=0 时塑性区长轴较b=0.5,1 时增大了0.30,0.43 m,弹-脆-塑性模型下b=0 时塑性区长轴较b=0.5,1 时增大了1.07,1.52 m.

图12 不同b 下塑性区边界线Fig.12 Plastic boundary with different b

4.3 脆性软化

取文献[30]中的隧道算例:a=1 m,pi=0 MPa,q=1 MPa,b=0,ε=0.3 对应λ=0.7;软岩的弹-脆-塑性强度参数ci=0.276 MPa,φi=35°,cr=0.055 MPa,φr=30°,理想弹塑性强度参数cr=ci=0.276 MPa,φr=φi=35°;硬岩的弹-脆-塑性强度参数ci=0.173 MPa,φi=55°,cr=0.061 MPa,φr=52°,理想弹塑性强度参数cr=ci=0.173 MPa,φr=φi=55°.图13 为不同围岩类别下隧道的塑性区边界线变化,表明两种材料模型下软岩隧道的塑性区范围差异较硬岩隧道的显著(仅限于所取文献算例).

图13 不同围岩类别下塑性区边界线Fig.13 Plastic boundary for different rock masses

图14 为脆性软化即围岩峰后强度参数对软岩隧道塑性区边界线的影响,硬岩隧道亦然.可以看出,脆性软化幅度越大即围岩的峰后强度参数越小,塑性区边界线越大:峰后黏聚力cr平均每减小0.01 MPa,塑性区长轴增加0.09 m、短轴增加0.07 m;峰后内摩擦角φr平均每减小1°,塑性区长轴增加0.06 m、短轴增加0.05 m.

图14 峰后强度参数对软岩隧道塑性区边界线的影响Fig.14 Effect of post-peak strength parameter on the plastic boundary of soft rock tunnel

5 结论

(1)基于统一强度理论所建立的非静水压圆形隧道塑性区半径的脆塑性摄动解析解,合理考虑了围岩强度的中间主应力效应和脆性软化,可得到Mohr-Coulomb 强度准则解答和反映中间主应力效应不同程度的系列强度准则解答,能获得真实地应力场下较为准确的非圆塑性区边界线,将有效指导以收敛约束法为基础的隧道支护选型和刚度设计,具有重要理论意义和良好工程应用前景.

(2)对比文献复变函数法、摄动法、数值模拟和总荷载不变法,验证了本文隧道塑性区半径摄动解析解的正确性和合理性,亦表明摄动参数可正可负,并根据围岩屈服情况给出所得解析解的适用范围.摄动参数对隧道类椭圆形塑性区的大小和长/短轴变化都有明显影响,且竖直方向上的塑性区变化更为突出.

(3)随着中间主应力效应的增加,隧道的塑性区范围显著减小,Mohr-Coulomb 强度准则解答的塑性区范围最大而偏保守,尤其是弹-脆-塑性围岩.围岩峰后强度越低则隧道的塑性区范围越大,理想弹塑性模型忽略围岩峰后强度跌落相比弹-脆-塑性模型得到的塑性区偏小.