基于Triplet Network的小样本轴承、齿轮故障诊断方法*

谢由生,张 军

(安徽理工大学 人工智能学院,安徽 淮南 232001)

0 引 言

作为现代工业中的关键设备,智能机械设备在电力、航空和工业生产等众多领域发挥着至关重要的作用。

但是智能机械设备中的典型部件,如轴承、齿轮的故障,严重威胁着智能机械设备的安全、可靠运行。故障诊断是确保这些智能机械设备长期、稳定运行的重要手段之一[1]。

近些年,随着深度学习在自然语言处理(natural language processing, NLP)[2]、计算机视觉(computer vision,CV)[3]等领域取得的重大成功,众多学者把深度学习方法应用到机械设备故障诊断中,并取得了一定的成果。

CHEN L等人[4]提出了一种非线性频谱与堆栈降噪自编码相结合的方法,采用该方法对永磁同步电机进行故障诊断时,取得了较高的诊断准确率。KONG X等人[5]使用了基于深度自编码器的多集成方法,用于轴承的故障诊断,取得了较好的诊断精度,并且该方法还具有较强的泛化能力。ZARE S等人[6]提出了一种基于多通道卷积神经网络的故障诊断方法,采用该方法可以较好地对风力发电机的常见故障进行诊断。赵凯辉等人[7]采用Inception模型和双向长短时记忆模型(bi-directional long short-term memory,Bi-LSTM)相结合的方法,在多负载下的轴承故障诊断中取得了较好的结果,且该方法的抗干扰能力较强。

这些基于深度神经网络的故障诊断方法极大地提高了故障诊断的精度,但是这些方法的高准确率往往依赖大量的故障样本来训练模型。而在实际的生产活动中,想要获得充足的故障样本,需要花费大量的人力和物力。因此,针对小样本条件下的故障诊断是当前故障诊断领域的一大挑战。

面对小样本下故障诊断精度不高的问题,不少学者提出了解决方法。

SHAO S等人[8]提出了一种基于辅助分类器生成对抗网络模型(auxiliary classifier generative adversarial networks, ACGAN),用以学习真实的原始数据特征;该模型通过学习的特征,生成带有标签的伪故障样本,用来填充真实的小样本故障数据。LUO J等人[9]结合了深度卷积网络、条件生成对抗网络(conditionalgenerative adversarial networks, CGAN)这二者的优点,提出了一种条件深度卷积对抗网络模型,用于生成故障样本,对小样本故障数据集进行数据增强。HAN H等人[10]将生成对抗网络和层叠自动编码器相结合,首先利用生成对抗网络对小样本数据进行了增强,然后使用层叠自动编码器提取信号的特征,在对给水泵故障进行诊断时取得了较好的结果。LIU S等人[11]开发了一种LOSGAN(latent optimized stable GAN)模型,在没有先验知识的情况下,自适应地增强小样本数据,并且使用分布差异距离来约束模型的优化目标,采用自注意力和谱归一化来稳定训练过程,在小样本轴承故障诊断中表现出了较优的性能。马波等人[12]将健康状态数据反映的设备个性特征和故障机理反映的设备共性特征相结合,提出了一种基于GAN理论的模型,用于生成样本,对小样本故障数据进行了数据增强。

综上所述,现有提高小样本故障诊断精度的方法,多是先采用生成对抗网络生成伪样本,再对小样本故障数据进行数据增强。但是,训练一个优秀的生成对抗模型同样需要大量的样本,在实际的小样本故障诊断中存在一定的局限性。

因此,笔者提出一种基于Triplet Network[13]的故障诊断方法,即首先将原始故障信号转换为二维时频信号,然后对比时频信号故障样本特征的相似度,以此来改善模型提取的特征,最后通过比较未知样本与已知样本特征的相似度,实现对未知样本的故障识别。

1 模型结构与故障诊断流程

由于传统的深度学习模型很难从有限的故障样本中学习到故障的特征,基于此训练出来的模型往往是欠拟合的,故障诊断的效果较差。

笔者提出一种基于Triplet Network的方法,用于提高小样本故障诊断精度。

基于Triplet Network方法的结构图如图1所示。

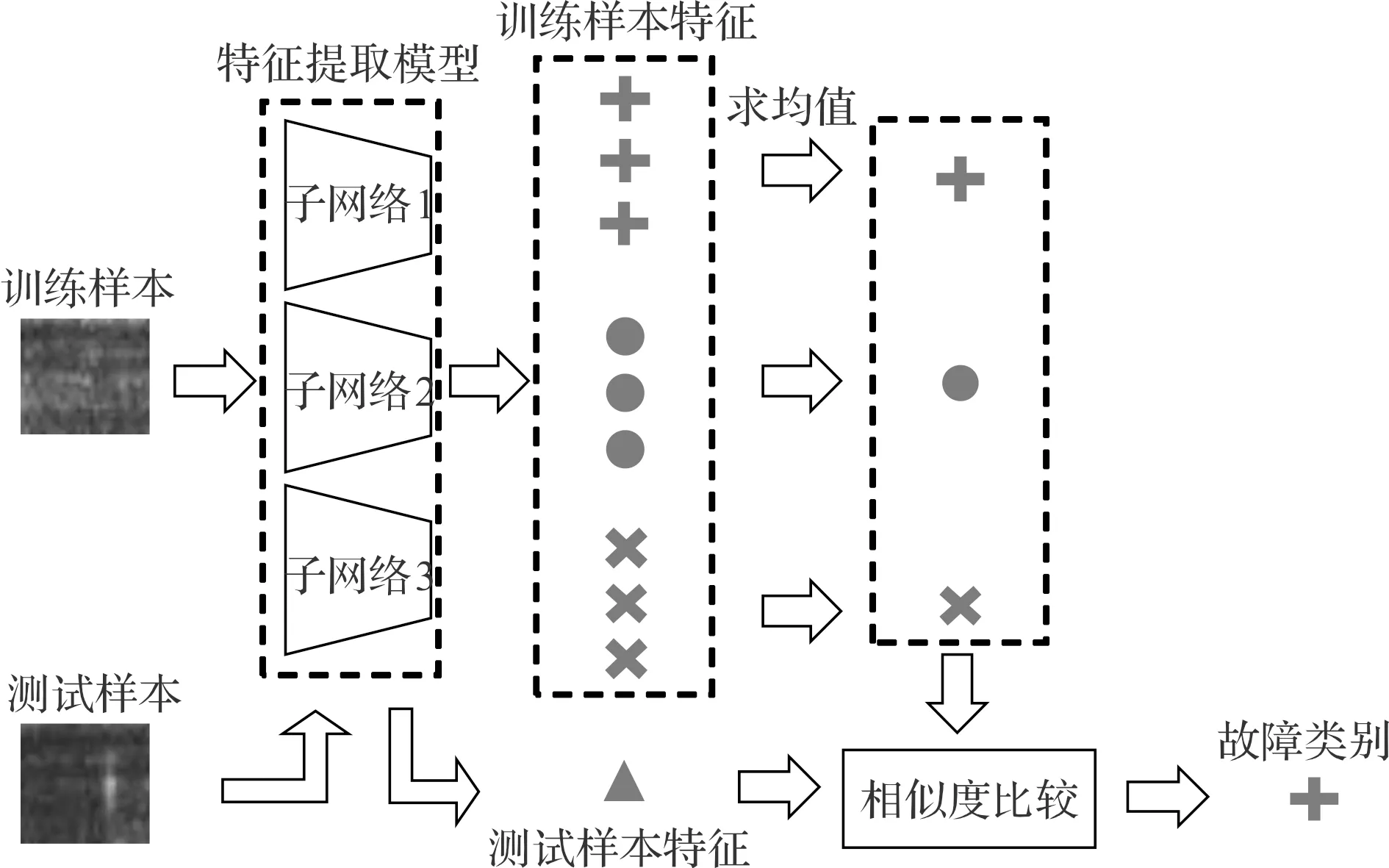
图1 基于Triplet Network的方法结构图

1.1 特征提取模型

借鉴Triplet Network模型的思想,特征提取模型构建了一个具有3个共享权值的子网络模型,通过提取同一故障状态样本间和不同故障状态样本间的特征,通过度量相同和不同故障状态样本特征的相似度,以此来优化模型抽取的特征,进而实现对不同故障的甄别。

特征提取模型结构如图2所示。

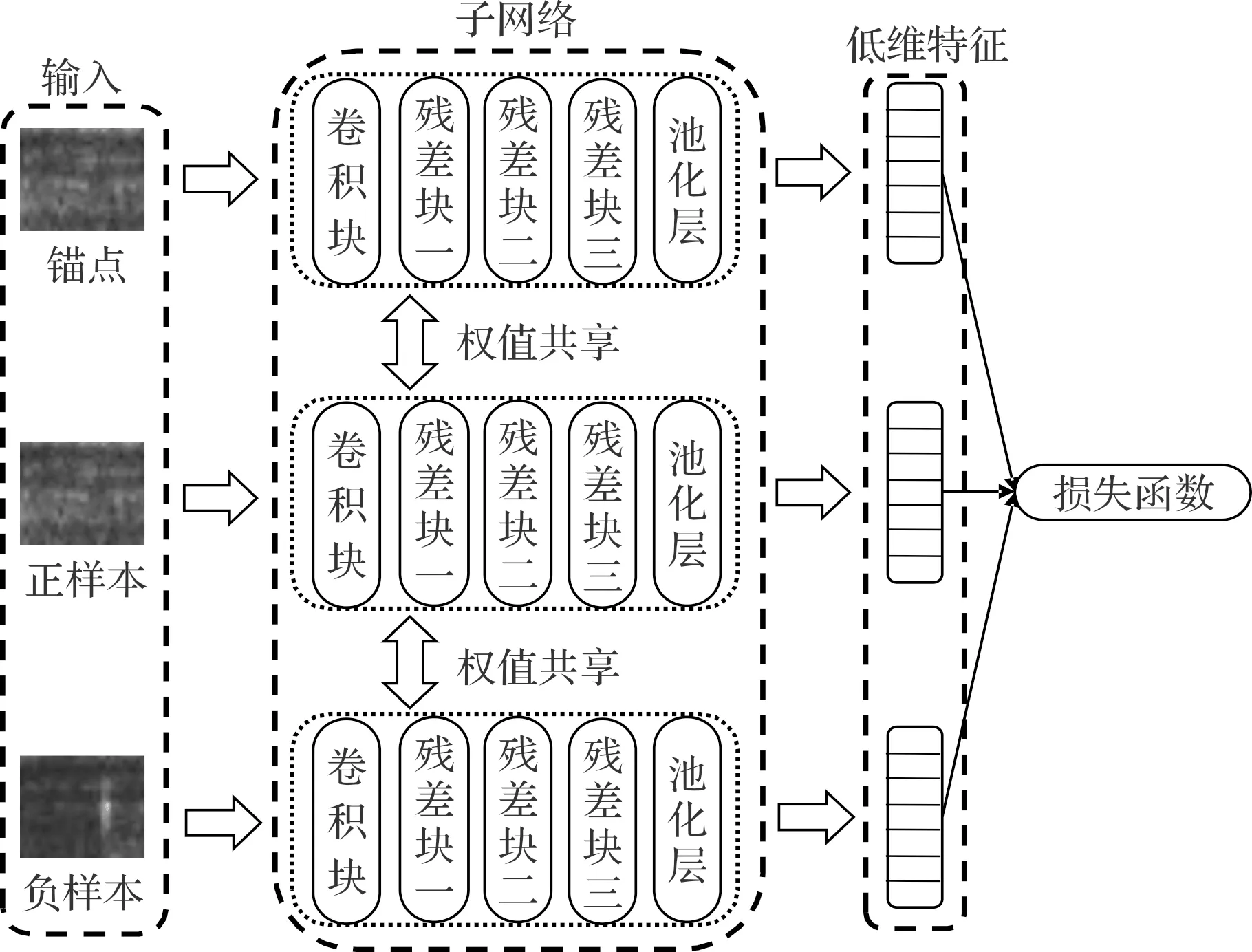
图2 特征提取模型结构

图2中,模型的输入是锚点、正样本和负样本组成的样本对;锚点是从故障样本中随机选取的一个样本,正样本是与锚点同一故障状态的样本,负样本是与锚点不同故障状态的样本;输出是样本对低维特征向量间的相似度度量,即损失值;损失值通过反向传播更新模型的参数,优化模型学习的故障样本类内和类间特征,使模型提取的锚点与正样本低维特征向量的相似度越来越高,锚点与负样本低维特征向量的相似度越来越低。

模型的子网络中包含1个卷积块、3个残差块和1个池化层,通过这些模块组成的模型,实现样本对低维特征的提取。

1.1.1 卷积块

模型的卷积块由卷积层、批归一化层、激活函数和池化层构成。

卷积层。卷积计算是现在深度神经网络的主要组成部分,卷积可以有效地提取输入对象的特征,因此也称为特征提取层。卷积中的卷积核每次提取的特征是输入对象的局部特征,但是卷积核通过滑动遍历整个输入对象,实现对整个对象的特征提取。卷积核的大小由人为设置,卷积核中的参数由梯度反向传播自动更新,解决了人工设置的繁琐。

卷积计算可以表示为:

Xi=Wi*Xi-1+bi

(1)

式中：*—卷积运算；Wi—第i层的卷积核；bi—第i层的偏置值；Xi-1—第i-1层的输出特征。

批归一化层。在模型训练过程中，参数一直处于变化状态，模型中间层的数据分布变化较大。IOFFE S等人[14]提出了批归一化方法，在模型中间层对数据进行归一化处理。批归一化可以改善模型反向传播时的梯度爆炸或梯度消失问题，同时也可以起到正则化作用，一定程度上缓解了模型的过拟合现象。

激活函数。激活函数将非线性因素引入神经网络中，使神经网络可以逼近任意非线性函数。在提高模型的表示能力和学习能力上，激活函数起到了至关重要的作用。常用的激活函数有Sigmoid函数、Tanh函数和ReLU函数等，笔者所提模型使用的激活函数有ReLU函数和Sigmoid函数。

激活函数的表达式为：

(2)

(3)

池化层。池化层对输入对象进行特征选择，降低输入对象的维度，可以大幅度地减少模型参数数据，在避免模型过拟合上有一定效果。

笔者所提模型的卷积块中采用最大池化层，残差块后的池化层为平均池化层。池化层可以表示为：

y=Pool(xi)(i=1,2,…,d)

(4)

式中：y—输出；xi—输入对象的第i个区域。

其中：最大池化层的Pool(·)为max(·)，即取该区域中的最大值；平均池化层的Pool(·)为mean(·)，即取该区域的平均值。

1.1.2 残差块

2016年,HE K[15]提出了深度残差网络(deep residual network, ResNet),ResNet模型在构建深度神经网络上取得了巨大成功。

笔者将ResNet模型中的残差结构引入到模型中,残差块结构如图3所示。

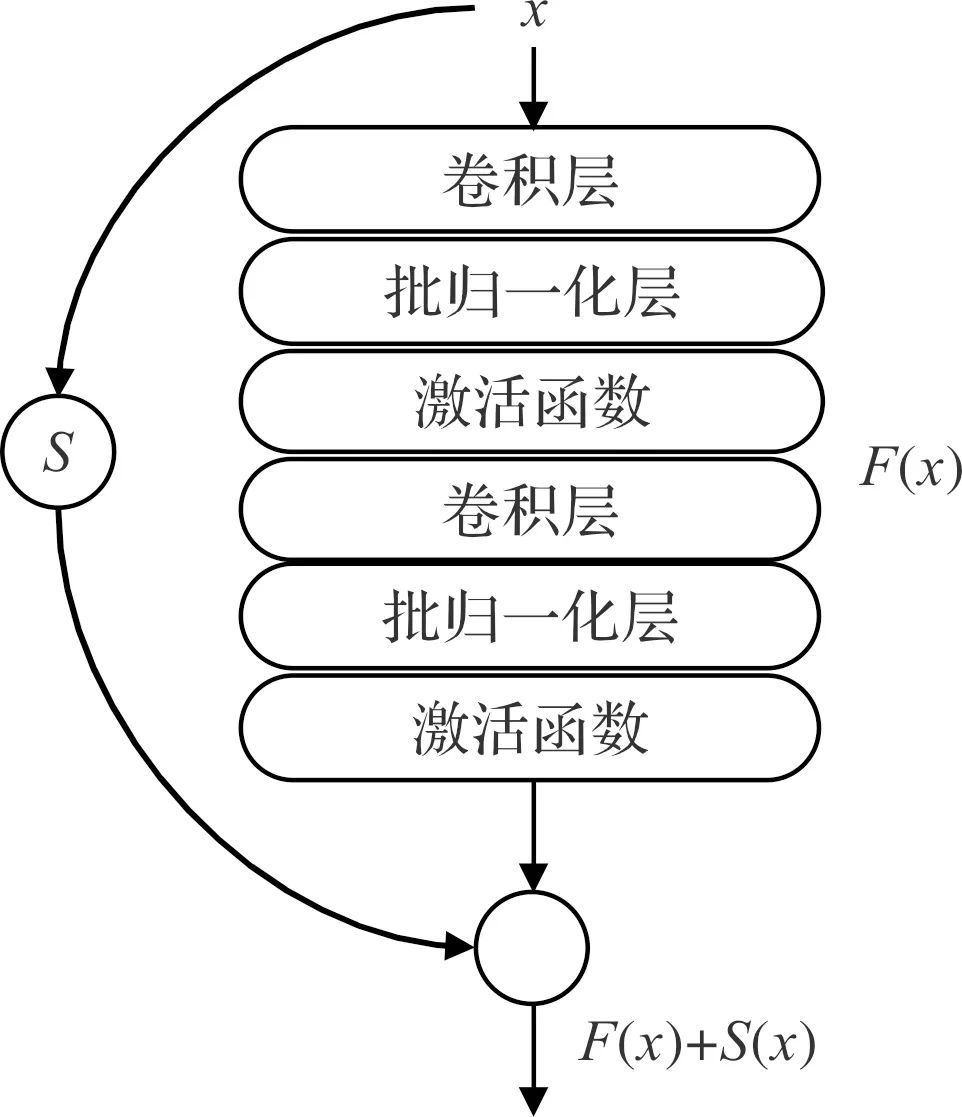
图3 残差结构

图3中，输入x需要经过主线和支线，其中，主线由两个卷积层、批归一化层和激活函数组成；

此处x经过主线表示为F(x)；输入x经过支线可表示为S(x)，S(·)进行何种计算需要根据该残差块中输入x与F(x)的维度决定，若x与F(x)的维度相同，则S(·)不进行任何操作，直接将输入x输出；若x与F(x)维度不相同，则S(·)为卷积核为1的卷积层，对输入x进行维度调整，使S(x)的维度与F(x)的维度保持一致；

输入x经过主线和支线后，将输出S(x)和F(x)相加，然后再作为后期操作的输入。

残差块可以表示为：

R(x)=F(x)+S(x)

(5)

1.1.3 损失函数

笔者所提模型的损失函数是度量锚点、负样本和正样本低维特征间的相似度，指导模型的优化方向，使模型提取的锚点与正样本低维特征向量的相似度越来越高，锚点与负样本的低维特征向量的相似度越来越低。

损失函数如下：

Loss=max(D(a,p)-D(a,n)+margin,0)

(6)

式中：a—锚点的低维特征；p—正样本的低维特征；n—负样本的低维特征；D(·)—衡量低维样本间的距离。

笔者使用的是欧式距离，距离越小相似度越高；margin是人为设定的阈值，控制模型的优化进程，若D(a,p)+margin>D(a,n)，则模型继续优化，否则模型停止优化。

特征提取模型的具体结构和参数如表1所示。

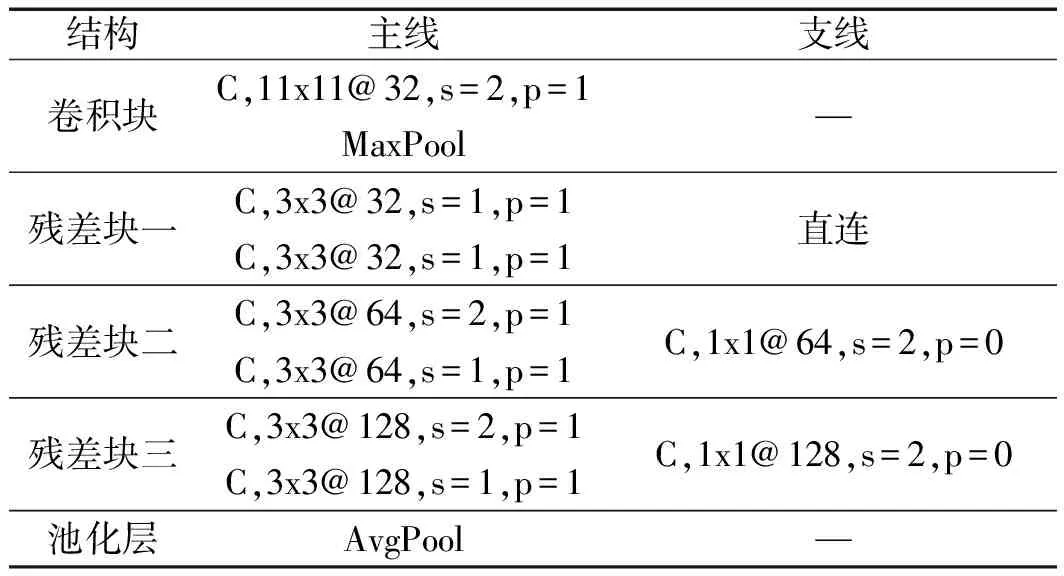
表1 模型详细结构参数

模型采用的是自适应平均池化,输出为1x1@128;支线中的直连为不进行操作,直接输出。模型中每个卷积计算后均加有批归一化和激活函数,激活函数为ReLU函数,平均池化层后的激活函数为Sigmoid函数。

1.2 故障诊断流程

模型故障诊断流程如图4所示。

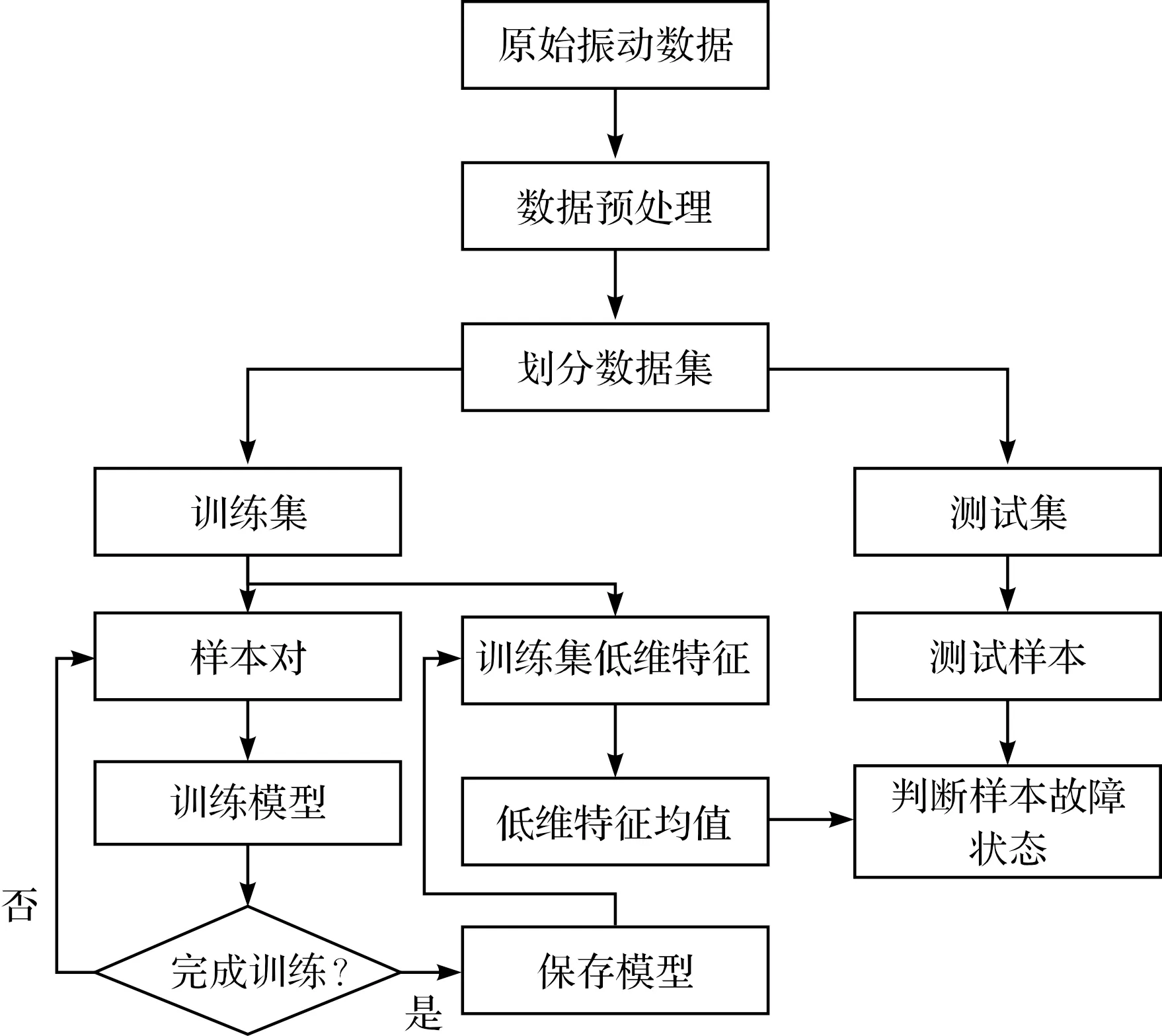
图4 故障诊断流程

图4中,诊断流程分为3个部分:数据预处理与数据集划分、训练模型、未知样本故障诊断。

(1)数据预处理与数据集划分。笔者所提模型的输入为二维数据,训练模型前需要将原始一维数据转换为二维数据。笔者采用短时傅里叶变换,将原始时序信号转换为时频信号,并将其保存为图片,取原始时序信号中1 024个点转换为一张时频信号图,依次选择样本点,并将其转换为时频图,直至转换结束。

划分数据集时,按时间顺序将样本划分为训练集和测试集,如图5所示;

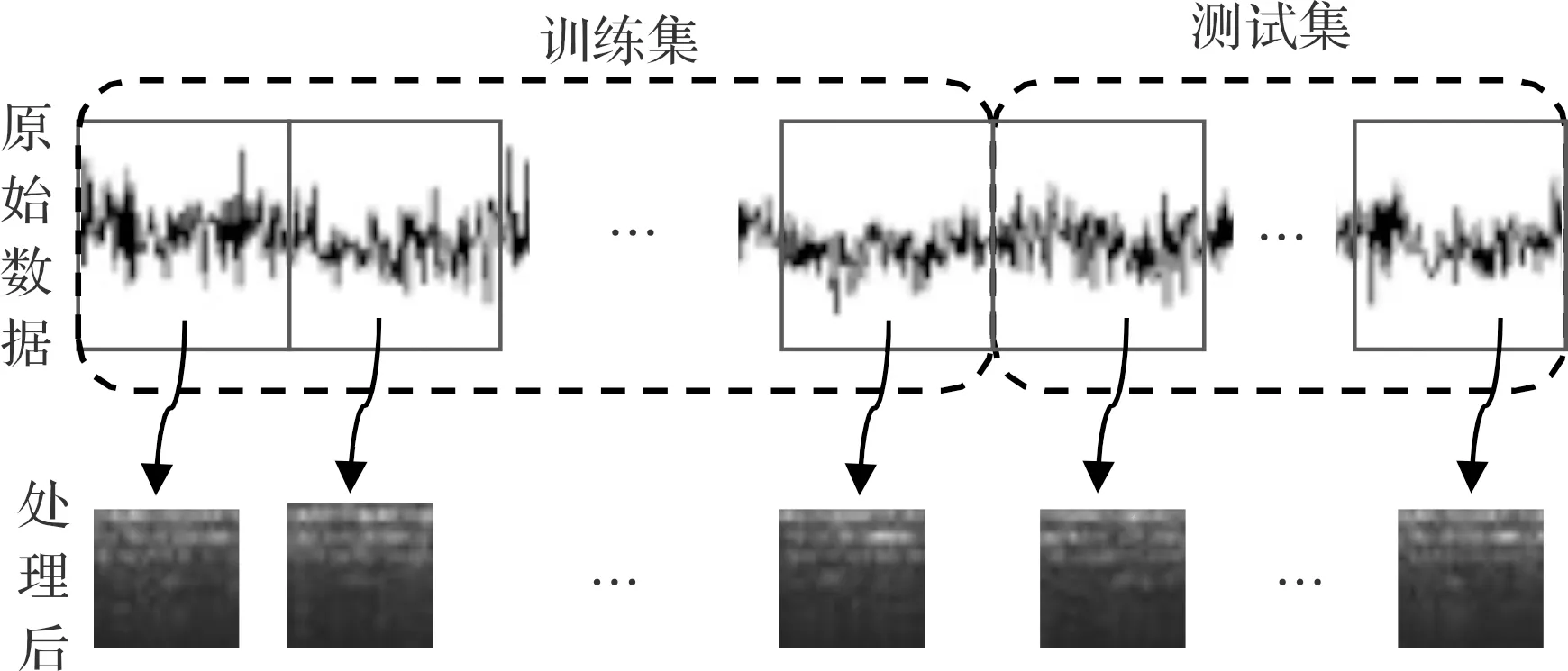
图5 数据预处理与数据集划分

(2)训练模型。从训练集中随机选择一个样本作为锚点,随机选择一个与锚点具有相同故障状态的样本作为正样本,随机选择一个与锚点具有不同故障状态的样本作为负样本。锚点、负样本和正样本组成的样本对输入模型得到损失值,损失值经过梯度反向传播优化模型参数。如此迭代一定次数,并保存训练完成的模型;

(3)未知样本故障诊断。使用训练好的模型将训练集中各类故障样本转化为低维特征,并求各类故障样本低维特征的均值。

未知样本故障诊断如图6所示。

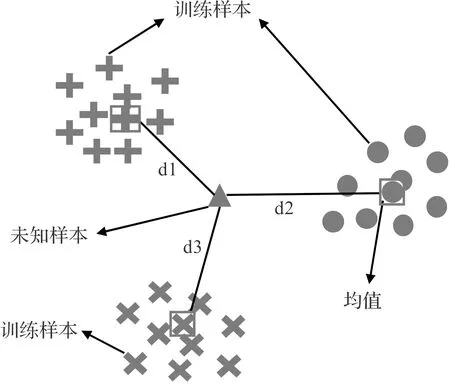
图6 未知样本故障诊断

图6中,当诊断未知样本故障状态时,对比未知样本的低维特征到各类故障样本低维特征均值的距离,距离最小者,则判定未知样本为该类。使用欧式距离测量样本间低维特征的距离。

2 实验与结果分析

笔者使用江南大学轴承数据集和美国康涅狄格大学齿轮数据集,测试模型在小样本情况下的故障诊断性能。

2.1 轴承数据

江南大学轴承数据集[16]有4种故障状态:健康、内圈故障、外圈故障和滚动体故障。振动信号的采集频率为50 kHz,在转速600 r/min、800 r/min和1 000 r/min下分别采集轴承的故障信号。将转速为800 r/min的轴承信号进行预处理和划分数据集(预处理和划分数据集方式见第1.2节)。

各类故障划分数据集的结果如表2所示。

表2 轴承数据集划分结果

2.1.1margin值的选择

margin作为一个人为设定的阈值,它决定了模型是否继续优化,当故障样本的类间距离小于故障样本的类内距离加margin的和时,模型需要继续优化;相反,则模型停止优化。由于故障样本的类内距离小于类间距离时,模型才能做出正确的判断,所以margin值应该大于0。但是,margin值并不是越大越好,当模型可以分辨不同故障时,若再拉远不同故障类间的距离,模型的故障诊断精度不会提高。

因此,笔者在0到1之间取了多个margin值,测试margin取值对故障诊断精度的影响;从训练集中选取各类故障30个样本作为本实验训练集,以表2中的测试集作为测试样本,计算模型故障诊断精度;

训练的学习率为0.01,每批次64个样本,优化器为Adam,并且采用学习率衰减策略动态调整学习率大小,总共迭代40次,并且重复实验5次,取其平均值。

margin值对故障诊断的影响实验结果如图7所示。

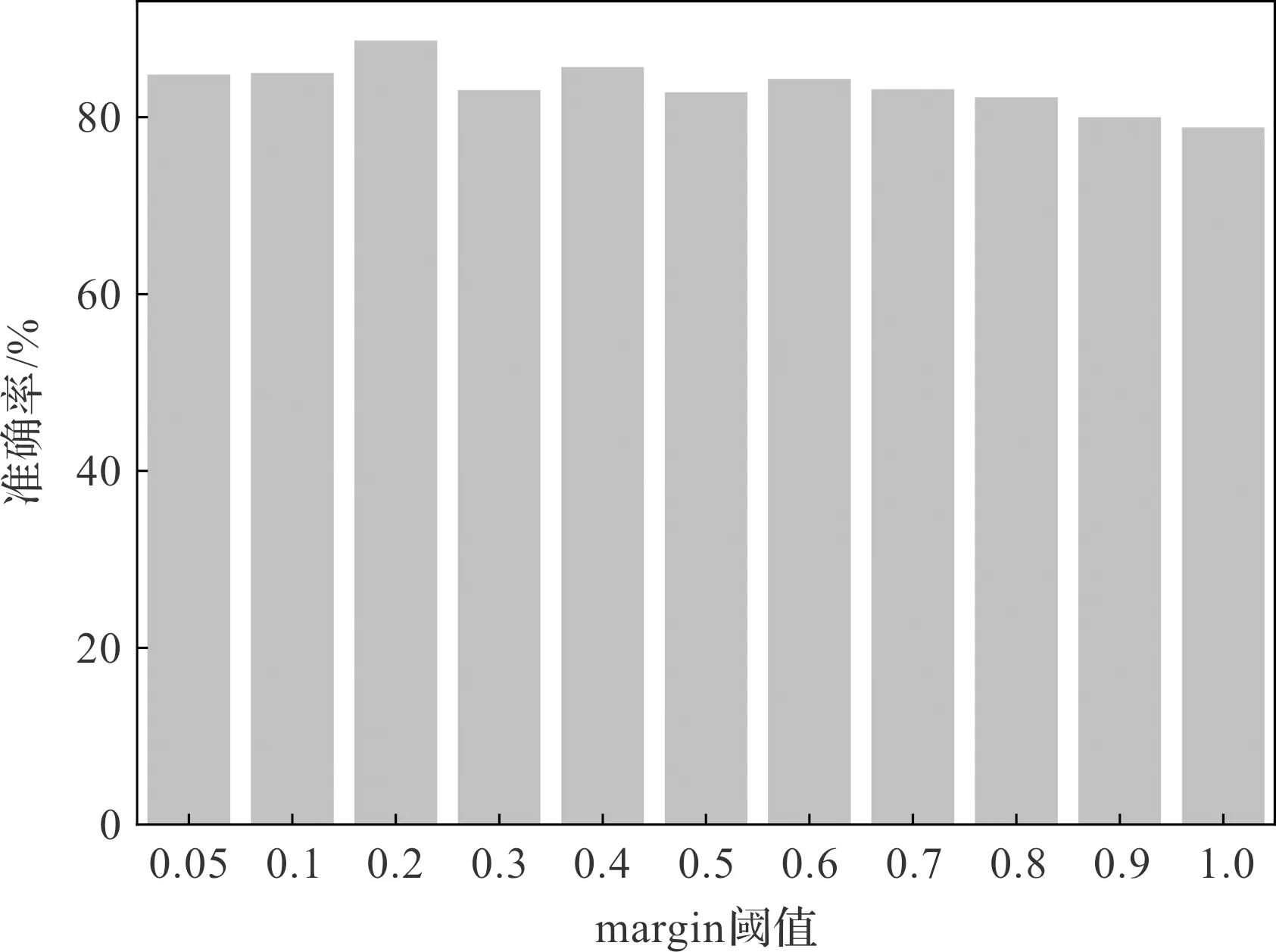
图7 margin值对故障诊断的影响

图7中,当margin为0.2时,故障诊断精度最高,所以后续实验的margin值均为0.2。

2.1.2 训练样本数量对诊断精度的影响

为探究笔者所提模型在小样本下的故障诊断精度,该实验从表2训练集各类故障中分别随机选取了5、10、15、30、50、80和100个作为模型训练集,对比训练样本数量对模型诊断精度的影响;同时,将其与1DCNN模型和2DCNN模型作对比。

其中,1DCNN模型是由4层一维卷积和全连接层组成的一维卷积神经网络,2DCNN与笔者所提模型的结构参数相同,不同之处是2DCNN模型在输出低维特征后直接连接全连接层对故障进行分类。各模型使用相同的训练参数,详细参数见2.1.1节。

各模型共迭代40次,重复实验5次,取其平均值,得到不同模型在轴承数据中的故障诊断实验结果,如图8所示。

图8 不同模型在轴承数据中的故障诊断结果

从图8中可知:

3种模型整体的诊断精度随着训练样本数量的增加而提高,2DCNN模型和笔者所提模型的诊断准确率明显高于1DCNN模型,笔者模型和2DCNN模型在每类故障样本量大于30时,两个模型的诊断精度较为接近,并且都大于80%;

在训练样本量较少时,笔者模型的诊断精度明显大于其他两个模型;在每类故障样本量为15时,笔者模型的故障识别率比2DCNN模型高14.33%,比1DCNN模型高33.83%;即使是在每类故障样本只有5个时,笔者模型的故障识别率也有68%,比2DCNN模型高15.33%,比1DCNN模型高33.5%。

2.2 齿轮数据

美国康涅狄格大学齿轮数据集[17]共有9种故障状态:健康、缺齿、根裂、剥落和5种不同程度的齿削尖。故障信号的采样频率为20 kHz。

此处的实验选取了健康、缺齿、根裂、剥落和1种齿削尖共5类故障样本作为训练集和测试集,故障信号的预处理和数据划分方式与江南大学轴承数据集相同。

数据集划分结果如表3所示。

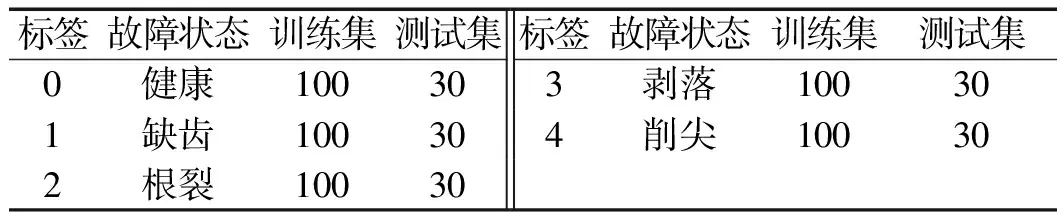
表3 齿轮数据集划分结果

从训练集的各类故障中,笔者随机选择5、10、15、30、50、80和100个样本,对比模型在不同训练集数量下的故障识别率,并将其与1DCNN模型和2DCNN模型对比。

1DCNN模型和2DCNN模型结构、实验的训练参数与江南大学轴承数据集实验相同,重复实验5次,并取平均值,得到的实验结果如表4所示。

表4 不同模型在齿轮数据中的故障诊断结果

由表4可知:模型故障诊断识别率与训练样本数量呈正相关,2DCNN模型和笔者模型明显优于1DCNN模型;在每类故障样本为10训练的3个模型中,笔者模型故障识别率高出2DCNN模型14%,高出1DCNN模型28.13%;甚至在每类故障样本只有5个的情况下,笔者模型的故障识别率依旧可以达到96.8%,高出2DCNN模型26%。

综合笔者模型在江南大学轴承数据集和康涅狄格大学齿轮数据集上的表现,笔者模型在训练集样本较为充足的情况下,故障诊断精度与其他模型相差无几;但是在训练样本不足时,笔者模型的故障识别率明显优于其他模型,并且仍具有较高的故障识别率。

3 特征可视化

深度神经网络的可解释性仍然是当前的研究热点和难点,其工作原理让人难以理解。但是,其可视化部分模型的特征层可以加深对模型的理解。笔者选用在康涅狄格大学齿轮数据集中,每类故障样本为10训练好的2DCNN模型和笔者模型,把测试集样本输入模型,使用T-SNE(T-distributed stochastic neighbor embedding)[18]可视化两个模型在平均池化层后输出的低维特征,其中,T-SNE可以将高维数据映射到低维空间。

笔者将模型输出的低维特征映射到二维空间,并将其可视化,如图9所示。

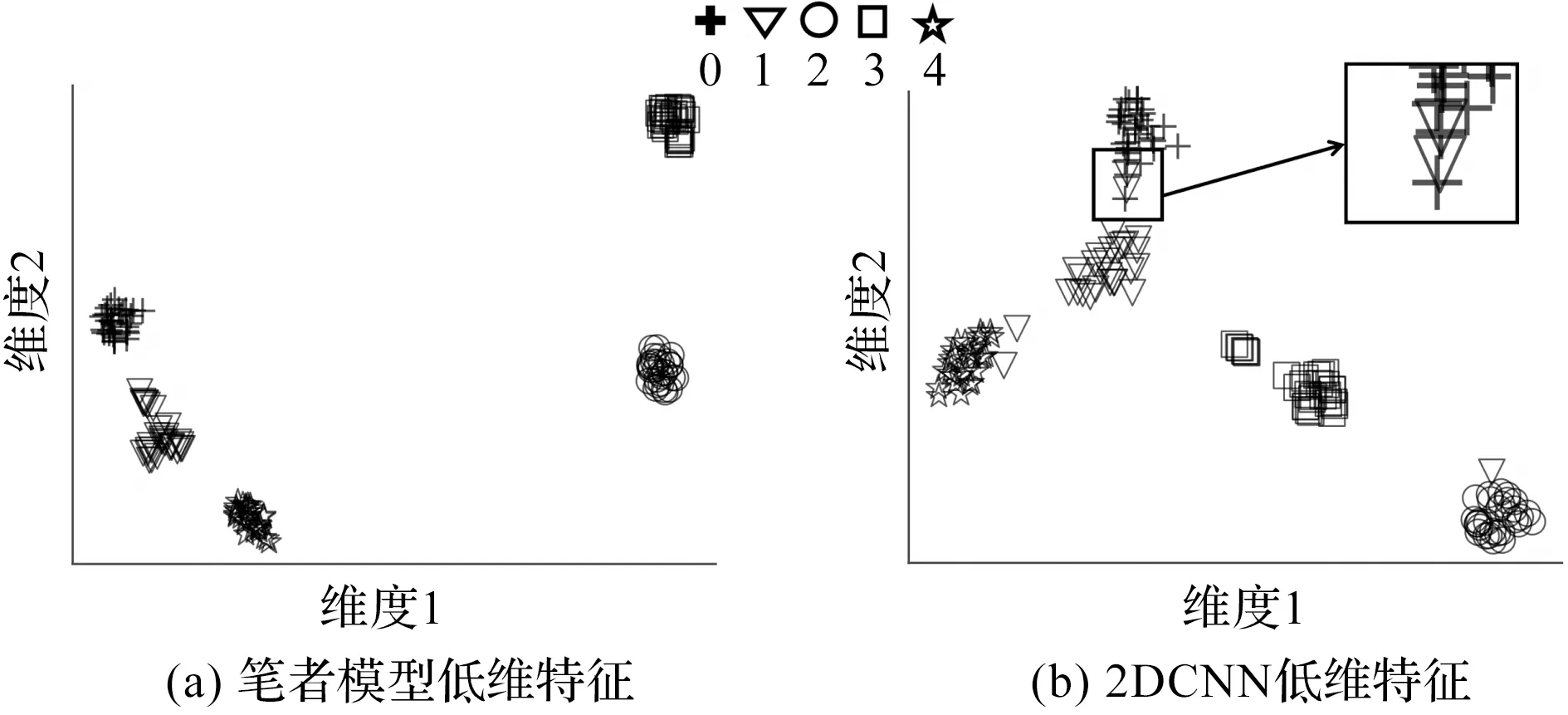
图9 不同模型低维特征可视化对比结果

0、1、2、3、4和5分别与表3中的标签相对应,表示不同的齿轮故障。

从图9中可以观察到:2DCNN模型中的故障1与其他故障交织在一起,与不同故障的分界不明显,容易产生错误的故障分类结果;相对于2DCNN模型,笔者模型中相同故障样本的分布更加紧凑,不同故障样本的分布区别明显。

为了解2DCNN模型和笔者模型在齿轮数据中的分类情况,笔者绘制了混淆矩阵，如图10所示。

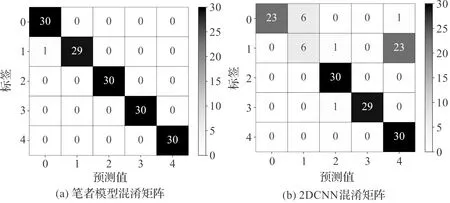
图10 不同模型混淆矩阵对比结果

混淆矩阵的标签轴为真实的故障标签,预测值为模型的预测的故障类别。

从图10中可知:笔者模型在各类故障上的识别率高于2DCNN模型,2DCNN模型对于故障1的识别误差较大。

4 结束语

笔者提出了一种在小样本数据集下机械设备典型部件的故障诊断方法,该方法可分为故障特征提取和故障诊断两个阶段。首先采用度量故障样本特征相似度的方法,来优化模型提取的特征;再通过比较未知样本与已知样本特征的相似度,实现对未知样本的故障识别。

研究结论如下:

(1)采用短时傅里叶变换,将原始时序信号转换为时频域信号,充分挖掘原始数据信息;同时,将一维信号转换为二维图像,充分利用卷积神经网络在图像特征提取上的优势,使模型的特征提取能力得到显著提升;

(2)利用基于Triplet Network搭建的模型提取故障样本时频信号低维特征,通过度量锚点与正样本低维特征和锚点,以及负样本低维特征的相似度,优化模型的特征提取策略;

(3)通过轴承故障数据集和齿轮故障数据集验证笔者所提方法,结果表明,该方法在小样本数据下的故障诊断性能明显优于1DCNN和2DCNN;在每类齿轮故障样本只有5个的情况下,该方法的故障识别率依旧可以达到96.8%,比2DCNN高26%,比1DCNN高33.5%。

综上所述,笔者所提方法在小样本数据集下机械设备典型部件的故障诊断中具有较优的性能。

下一步,笔者考虑将该方法应用于变工况场景下旋转机械典型部件的故障诊断中,以提高该方法的泛化能力和鲁棒性。