受轴向激励弹性支承梁的稳定性分析

张弛 毛晓晔 丁虎 陈立群

（上海大学力学与工程科学学院，上海 200444）

引言

弹性支承梁是工程结构中最重要的元件之一，工程中的梁结构与相邻的系统相互作用，承受载荷，当受到激励作用时，结构的支座弹簧和阻尼可以有效缓解激励作用，提高结构抗力[1，2]，采用弹性支承梁可以提高结构稳定性，而且理论上弹性结构的约束也不可能是绝对的刚性支撑，所以弹性支承梁在建筑、桥梁和防护工程中都有广泛的应用，如防冲击梁结构[1]，以及弹性橡胶支座的桥梁结构[3].同时，飞机中的管道结构也可简化为梁模型，这类管道在非定常流或外界激励影响下会发生剧烈振荡，进而损坏[4]，这类问题引起了学者们的广泛关注[5，6].Mao等[7]研究了超临界条件下，输流管道3：1内共振的稳态响应.Tan等[8-10]采用Timoshenko梁模型对输流管道进行了一系列研究.较早的研究者多将目光集中于轴向运动速度和系统固有频率之间的关系，以及临界流速处的发散失稳上.这些研究往往都是基于理想化的支承情况，在实际工程中已有使用弹性支承构件减轻结构振动的实例.

1996年，Kang和Kim[11]研究了弹性支承梁和板的模态特性与横向自由振动.2000年，夏季和朱目成等人给出了带有多个弹性支承与集中质量的梁的固有频率的精确计算方法[12].之后Li使用了一种新的方法来分析两端具有任意弹性支承边界梁的模态特性[13]，并将其推广到二维问题的研究中[14，15].2013 年，Li等[16]在梁的两端同时加上了扭转弹性约束和竖向弹性支承约束并研究了其对梁固有频率的影响.2017年，Gan等[17]利用有限元建模，研究了中间弹性支承的位置和刚度对动点荷载作用下功能梯度欧拉-伯努利梁振动的影响.2018年，Ding等[18]研究了弹性支承弹性结构的力传递问题并证明了其研究的必要性，之后Ding等[19]分析发现弹性边界会对弹性梁非线性特性产生显著的影响.然而，以上工作大部分是对弹性支承结构的自由振动或是其在横向激励下受迫振动的研究.近年来关于轴向运动体参激振动的研究受到广泛关注[20-25]，2019年，Li等研究了两端带有弹簧支撑的轴向运动梁的特性，分析了弹簧刚度对临界速度的影响，同时通过力传递率研究了系统的隔振效果[26].而受轴向力激励的弹性支承梁的相关研究仍然较少.

对于工程中普遍存在的受轴向载荷梁，早在1975年，Shaker[27]就已经分析了轴向载荷对端部带有集中质量均匀悬臂梁固有频率和振型的影响.到上世纪90年代，已有许多相关的研究成果[28-32].2000年，Ji和Hansen[33]对一端固定一端滑动屈曲梁在轴向简谐载荷作用下的非线性响应进行了实验研究，同时还考察了不同阻尼下的不稳定区和混沌响应区.2004年，Naguleswaran[34]研究了均匀欧拉-伯努利梁在沿轴向线性分布全拉伸、部分拉伸和全压缩轴向力作用下的横向振动.2005年，Liu和Chang[35]研究了一般边界条件下磁弹性梁在磁力、轴向力和弹簧力作用下的振动.Pratiher和Dwivedy[36]采用多尺度法确定了端部质量悬臂梁在时变磁场和轴向力作用下的参数不稳定区，得到了各个系统参数对参数失稳区域的影响.2008年，Yang等[37]对含开口边裂纹非均匀欧拉-伯努利梁受轴向压力和沿纵向移动集中横向载荷的自由振动和受迫振动进行了分析研究.2011年，Li等[38]对具有初始轴向张力简支纳米梁的横向振动展开了研究，发现外部轴向张力和非局部纳米尺度参数对非局域纳米梁的非线性振动行为有重要影响.2015年，Li[39]提出了一种解析方法，并采用该方法和有限元法分别计算了两端铰支梁和两端固定梁在轴向拉力和轴向压力作用下的动力响应，验证了其有效性.2020年，Zhou等[40]研究了轴向基础激励与内流速度对输液管道非线性受迫振动的联合影响.同年，Zhao等[41]提出了轴向压缩载荷作用下耦合Timoshenko双梁系统横向受迫振动的适用于任何边界条件的广义解，并讨论了高长比、剪切效应、转动惯量等物理参数以及轴向压缩载荷的影响.不过，这些研究中梁都是建立在简支、固支、自由几种典型边界上.当边界受弹性约束，受到轴向力作用梁的临界屈曲轴力、振动稳定性都可能会发生变化，这对于弹性结构稳定性设计至关重要.目前尚未有相关研究成果发表.

基于以上调研，本文将重点研究支撑弹簧刚度对受轴向激励弹性支承梁横向非线性振动的影响.第一节利用Hamilton原理建立受轴向激励弹性支承梁的非线性动力学控制方程.第二节进行模态分析，研究支撑弹簧刚度对系统临界轴力和固有频率的影响.第三节将使用Galerkin法将方程进行截断，得到一系列常微分方程，并进行无量纲化.第四节利用多尺度法对该参激振动进行近似解析求解，分析激励幅值、支撑刚度、平均轴力等参数对系统非线性响应的影响，然后通过稳定性分析研究支撑弹簧刚度、阻尼系数对系统稳定边界的影响，并进行数值验证.第五节得到结论.

1 数学模型和控制方程

如图1所示，梁的长度为L，两端弹簧支承刚度分别为KL和KR，ρ为梁的质量密度，A为横截面面积，E为弹性模量，I是梁关于中心轴的横截面惯性矩.梁受轴向张力P，该轴向力由平均张力P0与脉动张力P1组成.

图1 受轴向激励弹性支撑梁物理模型Fig.1 The model of axially excited beam with elastic boundaries

利用Hamilton原理建立系统运动控制方程

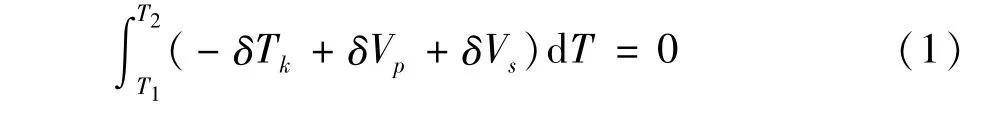
其中，δTk为梁的虚动能，δVp为梁的虚势能，δVs为梁两端支承弹簧的虚势能.梁的虚动能的表达式为

其中W（X，T）和 U（X，T）分别表示梁的横向位移和纵向位移，由于纵向位移微弱，可以忽略不计.梁的虚势能的表达式为

其中 ε（X，Z，T）和 σ（X，Z，T）分别是非线性轴向Lagrange应变和轴向扰动正应力.采用Kelvin黏弹性本构关系模型

2 模态及频率

严格满足非线性偏微分方程的解是几乎不可能得到的，按照动力学经典方法，首先基于线性派生系统，求得满足边界的模态函数，因此忽略控制方程中的非线性项、阻尼项，得到系统的线性派生方程及其边界条件

其中C1为非零常数.如果存在非平凡解，那么系数矩阵行列式值为零，由此求得系统的固有频率.

表1给出了本文研究的梁的物理参数值以及几何参数值.

表1 梁的材料参数Table 1 Material parameters of the beam

图2给出了在不同支撑弹簧刚度下，系统第一阶固有频率随轴向张力的变化情况.可以看出，随着轴向张力的增加，梁的固有频率逐渐减小.当梁的第一阶固有频率为零时，结构发生静态失稳（又称屈曲失稳），此时对应的轴向力称为临界轴力.由图2中可知对应的临界轴力如表2所示：

图2 不同支撑刚度下的第一阶固有频率Fig.2 The first natural frequencies of different supporting stiffnesses

表2 不同支撑刚度对应的临界轴力Table 2 The critical axial force of different stiffnesses

表2的结果表明，对称支撑条件下，弹簧刚度的大小对临界轴力没有影响.

3 Galerkin截断

4 参激共振稳态响应

4.1 多尺度法分析过程

用于数值计算的梁参数与表1相同，系统的初始轴力为200 N，激励幅值为60 N.Runge-Kutta法数值计算时长取1000个周期，每个周期内取50个点，初始位移均取为4×10-4，初始速度均取为0.

图3（a）和图 3（b）分别为 kL=kR=50，ωb=2ω1=58.07Hz时的全局和局部时程图，可以看出此时系统已经进入稳态响应，仿真时长足够，取响应进入稳态最后一个周期响应的最大位移作为幅值，验证弹性梁稳态响应的近似解析解.

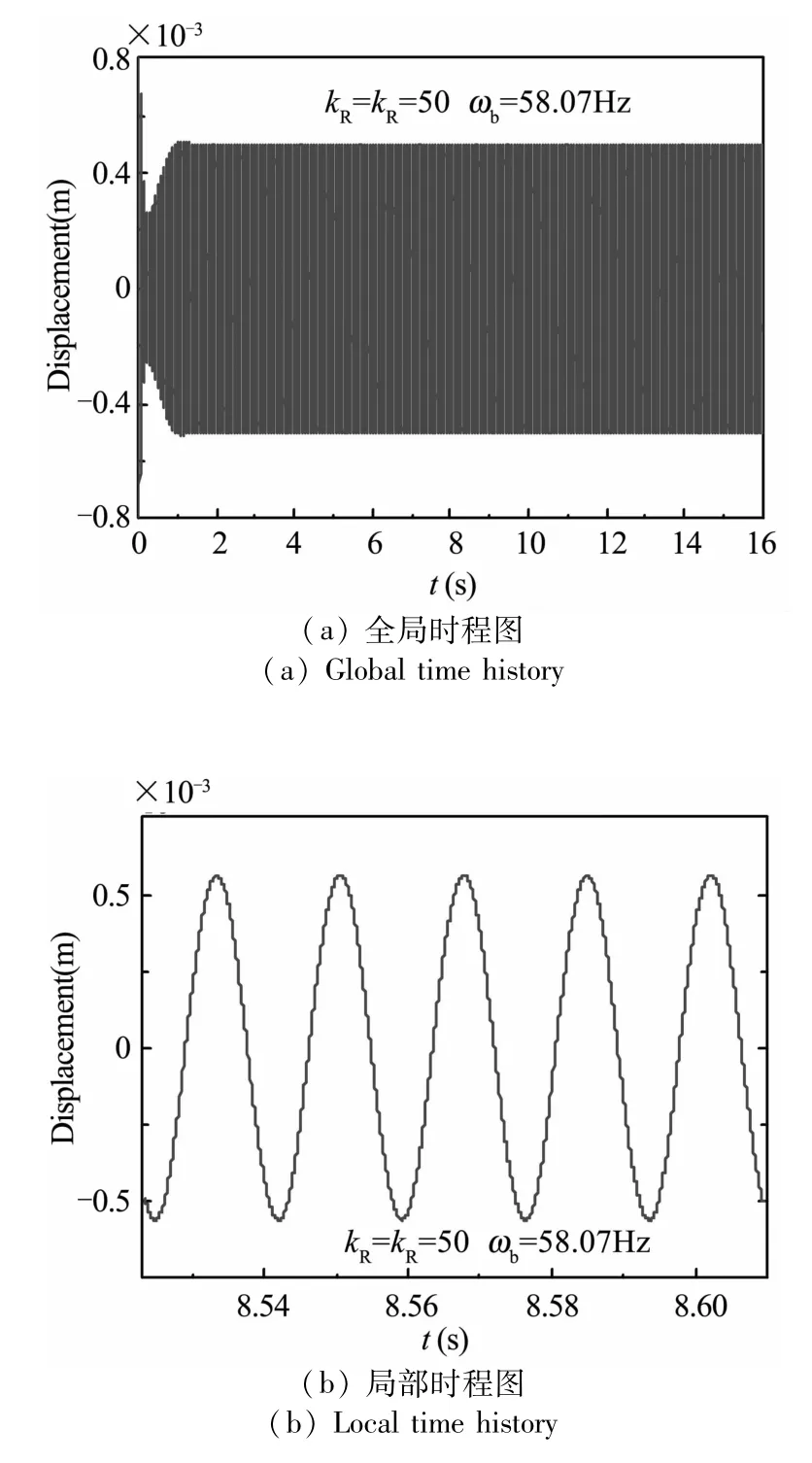
图3 梁中点处稳态响应时程图Fig.3 Time history of steady-state response

图4（a）和图（b）对比了两组刚度下通过二阶、四阶、六阶截断得到梁中点处稳态响应的数值仿真结果.观察发现，二阶截断在共振区域边缘处，振幅较小时与四阶和六阶截断得到的结果差异较大，而四阶和六阶截断的结果吻合得很好，故本文后续研究均采用四阶截断，取n=4.

图4 不同截断阶数对比Fig.4 Comparison of different truncation orders

图5利用Runge-Kutta法计算的数值解对多尺度近似解析结果进行了验证，图中实线代表近似解析解，散点代表数值仿真实验结果.从图中的对比可以发现，近似解析解具有令人满意的计算精度，因此，本文接下来采用近似解析法对系统的动力学响应做进一步分析.此外，由于立方非线性产生作用，且立方非线性项系数为正数，所以稳态响应共振峰向右偏移，系统呈现硬非线性特征.

图5 梁中点处幅频响应解析与数值结果对比Fig.5 Comparison of analytical and numerical results

4.2 稳定性判断

为了研究零解的稳定性，按照am和βm提取方程（43）左端的Jacobian矩阵，得到：

根据Routh-Hurwitz判据，可以得出二次代数特征方程根不包含正实部的充分必要条件是特征方程中所有的系数均为正数，可得：

图6给出了支撑刚度KL=KR=5741.67N/m（kL=kR=50）时，阻尼系数对系统稳定区域的影响.从图中可以看出，系统的稳定性随着阻尼的增大而增大，且越靠近共振区域影响越显著.这表明提高系统的阻尼，不仅可以提高发生参激共振的阈值，而且在同样的脉动压力下，系统必然发生参激共振的带宽也会缩小.图7给出了阻尼系数α=1.389 ×10-7N s/m2（μ=2）时，支撑弹簧刚度对系统稳定区域的影响.从图中可以看出，系统的稳定性随着刚度的增大而减小，且越远离共振区影响越显著.这种趋势表明，适当降低两端约束的刚度对抑制参激共振是有利的，不仅可以提高参激共振的阈值，还能在同样的激励条件下，显著减小系统必然产生参激响应的带宽.

图6 阻尼系数对系统稳定性的影响Fig.6 The influence of damping coefficient

图7 支撑弹簧刚度对系统稳定性的影响Fig.7 The influence of supporting spring stiffness

图8（a-c）分别给出了在不同支撑刚度、不同激励幅值以及不同平均轴力下系统共振区域附近的非线性响应，图8（d）则展现了在平均轴力和支撑刚度共同作用下系统的非线性响应，其中虚线代表不稳定解，实线、点线与点划线代表稳定解.从图8（a）中可以看出，系统呈现出硬非线性特征，而随着支撑刚度的增大，系统的固有频率增大，共振区域向高频移动，发生共振的区间增大，同时系统的硬非线性特征增强.由图8（b）可以看出，随着激励幅值的增大，两支解的间距增大，系统发生共振的频率区间变大，在相同激励频率下，共振幅值也同时增大，系统的软硬特性不变.由图8（c）可见，当平均轴力增大时，共振区域向低频移动，发生共振的区间和共振幅值增大.从图8（d）中可以看出，当支撑刚度和平均轴力都较大时，系统的失稳区域较大，此时最易发生参激共振进而导致失稳.

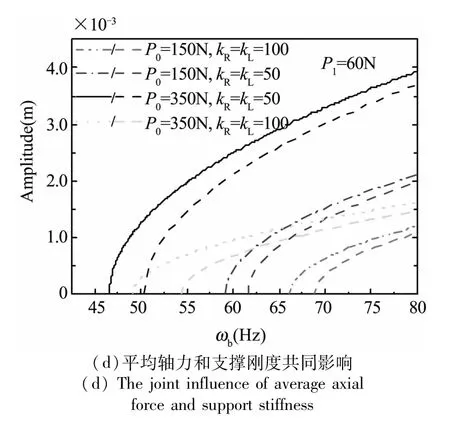
图8 系统参数对非线性响应的影响Fig.8 The influence of system parameters on nonlinear response

可以看出当两支解的间距越大，系统必然发生参激共振的区域越大，支撑刚度越小系统的稳定区域越大，这与上一小节中得到的结果相符，但还发现：减小支承刚度增大稳定区域的同时系统的共振幅值也会有所增大，这说明系统一旦发生参激共振，振动将会更加剧烈，在实际工程中需要更加注意.而当外激励频率不变时，也可以通过改变支承刚度来避开共振区域以达到保护结构的目的.对于激励幅值和平均轴力，系统稳定区域随其增大而减小，共振幅值随其增大而增大.

5 结论

本文以受轴向激励弹性支承梁为研究对象，采用Hamilton原理进行了动力学建模，并进行了模态分析，求得了系统固有频率.然后利用Galerkin截断方法分别与多尺度法和Runge-Kutta方法结合，求得了近似解析解与数值解，并基于这两种结果分析了激励幅值、弹簧支撑刚度和平均轴向张力对系统非线性响应的影响.之后根据求得的近似解析解，通过Routh-Hurwitz稳定性判据，得到了系统在不同阻尼系数和支撑弹簧刚度下的稳定边界，并进行了数值验证.经过研究发现，系统的固有频率会随轴向压力的增大而减小，随着支撑弹簧刚度的增大而增大，但是使系统发生失稳的临界轴力并不会随对称的支撑弹簧刚度发生变化；增大阻尼系数可以增大系统的稳定区域，并且越靠近共振频率，阻尼系数的改变所产生的影响越大；减小支撑弹簧刚度将增大系统的零解稳定区域，且越偏离共振频率，弹簧刚度的改变所产生的影响越大；整个非线性系统呈现硬特性，随着支撑刚度的增加或平均轴力的减小，系统的硬特性增强.而随着支撑刚度的减小、平均轴力的增大或激励幅值的增大，系统的共振幅值增大.总之，以上研究结果将为工程中大量存在的弹性体稳定性设计提供理论指导.