环形天线结构的复杂动力学研究*

马文赛 吕书锋† 杨绍武 张伟

（1.内蒙古工业大学理学院，呼和浩特 010051）（2.北京信息科技大学机电学院，北京 100192）

（3.北京工业大学材料与制造学部，北京 100124）

引言

航天技术的迅速发展对新型卫星天线技术提出了更高要求，大口径、高精度、低质量以及高强度等特征已成为大型卫星天线设计的必然趋势.环形桁架可展开结构具有应用空间大、结构形式简明的特点，天线口径可达50米，但质量并没有随口径的增大成正比例增加，也不会改变结构形式，因此环形桁架可展开结构是目前大型卫星天线较为理想的结构形式.目前，地球观测，陆地遥感以及声控探测等都受益于环型桁架卫星.然而目前国内对环形桁架可展结构的理论和实践都十分匮乏，因此对环形桁架可展结构在太空条件下振动的理论研究是十分迫切和重要的，它能够为将来实践提供理论基础.本论文的桁架采用复合材料，通过均匀化理论将环型桁架等效成圆柱壳结构，得到环型桁架的等效刚度，从而将环型桁架等效成圆柱壳.

可展开结构工作过程如下：在航天器发射前处于收拢状态，在发射入轨接受到指令后开始展开，完成展开后锁定并且保持工作状态.陈务军等[1]介绍了大型构架式展开天线关键部件的设计构思，主要包括：天线总体选型及布置，单向折叠展开臂支撑背架，复合剪式铰外环，馈源支架，索网设计与反射面调整，180°能量铰等驱动机构.Li[2]对环形桁架可展开天线的展开动力学进行了仿真，总结了初始速度、阻尼和重力对展开的影响.在考虑扭转弹簧刚度、节点阻尼、重力和网架预张力的情况下，对环桁架可展开天线展开动力学进行了分析和控制.Morterolle等[3]提出了一种计算测地张力桁架的新方法，既保证了节点的正确定位，又保证了张力的均匀性.You等[4]提出了一种考虑系统铰链间隙和反射面柔性影响的卫星天线系统建模与分析方法.Zhang等[5]对高波束指向精度网状天线进行了一种两步结构设计.此外，胡海岩等[6]综述了大型可展天线研究现状和进展，提出了大型可展天线在结构设计、动力学建模与控制和仿真模拟实验中需要注意的问题.

圆柱壳结构的动力学分析对工程设计具有非常重要的指导意义.在一些实际工程应用中，非线性振动系统会出现在线性系统中不出现的现象，如跳跃、分叉以及混沌运动等.由于不同振动模态之间可能会产生相互作用，从而导致系统振动模态之间出现能量交换，进而产生复杂的非线性动力学问题，因此研究环形桁架等效圆柱壳的非线性内部共振及其复杂动力学特性对工程实际问题具有重要的理论指导意义.Liu等[7]研究了复合材料层合圆柱壳的非线性振动问题.Zhang等[8]研究了空间环境中圆形网格天线在热激励下的连续模型和非线性动力响应.Yang等[9]研究了碳纤维增强聚合物（CFRP）层合圆柱壳在1：2内共振、主参数共振和1/2次谐波共振下的非线性振动.Wu等[10]研究了圆形桁架天线在展开锁定情况下的频率特性.综上文献可以看出，研究环形天线结构等效圆柱壳的全局分叉和多脉冲混沌动力学的文献较少.然而，全局分叉和多脉冲混沌动力学的研究有助于解释环形天线结构等效圆柱壳多脉冲跳跃现象以及混沌现象，从而发现系统不稳定的机理，便于对系统进行有效控制.

在实际工程问题中，高维扰动非线性Hamilton系统可以用来描述实际工程所抽象出来的数学模型和动力学方程，并且高维非线性系统的全局分叉和混沌动力学能够揭示系统的运动不稳定性和复杂的动力学行为.对于高维系统，许多学者把Melnikov方法和其它摄动方法结合，改进和发展了Melnikov方法，使该方法成为了研究混沌运动的解析方法.Camassa等[11]发展了研究一类四维具有作用-角变量的非线性系统在耗散扰动下系统多脉冲混沌动力学的广义Melnikov方法，该方法可以研究各种类型的多脉冲同宿轨道存在的条件.Kovacic和Wettergren[12]利用Melnikov方法和几何奇异摄动方法研究了共振受迫耦合双摆的全局动力学.Zhang和Chen[13]应用广义Melnikov方法分析了1：2内共振下复合材料层合板的全局分叉和混沌动力学.Wang[14]应用广义Melnikov方法讨论了受迫双层纳米板的同宿现象和多脉冲混沌运动.Zhang等[15]研究了参数激励与外激励联合作用下偏心旋转环桁架天线的多脉冲跳跃双参数混沌动力学.秦琅等人[16]考虑了一个含小阻尼、受周期激励的单自由度干摩擦振子，运用Melnikov方法得到了系统出现马蹄型混沌的参数区域.李海涛等[17]对带有非对称势能阱的双稳态能量采集系统开展混沌动力学研究，通过Melnikov方法获得发生同宿分叉的阈值，并使用数值方法验证了理论结果的有效性.Ngouabo等[18]利用Melnikov定理研究了静电微电子机械系统的非线性分析问题.此外，李双宝等[19]将Melnikov方法推广到非光滑系统中，且对该方法的应用进行了全面综述和比较.

本文基于坐标变换理论和恰当横截面，发展了高维Melnikov理论，使其适用于研究五维含参非线性动力系统，并应用于研究横向激励和面内激励联合作用下环形天线结构的复杂动力学.将环形天线结构的力学模型简化为五维自治非线性动力系统，通过定义恰当横截面，将高维Melnikov函数引入四维摄动相空间，证明环形天线系统中存在Smale马蹄意义下的混沌运动.以激励系数和阻尼系数作为控制参数，研究系统参数对环形天线系统稳定性和混沌运动的影响.利用相图、庞加莱图，数值模拟给出系统的混沌运动区域，验证理论结果的正确性.

1 五维非线性系统的Melnikov方法

文献[11]给出了四维自治Hamilton系统的广义Melnikov方法，且应用于研究了共振受迫弱非线性耦合摆系统的复杂动力学[12].然而，工程系统中的大多问题的数学模型可用高维非自治非线性系统来描述.本文通过引入恰当横截面，部分改进了广义Melnikov方法，使其适用于研究直角坐标表示的高维非自治非线性系统.

我们在文献[11]的控制系统上，考虑如下耗散扰动系统：

是辛矩阵，H（u，v1） 是 Hamilton 函数，gu，gv1，gv2是关于t的周期为2π的扰动函数且光滑.

当方程（1）中ε=0时，其未扰动系统为

假设1 存在区间[L，N]中每一个变量v1，方程（3a）有双曲不动点 u=u0（v1） ，并且存在连接不动点 u=u0（v1） 的同宿流形 u=uh（t，v1），t∈ R.

如图1所示，流形M是具有三维稳定流形ws（M）和不稳定流形wu（M）的局部不变流形.方程（3）同宿轨道的存在性表明，稳定流形ws（M）和不稳定流形wu（M）相交于三维同宿流形Γ

图1 四维相空间未扰动系统几何结构Fig.1 The geometric structure of unperturbed system in four-dimensional phase space

由文献[21]可知，法向双曲不变流形M（ϕ）在小扰动维持局部法向双曲不变流形，可表示为

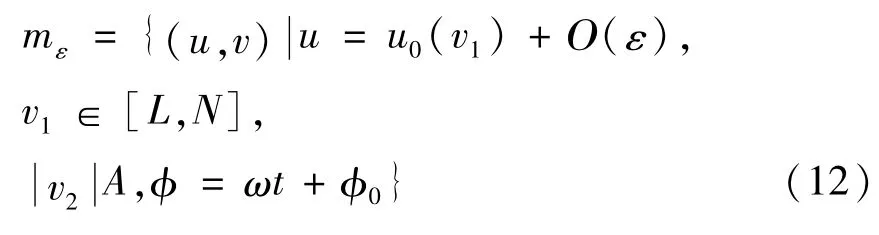
即扰动系统的法向双曲不变流形mε（ϕ）是ε阶逼近于未扰动系统的法向双曲不变流形M（ϕ）.

在五维相空间中定义横截面

图2为截面∑示意图.这里先取截面ϕ=ϕ0，这样就可以在四维空间研究系统（14）的非线性动力学特性，然后ϕ从0到2π变化，从而跑遍整个环面S1，进而研究系统（1）的非线性动力学特性.

图2 横截面Σϕ0的几何结构Fig.2 The geometric structure of the cross section Σϕ0

2 环形天线结构等效圆柱壳动力学方程

考虑圆柱壳中面半径为R，轴向长度为L，沿径向壳的厚度为h.假定圆柱壳的铺设层数为Ns，铺设顺序为（45-45）s.曲线坐标位于壳体的中面，圆柱壳内任一点的位移u，v，w分别沿x，θ，z方向.同时环形天线结构等效圆柱壳处于一个均布的热环境中，此环形天线结构等效圆柱壳受到边界上的一个径向线载荷f=F cos（Ω1t）和一个轴向载荷p=p0+p1cos（Ω2t）的共同作用，p0为面内预紧力，如图3所示.无量纲后的两自由度环形天线结构等效圆柱壳系统控制运动方程为[9]

图3 环形天线结构等效圆柱壳模型Fig.3 Equivalent cylindrical shell model of a ring antenna structure

为了方便应用广义Melnikov方法研究两自由度环形天线结构等效圆柱壳复杂动力学，这里主要研究主参数共振，引入以下坐标变换将阻尼系数 μ1和 μ2，激励幅值 p1、p2、F1和 F2，以及参数m6、m8、n5和n7视为开折系数，在开折系数前面加上小扰动ε，并引入以下坐标变换

3 系统的混沌运动分析及数值模拟

由方程（4）和方程（21b）可以定义环形天线结构等效圆柱壳系统的部分法向双曲不变流形

因此，我们可以选取适当的参数使得等式（28）和等式（29）成立，从而使得k-脉冲Melnikov函数存在简单零点.

现在求解可能存在的脉冲数k，有条件（21a），可令m5=1；由条件（21b）和条件（24）可求得∈（-1，1），且m2和ω1有如图4的关系.

图4 m2和ω1的取值关系Fig.4 The relationship between m2 and ω1 is given

且

图5为相位漂移角与二阶模态阻尼系数之间的关系，从图中可以看出，当阻尼系数变大时，相位漂移角逐渐变小，即随着阻尼系数的增大，环形天线结构等效圆柱壳系统可能由多脉冲跳跃变为单脉冲跳跃，最后不发生跳跃.

图5 Δv2和μ2的取值关系Fig.5 The relationship between Δv2 and μ2 is given

因此，适当地选取 μ1、μ2、m3和 m7可以使得 k≥1且k∈z+.根据定理1，系统（18）的稳定流形ws（M）和不稳定流形wu（M）横截相交，说明环形天线结构等效圆柱壳系统存在横截同宿轨道，既存在k-脉冲的混沌运动.

应用四阶Runge-Kutta算法和Matlab软件对系统（18）进行数值模拟，验证环形天线结构等效圆柱壳存在混沌运动等复杂的非线性动力学行为.根据前面的理论分析，分别取如下参数

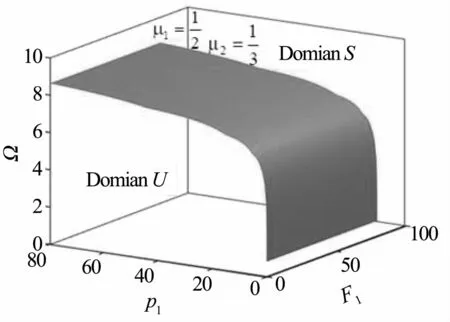
图6 阈值曲面及其两个参数空间Fig.6 Threshold surface and its two parameter spaces

图6表明，当阻尼系数μ1和μ2，以及激励频率Ω给定，激励幅值F1和p1位于阈值曲面的下方时，满足高维非自治非线性动力系统的横截相交条件，即环形天线结构等效圆柱壳可能发生混沌运动.

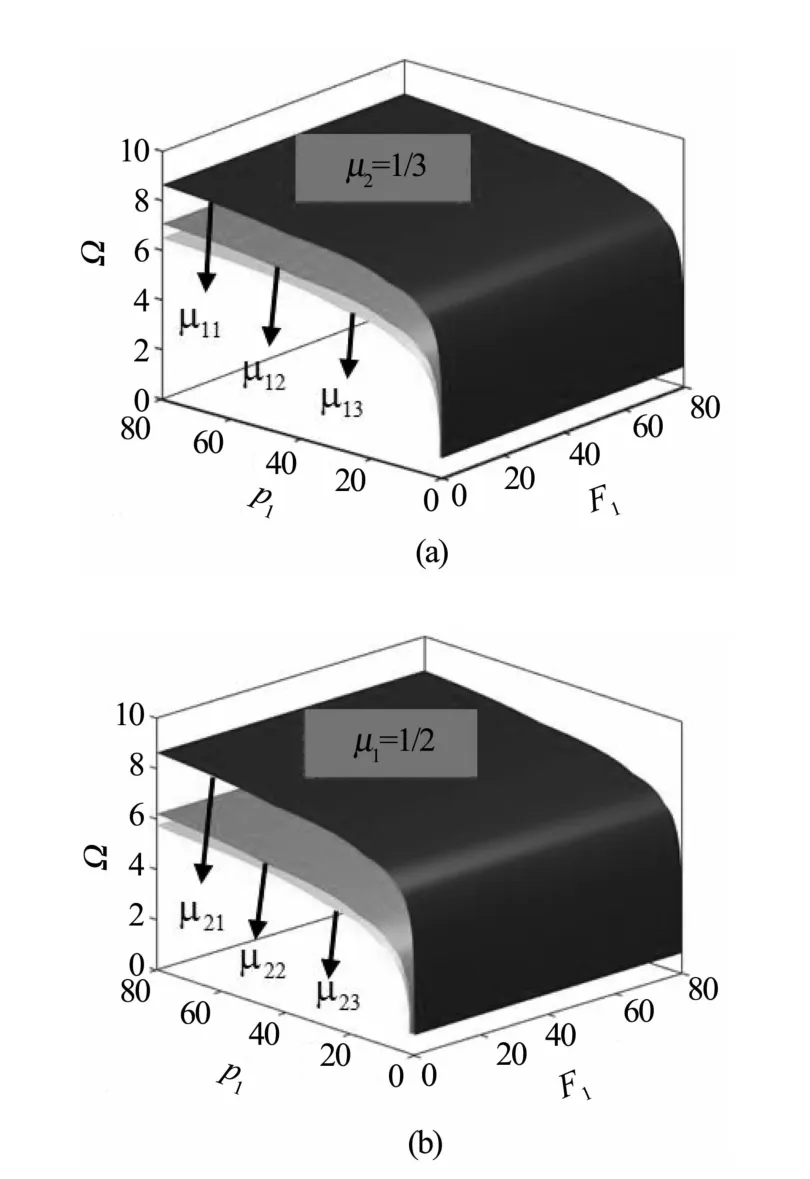
图7 不同阻尼参数μi（i=1，2）下的阈值曲面Fig.7 The chaotic threshold surfaces are obtained with different damping parameters μi（i=1， 2）

相图、庞加莱截面可以描述系统几何结构在相空间中的变化情况，这些不同的指标可以看作是混沌运动出现的证据.接下来将从这两个方面对环形天线结构等效圆柱壳的动力学进行分析.

图8和图9表示环形天线结构等效圆柱壳系统在平面 （x1，x2） 上的相图和平面 （x1，x2） 上的庞加莱截面图.

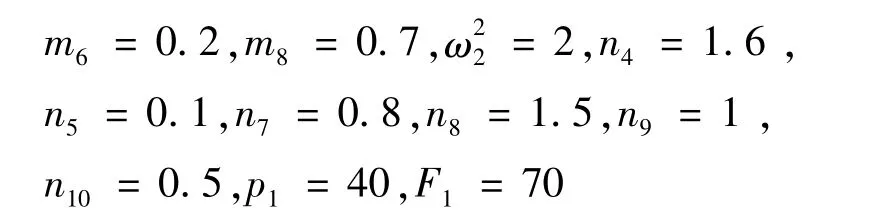
由图8可知，系统发生了混沌运动，且系统存在三个混沌吸引子，经计算，此时k=4.

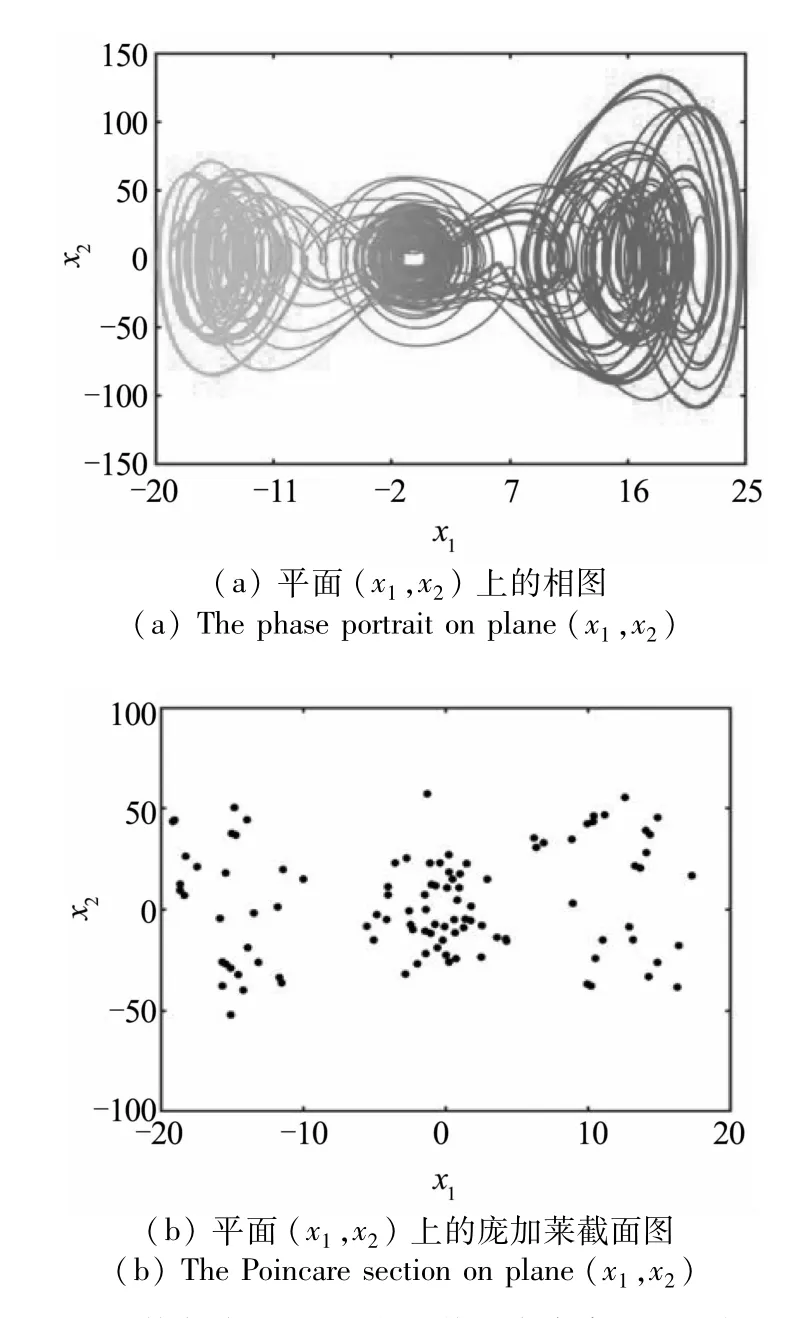
图8 外激励F1=70时，系统的多脉冲混沌运动图Fig.8 Multi pulse chaotic motion diagrams of the system when external excitation F1=70

图9为外激励幅值F1=100时，系统在平面（x1，x2）上的相图和庞加莱截面图.从图9可以看出系统一阶模态的振动幅度随着外激励的增大而增大.同样，由相图可以看出振幅在三个区域跳跃，天线整体等效圆柱壳结构在做呼吸形式的振动，且在正平衡点处的振幅大于负平衡点处的振幅，说明呼吸振动时天线结构的膨胀幅度大于收缩幅度.

图9 外激励F1=10时，系统的多脉冲混沌运动图Fig.9 Multi-pulse chaotic motion diagrams of the system when external excitation F1=10

4 结论

本章给出了改进的高维非线性系统广义Melnikov理论，并直接应用于环形天线结构等效圆柱壳高维非线性系统复杂动力学的分析，省略了通过奇异摄动法和规范型理论对系统方程化简的过程，使得理论分析结果更加接近原系统的性质.

应用广义Melnikov方法得到了参数激励和面内激励联合作用下环形天线结构等效圆柱壳发生混沌的条件.解析地研究了环形天线结构等效圆柱壳的全局分叉和Smale马蹄意义下的混沌运动，并且得到了环形天线结构等效圆柱壳可能发生混沌运动的参数域，为圆柱壳稳定性控制提供了有价值的参数指导.数值模拟进一步表明：

（1）环形天线结构等效圆柱壳发生混沌的参数域随着阻尼系数的增大而减小，说明环形天线结构等效圆柱壳在相对较小的阻尼下，更易发生Shilnikov型的脉冲混沌运动；

（2）从图8和图9的相图和庞加莱截面可以判断系统在正负以及原点三个平衡点处存在三个混沌吸引子，从而以这三个混沌吸引子为中心构成三个吸引域.从图8（b）和图9（b）轨线穿过庞加莱截面打点的位置可判断出随着外激励幅值的增大，一阶模态的正平衡点处吸引域增大，负平衡点处吸引域变小.