柔性关节柔性连杆机械臂的动力学建模*
张晓宇 刘晓峰† 蔡国平 刘传凯
(1.上海交通大学船舶海洋与建筑工程学院,上海 200240)(2.北京航天飞行控制中心,北京 100094)
引言
随着机器人技术的发展,近年来臂长更长的柔性机械臂在工业和航空航天领域引起了很大的关注[1,2].与传统的机械臂相比,此类机械臂通常具有更高的载荷/质量比和更低的能耗.然而,这些特点也导致机械臂产生变形以及较大幅度的振动,给高精度的控制带来了巨大挑战.一般而言,对于柔性机械臂这种复杂的机械系统,基于模型的控制方法比非基于模型的控制方法能获得更好的控制效果.即便如此,基于模型的控制方法也不能保证高精度的控制效果.为了获得更好的控制效果,除了选择合适的控制方法外,建立更合适的动力学模型也很关键.
到目前为止,国内外学者对柔性机械臂建模问题进行了大量研究.在早期的研究中,大多数研究人员认为,连杆的柔性是导致机械臂末端偏离目标位置以及系统发生振动的主要原因,并基于该想法提出了很多柔性臂建模方法.描述柔性杆的弹性变形时首先需要离散柔性体,常用的离散方法有假设模态法、有限元法和集中参数法等[3],其中,前两者是主流方法.假设模态法利用模态振型函数和模态坐标来离散系统的动力学方程,再利用模态截断缩小方程规模便于求解.先前已有研究人员使用这种方法对单连杆柔性机械臂进行建模[4,5],研究表明采用这种方法的实验结果与理论结果具有良好的一致性,然而这种方法及模型并不能很好地描述系统的细节特征[6].相对而言,有限元法没有这一缺点,一些文献研究了有限元方法在柔性机械臂建模中的效果[7-10],实验表明有限元方法也可以得到一个能较好地描述系统的模型.同时,研究人员发现在使用有限元方法时,采用一个单元就足以描述振动的前两阶模态,并能很好地反应柔性机械臂的动力学行为[8].随着研究的深入,研究人员注意到关节的柔性也是导致控制结果不及预期的关键因素之一.为了获得更好的控制效果,学者们开始对考虑关节柔性的机械臂动力学建模问题进行深入研究.例如,Xi和Fenton[11]在建立柔性机械臂动力学方程的过程中采用Spong模型[12]来描述柔性关节.如图1所示,经过简化后,柔性关节被两个刚性关节和一个扭簧所取代.作者在深入研究关节柔性对系统动力学特性的影响后,给出了系统振动频率和模态形状的参数化方法.文献[13-21]中,Spong模型也被用于建立同时考虑关节柔性和连杆柔性的机械臂动力学方程.这些研究的不同之处在于使用了不同的方法来离散柔性臂杆,如文献[13,17-19]中采用假设模态法来离散柔性臂杆,文献[14,16]中将柔性杆用连续梁模型计算,文献[15,20,21]中使用有限元法离散柔性臂杆.在获得动力学模型后,上述文献的作者们对柔性臂的模态分析、振动抑制以及柔性连杆与柔性关节耦合效应等问题进行了深入研究.研究结果证实,关节柔性确实会对系统动态特性产生比较大的影响,如果在柔性臂建模过程中忽略关节柔性,那将对系统动态特性分析和控制产生非常不利的影响.
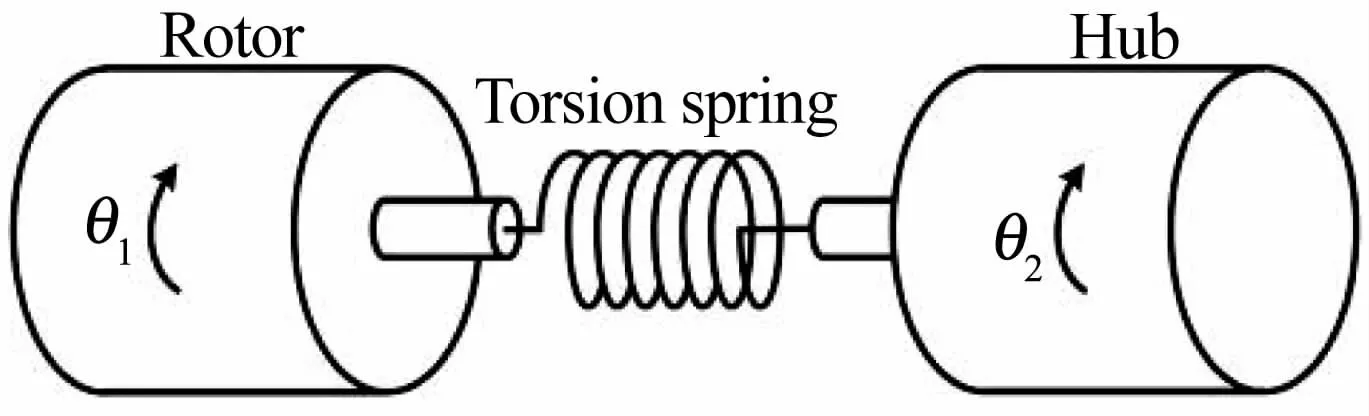
图1 柔性关节的模型Fig.1 Model of the flexible joint
从上述介绍可以看出,尽管目前关于柔性机械臂建模问题的研究已经取得了一些成果,但它们也存在一些不足.例如,被广泛采用的Spong模型,虽然可以比较简单地刻画柔性关节的动力学行为,便于建立柔性臂动力学方程,但也导致以下两个问题:一是关节柔性和连杆柔性之间的耦合效应不能被直接反映在动力学模型中,给系统动态分析带来不便;二是额外刚性关节的引入增加了系统的自由度,给机械臂控制器的设计带来不便.为了克服传统建模方法的不足之处,本文对柔性关节柔性杆机械臂的动力学建模问题进行了研究,并提出了一种改进的建模方法.在该方法中,柔性关节不再简化为两个刚性关节和一个扭簧,而是被简化为一个刚性关节和一个柔性连杆的弹性约束.这样处理的第一个好处是,关节柔性对连杆柔性的影响可以直接体现在梁的模态信息中;第二个好处是,系统无需引入额外的刚性关节,降低了系统的自由度和控制器设计的难度.在此基础上,本文根据哈密顿原理和假设模态法推导了柔性关节柔性杆机械臂的动力学方程.在文章最后,数值仿真结果验证了本文方法的有效性和优势.
本文的其余部分结构如下:第1节介绍了柔性关节模型的简化和柔性关节柔性连杆机械臂的动力学模型.第2节给出了单边弹性约束的柔性连杆的固有频率和模态函数的推导过程,并导出了离散形式的动力学方程.接着在第3节给出了数值仿真结果.最后在第4节给出了本文结论.
1 柔性关节柔性连杆机械臂的简化与动力学建模
如图2所示,柔性关节柔性连杆机械臂是具有强非线性和耦合特性的复杂机械系统.为了分析其动力学特性并设计运动控制器,需要建立系统的动力学模型.
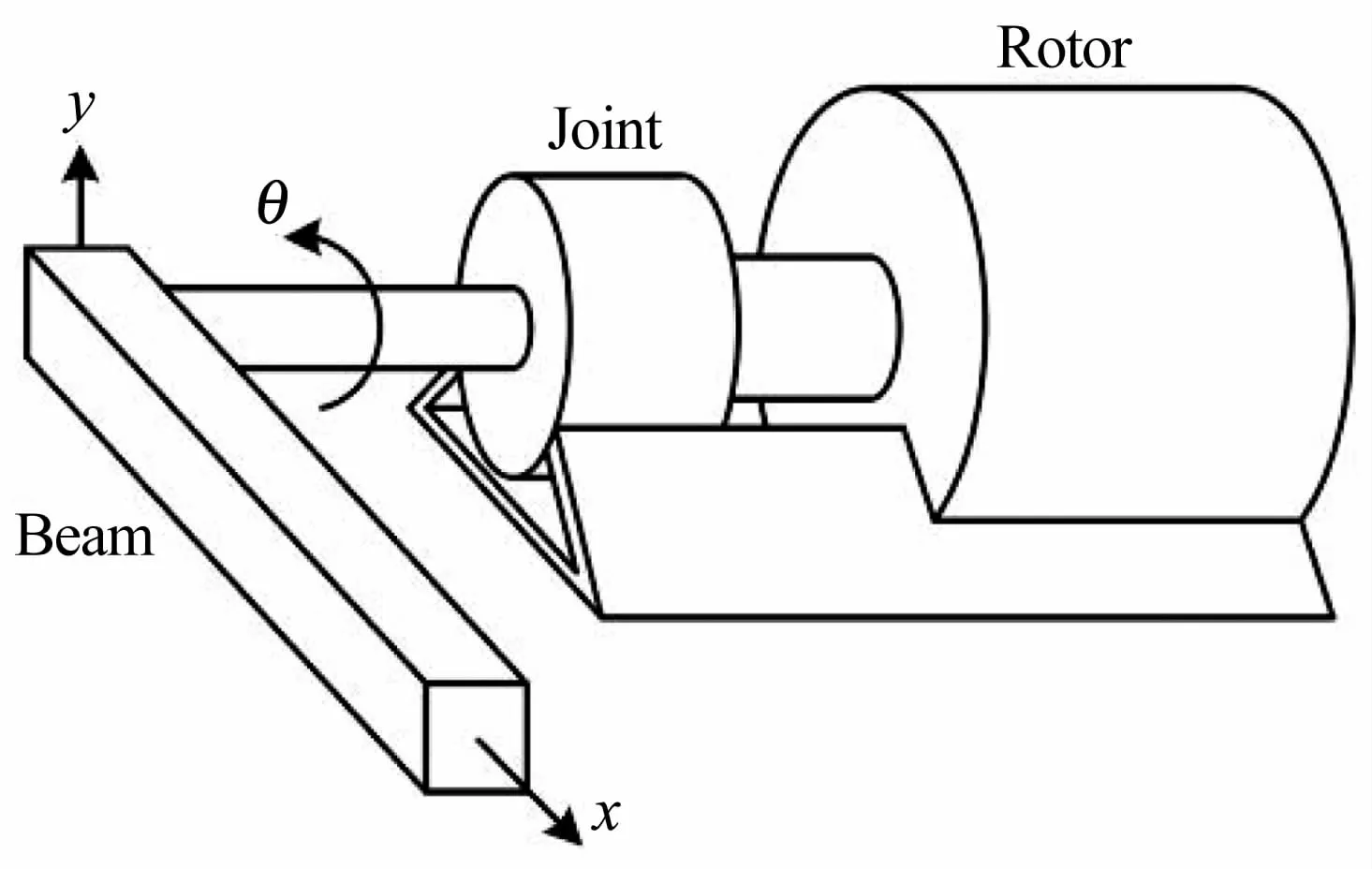
图2 柔性关节柔性连杆机械臂的模型Fig.2 Model of the flexible-joint flexible-link manipulator
合理简化物理模型是动力学建模的基础,其重要性不言而喻.从上一章节总结的相关工作可见,大多数研究将柔性连杆简化为悬臂梁或简支梁,将柔性关节简化为线性扭簧和两个刚性关节,如图1所示.研究表明上述简化是合理有效的,但是它仍然有一些缺点.例如,为了描述关节的柔性,一个虚拟的刚性关节被引入到模型中,这增加了系统的自由度.此外,这种简化方式导致无法通过解析计算来得到系统的模态和频率.这两个缺点使得基于上述简化所建的动力学模型不适合用于控制器设计.为了克服这些问题,本文提出了一种新的柔性关节柔性连杆系统的简化方式:
1.将关节的柔性视作柔性杆的一个弹性约束;
2.柔性杆简化为一个单边弹性约束的简支梁,如图3所示,其中k为扭簧的刚度;
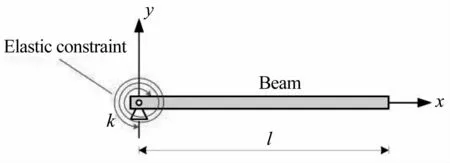
图3 单边弹性约束的柔性连杆模型Fig.3 Model of the flexible link with an elastic constraint
3.柔性关节柔性连杆系统简化为包含刚性关节和单边弹性约束的简支梁的柔性多体系统.
从上面的介绍可以看出,新的简化方法不需要引入虚拟的刚性关节来描述关节柔性,从而降低了系统动力学模型的自由度.对于具有多个柔性关节的机械系统来说,减少动力学模型的自由度将有助于提高求解效率.不仅如此,减少自由度对于控制器的设计也非常有帮助.此外,具有弹性约束的简支梁可以同时考虑梁和关节的柔性,这有助于分析系统的动力学特性和设计控制器.接下来本节将基于多体动力学理论[22]和哈密顿原理建立柔性关节柔性连杆机械臂的动力学模型,具体建模过程如下.
1.1 系统的运动学模型
如图4所示,电机转子在水平面内绕固定点O旋转,刚性转子与柔性连杆通过柔性关节在O点铰接.O-x0y0为惯性参考系,O-xy为固定在柔性连杆上的浮动参考系,梁的长度为l,电机的转角为θ,电机上的外力矩为τ.
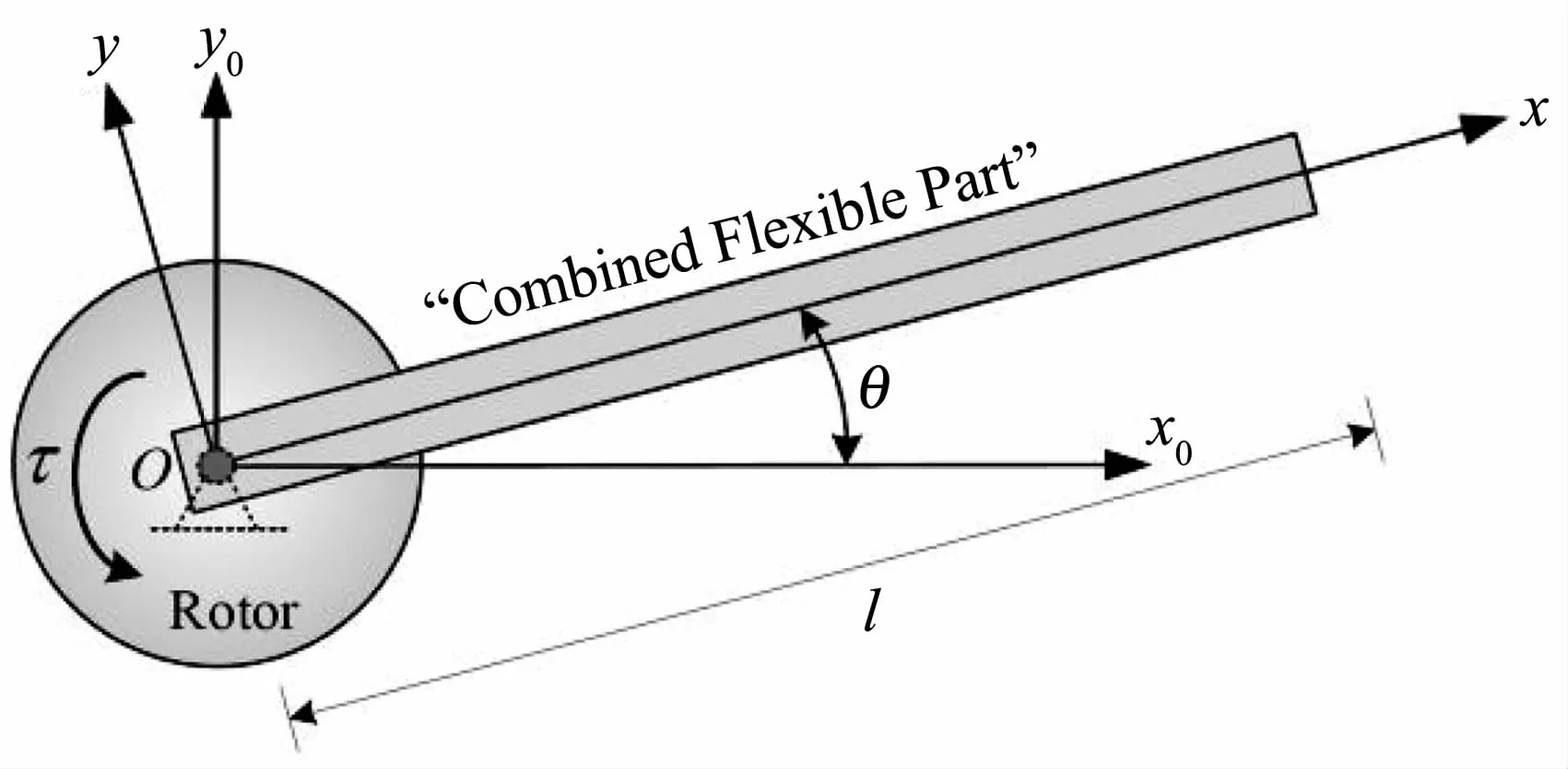
图4 柔性关节柔性连杆系统的结构模型Fig.4 Structural model of the flexible-joint flexible-link system
图5描述了梁上任一点P0的变形,其中,为P0变形前的初始位矢,为变形矢量,变形后P0移动到点P,P点的位矢为

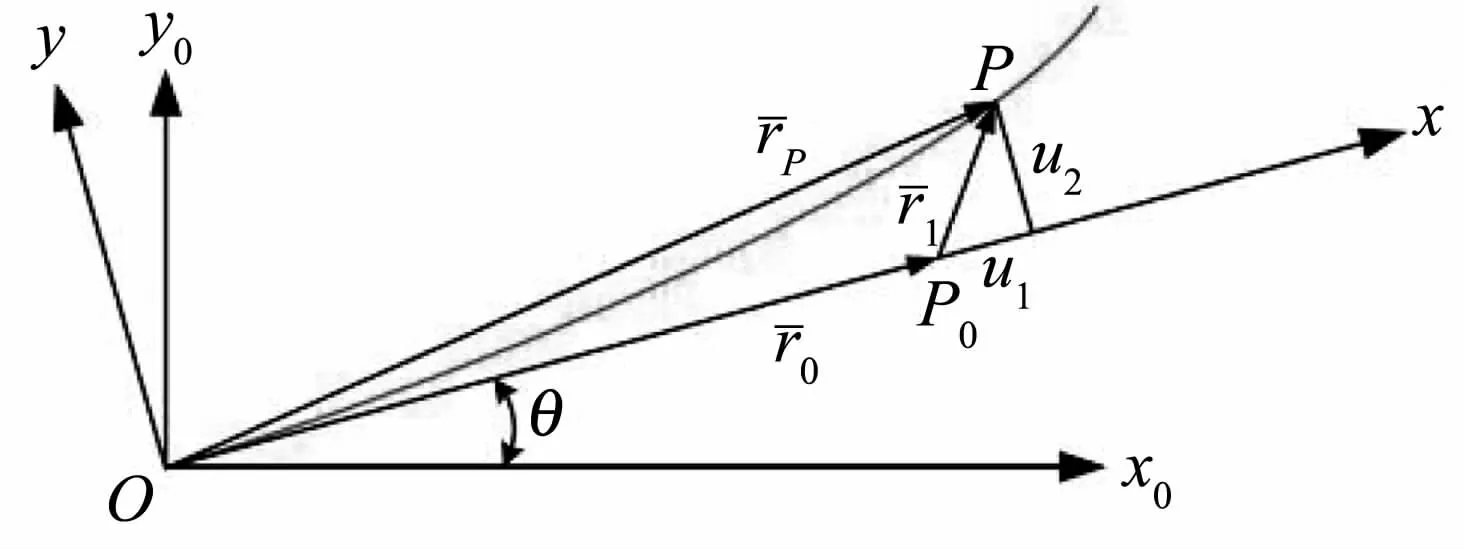
图5 柔性连杆变形的描述Fig.5 Deformation description of the flexible beam

1.2 偏微分形式的系统动力学方程



2 假设模态法离散的动力学方程
动力学方程(18)是时变的非线性偏微分方程,其直接求解的难度是非常大的.通常的求解方法是,首先对原方程对进行离散化处理,将无限自由度系统的偏微分方程转化为有限自由度系统的常微分方程,然后使用数值方法获得系统的近似解.假设模态法是一种比较经典的离散化处理方法,本文将使用该方法对柔性连杆的偏微分动力学方程进行离散化处理.
2.1 模态分析
根据假设模态法理论,首先需要计算柔性连杆的模态函数和振动频率.推导过程如下:
假设图3中的梁为匀质欧拉-伯努利梁,其自由弯曲振动方程为[24]:


由此我们得到了单边弹性约束的柔性连杆自由振动的固有频率(34)和模态函数(35),其有效性在第3.1节进行验证.
2.2 动力学方程的离散化
根据假设模态法理论,考虑关节柔性后的柔性连杆变形可以被离散化为:

计算离散形式的动力学方程时,直接离散偏微分形式的方程通常比较困难,但如果对式(8)、式(14)、式(15)给出的变分项 δT、δH、δWF进行离散,可以降低离散的难度.得到变分项的离散式后,将结果代入哈密顿原理式(6)即可得到离散形式的动力学方程.
将式(37) ~式(42)代入式(14)可得势能变分δH的离散形式:
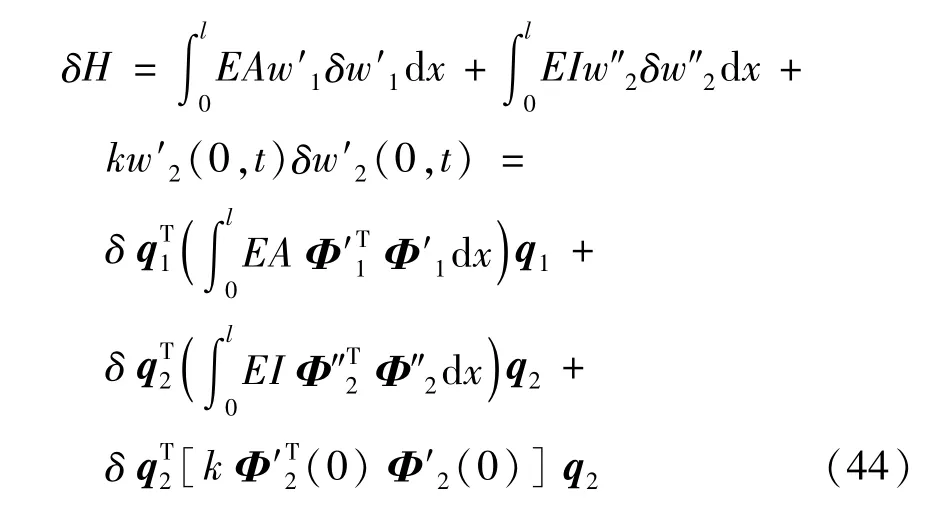
同理将式(37) ~式(42)代入式(8)和式(15)可以得到δT和δWF的离散形式,将离散的结果代入哈密顿原理即得到离散形式的动力学方程:

方程(45)中的阻尼项可以表示为C=CJ+CS,其中CJ为柔性关节阻尼的贡献,CS为梁结构阻尼的贡献,而结构阻尼CS可以通过比例阻尼或瑞利阻尼表示[22].考虑到本文模型中的刚度矩阵受到卷簧的影响,所以选择关于质量矩阵的比例阻尼来计算结构阻尼,阻尼矩阵的表达式为:
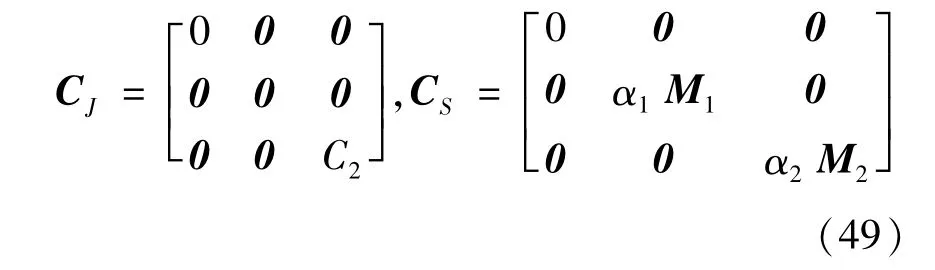
其中,α1和α2分别为轴向和横向振动的阻尼系数,另外由上文的推导可得
至此,我们得到了离散形式的柔性关节柔性连杆机械臂系统的动力学方程,该方程可以通过多种数值方法进行求解.
3 数值仿真
本节将通过数值仿真验证前面给出的理论推导的正确性并检验本文所给出方法相对传统方法是否具有优势.
3.1 与ANSYS软件对比模态分析结果
本文在2.1节给出了具有弹性约束柔性连杆的频率和模态计算过程,现在将通过软件仿真来验证推导结果的正确性.首先,采用本文给出的推导结果计算图3所示具有弹性约束的柔性连杆的频率和模态(分别如表2和图6所示),系统的参数如表1所示.然后,在ANSYS软件中计算该系统的模态和频率,得到的频率结果如表2所示,模态函数如图6.观察表2和图6可得,本文方法的计算结果与ANSYS软件的计算结果是比较吻合,这证明了我们的方法是有效的.

表1 圆截面匀质梁的参数Table 1 Parameters of a uniform beam with a circular cross-section
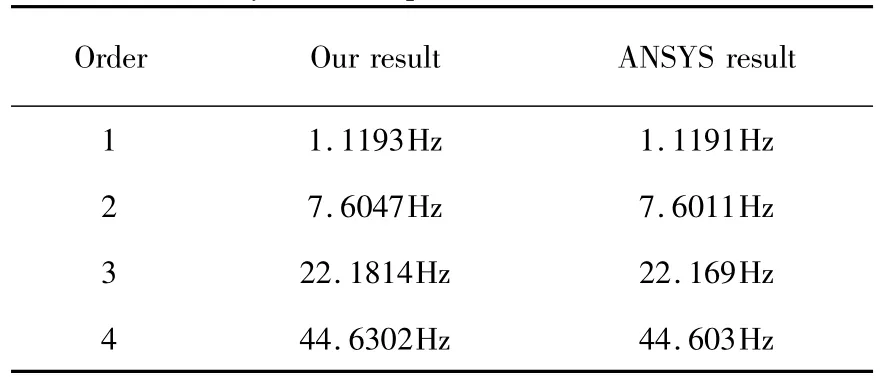
表2 模态分析结果与ANSYS对比Table 2 Modal analysis results of the FLFJ system compared to ANSYS
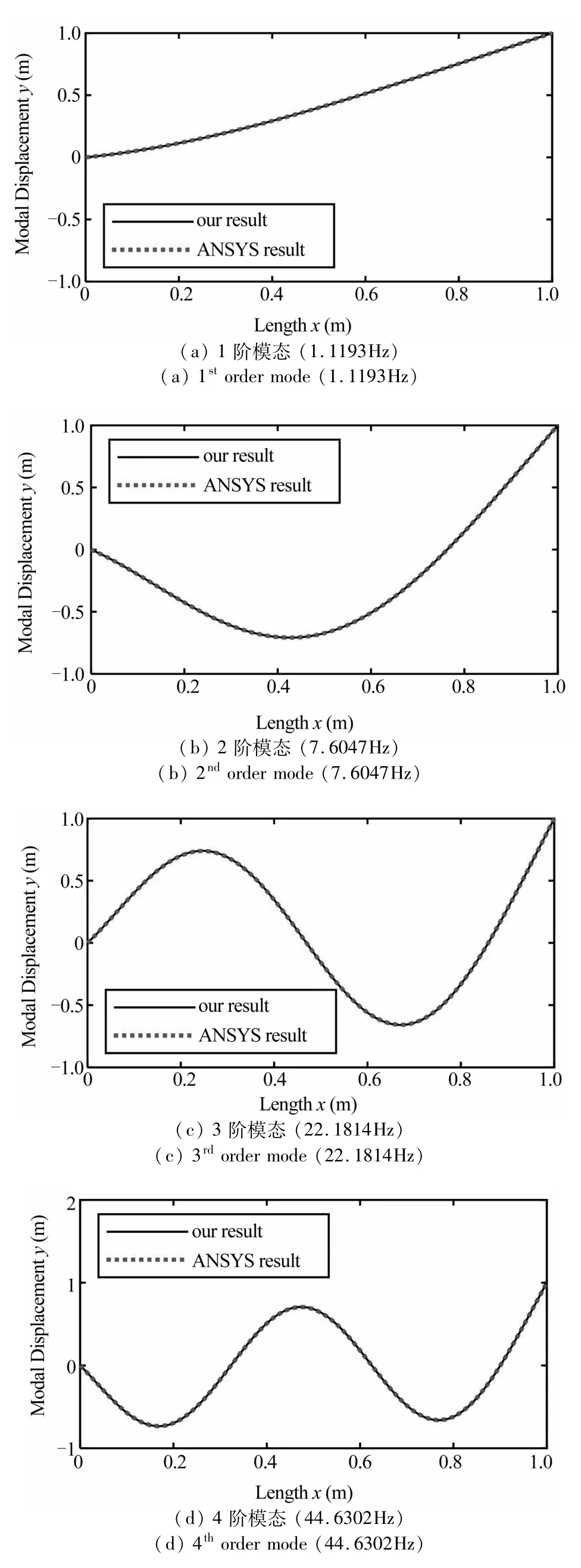
图6 模态函数形状与ANSYS对比(归一化后)Fig.6 Mode shapes of the FLFJ system compared to those of ANSYS
3.2 与ADAMS软件对比动力学仿真结果
在本小节,本文提出的方法和传统建模方法都将用于建立图2所示系统的动力学模型,然后通过仿真结果对比来验证本文方法的有效性.为了让对比更加精确,我们采用ADAMS软件来建立基于传统方法的柔性机械臂动力学模型.在ADAMS软件建模中,将柔性关节简化为两个刚性关节和一个扭簧,连杆的参数与表1相同,转子的转动惯量为0.002kg·m2,分别在三种不同的参数条件下(柔性关节的阻尼和驱动力矩不同,见表3)进行动力学仿真.接着,在同样的参数条件下,采用本文方法建模并编程进行仿真计算,将我们的仿真结果与ADAMS对比(如图7),可以看出我们模型的结果曲线与ADAMS模型的结果曲线完全一致,也就是说,本文提出的建模方法是正确有效的.

表3 仿真时使用的力矩和阻尼参数Table 3 The simulation results comparing our proposal with ADAMS model
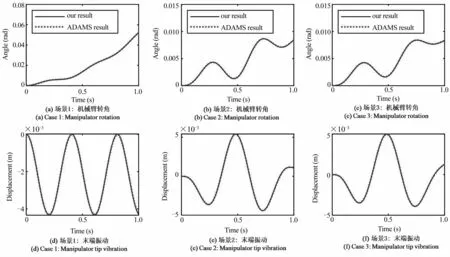
图7 与ADAMS软件对比仿真结果Fig.7 The simulation results comparing our proposal with the ADAMS model
3.3 柔性关节参数对系统动力学特性的影响
如引言所述,关节柔性对柔性机械臂系统的动力学特性有很大影响,本节将从多角度探讨这种影响.由式(32)和式(34)可见,柔性关节柔性连杆机械臂系统的固有频率是关于关节刚度和柔性连杆结构参数的函数.将不同的关节刚度代入式(32)和式(34),即可解得系统的固有频率,如表4所示.观察该表可得,系统的固有频率会随着关节刚度的增加而增加.当k趋近于无穷大时,系统的频率与悬臂梁的频率(表5)相同.
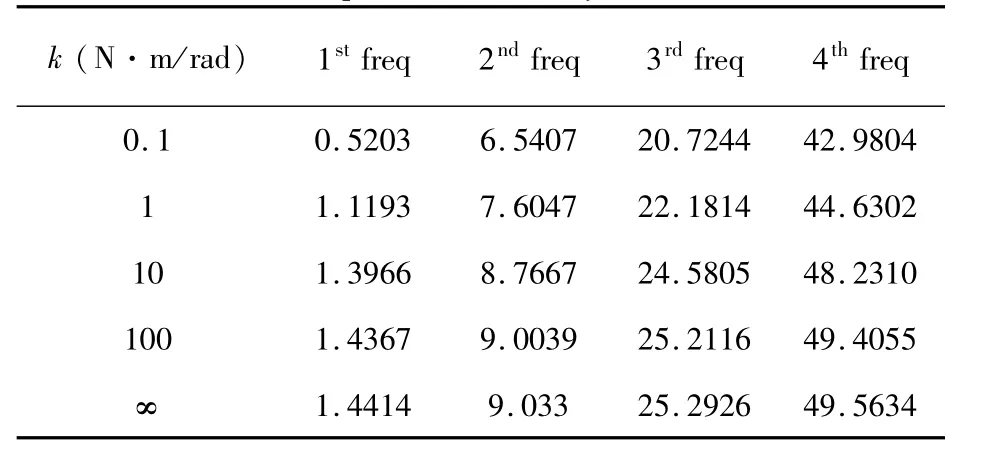
表4 关节刚度对系统固有频率的影响 (单位:Hz)Table 4 The influence of the stiffness on natural frequencies of the system

表5 悬臂梁的固有频率(单位:Hz)Table 5 The natural frequencies of the cantilever beam
以上结果表明,关节的刚度较小时,关节柔性对系统的动力学特性有很大的影响,这引发了我们的思考:在实际工程应用中,关节刚度与柔性连杆的结构参数满足什么样的条件时,关节可以看作是刚性的?换句话说,工程上需要一个准则来判断是否需要考虑关节柔性.我们认为这是值得深入研究的问题.下面,本小节将采用柔性关节机械臂系统与悬臂梁的一阶固有频率的比值r来判断关节是否可以视作刚性,具体准则如下.
准则1.如果r大于临界值rc,关节可以视作刚性.
当r=rc时,相应的关节刚度k称为临界刚度kc.

即比值 r为 n和 k的非线性函数.分别令 n为0.0813、0.1626、0.3252,r关于 k的曲线如图 8 所示.观察该图可见,r为关于k的单调递增函数,即随刚度k增大而增大.这表明当k大于kc时,r一定大于rc.根据准则1,此时可以忽略关节的柔性.因此,当rc给定时,用相应的kc就可以判断是否可以忽略关节柔性.下面,本小节将给出kc的计算过程.
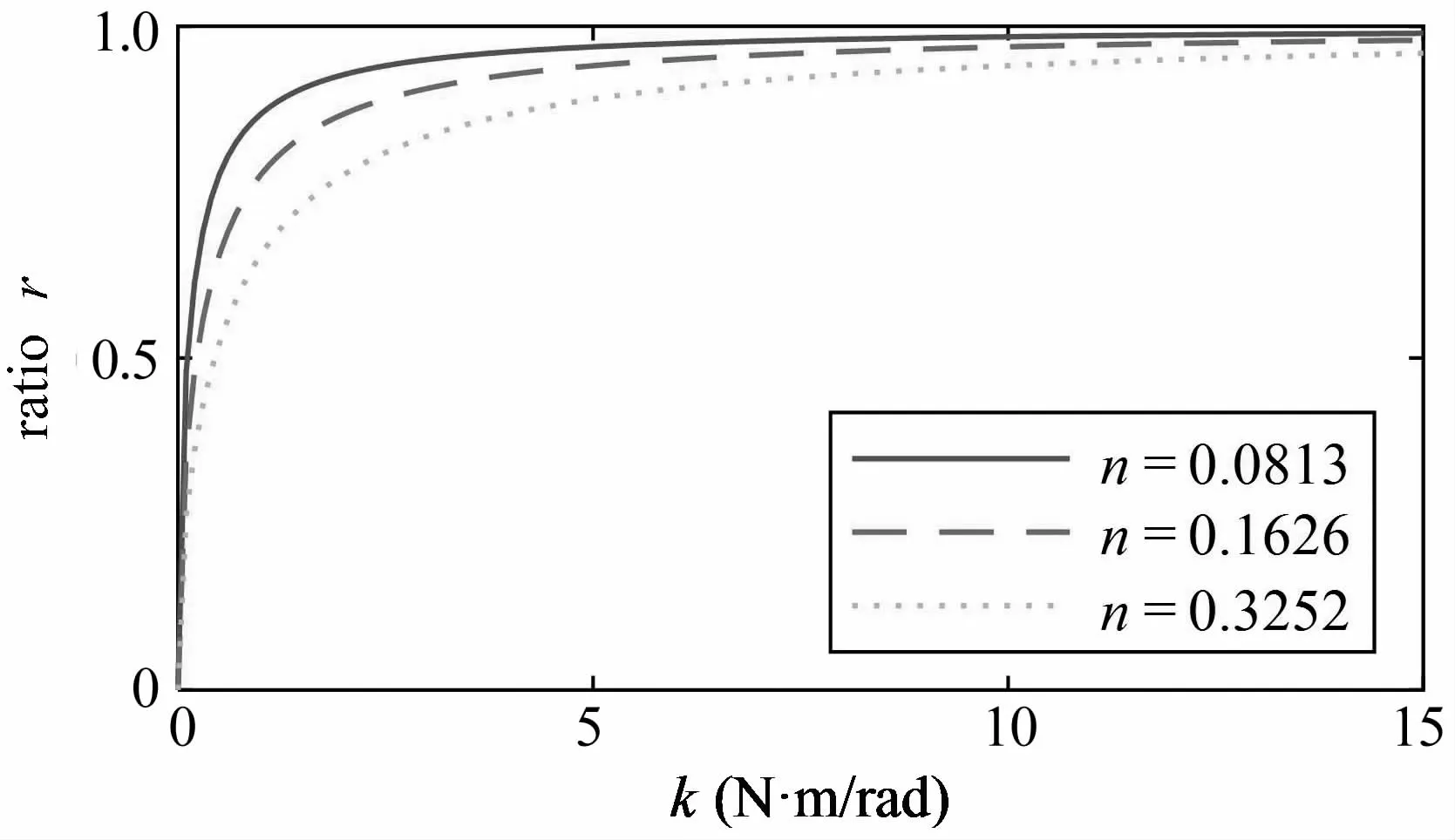
图8 不同梁参数下,频率比和关节刚度的关系Fig.8 The ratio of the frequencies with different parameters
分别令 rc为 0.95、0.97、0.99,临界刚度 kc与梁参数n的关系如图9所示,可见kc为关于n的线性函数,表达为:

其中,P为与rc有关的系数,图9中的P值分别为37.1361、63.8008、197.1245.通过数值计算可以得到P与rc的关系,如图10所示,P为关于rc的非线性函数.根据图10的结果和式(55),很容易计算不同柔性连杆结构参数下的临界刚度kc,例如,对于仿真使用的柔性关节机械臂系统,当rc取0.95、0.97、0.99时,相应的临界刚度kc如表6所示.
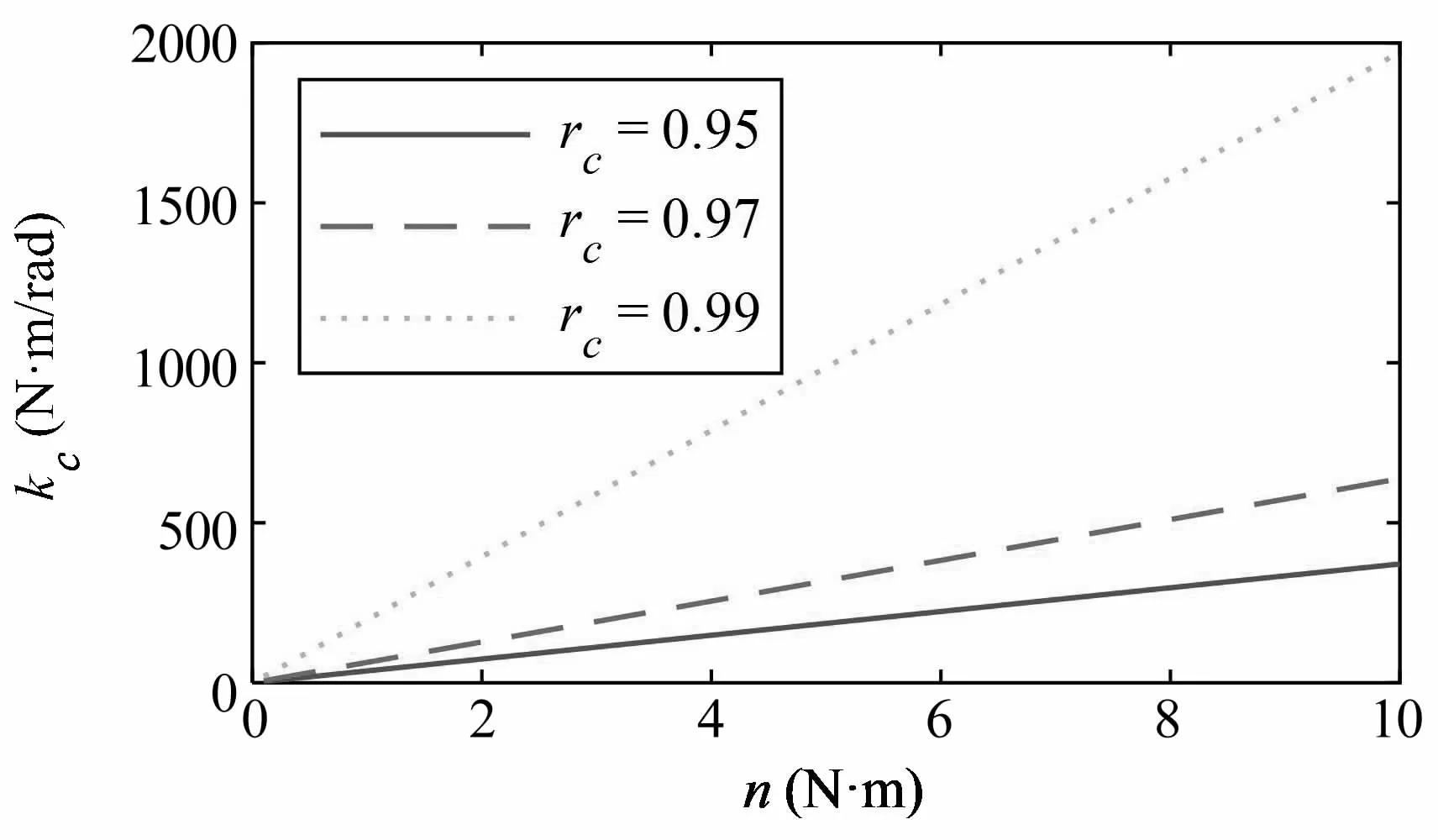
图9 不同rc时,临界刚度kc与梁参数n的关系Fig.9 The kc-n relation for different rc

表6 不同rc时,柔性关节机械臂系统的临界刚度kcTable 6 Corresponding kc values of the system for different rc
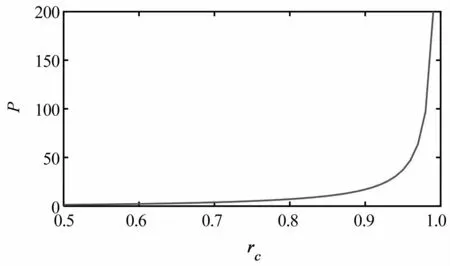
图10 P与rc的关系Fig.10 The P-rc relation
3.4 运动控制仿真结果
本小节将通过控制仿真实验来验证本文给出的模型更适合用于运动控制,由于机械臂系统存在柔性,因此系统在运动过程中难免产生振动,为了实现高精度的控制,在设计控制器时需要采用一种具有振动抑制功能的控制方法.考虑到在第2.1节已经得到了系统的振动频率,因此采用输入整形控制方法[25]是个不错的选择.附录给出了输入整形控制方法的具体形式.
下面将进行两组仿真,以验证本文提出的动力学模型更适合做运动控制设计.仿真中分别使用本文模型和文献[21]中的模型设计ZVD输入整形器和PD控制器.文献[21]在建模时使用Spong模型描述柔性关节,并将柔性连杆视为悬臂梁.在两组仿真中,均设计四种场景,控制柔性关节机械臂系统在1s、2s、3s、4s内旋转1rad,相应的控制信号如图11 所示,PD控制器的参数均为Kp=0.6,Kd=0.3.
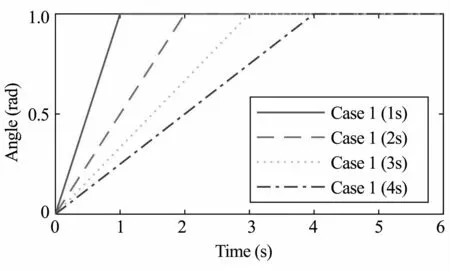
图11 四种场景的初始控制信号Fig.11 The initial angular control signals for 4 cases
在第一组仿真中,柔性关节的刚度k为1N·m/rad,分别使用本文模型和文献[21]中的模型,选取前四阶模态设计ZVD输入整形器,相应的模态频率和ZVD参数见表7.仿真时使用ZVD整形器和PD控制器来控制系统运动并同时抑制振动,仿真结果见图12~图15,其中图12(a)~图15(a)为系统旋转角度的时间历程,图12(b)~图15(b)为机械臂末端变形的时间历程,图12(c)~图15(c)为电机控制力矩的时间历程.观察图12(a)~图15(a)可以看出,基于两种模型的控制器都可以让系统到达目标位置,但使用文献[21]中的模型设计控制器可以使系统更快地到达所需的旋转角度,这是因为本文模型的固有频率低于悬臂梁的固有频率,见表7,根据输入整形方法,控制过程所需时间随着系统频率的降低而增加.因此,文献[21]中的模型可以使系统更快地到达所需的旋转角度.但是对于柔性机械臂来讲,机械臂的末端到达指定位置并停止振动所花费的时间也是衡量控制效果好坏的重要指标,因此,更快地到达所需的旋转角度并不意味着控制器的性能更好.观察图12(b)~图15(b)可以看出,基于本文动力学模型的控制器可以更快地消除柔性系统的振动,这意味着使用本文模型设计的控制器具有更好的振动抑制性能.观察图12(c)~图15(c)可见,使用本文模型的控制力矩曲线更为平滑,对控制的要求更低.
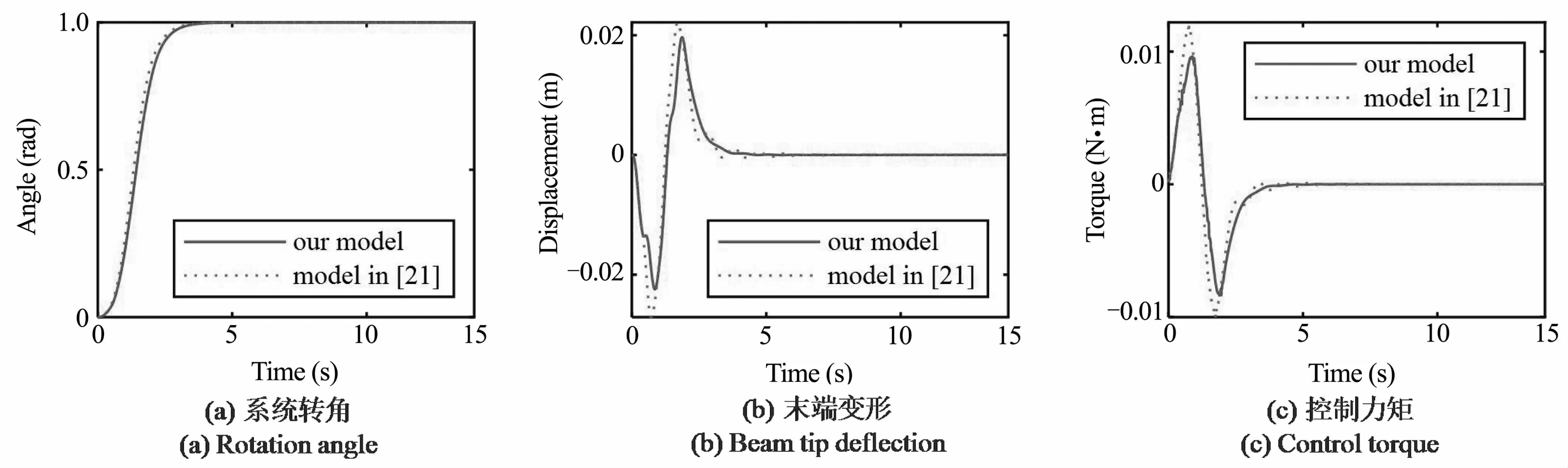
图12 k=1N·m/rad时场景1(1s)的控制结果Fig.12 Control results for case1 (1s) when k=1N·m/rad

表7 k=1N·m/rad时系统的固有频率和ZVD整形器参数Table 7 The frequencies of the system and ZVD parameters when k=1N·m/rad
在第二组仿真中,柔性关节的刚度k为0.1N·m/rad,分别使用本文模型和文献[21]中的模型,选取前四阶模态设计ZVD输入整形器,相应的模态频率和ZVD参数见表8.仿真时使用ZVD整形器和PD控制器来控制系统运动并同时抑制振动,仿真结果见图16~图19.可以看出,基于本文所设计的控制器可以取得更好的控制效果.此外,对比两组仿真可以看出,关节的刚度越小,基于本文模型的控制器在控制性能上的优势越大.
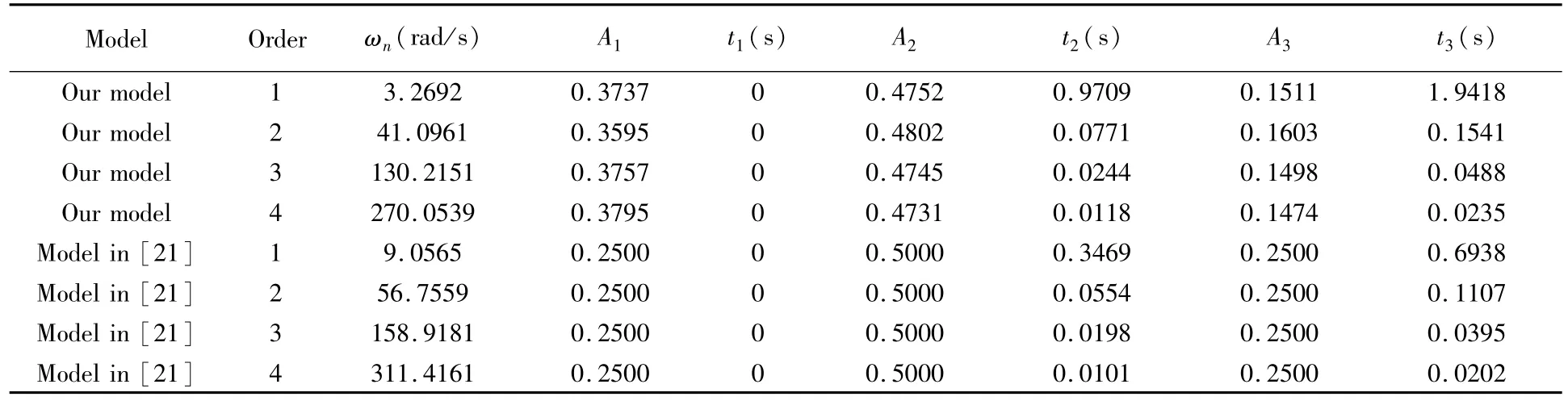
表8 k=0.1N·m/rad时系统的固有频率和ZVD整形器参数Table 8 The frequencies of the system and ZVD parameters when k=0.1N·m/rad
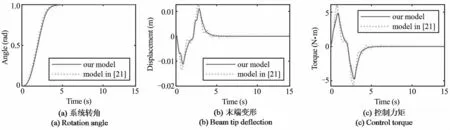
图13 k=1N·m/rad时场景2(2s)的控制结果Fig.13 Control results for case 2 (2s) when k=1N·m/rad
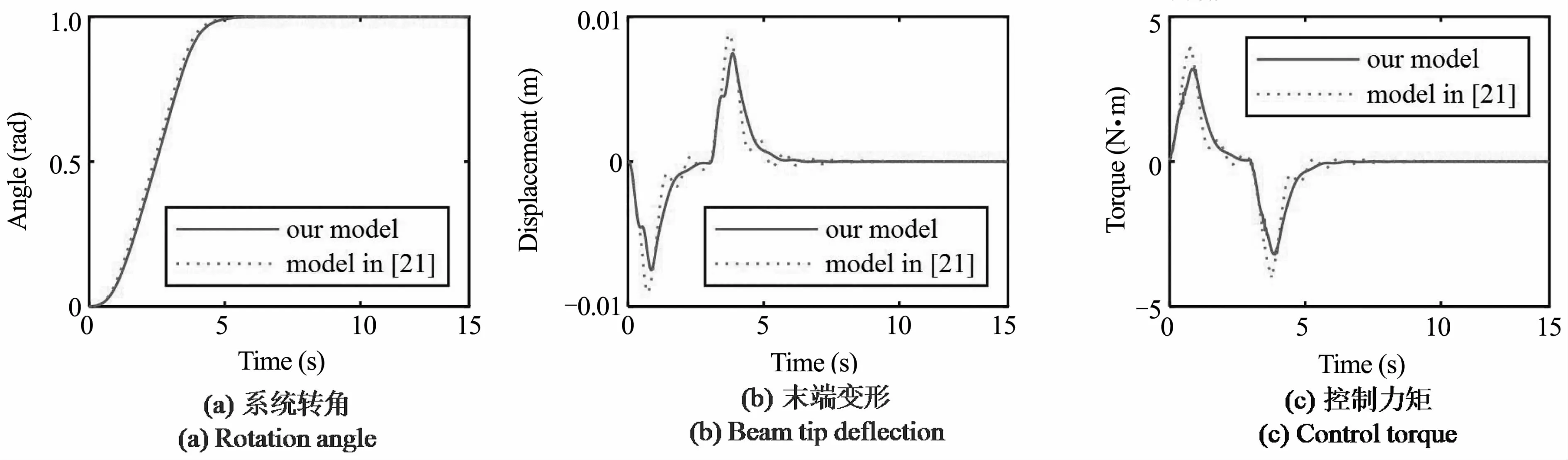
图14 k=1N·m/rad时场景3(3s)的控制结果Fig.14 Control results for case 3 (3s) when k=1N·m/rad
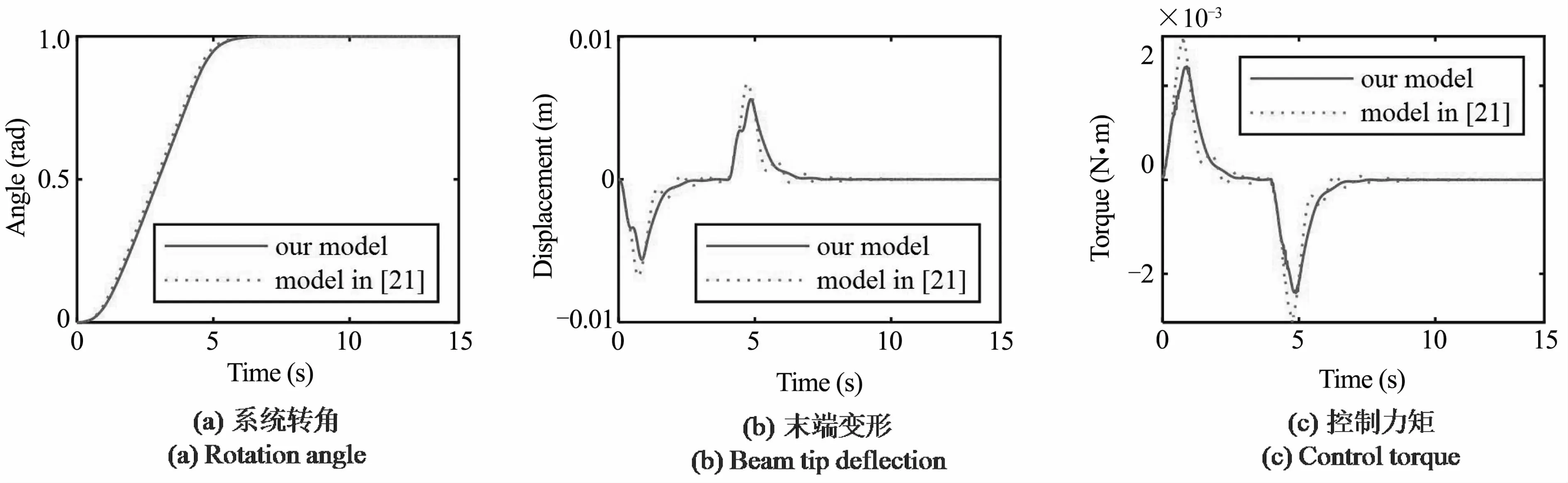
图15 k=1N·m/rad时场景4(4s)的控制结果Fig.15 Control results for case 4 (4s) when k=1N·m/rad
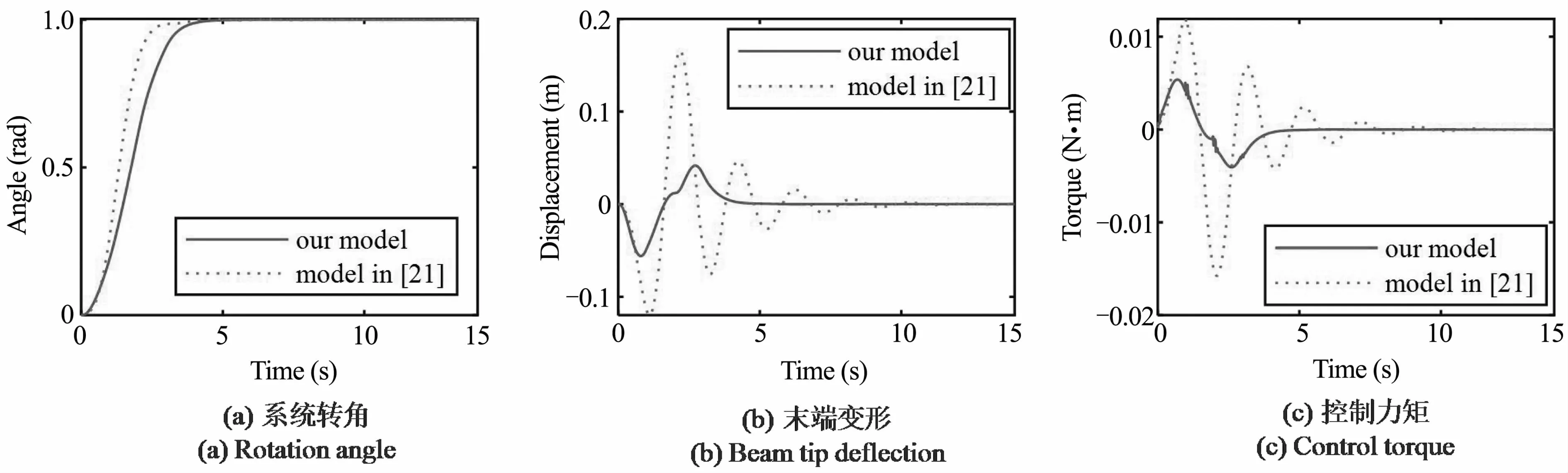
图16 k=0.1N·m/rad时场景1(1s)的控制结果Fig.16 Control results for case 1 (1s) when k=0.1N·m/rad
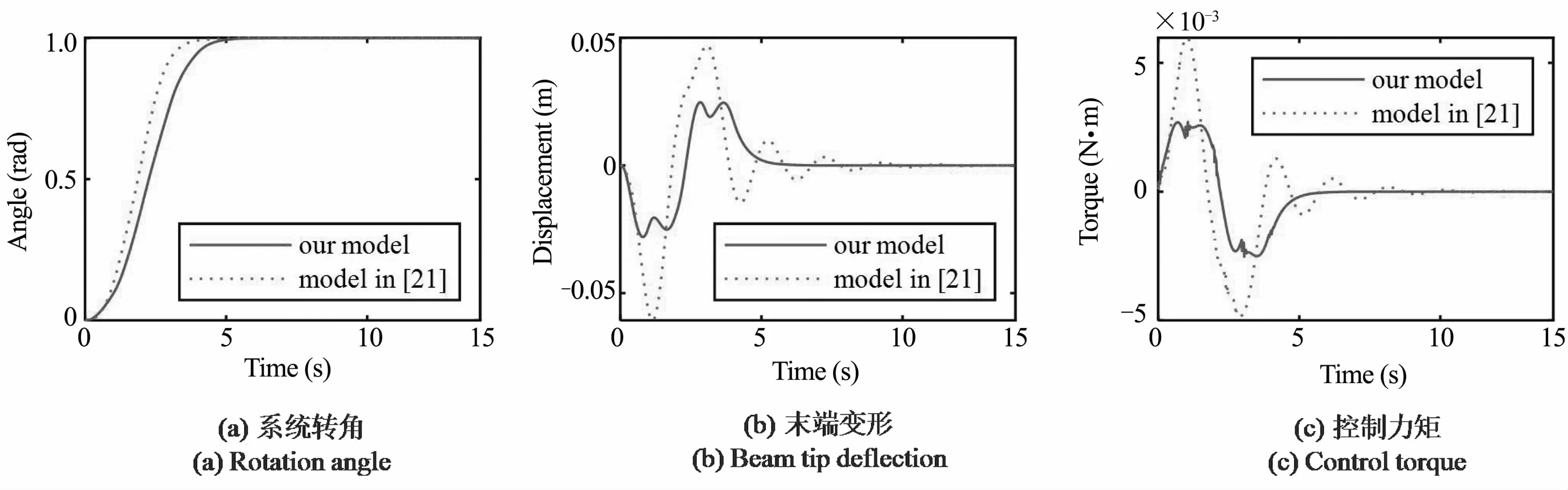
图17 k=0.1N·m/rad时场景2(2s)的控制结果Fig.17 Control results for case 2 (2s) when k=0.1N·m/rad
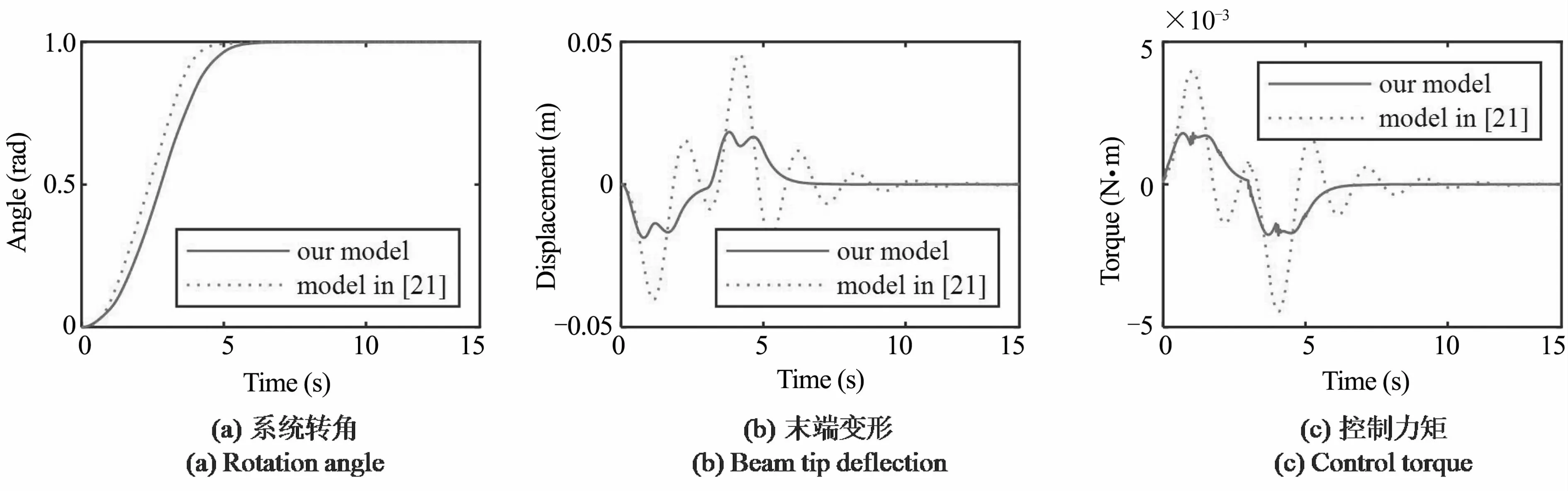
图18 k=0.1N·m/rad时场景3(3s)的控制结果Fig.18 Control results for case 3 (3s) when k=0.1N·m/rad
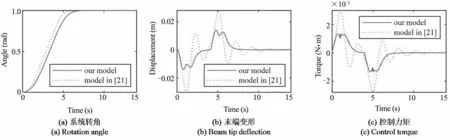
图19 k=0.1N·m/rad时场景4(4s)的控制结果Fig.19 Control results for case 4 (4s) when k=0.1N·m/rad
4 结论
本文研究了柔性关节柔性连杆机械臂系统的动力学建模问题,并提出了一种改进的建模方法.在该方法中,连接柔性连杆的柔性关节首先被简化为刚性关节和柔性连杆的弹性约束边界.然后,根据结构动力学理论、哈密顿原理和假设模态法建立系统的刚柔耦合动力学方程.与传统模型相比,新模型不仅具有更少的自由度数,还可直接描述关节柔性和连杆柔性的耦合作用,这对于进行系统的动力学特性分析和控制器设计是非常有利的.在数值仿真部分,本文方法的有效性首先被验证.然后,基于本文方法所建模型在分析和控制上的优势也得到了充分的证明.由此可见,本文所给出的建模方法相对传统建模方法具备明显优势.

