基于降阶自抗扰的永磁同步电机位置控制*

高旭生，李 娟，李生权，李 喆，冯 波

(扬州大学电气与能源动力工程学院，扬州 225127)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)因其易于集成、效率高、稳定性好等优良特性，在轨道交通、工业机器人、新能源汽车等领域中得到大量应用[1]。随着其应用领域的拓展，现代工业应用中对位置伺服系统的定位精度、响应速度等性能的要求日趋提升，进而推动PMSM位置高精度控制的研究[2]。

传统PMSM位置控制中主要应用PI控制器，其算法简单且易于实现。但PMSM位置控制系统运行过程存在诸如转动惯量变化、定子电阻改变等内部参数摄动和不可测干扰，基于误差控制的PI控制方式调节范围有限，难以实现PMSM的高精度定位控制[3]。近年来，很多现代控制方法逐步应用于PMSM高精度定位控制领域，如模型预测控制、迭代学习控制、滑模控制等[4-6]。然而这些先进控制策略往往会存在算法复杂、依赖模型、参数众多或抖振等局限性，导致此类先进控制策略在工业上难以推广应用[7]。

自抗扰控制(active disturbance rejection control,ADRC)不依赖系统模型信息，算法易于实现，通过扩张状态观测器(extended state observer,ESO)来观测系统的内外干扰并加以补偿，因而拥有优异的动态响应能力、静态性能。因而，一些学者将ADRC应用于永磁同步电机控制领域[8]。邱建琪等[9]针对控制周期长、时延较大的应用条件下PMSM定位控制效果较差的问题，将ADRC引入位置控制中，通过ESO观测干扰并进行补偿，有效提高了位置控制的定位精度。左月飞等[10]针对位置-电流双环结构系统响应性能与速度超限的问题，将线性扩张状态观测器(LESO)与滑模控制相结合，通过速度限幅，提升了系统动态性能。LIU等[11]针对传统三环位置控制定位精度受限、指令响应速度受串级结构影响，基于非线性ADRC提出一种PMSM双环位置控制结构，提高了位置控制的鲁棒性能，但非线性ARDC调参较为复杂。

然而，上述文献聚焦于ADRC对PMSM位置控制系统抗扰性能的提升，而ESO观测能力对系统性能影响研究较少。在ADRC控制理论中，ESO的阶次高系统一阶，必然导致相位滞后，进而导致系统的控制性能降低[12]。在系统输出及其多阶导数可以借助传感器和计算获得时，可以采用对ESO降阶的方法，削弱相位滞后，降低干扰估计的计算量，提高干扰估计的精度和速度[13]。因此，本文提出一种基于降阶扩张状态观测器(reduced-order extended state observer,RESO)的PMSM定位控制方法，该方法联系工程实际，考虑脉冲指令给定方式对系统建模的影响，重构系统状态方程，设计RESO对PMSM位置控制中的内、外干扰进行观测，省去对已知状态量的重复观测，改善控制器性能，并给出控制器的稳定性证明。最后，通过仿真与实验对PMSM降阶自抗扰位置控制方法的指令跟随性能和稳态性能进行验证。

1 PMSM数学模型

在d-q坐标系下，且采用id=0的控制策略时，PMSM的电磁转矩为：

Te=1.5pn(ψr+(Ld-Lq)id)iq

(1)

式中，Te为电磁转矩；pn为电机极对数；ψr为转子磁链；Ld、Lq分别为直轴电感、交轴电感；id、iq分别为直轴电流、交轴电流。

运动方程为：

(2)

式中，TL为负载转矩；J为转动惯量；ωm为机械角速度；B为粘滞摩擦系数。

PMSM转子的机械旋转角度θ、给定位置指令脉冲数θp与电机机械角速度之间的关系近似为：

(3)

式中，PPR为电机旋转一圈，编码器输出的脉冲数。

然而，实际应用中的伺服系统是一个多变量、强耦合的非线性系统，其控制效果受到运行中多种因素的约束，比如负载的变化、实际参数摄动、静摩擦等。因此，在位置环的控制中需要体现出这些因素的影响，式(3)可改写为：

(4)

2 位置环降阶自抗扰控制器设计

2.1 降阶扩张状态观测器设计

(5)

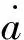
根据Luenberger状态观测器的通用设计原则，设计二阶LESO：

(6)

式中，z1、z2分别为状态量θp、a的观测值；β1、β2为观测器增益。

根据文献[14]，通过配置极点，设计LESO的增益如下：

(7)

式中，p为观测器带宽，p>0。

对于一阶的系统，通常采用二阶ESO观测系统的干扰。在PMSM位置控制中，电机旋转角度的脉冲数pulse和机械角速度ωm可通过增量式旋转编码器实时获取计算得到，且位置环作为电机控制最外层的环节，引入的高频噪声对系统影响有限，本文旨在降低干扰观测器算法的运算量，提高干扰估计的快速性和准确性，引入降阶扩张状态观测器(RESO)。由式(7)得：

(8)

定义状态变量：

(9)

根据文献[15]，设计降阶观测器如式(10)所示。

(10)

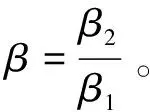
定义状态变量：

z=zt1-βθp

(11)

结合式(10)、式(11)，推出降阶扩张状态观测器方程如下：

(12)

观测的综合干扰为：

zt1=z+βθp

(13)

假设干扰及干扰的微分有界，定义RESO干扰估计误差ε为：

ε=zt1-a

(14)

对式(14)两侧求导得：

(15)

结合式(12)、式(13)，得：

(16)

代入式(5)，得：

(17)

因为干扰及干扰的微分有界且β>0，所以RESO收敛，t→∞，观测误差ε→0。

2.2 误差反馈控制律设计

将式(4)设计为：

(18)

式中，u0为控制律。

在降阶扩张状态观测器可以准确且快速的观测出总干扰时，结合式(4)、式(18)得：

(19)

最终，结合RESO设计的复合控制律如下：

(20)

2.2.1 控制器稳定性分析

定义控制器跟踪误差：

(21)

选取李雅普洛夫函数：

(22)

则有：

(23)

定义有限时间函数：

(24)

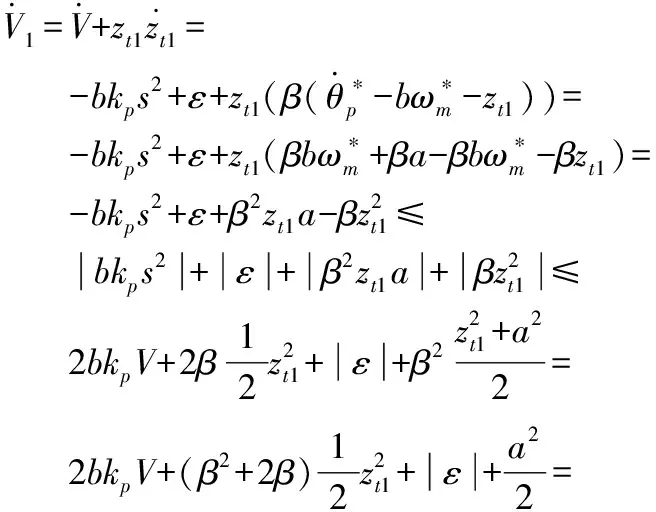
(25)

式中，

(26)

(27)

式(26)、式(27)都是大于0的有界常数，根据文献[16]在干扰不发生改变的情况下，闭环系统不会在有限时间内发散，当干扰的估计误差逐渐趋近于0，此时式(23)转化为：

(28)

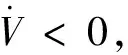
3 仿真研究

为验证本文提出控制策略，在MATLAB的Simulink环境中搭建PI控制三环定位模型、位置环改进自抗扰定位模型与位置环改进降阶自抗扰定位模型进行对比验证。仿真及实验所用的PMSM的参数如表1所示。基于位置环降阶自抗扰控制结构如图1所示。

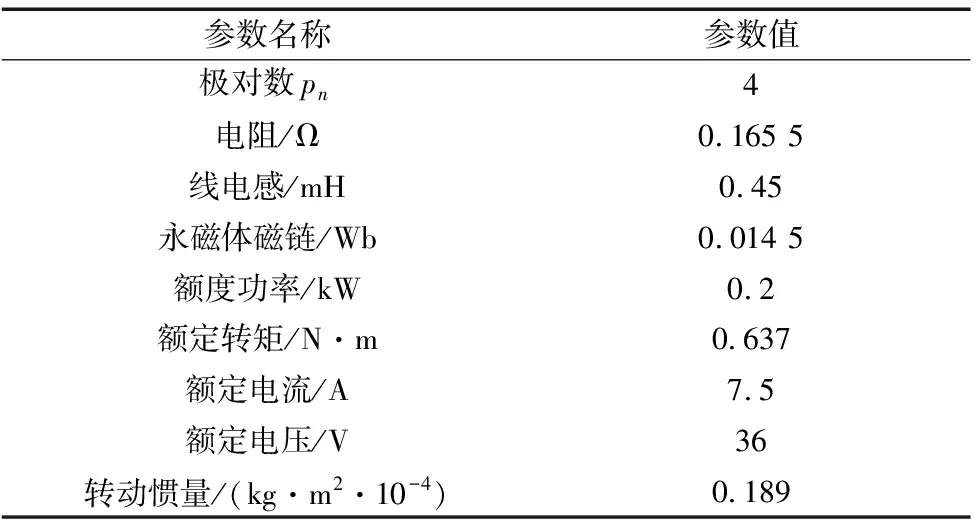
表1 PMSM参数

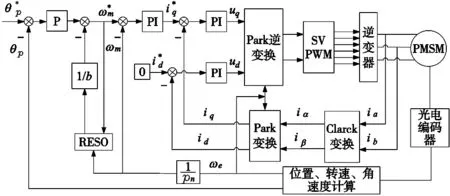
图1 系统控制框图

在无负载干扰的仿真条件下，初始目标位置脉冲数为20 000，在0.4 s时刻目标位置脉冲数变更为50 000，3种控制方式仿真运行的位置跟随、速度响应和交轴电流变化分别如图2、图3和图4所示。

图2 位置响应曲线 图3 速度变化曲线

图4 交轴电流变化曲线

由图2位置响应曲线可见，脉冲数20 000阶跃给定时，RESO控制的位置响应上升时间为36.3 ms、调节时间为60.8 ms，LESO控制的位置响应上升时间为47.5 ms，调节时间73.27 ms，PI控制的位置响应上升时间41.8 ms，调节时间为83.9 ms。脉冲数50 000阶跃给定时，RESO控制的位置响应上升时间为49.9 ms、调节时间为70.4 ms，LESO控制的位置响应上升时间为50.8 ms，调节时间73.8 ms，PI控制的位置响应上升时间53.6 ms，调节时间为85.9 ms，即阶跃位置给定条件下RESO位置控制在上升时间、调节时间指标均优于LESO位置控制和PI位置控制，动态性能更好。此外，RESO和LESO位置控制可以实现无超调的准确定位，稳态性能优于存在±3脉冲波动的PI位置控制。由图3速度变化曲线可知，阶跃位置给定条件下，3种位置控制方式均会不同程度的导致转速超限，基于LESO位置控制在阶跃给定20 000脉冲时超限约9%，而阶跃给定50 000脉冲时与当前值较大时超限与PI位置控制相近超限17%，RESO位置控制速度超限最小，约为4%，此外，RESO和LESO位置控制进入稳态后速度波动低于PI位置控制进入稳态后的速度波动。由图4中交轴电流变化曲线可看出，阶跃位置给定时，基于RESO位置控制的交轴电流峰值较另外两种方式显著降低，且稳态性能良好。

4 实验验证

为验证本文提出的基于降阶扩张状态观测器的自抗扰位置控制策略的有效性和优越性，搭建实验平台如图5所示。实验平台的主体由上位机、永磁同步电机、电力电子开发平台、DSP(F28335)、仿真器、直流稳压稳流电源模块组成。实验电机参数与仿真参数一致。

图5 实验平台

在空载电机位置控制实验中，为了便于实验数据采集，速度环输入设限为±200 rpm。t=5 s时给定目标位置为pulse=20 000，在t=10 s时刻目标位置为pulse=50 000，位置环基于RESO的自抗扰控制、LESO的自抗扰控制和PI控制器的位置响应曲线、速度变化曲线和交轴电流波形分别如图6～图8所示。

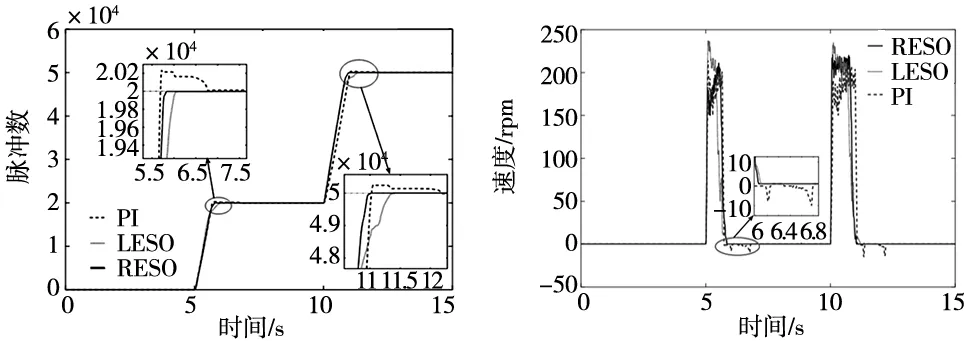
图6 位置响应实验位置变化曲线 图7 位置响应实验的速度变化曲线

图8 位置响应实验的交轴电流变化曲线

由图6的位置响应曲线图可见，在20 000脉冲和50 000脉冲的阶跃目标给定下，3种位置控制器均可达到目标位置的2%误差范围内，且保持稳定运行。PI位置控制器在给定位置为20 000脉冲时，响应性较好，但带来了200脉冲的位置过冲,这也导致了图7中电机反转消除超调后，才达到目标位置。基于RESO的位置控制器与基于LESO的位置控制器，均可实现无超调的精确定位。在目标位置为50 000脉冲时，RESO位置控制器的快速性显著优于另外的两种方式，且由图7可见速度平稳性更优。由图8的交轴电流变化曲线可知，基于RESO的位置控制方式下，交轴电流幅值显著低于其它两种方式，且平稳性更好。综上所述，在PMSM位置控制系统中，基于RESO的位置控制器易于获得较高的定位精度、较快的响应速度、良好的速度平稳性，提高了系统的动、静态性能。

5 结论

本文以永磁同步电机为研究对象，改进传统位置环，提出基于RESO的自抗扰位置控制策略，设计永磁同步电机定位控制系统。主要工作如下：

(1)基于实际应用，重构永磁同步电机的状态方程。

(2)根据脉冲给定设计位置系统中的RESO，对系统的内、外干扰进行估计和补偿，提升了干扰估计的快速性和准确性，进而改善系统的动态性能。

(3)基于RESO构建位置自抗扰控制器，并分析系统的稳定性，借助仿真和实验验证了RESO自抗扰控制器较LESO自抗扰位置控制器和传统PI位置控制器改善了系统的整体性能。