基于Shannon理论改进的多齿铣削力模型*
刘 洋,关世玺,赵 宏,刘莞尔
(1.中北大学机电工程学院,太原 030051;2.晋西工业集团有限责任公司,太原 030027;3.北京宇航系统工程研究所,北京 100076)
0 引言
切削力预测是机械加工中的重要话题之一,其预测的精准度直接影响工件质量的好坏。目前切削力预测模型主要有平均刚性力静态偏移模型、瞬时刚性力模型、考虑再生效应的动态变形力模型、广义铣削力模型、异形铣刀力模型、机器学习算法等[1]。平均刚性静态偏移模型是从切削过程中能量耗散与金属切除率关系的角度入手,该模型偏静态,不能较好地反映铣削力的变化情况。瞬时刚性力模型将参与切削的铣刀刀刃离散,构成众多切削单元。利用切屑面积与切削力的关系[2]计算出每个单元的切削力并求和,最终得出切削力数值。其缺陷是没有考虑刀具偏移。考虑再生效应的动态变形力模型是将系统大致等效为“弹簧-质量-阻尼”系统[3],其主要用于振颤稳定性的研究。广义铣削力模型[4],利用微分几何理论建立了任意形状铣刀的铣削力模型,并将切削力分解为前后刀面的正压力、摩擦力,由此建立铣刀切削单元上的非线性局部切削力表达式,随后沿刀刃积分并对所有刀齿求和,最终求得铣削力。李振加、张智海等[5-6]改进了波形刃铣刀片铣削力模型,为波形刃的优化设计提供理论依据。LI等[7]利用Z-MAP法改进了铣削力模型。CAI等[8]通过有限元法以及NURBS基样条建立了切削力预测模型。LIANG等[9]建立了切削振动情况下的铣削力动态模型。DING等[10]通过剪切区域摩擦角建立了铣削力模型。LIU等[11]基于曲面响应法建立了多齿端面时空域铣削力模型。随着计算机技术的发展,机器学习算法被大量的应用于数据预测的领域,其中也包括切削加工领域。陈远玲、VAISHNAV、王俊成等[12-14]使用BP神经网络较好地预测了切削力。这种方法的缺点在于其需要大量可靠的实验数据作为支撑。
以上几种铣削力建模方式各有优劣,其中瞬时刚性力模型较为成熟,且被大规模应用及研究。其将刀刃离散的处理方式也可应用于其他铣削力模型中,便于融合改进。这种模型基本结构都来源于KOENIGSBERGER和SABBERWAL的简化模型[15-16],经过多年的研究和发展,最终由RIGELSFORD等[17]给出了瞬时刚性力模型的螺旋槽微元力表达式。文中的铣削力模型也采用了瞬时刚性力模型的基本形态,其是由KLINE等[18-20]在瞬时刚性力模型的基础上改进得到的平均力模型。基于对上述铣削力建模方式的总结可知,绝大多数铣削力模型对单齿铣削力的描述都无法避免对其积分上下限进行多次讨论,这样无疑加大了多齿铣削力模型的构建难度,使其具体表达式形态过于复杂,不利于多齿铣削模型的使用及后续优化。基于此问题,本文中采用shannon定理改进了单齿铣削力模型,使多齿铣削力模型得到了进一步简化,最终有效解决了这一问题。
1 铣削力建模
如图1所示,根据文献[21]可得微元切削力:
(1)
式中,kts、krs、kzs为剪切力切削系数ktp、krp、kzp为犁耕力切削系数;px为每齿进给量;dh为微元高度。

图1 铣削力坐标转换图
将微元切削力公式投影至刀具坐标系xyz可得:
(2)
将式(1)带入式(2)可得:
df=(u1v1+u2v2)dh
(3)
式中,
在金属切削时由于单个刀齿无法一直保持切削状态,由此引入判定函数g(θ);当该齿与工件接触时g(θ)=1,未接触时g(θ)=0,如下:
(4)
式中,θ1为切入角;θ2为切出角。
对式(3)进行积分得:
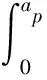
(5)
式中,φ为刀具旋转角;β为刀具端面切削点到刀身切削点的逆时针包角。
根据立铣刀螺旋角与轴向铣削深度的关系可得式(6),式(7):
(6)
(7)
式中,刀具轴向切深为ap;R为刀具半径;α为螺旋角。
刀具旋转一周,刀齿会依次经历A,B,C三种状态,由图2可得f(φ):
(1)ifθ1≤φ≤θ1+β,则:
(8)
(2)ifθ1+β≤φ≤θ2,则:
(9)
(3)ifθ2≤φ≤θ2+β,则:
(10)
(4)其余,则f(φ)=0
由于式(8)~式(10)只适用于单齿切削,现引出多齿切削关系式:
(11)
式中,φi为第i个刀齿的位置角;zp为参与切削的刀齿数目,其有如下关系(以刀具旋转一周为例):
φi=φ-iβ′
(12)
式中,β为齿间角,若φi<0,则该刀齿没有参与切削。

图2 铣削过程展开图
2 基于shannon定理的多齿铣削力模型
由于式(8)~式(11)在实际应用中使用不便,且不利于后续优化。因此,基于shannon理论对该多齿铣削力模型进行拓展,构建出相对简单且有效的多齿铣削力模型。
shannon定理如下:
设信号f(x)∈L2(R),如果存在B>0,使F(ω)=0,|ω|>B,a,e,ω∈R,这里F(ω)是f(x)的傅里叶变换,则称f(x)是B频率截断的,这时,只要采样间隔Δ≤π/B,信号f(x)按间隔Δ进行采样就不会损失信息,且利用采样序列{f(nΔ);n∈Z}可按如下公式构造原信号:
(13)
以下证明式(7)满足shannon定理:
(1)证f(φ)∈L2(R):
由于f(φ)是周期函数,切削力预测只需探讨其单独一个周期的大小,故f(φ)也可表示为如下形式:
if 0≤φ≤2π:
(14)
ifφ<0 orφ>2π:
f(φ)=0
(15)
式中,h1,αp,h2∈a。
由此式(7)满足下式:
(16)
即满足f(φ)∈L2(R)。
(2)证F(ω)=0,|ω|>B,a,e,ω∈R:
提取式(7)中v1、v2,并将其进行傅里叶变换:
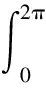
(17)

(18)
由式(17)与式(18)可知,当n越大(即ω越大),v1,v2的值会随之衰减。必然存在一个极大值B,当|ω|>B,使得v1、v2为0,所以可得F(ω)=0。
综上所述,式(7)满足shannon定理使用条件。
为了进一步保证预测精度,遂采用二进shannon法。二进shannon法是shannon基本定理的延伸,适用于|ω|>B,信号不为0的情况,其利用Vk={f(x);F(ω)=0,|ω|>2kπ}子空间,逐步逼近全空间L2(R),即:
(19)
(20)
其中,式(20)根据牛顿莱布尼茨公式可化简为以下形式:
(21)
(22)
(23)
由此可看出,经过shannon定理改进后的单齿铣削力模型得到了巨大的简化,则多齿铣削力模型可直接按式(24)的方式构建:
(24)
可看出,相较于传统多齿铣削力模型,该方法使多齿铣削力模型的构建过程得到了很大程度的简化。
3 MATLAB仿真及铣削力实验
式(21)中存在两个参数k、m(累加上限),即需要找到合适的k、m使得式(21)具有符合要求的预测精度。本文中使用遗传算法对式(21)进行参数寻优。
本文中铣削力模型的建立过程借鉴了文献[22]中单、多齿铣削力模型的建立过程。由于本文中铣削力模型的应用对象与该文献实验中的加工对象相似(具体材料,毛坯与成品形状以及加工方式相似);因此对文献[22]中的实验以及实验数据进行引用,并且MATLAB切削力数值仿真初始条件也与文献[22]实验条件一致。如图4所示,对文献[22]中切削力实验数据进行等间隔采样,将模型预测值与采样值的偏差求和作为目标函数的输出值;将k、m两个参数值作为目标函数的输入值。主体优化思路如图3所示。
在文献[22]中以间隔0.2的方式依次取样,整体取样间隔为2π,如图4所示。

(c) F3数据采样图
以文献[22]中铣削力实验为例,采用4齿直径为12 mm,螺旋角为30°的立铣刀,轴向切深为1 mm,主轴转速为800 r/min,进给量为320 mm/min。并采用其得出的切削力系数如表1所示。通过MATLAB仿真得出最优参数如表2所示。

表1 切削力系数 (N·mm-2)

表2 铣削力优化参数
得出初始铣削力与实验值对比图,如图5所示。

(a) F1初始对比图 (b) F2初始对比图

(c) F3初始对比图
由图可得,模型预测值的变化趋势与实验值基本吻合,但两者存在一个整数偏差;现引进一个修正信号如下:
(25)
(26)
(27)
将修正信号引入,随即得出以下对比,如图6所示。

(a) 修正后F1对比图 (b) 修正后F2对比图

(c) 修正后F3对比图
可看出,引入修正信号后预测效果大大增加,最终得出多齿铣削力预测模型公式为:
F=F(φ)+F′(φ)
(28)
得出F1的平均偏差为11.05%,F2的平均偏差为10.49%,F3的平均偏差为11.67%。
引入一组新刀具位置角φ′(从0.5开始间隔0.5取值至6结束)用以检验该模型的预测效果,经过仿真计算得知,F1的平均偏差为13.53%,F2的平均偏差为11.21%,F3的平均偏差为11.5%,其数据对比情况如表3所示,对比图如图7所示。

表3 实验数据与仿真数据对比
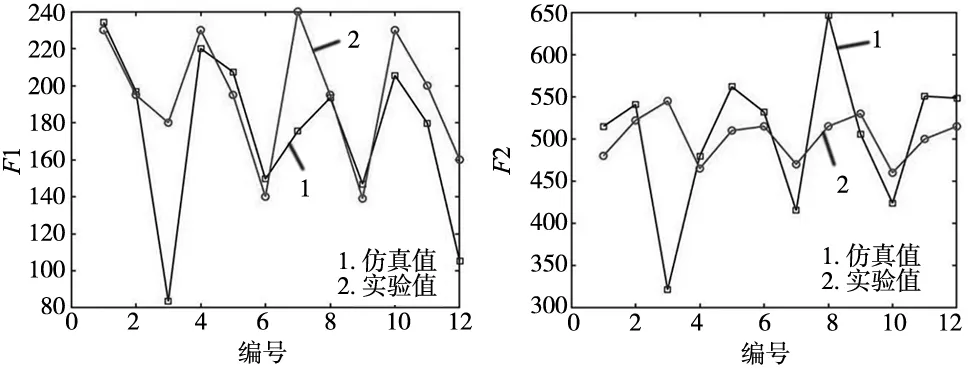
(a) 测试后F1对比图 (b) 测试后F2对比图

(c) 测试后F3对比图
4 误差分析
通过对比文献[22]中的传统多齿铣削力预测情况可知,shannon改进的预测模型在个别节点处的预测效果不理想。究其原因,为实验采样时的采样误差,以及采样节点数量所致。
由于该方形槽应用于传动机构中,且该传动机构材料为45钢,由应力公式得:
(29)
式中,ΔFmax为铣削力最大误差值(理论值和实验值之差);δ为表面应力;S为工件面积;δs为45钢屈服极限。
由式(29)可得,ΔFmax不会使工件产生变形,即不影响加工后传动机构的传动精度。
综上所述,当采样质量提高时,该模型预测误差率可以降至10%以下,即预测误差符合精度要求。
5 结论
多齿铣削力的预测模型是一个热门且亟待解决的课题,通过上述证明,仿真及实验可知:
(1)shannon定理可以对多齿铣削力模型进行一定程度的改进,但需要引入修正信号;
(2)遗传算法能够完成对铣削力模型参数的寻优,且改进后的多齿铣削力模型可以预测铣削力,并且能够将模型预测误差率降至10%以下;
(3)经改进后的铣削力模型,可更为便利地应用于智能加工仿真系统中。为智能系统后续的改进及优化提供理论依据。

