先进复合材料液体成型工艺多尺度树脂流动数值模拟研究

李 晨，秦晓陈，陈 程，高丽敏，徐吉峰，2

（1. 中国商飞北京民用飞机技术研究中心民用飞机结构与复合材料北京市重点实验室，北京 102211；2. 太原理工大学，太原 030024）

相较于传统结构材料，先进复合材料因具有较高的比模量、比强度，抗疲劳性能和耐腐蚀性好，便于一体化成型等诸多优点，被广泛应用于航空航天、交通设备制造等领域[1]。当前，复合材料在民机结构上的应用比例在一定程度上已成为衡量民机先进性的重要指标。民用航空领域对复合材料的经济性和安全性提出了更高要求，复合材料制品的成本主要源于原材料和成型工艺两部分，其中制造方面的成本通常约占到总成本的70%[2]。

在诸多制造工艺中，复合材料热压罐成型是目前应用最广泛、用量最大的复合材料与结构制备技术。作为一种具有代表性的先进复合材料低成本制造技术，复合材料液体成型（Liquid composites molding，LCM）工艺可以避免使用造价高昂的热压罐设备，而选择使用成本较低的烘箱或者固化炉等，同时该工艺具有制件表面质量好、精度高、制造效率高等诸多优点而得到广泛关注。如俄罗斯MC–21客机和空中客车公司A220系列飞机等都已经将自动铺丝液体成型技术用于飞机重要承力结构的制造中[3]。真空辅助树脂转移成型 （Vacuum assisted resin transfer molding，VARTM）工艺作为液体成型工艺中较常见的方法，近年来也已被广泛应用于复合材料制件成型。典型的VARTM工艺树脂流动浸渍的过程如图1所示[4]。树脂浸渍过程是该方法制备复合材料是否产生缺陷的关键环节。

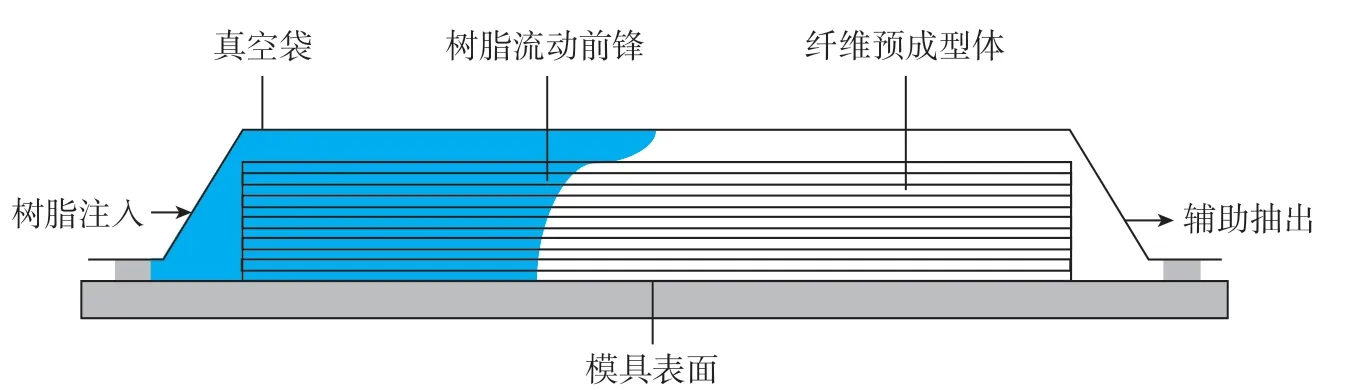
图1 VARTM工艺树脂浸渍过程示意图[4]Fig.1 Sketch of VARTM during resin infusion process[4]

传统上采用液体成型工艺进行复合材料件制备和工艺优化前，往往需要依靠经验设计树脂注口位置并通过大量试验试制对树脂浸渍情况进行判定，不仅影响研制周期，还会带来极大的试制成本。采用数值模拟对模具内树脂流动情况进行工艺仿真分析可以有效降低工艺设计成本，有利于优化工艺参数，并提高制造效率。国外许多学者开发了LIMS程序，从试验和仿真方面对液体成型工艺进行了较为系统的研究[5–8]。国内学者也针对液体成型工艺仿真开展了广泛研究[9–11]。戴福洪等[12]采用控制体积法模拟边缘效应，然而控制体积法计算精度较低，一定程度上影响了预报结果。Li等[13–14]采用有限元方法和相场法对树脂在微观和细观层面的流动进行了研究。目前，国内外对液体成型树脂流动的数值模拟研究主要集中在宏观尺度，然而工艺缺陷等往往是微观和介观尺度问题在宏观层面的集中表现。本文通过有限元方法，基于Comsol Multiphysics多物理场仿真软件研究了纤维预成型体从微观到介观尺度的渗透率，在宏观尺度上采用理查德方程作为流动控制方程，实现了对充模过程树脂瞬时流动前锋和流场压强进行预报，并在各个尺度层级上与现有理论或试验进行了对比，验证本文方法的正确性。

1 复合材料预成型体多尺度结构与渗透率

通常，纤维单丝 （μm级别）层面被认为是不可被渗透的最小尺度，即微观尺度；而纤维束内和束间 （μm～mm级别）介于微观和宏观制件尺度间则被称为介观或细观。图2展示了典型的纤维单丝微观尺度、纤维束内和束间介观尺度及宏观尺度形貌特征，其中纤维束外轮廓一般呈椭圆形结构。

在微观尺度上，纤维单丝间的随机排布形成树脂流道，符合层流自由流的特征；而在介观层面，当纤维束被看作一个整体时，该区域符合多孔介质渗流特点，纤维束外仍是层流自由流；在宏观尺度上，则可从整体上认为是一个多孔介质渗流区域。

渗透率是衡量多孔介质结构允许树脂流动渗透能量的表征量，是材料固有属性，与所渗透的液体和外施条件无关，渗透率也是数值模拟中重要的参数。渗透率常用K表示，其定义由Darcy定理引出，即

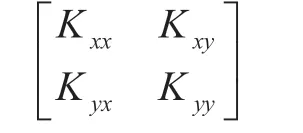
三维渗透率张量可表示为

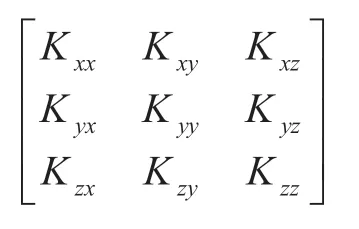
宏观尺度由微观和介观经过尺度升级获得，逐级将渗透率数据代入代表性单胞结构有限元模型中，多尺度的几何结构模型成为整个多尺度树脂流动数值模拟研究的基础和载体，而多尺度的渗透率则成为连接不同尺度进行数值模拟尺度升级的主线，不同尺度渗透率之间的联系如图3所示。

图3 不同尺度渗透率的联系Fig.3 Relationship of multi-scale permeability

2 基于有限元方法的多尺度树脂流动数值模拟研究流程

本文从微观尺度结构建模和渗透率预报研究入手，进而扩展到介观尺度并逐级对研究尺度进行升级，最后得到宏观尺度渗透率，并基于此开展全局树脂流动数值模拟研究与试验结果进行比对。整个研究流程如图4所示。

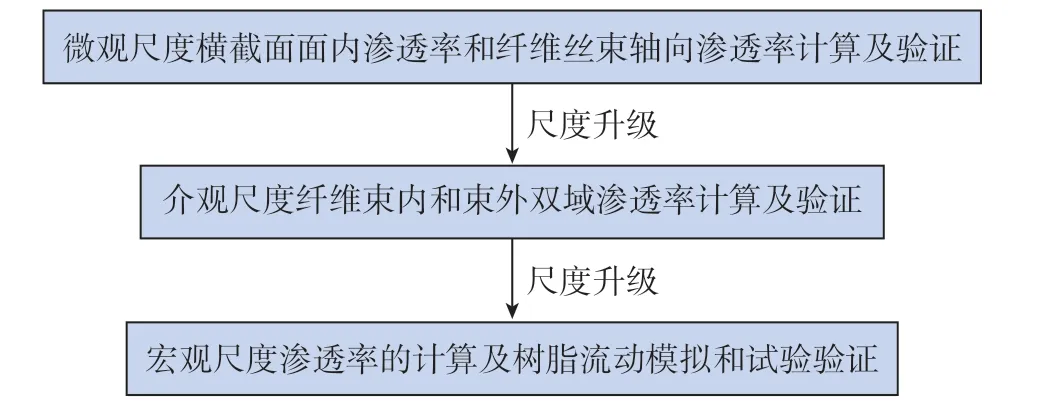
图4 多尺度树脂流动数值模拟研究流程Fig.4 Flowchart of numerical simulation of resin flow at multi-scale

对树脂浸渍流动进行数值模拟可以归属为计算流体力学的研究范畴，控制方程是数值模拟计算过程的核心，是对物理过程的公式化表述；有限元法则通过对计算域进行网格划分、控制方程和初始条件的离散，进行求解以达到迭代计算的结果满足收敛误差条件。

3 多尺度树脂流动数值模拟理论

本文为满足控制方程的使用条件，进行如下假设：

（1）认为纤维预成型体为符合多孔介质定义的连续结构，且在树脂流动浸渍过程中对结构的形变影响忽略不计；

（2）树脂在纤维预成型体中的流动为多孔介质渗流并满足达西流体流动特性；

（3）温度恒定且树脂流动不受温度变化影响，即树脂流动时黏度保持一定，且不考虑树脂流动时的相变和物理化学反应等。

3.1 微观尺度树脂流动理论

Navier–Stokes方程是描述黏性不可压缩流体动量守恒运动的经典方程，通过求解式（2）和质量守恒方程，即连续性方程（式 （3）），可以得到速度场u，代入Darcy定理计算得到渗透率。

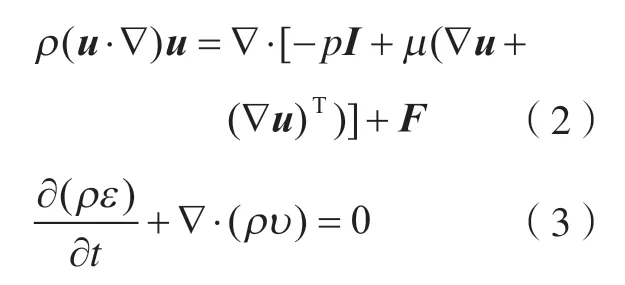
式中，ρ为树脂的密度；u为流动速度；p为压强；μ为动态黏度；F为体积力；I为单位向量；ε为纤维预成型体的孔隙率。在稳态流动下，流体不可被压缩，ρ为常数，式 （3）可化简为式（4），即

式中，v为速度向量。

3.2 介观尺度层流和渗流耦合流动方法研究

纤维束内部是由纤维单丝和它们之间的间隙构成的多孔介质结构。树脂流动穿过多孔介质结构为多孔介质流动，树脂在纤维束之间的空隙流动为自由流。当忽略惯性项时，方程变为Stokes方程。由于雷诺数远小于1，且认为流体不可压缩，自由流变为蠕动流，并且在多孔介质外部和内部的流动是连续的。两种流动在微观尺度上可以用统一的控制方程Brinkman公式来描述。Brinkman公式在Stokes方程基础上引入Darcy项，拓展了应用范围，所形成的Stokes–Brinkman方程恰当地描述了层流和渗流的耦合流动，即

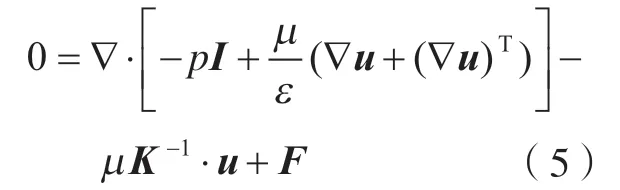
在多孔介质中，Darcy项“μK–1·u”起着关键作用，而在自由流域中，由于ε= 1，K趋于无穷大，Darcy项消失，方程可简化为Stokes方程。

3.3 宏观尺度树脂流动模拟

宏观尺度控制方程采用多孔介质渗流理查德方程，即

式（7）为树脂流动轮廓方程，建立了树脂流动饱和度S和压强p之间的关系，直观反映了宏观尺度上树脂流动前锋的位置并与实际树脂浸渍自动干丝铺放的预成型体试验及理论解析解进行对比验证，能够对树脂流量、用量和树脂充模完成时间进行预报。

4 多尺度有限元建模及验证

4.1 微观尺度渗透率计算及验证

根据采集的微观尺度纤维束内结构形貌，基于Monte Carlo随机算法建立纤维束内正方形区域几何模型 （孔隙率ε= 0.5，纤维单丝直径rf= 0.0035 mm，纤维数量n= 122）。对于渗透率计算的稳态数值模拟，本文采用P1–P1进行有限元离散化，用线性单元P1对速度u和压力p进行离散化，网格划分情况和速度场如图5所示。

图5 纤维束内正方形区域网格划分与速度场分布Fig.5 Fibers intra square domain meshing and velocity distribution

由图6可知，基于Monte Carlo随机排布结构计算的渗透率值低于Kozeny–Carman方程和Gebart方程[15]等经验公式，但与其他采用随机建模方法学者计算值接近。这是由于规则排布的纤维间容易形成较通畅的“流道”，而随机排布的结构纤维相互交错容易造成“流道”的堵塞，进而导致流体难以渗透通过，并直观表现为渗透率值的下降[16–17]。

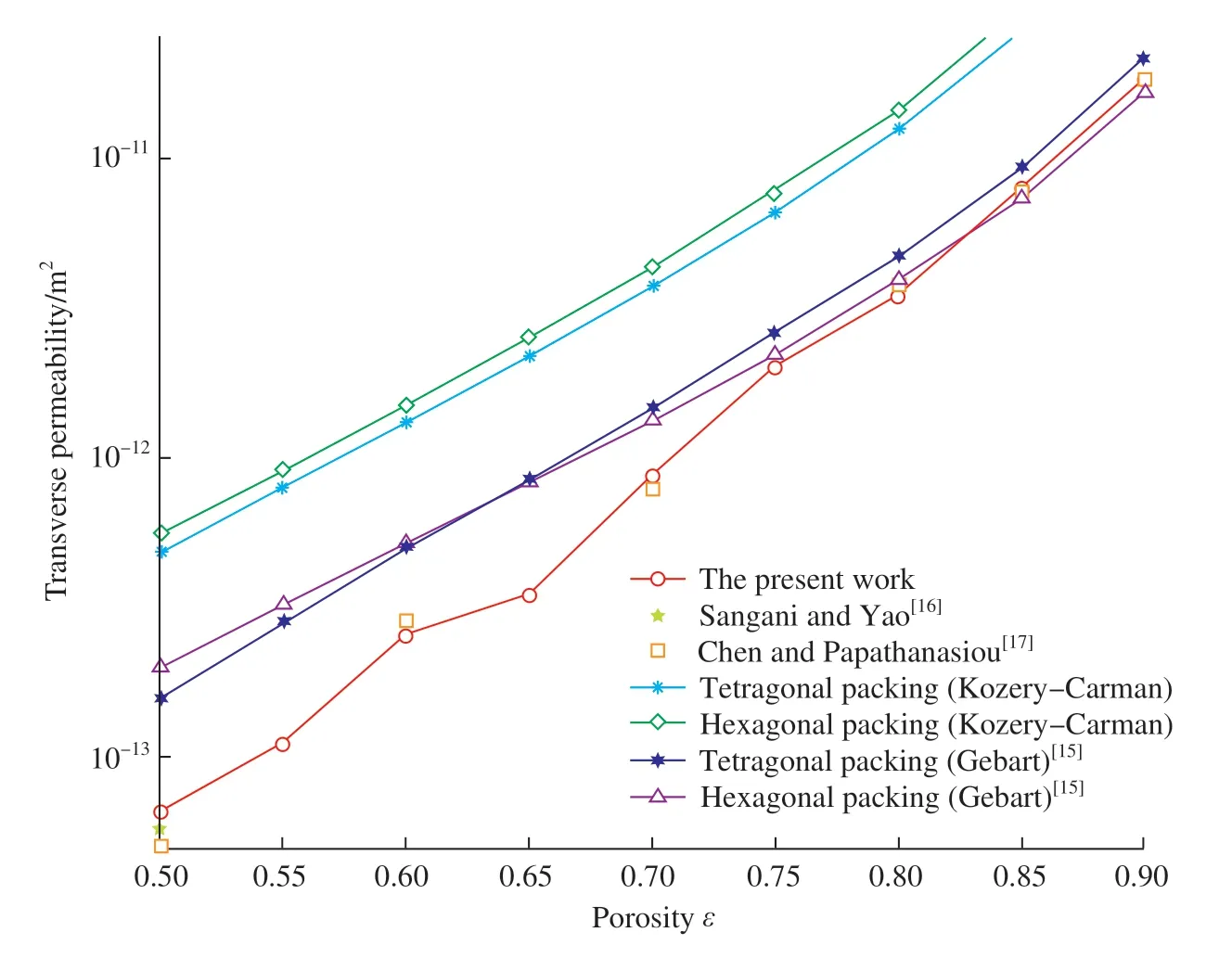
图6 随机排布与经验公式渗透率结果对比Fig.6 Comparison of permeability results between random configuration and empirical formula

4.2 介观尺度渗透率计算和验证

本文基于平纹玻璃纤维编织结构，采用TexGen软件建立介观尺度纤维束内和束外单胞结构，如图7所示，前后两侧分别为入口和出口条件，其他4个面为周期性边界条件。

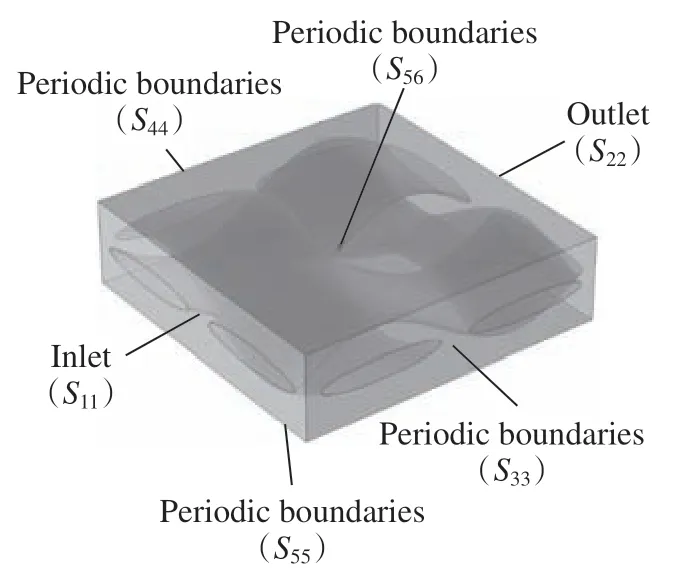
图7 介观尺度可重复单胞结构Fig.7 Repeatable unit cell structure at mesoscale

将微观尺度计算获得的渗透率数值代入纤维束区域，计算纤维束内与束间单胞结构的渗透率，所得的速度流场如图8所示。

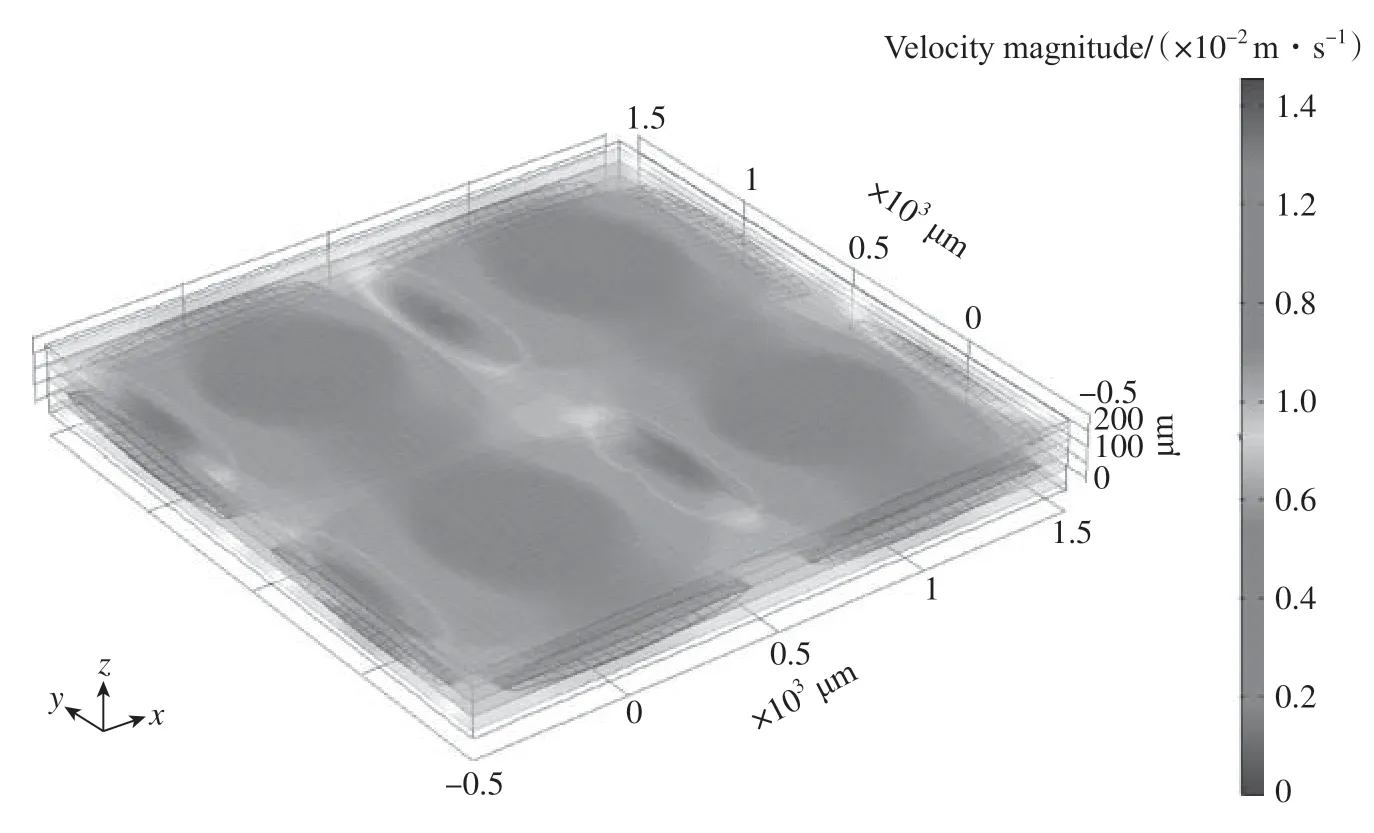
图8 单胞结构速度场Fig.8 Velocity field of unit cell

将基于本文模型方法的计算结果与文献[18–19]改进的单胞渗透率计算值相比，误差在5%以内，如表1所示。

表1 渗透率对比[18–19]Table 1 Comparison of permeability[18–19]

4.3 宏观尺度数值模拟与试验验证

（1）试验设计和有限元建模。为验证本文方法的正确性，本文将宏观尺度与树脂浸渍试验 （图9）进行对比，试验设备由树脂注射系统和位于树脂注射系统上方的监测系统两部分构成，其中监测系统负责记录试验中不同时刻树脂流动前锋位置。本文采用Textile Aero Tarn公司生产的平纹编织玻璃纤维材料作为预成型体进行单层铺放，外覆真空袋。

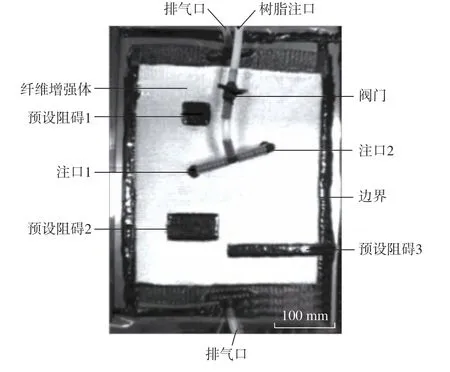
图9 树脂流动浸渍试验设计Fig.9 Experiment design of resin flow and infusion

在纤维预成型体上预设了两个镂空区域，在临近下端的位置预设阻碍区域与整个矩形边缘区域相联通，忽略厚度方向树脂浸渍影响，采用二维平面模型模拟树脂流动。运用三角形单元对几何模型进行有限元划分后的结果如图10所示，采用三角形网格，共划分为5760个域单元。

图10中除了两个位于几何模型中部的圆形树脂注入口，其他边界条件均设为不可渗透。初始状态模具内压强与出口压强差为0；树脂注入初始阶段，入口压强 （Pin）和出口压强 （Pout）压差为0.1 MPa，试验和数值模拟选用的树脂黏度和纤维预成型体的渗透率值沿竖直方向K1和水平方向K2由前述章节中方法计算获得。具体参数如表2所示。

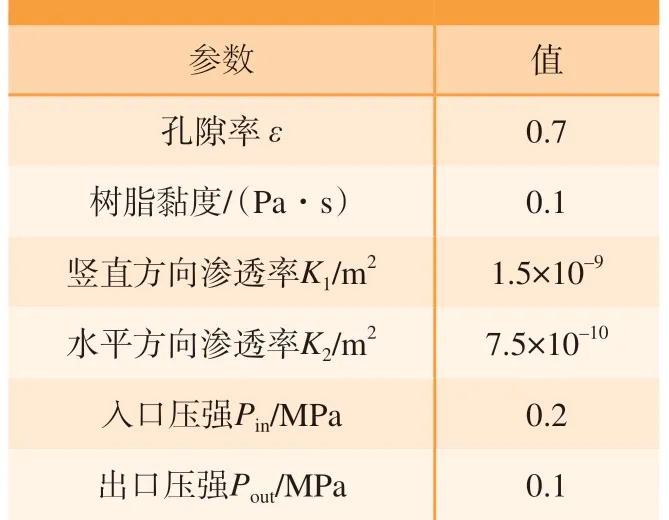
表2 材料参数Table 2 Material property

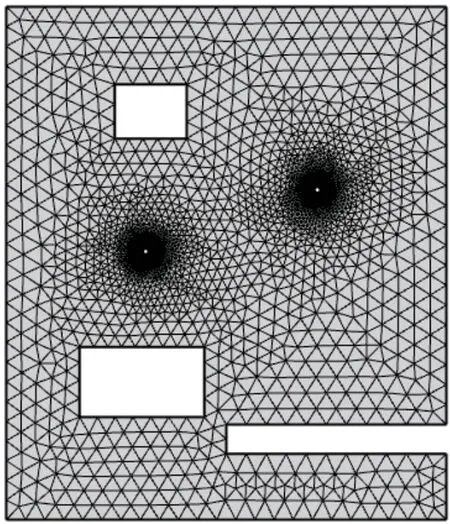
图10 网格划分Fig.10 Meshing

（2）结果对比验证。不同时刻的树脂流动前锋位置和压力场的试验结果和数值模拟结果如图11所示。其中，图11（a）和（e）为不同时刻试验所得树脂流动前锋的记录。图11（c）和（g）为Gantois等[20]采用边界元法得到的压强场云图。图11（b）和（f）、图11（d）和（h）分别为本文所采用方法获得树脂流动前锋和压强场的结果。

图11 不同时刻的树脂流动前锋位置和压力场的试验结果和数值模拟结果对比Fig.11 Comparison of experimental results and numerical simulation results of resin flow front position and pressure field at different time

为量化试验与数值模拟对比结果，本文提出了浸润比的定义，即λ=S树脂/S纤维，其中S树脂代表瞬时投影面内被树脂流动浸渍区域面积；S纤维代表整个纤维预成型体铺放区域面积。对比不同时刻数值模拟结果与试验结果的浸润比λ绝对值差|λ试验–λ模拟|均小于10%；同时，将不同时刻压强场结果与Gantois等[20]结果进行了对比，亦得到近似结果，证明了本文方法具有良好的预报准确性。

5 结论

本文研究了从纤维束内部微观尺度到纤维束内和束间介观尺度渗透率预报方法，并进行对比验证；基于微观和介观尺度渗透率进行尺度升级，在宏观尺度实现了对树脂浸渍纤维预成型体过程瞬时流动前锋的数值模拟预测并通过提出浸润比的概念对树脂浸润情况进行量化与试验结果对比。本文初步建立了一套较为完整的跨越微观、介观和宏观多尺度域集预成型体渗透率预报与树脂渗流的数值模拟方法体系。

在后续数值模拟研究工作中，可以考虑温度变化对流体流动特性的影响（如树脂黏度的影响）。本文所建立的方法，目前仅对较为简单的复合材料结构的树脂流动仿真进行了验证，在后续研究中可以继续将该方法扩展到更复杂结构模型中进行探讨研究。