基于向量场法的固定翼无人机制导算法的设计与实现

周晨昶，王道波，王 猛

(南京航空航天大学自动化学院，江苏 南京 211106)

0 引言

无人机大致分为消费级与工业级2类[1]，前者主要用于个人娱乐、拍照创作等，后者可进行地形勘探、搜索救援以及多种军事用途等。无人机之所以能在众多领域发挥作用，较为重要的一点在于它能够较为精确地跟踪预设航线飞行[2]。同样，无人机在飞行前，地面站会向飞控系统设定预设的航线，无人机在空中能自主跟随预设的航线路径，完成飞行任务。

针对路径跟随这项技术，国内外的学者做了很多研究。依据解决策略的不同，大致分为2类。一类被称为几何学方法，如追踪法[3]、视线法[4-6]，以及本文将重点介绍的向量场法[7-9]。追踪法要求无人机的速度矢量始终指向目标方向，视线法则设置虚拟点，逐步将无人机引导至路径上，这些技术主要用于导弹制导方向。Kothari等[10]曾将追踪法与视线法相结合，提出了PLOS(pure pursuit and line-of-sight)算法，使得无人机可以更好地在有风环境下实现路径跟随。Park等[11]提出一种基于虚拟目标点的非线性制导律，使得无人机在飞行过程中逐步收敛至目标路径。也有学者将几何学方法与智能算法相结合，如Tabatabaei等[12]将Carrot-chasing算法与遗传算法和模糊控制相结合，提出了三维模糊Carrot-chasing(3D fuzzy Carrot-chasing)算法，使得无人机在风干扰环境下拥有更好的路径跟随结果。另一类被称为控制学方法，分为线性控制技术与非线性控制技术，主要以非线性控制技术为主。工程应用中较为常见的便是PID控制技术。Rhee等[13]对传统PID技术进行改进，加入前馈环节，大大提高了无人机的路径跟随性能。主要的一些非线性控制技术包括线性二次型调节器(LQR)[14-15]、滑模控制[16]、模型预测控制[17]、自适应控制[18]等。Wu等[19]在风扰动环境下，将无人机的飞行控制系统简化为4个回路，并对每个回路设计不同的非线性控制器，以实现三维空间内的路径跟随问题。基于非线性控制理论的路径跟随技术往往具有更好的鲁棒性，使无人机具有更好的飞行稳定性。但此类方法较为依赖数学模型，实际应用相对复杂。

针对众多的路径跟随算法，许多学者进行了结合或比较。Xue等[20]将Carrot-chase与PLOS这2类算法进行比较，发现只要选择合适的制导律增益，两者均能较好地实现路径跟随。Sujit等[21-22]将5种不同策略的路径跟随算法进行比较，加入风场扰动，并通过蒙特卡罗模拟，最终发现向量场法有着更好的抗风干扰能力，能够更为有效地实现路径跟随。

路径跟随算法的选择往往要在控制精度与计算工作量之间进行权衡。本文为提高某中小型固定翼无人机在有风环境下的控制精度，优化路径跟随性能，设计了一种基于向量场的侧向制导算法，代替了基于PID的侧向制导算法。最终通过数字仿真实验，证明了向量场制导算法的优越性，通过半物理仿真以及实际飞行，验证了该算法与PID纵向制导算法融合后，可控制该固定翼无人机在有风干扰的环境下更好地实现路径跟随。

1 问题描述

首先给出本文所考虑的无人机数学模型，然后给出路径跟随问题的数学模型。飞行路径主要由直线段和圆弧段构成，本文主要考虑直线段与圆弧段的路径跟随问题。

1.1 无人机数学模型

无人机的横向与纵向控制系统包含3个闭环回路[23]，在设计时，增稳回路和姿态回路的传递函数增益近似为1，横向和纵向控制回路的简化框图分别如图1和图2所示。

图1 横向运动控制回路简图

图2 纵向运动控制回路简图

动力学方程即可表示为：

(1)

(2)

滚转角指令以及俯仰角指令可表示为：

(3)

(4)

实际飞行中，航线角指令χc往往会实时变化，而高度指令hc往往以固定值的形式由预设航线给定或者由地面站发出，纵向自动驾驶仪将自主控制无人机跟随指令高度飞行。因此，接下来主要讨论直线段与圆弧段路径的侧向跟随问题。

1.2 路径跟随

直线段路径侧向跟随俯视图如图3所示。

图3中，O为路径起点，χq为目标路径的航线角，ePx和ePy为无人机与目标路径的航迹误差分量，通过坐标转换可表示为

图3 直线段路径跟随俯视图

(5)

定义1：当ePy近似为0且数值稳定时，无人机便完成了直线段路径侧向跟随，且ePx数值越小，无人机的侧向制导效果越好。

圆弧段路径侧向跟随俯视图如图4所示，其中d为无人机与圆弧中心点的距离向量；φ为其对应的相位角；向量m与圆弧相切，其方向角为χo。

图4 圆弧段路径跟随俯视图

经过坐标转换，得到无人机在d方向与m方向上的运动情况为

(6)

即：

(7)

(8)

定义2：当‖d‖近似等于ρ且数值稳定时，无人机便完成了圆弧段路径侧向跟随。

加入风扰动后，无人机的地速矢量Vg，空速矢量Va和风矢量W的关系如图5所示。在xy平面讨论无人机侧向制导问题时，运动学方程可表示为：

图5 无人机地速、风速和空速矢量关系

(9)

(10)

2 无人机路径跟随算法设计

2.1 PID制导算法

该无人机的俯仰指令公式[24]和滚转指令公式[25]为：

(11)

(12)

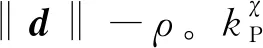
2.2 向量场侧向制导算法设计

PID侧向制导算法实时计算出无人机飞行过程中所需的滚转指令，现基于向量场的思想，设计一种利用侧偏距，实时计算出航线角指令输入χc的侧向制导算法 。

该算法只考虑侧偏距作为影响航线角指令变化的唯一因素，因此即使当风等外部干扰存在时，只要当无人机的侧偏距存在，横向姿态控制回路便会收到相应的航线角指令，以控制无人机消除侧偏距，完成侧向制导。

2.2.1 直线段路径侧向制导

无人机进行直线段路径侧向跟随时，当前位置的期望航线角即可作为侧向制导所需的航线角指令χc。这些期望航线角可以理解为具有指向功能的向量，构成了侧向制导所需的向量场，如图6所示。

图6 基于向量场法的直线段路径侧向制导策略

图6中，χ∞表示当无人机远离路径时的期望航线角，此时无人机几乎径直飞向路径。当无人机位于路径右侧时，χ∞=χq-π/2；当无人机位于路径左侧时，χ∞=χq+π/2。当ePy=0时，χc=χq。

定理1：假设无人机以恒定的速度飞行，目标直线段路径方向已知，为完成侧向路径跟随，无人机在当前位置下的期望航线角可表示为

χc(ePy)=-arctankmePy+χq

(13)

km为常值系数。km的取值影响了反正切函数值的变化速率，进而影响了期望航线角从χ∞到χq的转换速率。

当|χq-χ|>π时，此时给出的航线角指令往往要求无人机调整的航线角度超过180°，如图7所示。

图7 靶机的航线角与指定航线角相差较大

此时，χc>0。无人机航向控制回路会严格跟踪航线角指令，此时无人机完成侧向制导所需调整的角度为χ+χq；如果χq可用略小于-π的角度进行表示，则χc<-π，无人机便会向左调整航向，更利于飞行。那么，此时目标路径的航线角χq可表示为

(14)

n∈N,其取值使得|χc-χ|<π；单位向量q=(qnqe)T指向路径方向，qn、qe分别为北向和东向的分量。完成航向调整后，再将当前航向χ与航线角指令χc调整至区间[-π,π]内。

2.2.2 圆弧段路径侧向制导

与直线段路径侧向制导原理相同，无人机圆弧段路径侧向制导策略如图8所示。

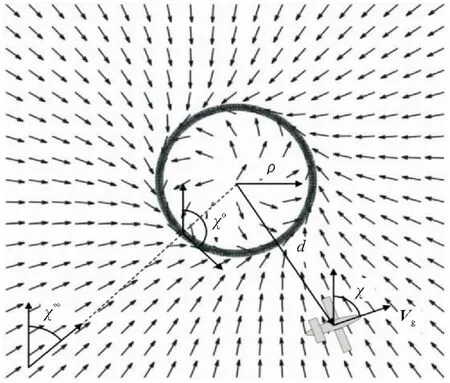
图8 基于向量场法的圆弧段侧向制导策略

图8中，χo为无人机在圆弧段路径上飞行时的期望航线角，可表示为

(15)

χ∞为当无人机远离圆弧段路径时的期望航线角，此时无人机几乎径直飞向圆弧中心，表示为

(16)

其中，当无人机准备以顺时针方向驶入轨道时，λ=1；当无人机准备以逆时针方向驶入轨道时，λ=-1。

定理2：假设无人机以恒定的速度飞行，目标圆弧段路径位置已知，为完成圆弧段侧向路径跟随，无人机在当前位置下的期望航线角可表示为

(17)

kn为常值系数。kn的取值同样影响了输入的航线角指令的过渡速率。侧向跟随过程中，无人机在逐渐贴近圆弧段路径飞行时，航向变化最大。若kn取值过大，航线角指令变化较为急促，不利于飞行；若kn取值过小，航线角指令变化不及时，难以满足路径跟随要求。

同样在实际的应用中，无人机在进行圆弧段侧向路径跟随时，部分位置会发生航线角指令的突变，以图9为例。

在图9a中，无人机的当前航线角大小为π，由于航线角的变化区间为[-π,π]，当无人机经过该位置时，航线角指令χc≈-π，受控的航向会发生2π的突变；图9b中，无人机经过该位置时，相位角φ同样会发生幅值为2π的突变，从而造成航线角指令的变化。因此，当|χc-χ|>π时，需对无人机相位角进行修改，即

图9 航线角指令发生2π突变

φ=arctan(pe-ce,pn-cn)+2πn

(18)

n∈N，n的取值使得|χc-χ|<π，航线角指令便不会发生幅值为2π的突变。

3 仿真实验与实际飞行

首先通过数字仿真实验，将基于向量场的侧向制导算法与PID侧向制导算法进行对比，以证明前者的优越性；然后采用改进制导算法对固定翼无人机进行了半物理仿真试验，以证明算法有效性。

3.1 数字仿真实验

仿真实验包括3部分，分别为近距离直线段路径侧向跟随、远距离直线段路径侧向跟随和圆弧段路径侧向跟随。假设无人机的初始航向为90°，飞行速度为20 m/s。运算步长为0.01 s。

3.1.1 近距离直线段路径侧向跟随

目标路径y=0，无人机的初始位置为(0,100)，风速为6 m/s，方位角为315°。2种控制算法的仿真结果如图10～图13所示。图10为近距离直线段路径的侧向跟随结果，图11、图12和图13分别为无人机侧偏距、航线角和滚转角的变化曲线。

图10 近距离直线段路径跟随结果

图11 侧偏距变化

图12 航线角变化

图13 滚转角变化

采用向量场法时，无人机在30 s左右完成侧向制导，跟随误差2.1 m；采用PID制导算法时， 无人机54 s后跟踪误差收敛至2.1 m内，但航向并不稳定。

上述结果可以看出，向量场制导算法控制下的无人机收敛至目标航线的时间更短，航向控制更为精准，跟随误差更小，同时滚转角振荡较少，飞行更平稳。

3.1.2 远距离直线段路径侧向跟随

目标路径y=0，无人机的初始位置为(0,400)，风速为6 m/s，方位角为315°。2种控制算法的仿真结果如图14～图17所示。

图14 远距离直线段路径跟随结果

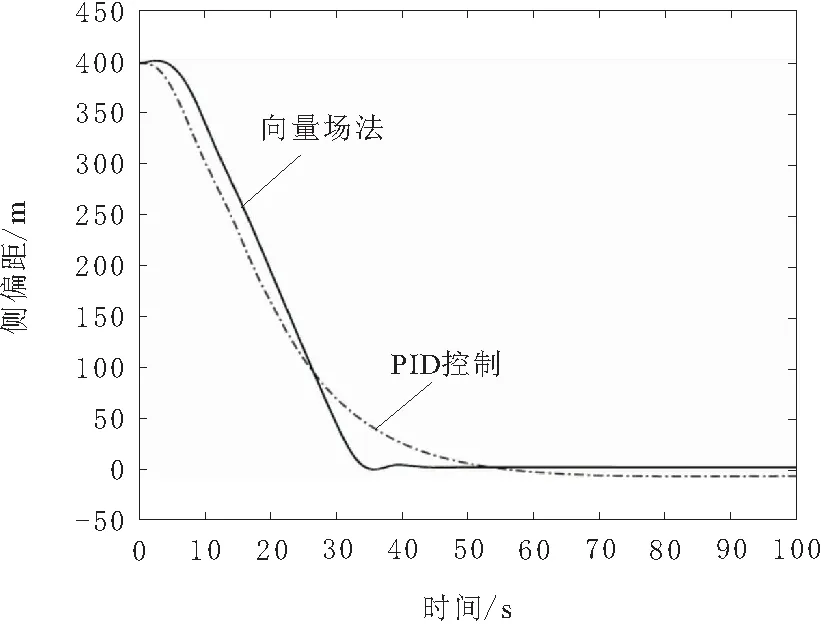
图15 侧偏距变化

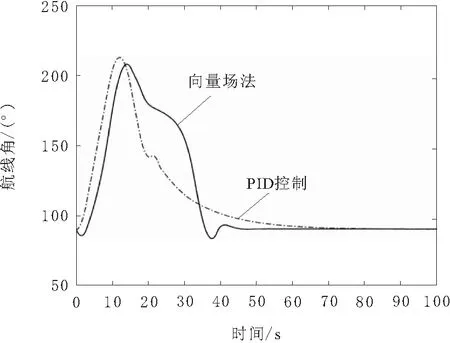
图16 航线角变化

图17 滚转角变化

采用向量场法时，无人机46 s后实现航向稳定，完成侧向制导，跟随误差约3.5 m；采用PID制导算法时，无人机77 s后完成侧向制导，跟随误差约为5.5 m。

当无人机距离目标航线更远，向量场制导算法的优势更加明显。向量场制导算法控制无人机收敛至目标航线的调节距离明显更短，飞行曲线更为平滑，跟随误差更小，制导效果明显更优。

3.1.3 圆弧段路径侧向跟随

期望圆弧段路径由2个半径为200 m的半圆弧组成，无人机初始位置为(0,200)，风速为6 m/s，方位角为315°。2种控制算法的仿真结果如图18～图21所示。

图18 圆弧段路径跟随结果

2种算法控制下的无人机在前半段路径中的跟随效果相仿，但在后半段路径中，采用PID制导算法时，无人机出现较大的震荡与超调，随后逐渐收敛。从图20和图21中可以看出，向量场制导算法控制无人机74 s完成圆弧段的飞行任务，而PID制导算法控制无人机81 s完成圆弧段的飞行任务。

图20 航线角变化情况

图21 滚转角变化情况

总体而言，在圆弧段路径侧向跟随任务中，向量场制导算法控制下的无人机飞行耗时更短，跟随误差更小，飞行过程更加平稳，制导效果更好。

图19 侧偏距变化情况

3.2 半物理仿真实验

搭建仿真平台，开发环境选用Microsoft Visual C++ 6.0。依据该无人机具体参数，结合6个动力学方程和6个运动学方程构造其数学模型。无人机起飞方式为弹射起飞，仿真平台中包含了火箭助推器模型以及发动机模型[26]，以模拟无人机的真实飞行。同时，加入水平方向上的常值风，模拟风的干扰。

选择向量场法为侧向路径跟随算法。模拟起飞前，上传预定航线至飞控系统，输入无人机起飞点的经纬度以及起飞时的航线角和俯仰角，输入干扰风的方位和风速。模拟起飞后，仿真平台接收飞控传入的舵面信息并经过解算，将取代GPS以及陀螺仪，发送经纬高、航线角、三向加速度以及欧拉角等数据给无人机的飞控系统。飞控接收后进行解算，同时控制舵面偏转，完成路径跟随，并将所有数据由无线电台发送至地面站，地面站可观测飞行期间所有状态数据，且全程可控。半物理仿真流程如图22所示。

图22 仿真流程

输入无人机起飞时仰角大小为15°。风的方位角设为45°，风速大小为6 m/s。仿真结果如图23和图24所示。

图23 侧向路径跟随

图24 纵向高度跟随

图23中，坐标(0,500)为起飞点，无人机在第二圈飞行不久后进行回收。飞行曲线平滑，无明显抖动与振荡，无人机与直线段路径和圆弧段路径贴合度较高，高度跟随过程较为平稳，路径跟随情况良好。向量场侧向制导算法与纵向制导算法融合效果较好，验证了向量场侧向制导算法的有效性。

4 结束语

为提高某中小型固定翼无人机在有风环境下的路径跟随性能，本文设计了一种基于向量场的侧向制导算法。该算法通过提供实时精准的航线角指令，控制无人机迅速调整姿态，修正航向。数字仿真实验表明，在有风的环境下，与原PID侧向制导算法相比，该算法控制无人机收敛至目标航线的调节时间更短，调节距离更短，航向控制更加精准，跟随误差更小，飞行过程更加平稳，制导效果明显更优。最终，半实物仿真实验证明了向量场侧向制导算法与PID纵向制导算法可较好融合，算法改进后的无人机拥有更好的抗风干扰能力，路径跟随性能明显增强。