单层悬索光伏支架静力分析及简化计算方法

杨政， 贺拥军*， 全勇

(1.湖南大学土木工程学院， 长沙 410082； 2. 中机国际工程设计研究院有限责任公司， 长沙 410021)

由于传统石油资源的持续消耗，国际能源危机和环境问题不断恶化[1-2]。太阳能作为最受欢迎的可再生能源之一，因其具有清洁、安全、取之不尽用之不竭的优势，日益受到人们的重视[3]。因此，世界各地均在建设大量的光伏项目以满足快速增长的能源需求。

然而，传统的光伏支架对土地的要求较高，且无法进行土地的二次利用。为此，Baumgartner等[4]研发了拉索支承光伏支架，该支架采用施加预张力的拉索代替传统的梁-檩条体系来固定和支撑光伏板，并将荷载传递至两侧的下部支架及基础。同时，其具有跨度大、质量轻、用钢量少、能适应复杂地形等优点。

目前，拉索支承柔性光伏支架尚属起步阶段，以往研究主要集中在拉索受力、下部支架角度等方面，王雨[5]介绍了柔性光伏支架的两种基础形式和组件排布形式，考虑温度对预应力索的影响，提出较优的索张拉工序；唐俊福等[6]对比了3种不同形式的下部支撑构件，并研究其与地面倾角的变化对结构受力特性的影响，给出了不同地质情况和安装角度的下部水平承载构件的推荐；周杰等[7]对山区柔性光伏支架进行分析，采用2.0作为拉索的抗拉设计分项系数，跨度的1/15作为挠度控制值，并给出了主索和稳定索的预张力计算范围；另外，牛斌[8]研究了单层和双层悬索结构的基本受力特点，分析两者的不足之处，并提出刚性支架与柔性索桁架相组合的设计方案和张拉办法。

然而，在进行单层悬索光伏支架的静力分析时，由于拉索的预张力导致梁端节点所受水平力较大，且位移影响不能忽略[9]，但鲜有研究拉索在边梁支座位移下的受力情况；并且，大多数研究将光伏组件等效为线荷载，没有考虑光伏组件对拉索的作用，从而忽略了光伏组件的受荷状况。因此，现对单层悬索光伏支架进行整体结构分析，考虑到光伏组件对拉索的拉结作用，研究单层悬索光伏支架各构件的受力性能以及光伏组件的内部应力；而后，根据单层悬索光伏支架的受力特性以及结构特征，建立简化计算模型，提出一种考虑支座位移的单索线形简化计算方法，以期为后续的单层悬索柔性光伏支架设计提供参考。

1 有限元模型的建立与验证

1.1 结构构成

单层悬索柔性光伏支架下部支承构件主要由基础、边梁、边柱、拉杆、中间梁柱钢架以及拉索组成。拉索呈上下分布用以支撑光伏组件。取两榀五跨单层悬索光伏支架为研究对象，结构总长度75 m，下部支架间距L为15 m，边柱间距l为6 m，柱高4 m，结构示意图如图1所示。

图1 单层悬索光伏支架结构示意图Fig.1 The structure of single-layer cable-suspended photovoltaic support

1.2 模型的建立

拉索采用Φ12.7 mm的热镀锌钢绞线。边柱、边梁与中梁均为焊接组合H型钢，截面尺寸分别为：250 mm×160 mm×6 mm×10 mm、400 mm×280 mm×8 mm×12 mm与300 mm×200 mm×8 mm×12 mm；柱间支撑、外侧拉杆与中柱分别采用尺寸为Φ70 mm×5 mm、Φ120 mm×8 mm与Φ160 mm×8 mm的空心圆钢管。钢材均选用Q345B。拉索及光伏组件材料属性如表1所示。

采用SAP2000对整体结构进行建模：拉索采用cable单元模拟；光伏组件采用shell单元模拟并选用等效厚度的玻璃板模型；下部支架各构件用frame单元模拟，下部梁柱支架边界设置固定约束，外侧拉杆与地面为铰接。结构有限元模型(finite element model，FEM)如图2所示。

光伏组件以倾斜状置于一组拉索上，拉索与光伏组件间用不锈钢夹具固定，建模时通过weld节点束缚耦合连接点的平移自由度来模拟夹具作用。

拉索初始预张力H0为30 kN，通过cable单元目标力的方式迭代施加。荷载施加顺序为拉索预张力、光伏组件自重荷载与外荷载。

根据《光伏发电站设计规范》(GB 50797—2012)[11]，在进行非抗震设计时，荷载基本组合考虑恒载、风荷载、雪荷载和温度荷载，荷载组合系数值如表2所示。

表1 材料属性Table 1 Material properties

图2 单层悬索光伏支架有限元模型图Fig.2 The FEM of single-layer cable-suspended photovoltaic support

表2 荷载效应组合Table 2 Load effect combination

1.3 数值模型验证

为验证整体有限元模型的正确性，用相同方法建立单索模型，如图3所示。参考文献[12]中的解析法对单索模型进行验证。光伏组件通过四点处夹具传递荷载至拉索上，局部构造形式如图4所示，当光伏组件沿索长分布数大于3时，竖向荷载按沿跨度均布计算内力和位移与按集中荷载计算误差在5%以内[13]，因此，可将集中荷载等效为均布的线荷载。

取初始均布线荷载为拉索自重q0(x)=7.748 N/m，再增加光伏组件自重荷载，此时荷载状态为q(x)=60.748 N/m，荷载作用下单索的水平张力H为

(1)

式(1)中：E为拉索弹性模量；A为拉索截面面积；H0为初始预张力。

有限元模拟结果与规范中解析法的对比结果见表3，两者计算结果误差在2%，验证了该模型的正确性，证明模型可用于分析单层悬索柔性光伏支架整体模型的受力情况。

q为拉索自重；H为水平张力；L为支架间距图3 单索计算简图Fig.3 Simplified calculation of single cable

图4 光伏组件连接构造图Fig.4 Connection of photovoltaic module

表3 有限元结果与解析法所得单索水平力对比Table 3 Comparison between the finite element results and the horizontal force of single cable obtained by analytical method

2 整体结构静力分析

考虑光伏组件对拉索的作用，对单层悬索光伏支架进行整体受力分析，主要分析指标选取边梁的弯矩、挠度、拉索最大变形以及光伏组件最大应力。

2.1 光伏组件应力计算及容许值

单玻光伏组件由上层玻璃盖板、醋酸乙烯酯(ethylene vinyl acetate，EVA)胶、硅电池片、EVA胶、聚氟乙烯复合膜(TPT)背板通过高温层压组成。其中，硅电池的应力状况对光伏组件的发电转化效率有着直接影响。由于对每块光伏组件都进行分层精细化建模会使得计算效率过低，故先采用纯玻璃模型进行试算，再将计算结果中挠度或应力最大的组件改用精细分层壳单元模拟，以得到硅电池片的最大应力。

硅材料是一种典型的脆性材料，其断裂应力有着较大的离散性，因此，目前常用韦伯(Weibull)分布函数统计硅的断裂应力分布情况，表达式为

Pf(σ)=1-e-(σ/σθ)m

(2)

式(2)中：Pf()为破坏概率函数；σθ为特征强度；m为韦伯模量。

实验研究[14]表明，单晶硅太阳能电池板承受与母线平行的荷载时，其特征强度为96.4 MPa，韦伯模量为14.7，所以在95%置信区间内单晶硅的容许应力为78.76 MPa。

2.2 计算结果与分析

两侧边梁在各工况下弯矩与挠度的有限元计算结果绘制如图5所示，两侧边梁弯矩与挠度基本一致，在工况JX3时最大，分别为204 kN·m和14.8 mm；工况JX5时最小，分别为120 kN·m和10.5 mm。然而，由于拉索需要较大的预张力，边梁的位移会使得拉索预应力的损失增加，加剧对结构的负面影响。

传统的光伏支架中，光伏组件固定在刚性的横梁及檩条上，其位移较小。而对于柔性光伏支架，由于光伏组件直接铺设于会产生大变形的拉索上，拉索的竖向变形会导致光伏组件的变形，从而影响光伏组件的正常使用。

由图6可以看出，在各工况下每跨拉索的变形基本一致，除受到风吸力荷载时会产生向上的位移外，其余工况均产生向下的变形。向下最大位移发生在工况ZC3下，位移值为212 mm；向上最大位移发生在工况ZC2下，位移值为81 mm。同时，在各工况下，由于光伏组件具有角度，同组的上索的挠度均大于下索的挠度，说明上索的荷载效应要更大。

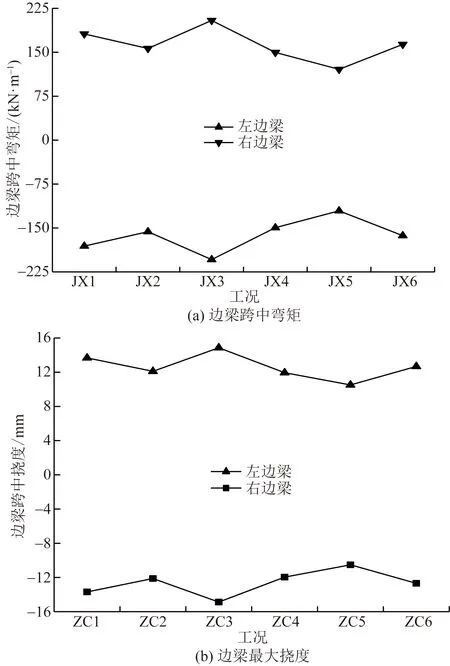
图5 两侧边梁在各工况下弯矩与挠度Fig.5 Bending moment and deflection of boundary beams under various conditions

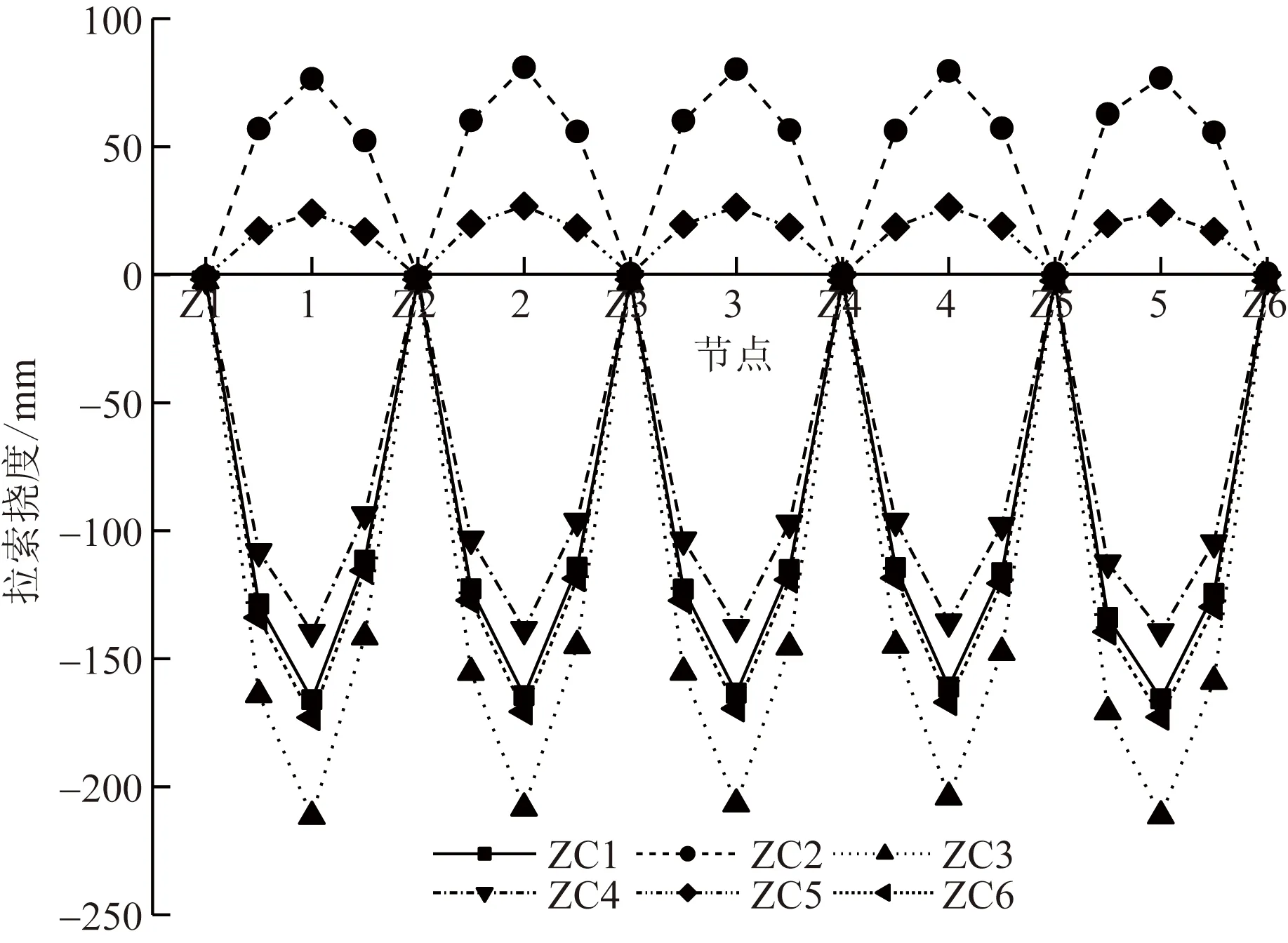
图6 拉索竖向变形Fig.6 Vertical deformation of cable

光伏组件在受荷时，存在两个方向的主应力，但由于其在受到与母线平行的荷载时更容易破坏产生隐裂，造成发电效率的降低，所以主要分析其与母线平行的第一主应力。从整体看，组件的最大应力发生在与拉索的固定连接处，并向中心处逐渐减少；从各层材料看，材料的最大应力发生在长边中心，并向组件中心逐渐减少。从表4可知，光伏组件在正常使用时硅片层的最大应力发生在工况3下，此时应力尚在容许应力以内，没有产生断裂。

表4 光伏组件应力计算结果Table 4 Stress calculation results of photovoltaic modules

3 影响因素分析

3.1 拉索预张力

拉索的预张力对于结构的受力性能有着至关重要的影响。较大的拉索预张力能够减小拉索挠度，但同时会对其端部支承结构产生较大的水平力，从而使主梁和拉杆端部节点的受力加大，进一步导致端部位移加大，危害结构的整体稳定性；而较小的拉索预张力虽然对端部的支承结构影响较小，但会使得拉索的竖向挠度较大，从而导致光伏组件变形过大，甚至损坏，影响光伏组件的光电转换效率。因此，有必要分析在两种最不利工况下不同预张力对结构计算的影响。

由图7可知，当拉索预张力较小时，边梁的弯矩及挠度较小，增加预张力可以显著减小拉索的跨中挠度，但会显著增大边梁的受力，且预张力超过30 kN后，拉索挠度减小幅度放缓，故不能仅靠增大拉索预张力作为减少挠度的方法。

3.2 钢架间距

在减小拉索挠度时，除了考虑预张力，钢架间距的影响同样不可忽视。钢架间距的改变对拉索的挠度有着显著的影响。不同钢架间距下拉索变形如图8所示。

随着间距的增加，拉索的最大挠度有着明显的增大。在跨度较小时，增大预张力对控制拉索的竖向挠度并无太大影响，反而会加大对下部支撑的水平拉力，导致拉索在使用中的预应力损失增大；当跨度较大时，较大的预张力可以显著减小拉索跨中挠度，从而减小组件的变形。跨度超过20 m后，随着跨度增加，拉索跨中挠度增速加快。因此，结合拉索预张力的影响考虑，结构跨度在15～20 m时，拉索和边梁的受力状态较为合理。

3.3 光伏组件支承方式

由于光伏组件是四点支承于拉索上，不同的边界约束对光伏组件的受力情况影响显著。考虑两角点放松轴向自由度以及四角点均约束3个平动自由度两种支承情况，即支承方式一和支承方式二，形式如图9所示。

以控制变量法研究光伏组件的两种支承方式对光伏组件受荷时应力的影响，组件的分层精细化模型计算结果见表5。可以看出，两种支承情况下玻璃层的最大应力相差较小，但支承方式一的硅电池层的最大应力在6种工况下均小于支承方式二，并且在工况ZC6下硅的应力减小幅度最大为47.8%。这是由于索的拉伸使组件受到沿索轴向的附加应力，该应力与其他应力叠加导致了组件应力增大。因此，为了优化光伏组件正常使用时的最大应力，光伏组件的支承方式建议采用方式一，即放松光伏组件两角点沿拉索轴向自由度。

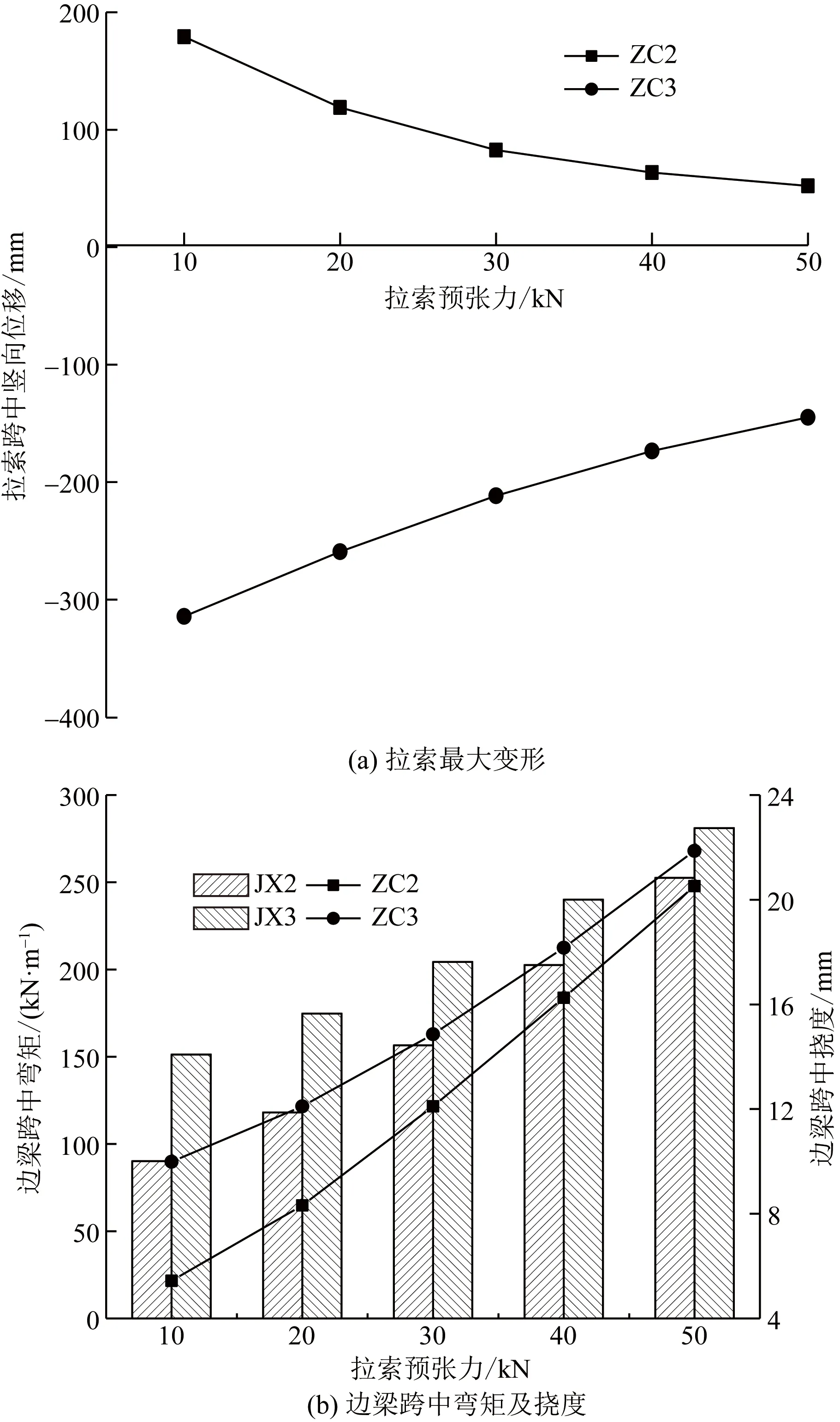
图7 不同预张力下结构计算结果Fig.7 Calculation results under different pretensions

图8 不同钢架间距下拉索变形Fig.8 Cable deformation under different rigid frame spacing

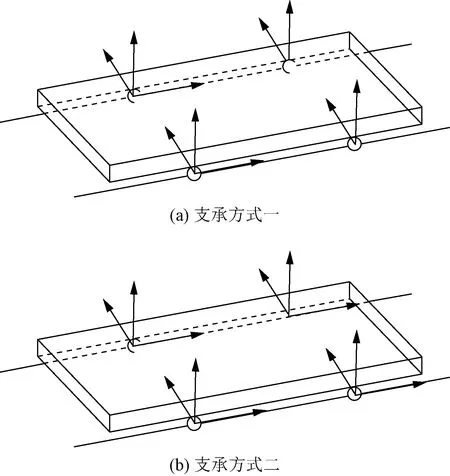
图9 光伏组件不同支承形式Fig.9 Different supporting forms of photovoltaic modules

表5 光伏组件计算结果Table 5 Calculation results of photovoltaic modules

4 简化计算方法

为探索在竖向荷载作用下，拉索的受力及变形情况，考虑边梁支座在拉索水平力作用下的位移，提出一种简化计算方法。

4.1 基本假定

由前文分析可知，单层悬索柔性光伏支架在初始和受荷后的垂度较小，为简化研究，突出主要问题，现对其做以下假定[15]：①拉索为理想柔性，材料力学特性符合胡克定律；②拉索在自重及受荷时线形曲线为抛物线；③拉索的质量沿索弦向均匀分布；④拉索所受荷载等效为均布分布。

4.2 计算公式推导

由整体分析可知，计算多跨连续单索时，由于中间支架与拉索滑动位移很小，可忽略，且各跨拉索位移情况相似，因此在简化计算模型时暂不考虑其位移，并将其等效为单跨拉索计算，再将边梁等效为定向弹簧支座，考虑其在拉索张力下的位移Δ，计算模型如图10所示。

根据图10，可求得拉索无应力长度S为

S=S1-ΔS

(3)

式(3)中：S1为拉索受荷后的长度；ΔS为拉索伸长量。

变形前拉索形状公式为

(4)

设受荷变形后拉索形状公式为

(5)

取拉索变形后某处索段微元体进行受力分析，如图11所示。

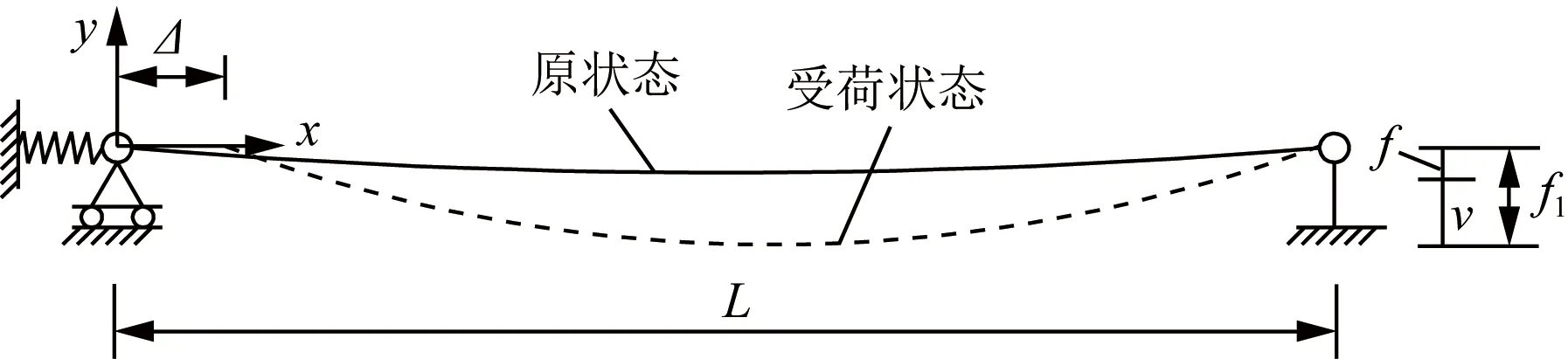
f为拉索变形前的垂度；f1为拉索受荷变形后的垂度；Δ为支座位移 量；v为跨中挠度图10 拉索简化计算模型Fig.10 Simplified calculation model of cable

T1为受荷时拉索拉力图11 微元体计算模型Fig.11 Calculation model of microelement

将受荷后的索段长度S1用微分形式表示为

(6)

将式(6)进行积分并代入式(3)可得

(7)

将式(7)中拉索原长S用微分形式表示，并利用泰勒级数展开取前两项可得

(8)

由于拉索的伸长是由索内力增量所引起，即可得

(9)

式(9)中：T为原状态拉索拉力。

因此将式(8)、式(9)代入式(7)可得

(10)

由此可求得跨中挠度值v为

v=f1-f

(11)

弹簧支座的位移Δ是边梁受荷后的侧移量。现对位移Δ进行求解，其值与下部支承情况以及拉索拉力有关。现以单跨简支梁为例，由于边梁上有多组成对的拉索水平力，将其等效为均布荷载，建立计算模型，如图12所示。

i、j为坐标轴；l为边梁长度；qH为拉索水平力均布荷载图12 边梁计算模型Fig.12 Calculation model of side beam

由于拉索在边梁处夹角较小，因此忽略其对边梁的竖向作用，不考虑边梁的竖向位移，仅考虑其沿拉索轴向的支座位移Δ。

拉索在受荷时水平拉力计算公式为

(12)

式(12)中：H1为受荷时拉索水平力；q为拉索所受活荷载；w为拉索原状态所受荷载。

根据式(12)计算出受荷时拉索水平力H1，再利用水平力计算出支座位移Δ。

(13)

(14)

式中：n为拉索根数；E为边梁弹性模量；I为边梁截面惯性矩。

先根据初始水平力H求得垂度f，而后，根据式(14)求出支座位移Δ，将Δ代入式(5)及式(10)求出f1，从而得到受荷时的拉索线形表达式。再同以上步骤迭代得到最终结果，由于拉索垂度较小，需要进行两次迭代。

5 工程实例验证

工程是湖南长沙某水质净化厂分布式光伏发电项目。光伏场区占地面积约38 100 m2。由于场地限制，传统光伏支架不能满足下部水池使用，故选用单层悬索柔性光伏支架，结构体系如图13所示。

本工程结构安全等级为二级，设计使用年限为25年。地面粗糙度为B类，建筑抗震设防类别为丙类，抗震设防烈度为6度，设计地震分组为第一组，场地类别为Ⅱ类。基本风压为0.35 kN/m2，基本雪压为0.45 kN/m2，单块光伏组件自重为0.20 kN。现以实际工程参数代入有限元模型及简化计算方法中进行计算。

取从边跨往右第二组拉索中的下索，分析其在各种荷载工况下的跨中拉索位移最大值，有限元模拟结果与本文简化计算理论解的对比见表6。

可以看出，两者计算结果相近，简化计算结果较有限元模拟偏大，除荷载工况ZC2和ZC4下拉索向上位移具有较大误差外，剩余误差均在5%左右，表明简化计算结果偏于安全，故所给简化计算方法可用于分析单层悬索柔性光伏支架中拉索的线形及跨中挠度。

图13 单层悬索光伏支架Fig.13 Single-layer cable-suspended photovoltaic support

表6 拉索最大位移Table 6 Maximum displacement of cable

6 结论

对单层悬索光伏支架整体结构进行了详细分析，研究了下部支架、光伏组件以及拉索的受力情况。在考虑支座位移的条件下，对单层悬索光伏支架结构的拉索受荷变形进行公式推导。最后，结合工程实例对简化计算方法进行验证，得到以下结论。

(1)单层悬索光伏支架在荷载作用下，两侧边梁的受力和变形情况一致；同组拉索中上索的挠度均大于下索的挠度；光伏组件受背风荷载作用时，拉索会产生向上变形，其最大位移为81 mm；其余工况均产生向下的变形，且各跨变形一致，最大位移为212 mm。

(2)拉索预张力越大，拉索跨中挠度越小，两侧边梁受力越大；钢架间距越大，拉索跨中挠度越大。当钢架间距在15～20 m，拉索预张力推荐取值为30～40 kN。同时，为避免硅电池片隐裂导致的发电效率降低，可以通过释放其一侧沿拉索轴向约束的方式减小其应力最大值。

(3)基于抛物线理论提出了一种考虑支座位移的拉索线形简化计算方法。同时，结合工程实例对该方法进行了验证，简化计算方法的结果与有限元计算偏差约5%。简化计算方法结果偏于安全，可用于单层悬索光伏支架的初步设计。