永磁同步电机改进模糊超螺旋滑模观测器设计

王亚召， 何山，2*， 程静，2

(1. 新疆大学电气工程学院， 乌鲁木齐 830046； 2. 可再生能源发电与并网控制教育部工程研究中心， 乌鲁木齐 830046)

永磁同步电机(permanent magnet synchro-nous motor，PMSM)因体积小、气隙磁通密度高、可靠性好等优势被广泛应用于各种工控领域[1-2]。在PMSM各种控制方式中，都需使用转子位置和转速信息。采用机械式位置传感器获取转子位置和转速的方式较简单，但其故障率高、投入成本大，故无位置传感器技术获得广泛的关注[3-4]。同时滑模观测器因其具有计算简单、受参数摄动影响小、鲁棒性好、收敛速度快等优点被广泛采用。

传统一阶滑模观测器中使用符号函数会导致严重的抖振问题，在提取反电动势时需使用低通滤波器进行滤波，低通滤波器的使用会增加系统复杂度[5-6]。文献[7]提出一种二阶非奇异终端滑模观测器观测两相静止坐标系下定子磁链，减轻抖振的同时能使系统状态快速收敛，但未考虑测量磁链初始误差对观测结果的影响；文献[8]使用超螺旋滑模观测器来削弱一阶滑模观测器中的抖振问题，减少低通滤波器使用，且不需要额外加入角度补偿算法，但其采用固定滑模增益，抗干扰能力有限；文献[9]提出一种离散型变增益的超螺旋滑模观测器，提高观测速域，但同时系统复杂性增加，应用范围有限；文献[10]提出一种在自适应调整超螺旋滑模增益的方法，抗干扰能力强，但自适应律难以确定，收敛速度慢；文献[11]通过模糊控制器获得上界函数，提高系统的鲁棒性及精度，但计算量较大；文献[12]采用模糊控制器整定滑模增益，同时采用两级滤波结构抑制反电动势中的谐波分量，但增加系统成本，降低系统稳定性；文献[13]使用反向传播的神经网络算法在线优化超螺旋滑模观测器的滑模增益，虽能提高系统观测精度与鲁棒性，但算法需要设计的参数较多。

现采用归一化前馈锁相环来提取转子位置和转速，避免观测器在转速斜坡变化时误差累积。针对传统超螺旋滑模观测器使用固定滑模增益时高频抖振、鲁棒性差的问题，采用模糊控制器对滑模增益自整定以削弱抖振，提高系统对外界抵抗能力及内部参数摄动的鲁棒性。最后仿真验证所提策略的有效性。

1 数学模型

表贴式永磁同步电机在α-β两相静止坐标系下的数学模型为

(1)

式(1)中：uα、uβ分别为α轴和β轴定子电压；Rs为定子电阻；iα、iβ分别为α轴和β轴定子电流；Ls为定子电感；eα、eβ分别为α轴和β轴反电动势，定义为

(2)

式(2)中：ωe为电机转子电角速度；ψf为永磁体磁链；θe为电机转子位置角。由式(2)可知，反电动势包含电机实时转子位置角和转速信息。

2 改进模糊超螺旋滑模观测器

2.1 传统超螺旋滑模观测器

超螺旋滑模本质为二阶滑模，它通过与高阶滑模函数串联，在一定程度上能减轻传统滑模观测器中使用符号函数带来的抖振问题，提高观测精度。选择定子电流作为系统状态变量，反电动势作为未建模变量，观测误差，构建超螺旋滑模观测器如下。

(3)

用式(3)减去式(1)得

(4)

根据等效控制原则有

(5)

由式(2)可知，使用反正切函数可从反电动势中获得转子位置和转速信息，即

(6)

(7)

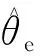
(8)

式(8)中：ε为正数。

2.2 归一化前馈锁相环

当PMSM转速恒定时，使用传统锁相环能取得良好的转子位置跟踪效果；当PMSM转速斜坡变化或阶跃变化时，采用传统锁相环会导致转子位置估计值存在稳态误差。故采用一种归一化前馈锁相环改善速度动态变化时观测精度，归一化前馈锁相环框图如图1所示。

图1 归一化前馈锁相环Fig.1 Normalized feedforward phase-locked loop

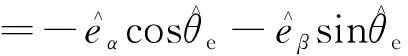
=kΔθe

(9)

(10)

归一化前馈锁相环的闭环传递函数为

(11)

式(11)中：s为复变量；ωc为前馈路径中低通滤波器截止频率；kp、ki分别为PI控制器比例、积分系数。

其误差传递函数为

(12)

式(12)关于s在0点附近的泰勒展开式为

H(s)=C0+C1s+C2s2+C3s3+o(s3)

(13)

当转速为阶跃或斜坡输入时，归一化前馈锁相环的稳态误差为

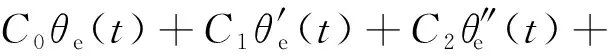
C3θ′′′e(t)+o[θ′′′e(t)]=0

(14)

由式(14)可知，当速度为斜坡输入时，归一化前馈锁相环稳态跟踪误差为0。

2.3 模糊超螺旋滑模观测器

模糊控制[16]是一种将专家的经验、知识转换成模糊语言进行高性能控制的智能控制算法，其不依赖系统模型，具有强鲁棒性和自适应性。

(15)

式(15)中：λ为中间增益，正数。

选定模糊控制器输入的论域为[-3 3]，输入量模糊语言划分为{NB(负大)，NS(负小)，ZO(零)，PS(正小)，PB(正大)}，输出论域设置为[-4 4]。输出量模糊语言划分为{NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)，PB(正大)}。采用Mamdani模糊推理算法和重心法反模糊化。

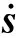
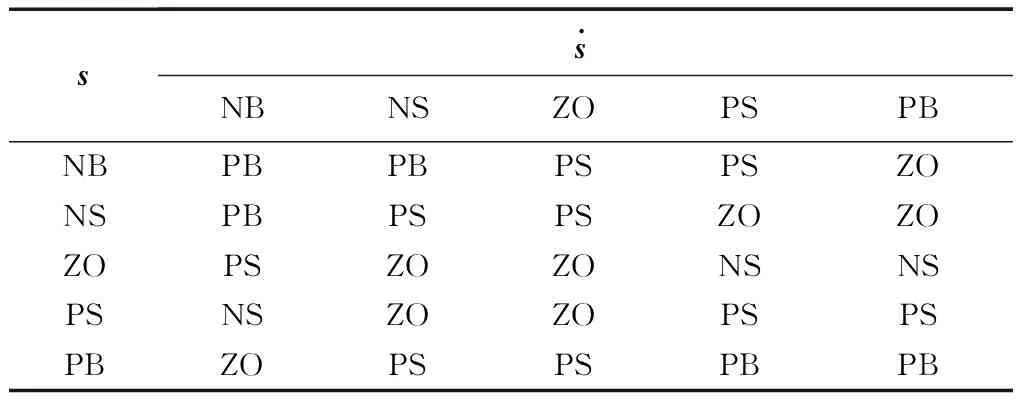
表1 模糊控制规则Table 1 Fuzzy control rule

2.4 稳定性分析

根据Lyapunov定理，选择状态变量为

(16)

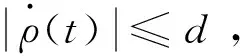
(17)

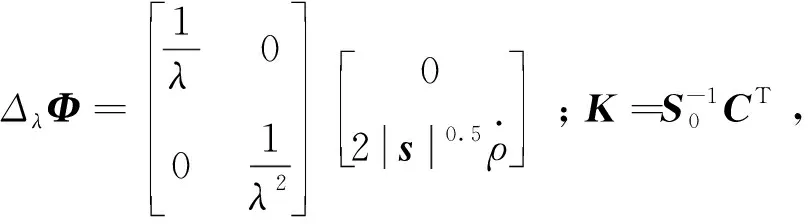
S0+ATS0+S0A-CTC=0

(18)

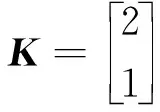
式(18)为系统到达滑模面之前的情况，根据Lyapunov函数有

V(ξ)=ξTS0ξ

(19)

则V(ξ)沿着式(19)轨迹的时间倒数为

(-ξTS0ξ+ξTCTCξ+2ξTS0ΔλΦ)

(20)

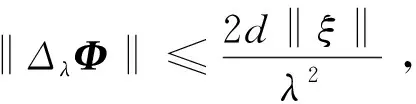
(21)

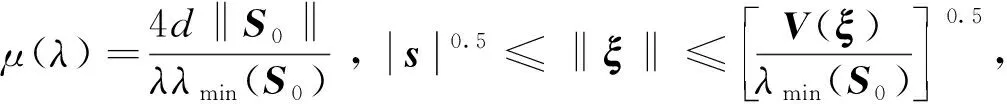
(22)

选择足够大的λ使得不等式成立，即

λ≥μ(λ)

(23)

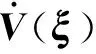
(24)

因此，状态变量ξ1和ξ2在有限时间内收敛到零。由式(24)可知，选择足够大的增益λ可以缩短收敛时间。λ的选择条件为

(25)

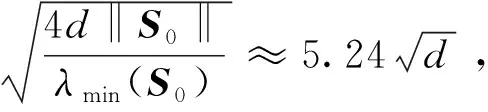
3 仿真分析

为验证所提策略有效性，在MATLAB/simul-ink中搭建PMSM仿真模型，采用id=0矢量控制策略，系统整体框图如图2所示，并与传统STSMO进行对比。PMSM参数如表2所示。

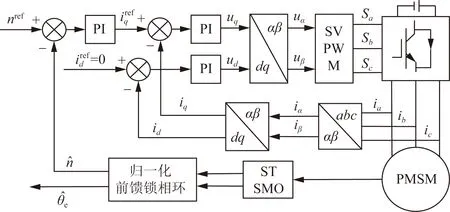
图2 系统整体框图Fig.2 The overall block diagram of system

表2 PMSM参数Table 2 Parameters of PMSM

在仿真实验中，将传统STSMO与所提出的改进模糊STSMO进行对比。在0 s时空载启动，给定阶跃转速400 r/min。为了验证转速变化的情况下所提策略对转子位置及转速的观测效果，在0.1～0.3 s时，将给定转速从400 r/min提升至800 r/min，在0.4 s时将负载转矩阶跃至2 N·m。对转速n、转子位置角θe、q轴电流波形进行分析；为了验证参数摄动对观测性能的影响，在0 s时给定800 r/min的阶跃转速，分别对比两种观测器在电阻、电感参数摄动时转速观测精度。

3.1 转速跟踪对比

两种策略下转速跟踪波形如图3和图4所示，仿真实验数据如表3所示。

由图3可知，传统STSMO策略下采用反正切函数提取观测转速，即使额外附加补偿措施，仍存在较大稳态误差且存在误差累积现象；由图4可知，改进模糊STSMO策略中采用归一化前馈锁相环，PMSM加速时转速观测误差累积。使用模糊控制器实时调整滑模增益，观测器具有较强的转速跟踪能力，抖振现象得到有效抑制。

由图3、图4及表3可知，改进模糊STSMO策略下，负载突变时转速超调量得到抑制，且动态响应速度更快。在传统STSMO策略下，在负载突变时，由于转速的超调使扰动变大，使得系统存在较大观测误差。

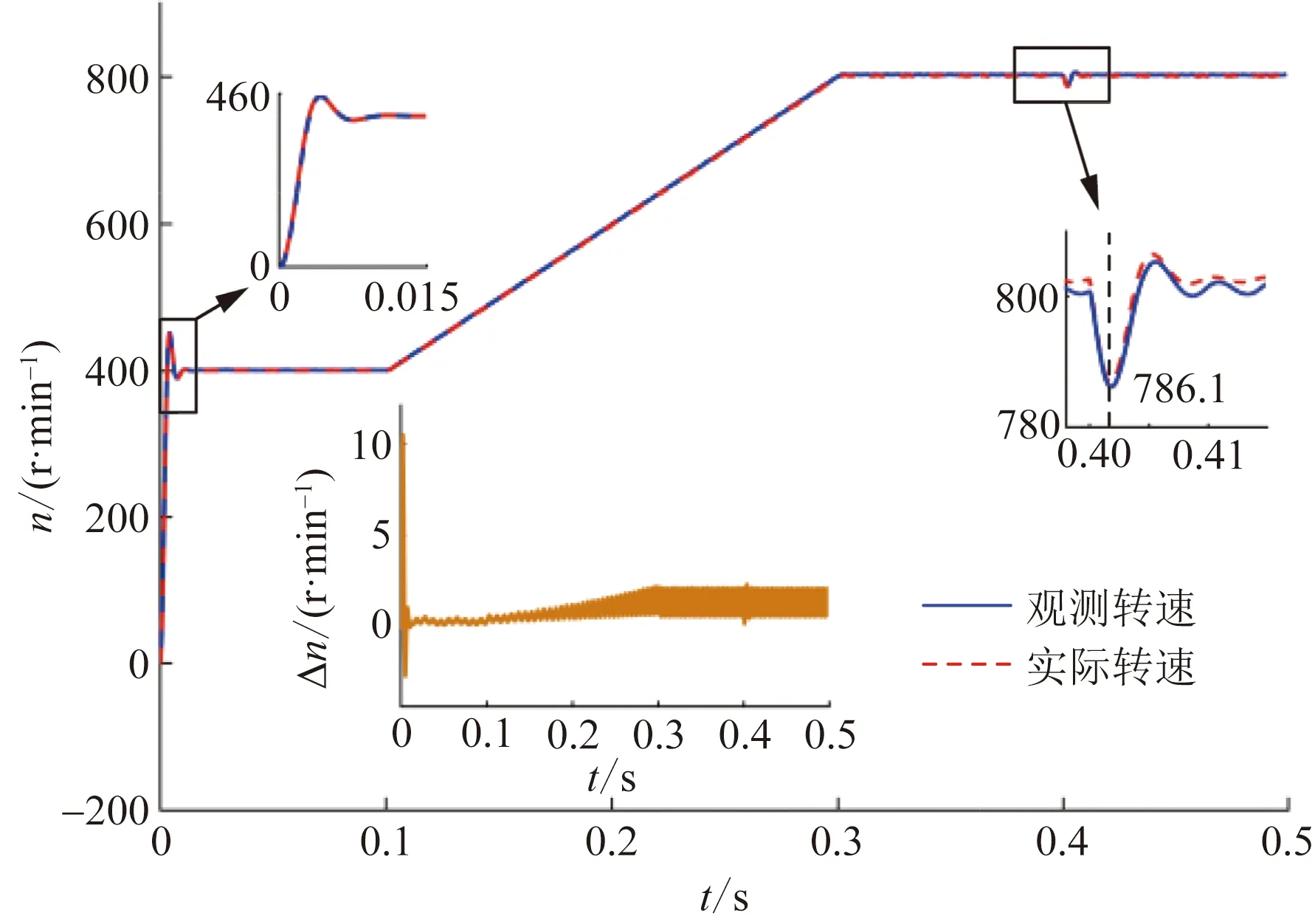
图3 传统STSMO转速Fig.3 Rotating speed of the conventional STSMO

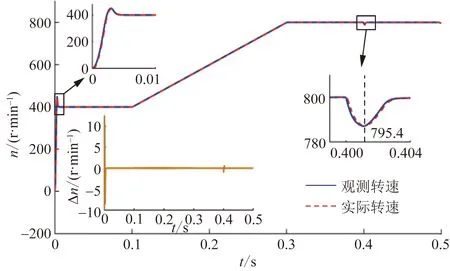
图4 改进模糊STSMO转速Fig.4 Rotating speed of the improved fuzzy STSMO

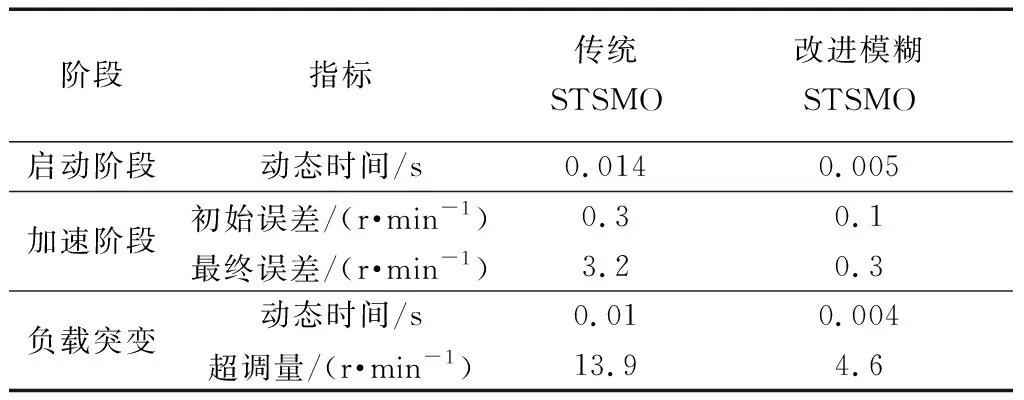
表3 转速仿真数据Table 3 Rotating speed simulation data

3.2 转子位置跟踪对比

两种策略下转子位置跟踪波形如图5和图6所示，仿真实验数据如表4所示。

由图5可知，在启动阶段，传统STSMO策略下转子位置误差较大，在PMSM加速过程中，转子位置观测误差随着转速的增大而增加；由图6可知，在改进模糊STSMO策略下，启动阶段转子位置观测误差在0.01 rad以内，在中低速至高速阶段转速观测误差保持在0.001 rad之内，精确观测转子位置可以为双闭环控制提高准确的转子位置信息。

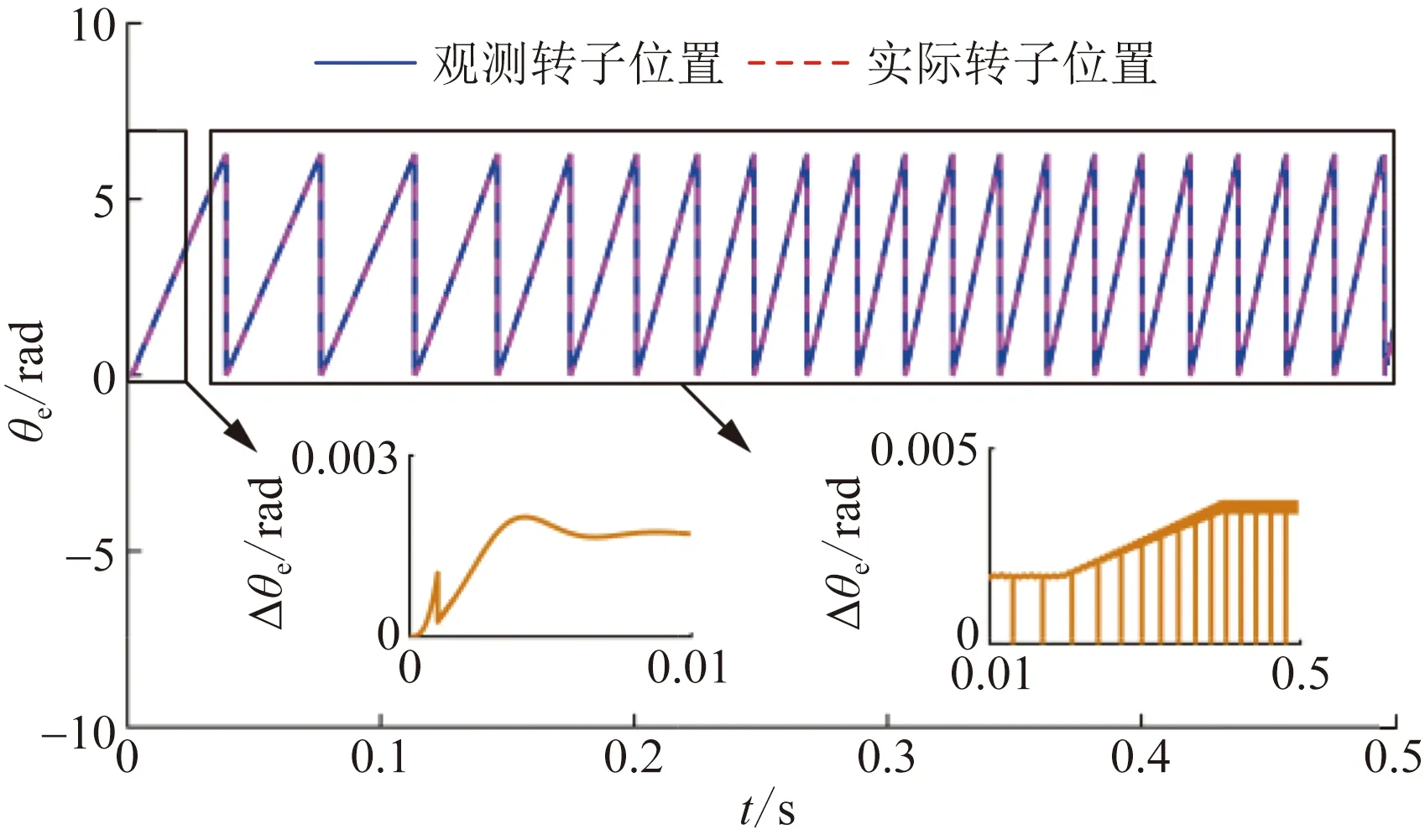
图5 传统STSMO转子位置Fig.5 Rotor position of the conventional STSMO

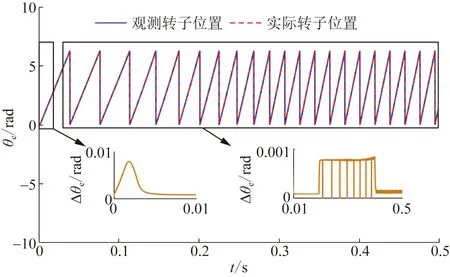
图6 改进模糊STSMO转子位置Fig.6 Rotor position of the improved fuzzy STSMO

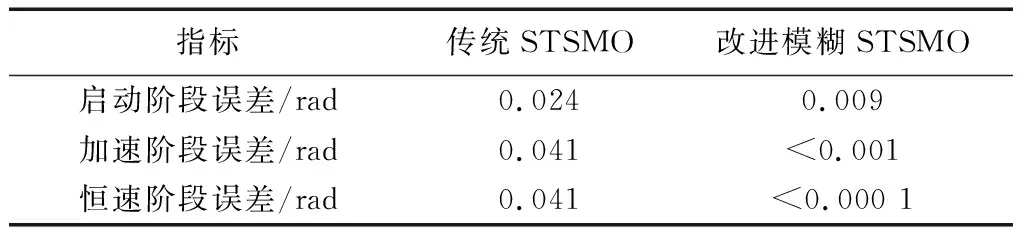
表4 转子位置仿真数据Table 4 Rotor position simulation data

3.3 q轴电流响应对比

两种策略下q轴电流响应波形如图7和图8所示，转矩仿真实验数据如表5所示。

由图7可知，传统STSMO策略下在启动及负载转矩突变时q轴电流经过连续振荡衰减后逐渐稳定，动态响应时间较长；由图8可知，改进模糊STSMO策略中利用模糊控制器调整滑模参数，系统抵抗外部干扰能力强，动态响应速度加快。

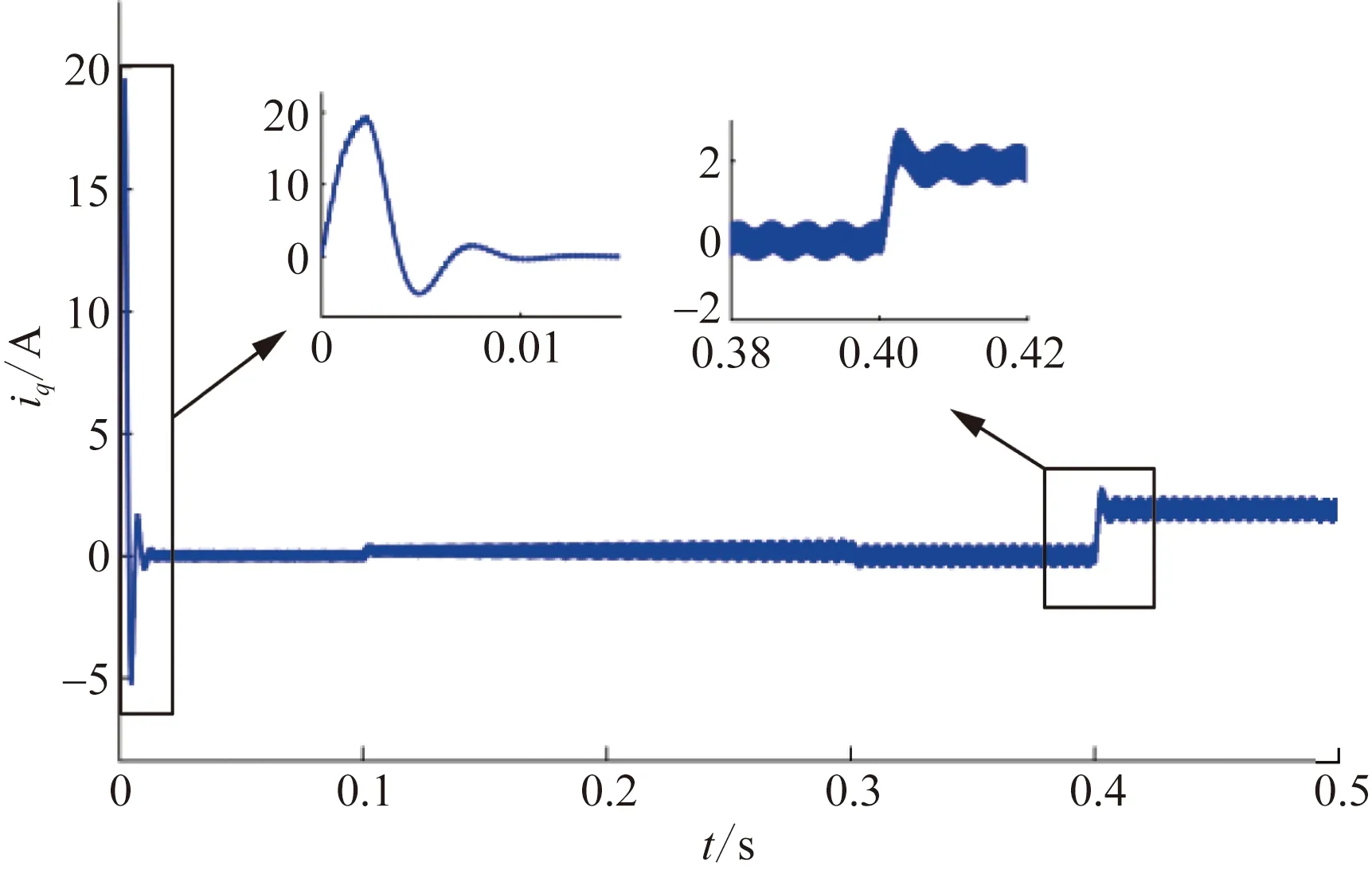
图7 传统STSMO中q轴电流波形Fig.7 Current waveform of q-axis in conventional STSMO

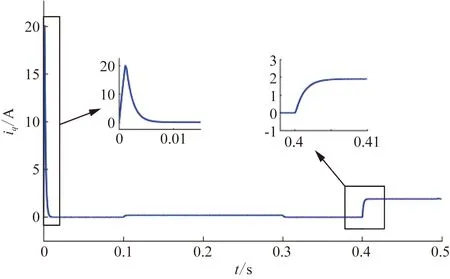
图8 改进模糊STSMO中q轴电流波形Fig.8 Current waveform of q-axis in improved fuzzy STSMO

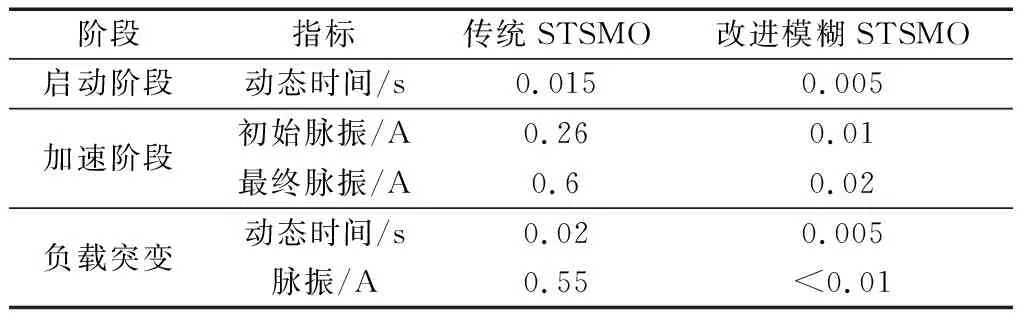
表5 q轴电流仿真数据Table 5 Current simulation data of q-axis

由图7可知，在0.1～0.3 s转速斜坡给定时，传统STSMO策略中q轴电流脉振现象随着转速的升高而加剧。在电机加速过程中，电流脉振不断累积，在0.4 s负载转矩阶跃变化时，iq脉振为0.55 A。iq电流脉振会导致电磁转矩响应中含有较大脉振，影响系统性能；由图8可知，改进模糊STSMO策略中q轴电流波形较为平稳，在0.1～0.3 s转速斜坡给定时电流脉振稳定在0.02 A以内，带载时电流脉振小于0.01 A。

3.4 参数摄动工况对比

在0 s时给定阶跃转速800 r/min，分别对比分析电阻、电感各增加20%时两种观测器转速跟踪情况。

3.4.1 电阻参数摄动对比

电阻参数升高20%时，两种观测器转速跟踪波形如图9和图10所示，仿真数据统计如表6所示。

由图9可知，传统STSMO采用固定滑模增益，系统鲁棒性较差，电阻参数摄动时，传统STSMO策略下转速观测误差达5.2 r/min，观测转速精度较低，抖振大；由图10可知，改进模糊STSMO策略下根据系统状态实时调整滑模增益，转速观测误差为1.1 r/min，观测精度高，抖振小，电阻参数摄动时鲁棒性优于传统STSMO。

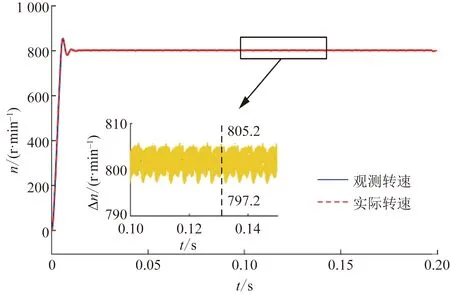
图9 传统STSMO转速波形Fig.9 Rotating speed waveform of conventional STSMO

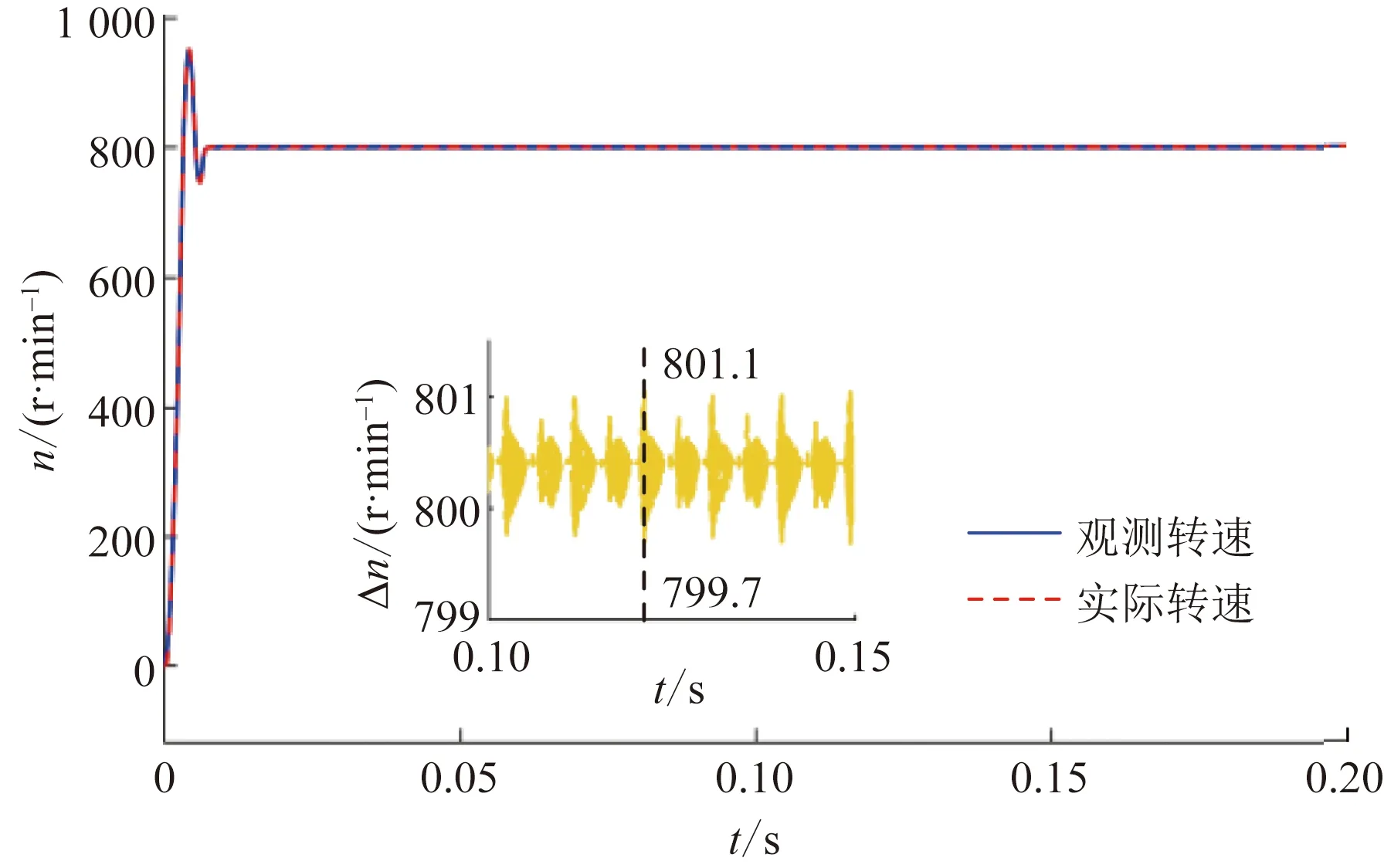
图10 改进模糊STSMO转速波形Fig.10 Rotating speed waveform of improved fuzzy STSMO

表6 电阻升高变化时转速仿真数据Table 6 Simulation data of rotating speed when resistance changes

3.4.2 电感参数摄动对比

电感参数升高20%时，两种观测器转速跟踪波形如图11和图12所示，仿真数据统计如表7所示。

由式(1)可知，相较于电阻参数摄动，PMSM电机对电感参数摄动更敏感。由图11可知，电感升高20%时，传统STSMO策略下转速跟踪误差达22.8 r/min，抖振较大；由图12可知，电感参数升高20%时，改进STSMO策略下转速观测误差为6.1 r/min，观测器对电感参数摄动鲁棒性强。

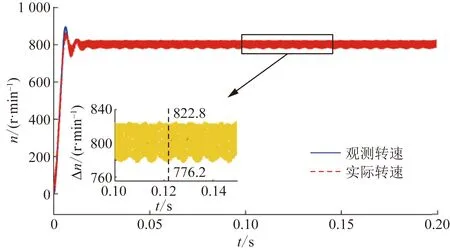
图11 传统STSMO转速波形Fig.11 Rotating speed waveform of conventional STSMO

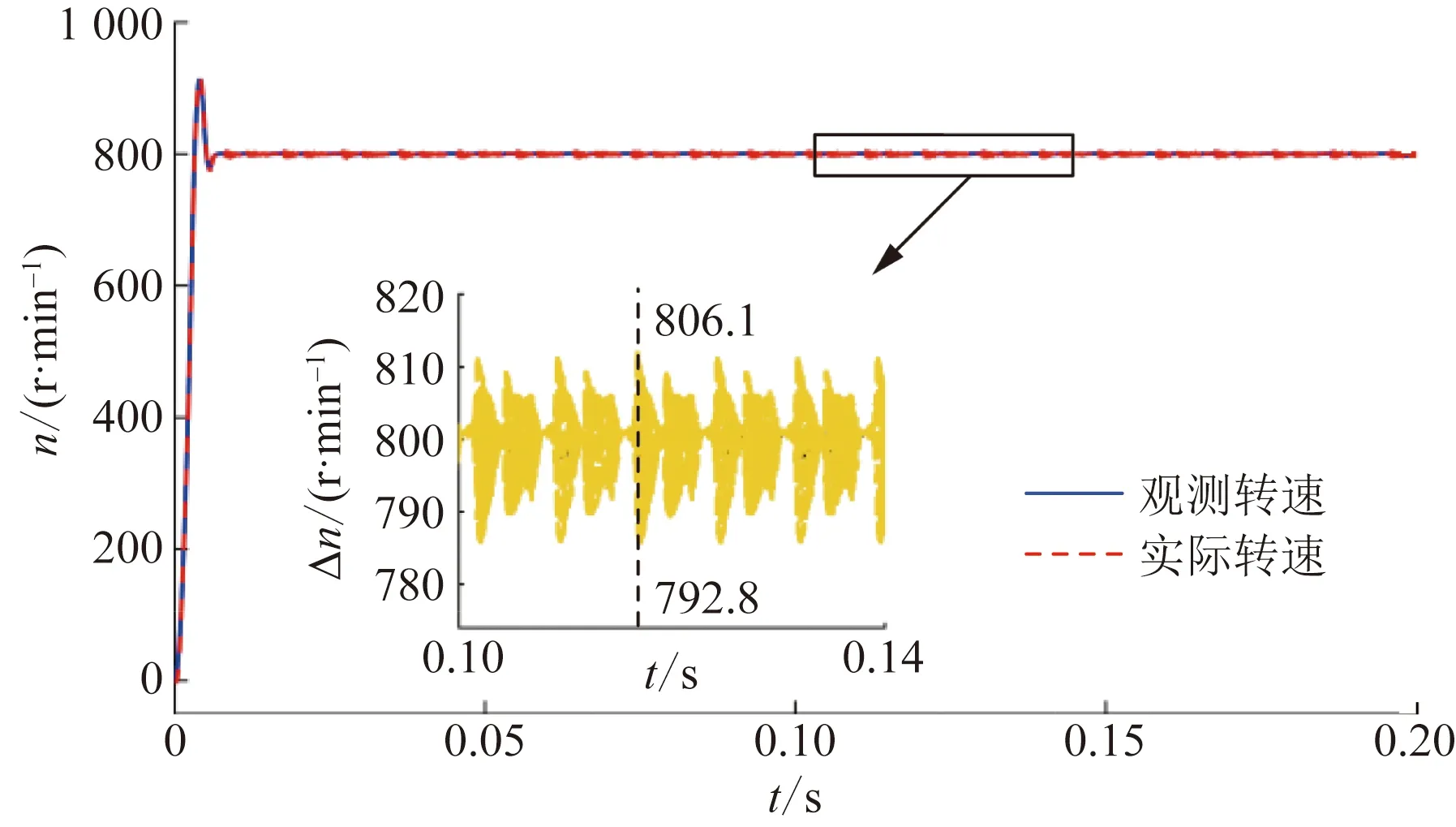
图12 改进模糊STSMO转速波形Fig.12 Rotating speed waveform of improved fuzzy STSMO

表7 电感变化时转速仿真数据Table 7 Simulation data of rotating speed when inductance changes

4 结论

设计了一种改进模糊超螺旋滑模观测器，通过与传统超螺旋滑模观测器在转速动态变化、负载扰动及内部参数摄动扰动工况下进行对比，得出以下结论。

(1)通过运用归一化前馈锁相环提高观测器在转速动态变化阶段观测精度，避免观测误差累积现象。

(2)通过模糊控制器在线整定滑模增益，削弱观测抖振，提高系统整体观测精度，并且减少系统动态响应阶段超调时间。

(3)模糊规则的引入提高系统的鲁棒性，相较于固定滑模增益的传统STSMO策略，观测器抗干扰能力增强，在外部负载扰动、内部参数摄动时能够有效跟踪实际转速。