基于位置闭环的模糊PID起落架控制系统研究

智 鑫,张明远

(沈阳工业大学 机械工程学院，辽宁 沈阳 110870)

0 引言

直升机仿生起落架由于自身适应性广而得到广泛关注[1]，起落架控制系统则是仿生起落架运动的核心。但起落架控制系统目前还处于发展阶段，调节速度慢、鲁棒性低、控制精度不高成为控制系统发展的主要阻碍。解决控制系统上述问题成为起落架控制系统研究的一大热点。

为了解决起落架控制效率的问题，国内外学者对其进行了大量研究。国外学者Boix[2]、Sarkisov[3]等为了解决起落架控制效率问题，提出一种基于角度变化的起落架PID控制系统，通过惯性元件测量起落架倾角，运用PID控制器调节起落架支腿以消除角度误差，实现起落架平衡调节，该控制系统有效提高了起落架的控制精度，增加了系统的稳定性。国内起落架控制系统的研发相对较晚，但仍取得了较大突破。Huang Mingyang[4]、Hu D[5]等学者设计了一种基于位置闭环的起落架控制系统，通过红外测距仪测量起落架离地距离，基于位置信息通过控制器控制电机旋转实现控制系统的预调。仿真结果表明，该控制系统结构简单，控制效率高，但PID控制器需要准确的数学模型，且当发生突变情况时，PID控制器将失去稳定性。

本文针对目前起落架控制系统存在的控制效率低、控制精度不足、鲁棒性差等问题，设计一种基于位置闭环的模糊PID起落架控制系统，首先使用改进卡尔曼滤波对超声波测距进行滤波，然后基于位置信息通过模糊PID控制器调节起落架支腿实时位置，实现起落架迅速、平稳着陆。

1 起落架控制系统设计

本文所设计的起落架控制系统可分为3部分，如图1所示。第一部分为传感器测量部分，位于起落架膝关节的超声波检测传感器实时检测起落架支腿的位置，并将位置信息传输给控制器。第二部分为控制器计算部分，控制器将超声波测距信息进行滤波后，与系统输入的期望位置相比较，将位置误差以及误差变化率输入到模糊PID控制器中，控制器对数据进行分析，输出起落架调节的位移信息，树莓派控制器将位移信息转换为控制电机的PWM信号后输出给电机上方的电机驱动器。第三部分为硬件执行部分，电机驱动器将控制信号转换为电机的驱动信号驱动电机转动，实现起落架调节。

图1 起落架控制系统结构框架

2 位置闭环优化

2.1 改进卡尔曼滤波算法

由于噪声的影响，由超声波测距所得的信号数据波动较大，对控制系统的准确性有很大的影响，因此需要对数据进行改进卡尔曼滤波优化，以提高测距准确性。

改进卡尔曼滤波是一种根据先验预估值与当前测量值进行加权评估的算法，通过对预估值和当前测量值比较进行修改，以输出准确数值。基于改进卡尔曼滤波算法，先验估计值X=k由下式计算：

X=k=0.4Xk+0.6Xk-1f≥5X=k=Xk-1f<5.

(1)

其中：Xk为当前测量值；Xk-1为上次系统的最优值；f=Xk-Xk-1。

更新预测协方差矩阵的公式如下：

P=k=Pk-1+Q.

(2)

其中：P=k为当前系统预测协方差；Pk-1为上一次系统的最优协方差矩阵，初始值为0;Q为过程噪声协方差。

由下式计算卡尔曼增益Kg：

Kg=P=k/P=k+R.

(3)

其中：R为观测噪声协方差。

通过卡尔曼增益修正输出X-k：

X-k=X=k+Kg(Xk-Xk-1).

(4)

更新最优协方差矩阵：

Pk=(1-Kg)·P=k.

(5)

2.2 PID控制理论

尽管当前发展了许多控制理论，但是因为PID具有良好性能并且控制简单，仍然是工业控制过程中应用最多的控制理论[6]。图2为PID控制的基本流程。

图2 PID控制基本流程

PID控制器在其工作过程中根据设定目标值(Mb)与测量值(Cl)的差值e自动调整输出w，各关系如式(6)和式(7)所示：

e(t)=Mb-Cl.

(6)

w(t)=w(t-1)+Kpe(t)+KpTi∫t0e(t)dt-Tdde(t)dt.

(7)

其中：Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

2.3 模糊PID控制

传统PID控制器结构简单而且效果较好，因此成为控制的主流应用。但是比例、积分、微分控制系数一旦确定就无法更改，在一些实时变化、物理模型不确定的系统中PID调节很难收到预期的效果。因此模糊PID得到广泛关注和发展，成为控制的主要方法之一[7-9]。模糊PID控制器以经典PID控制器为基础，利用模糊推理来调节PID增益。模糊PID控制流程如图3所示，通过实时检测系统实际参数和目标值之间的误差以及误差的变化率调节PID中的增益系数，进而调节系统的输出值，以适应不同情况下的系统，因此模糊PID具有模糊系统的鲁棒性和自适应性等特点。

2.3.1 模糊化处理

模糊控制器不能直接对精确值进行分析，需要将输入的误差及误差的变化率进行模糊化处理。

首先对输入值设置模糊语言以及对应的论域。为了保证控制器的精确控制，将输入值的模糊语言设置为：正大(PB)、正中(PM)、正小(PS)、零(ZO)、负小(NS)、负中(NM)、负大(NB)。同时设置论域为[-6，6]。在MATLAB中设置隶属度函数,如图4所示。

图3 模糊PID控制流程

图4 误差e及误差变化率ec的隶属度函数

2.3.2 模糊规则

控制规则是控制器输出正确的保障，在不同输入的e、ec下，控制规则也不同。根据专家经验建立了Kp、Ki、Kd的模糊规则表，分别见表1～表3。

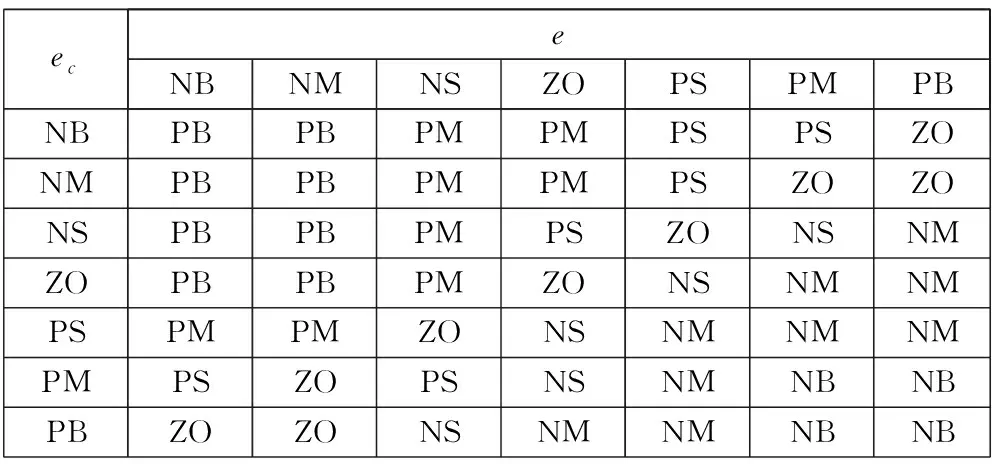
表1 Kp模糊控制规则

表2 Ki模糊控制规则

表3 Kd模糊控制规则

2.3.3 解模糊(重心法)

根据模糊规则推理之后，所得的结果仍然是模糊信息，不能直接用于控制执行结构，此时需要将得到的模糊信息进行解模糊化处理。重心法是当前最常用的方法，重心法通过计算隶属度函数和坐标轴横轴围成的面积的重心来计算相应精确值，即:

u=∫uci(z)·zdz∫uci(z)·dz.

(8)

其中：u为输出的PID控制参数：uci(z)为隶属度函数值；z为取得隶属度函数值对应的输出论域中的元素值。

计算出精确值后，即可得到模糊PID的Kp、Ki、Kd系数值。

3 仿真和实验结果

3.1 基于Simulink与ADAMS的联合仿真

为了验证模糊PID算法的可行性，在Simulink中对起落架模糊PID控制系统进行仿真分析，并设期望距离为258.5 mm，仿真结构如图5所示。

图5 Simulink仿真结构图

图6为在各控制器下起落架足端足垫位移曲线，模糊PID控制器和PID控制器与传统的匀速变换的控制器相比，模糊PID调节曲线更加迅速，模糊PID控制器在1.97 s调整完毕，PID控制器则是在2.65 s调整完毕，相对既有的PID算法，模糊PID在调节时间上有了很好的优化。

图6 Simulink仿真位移曲线

将所得数据输入到ADAMS中建立的起落架模型中，对起落架进行分析，仿真结果如图7所示。从图7中可以看出：仿真经过2 s后起落架与地面开始接触，2.1 s时起落架受力达到最大状态之后开始反弹起落架与地面相离，2.3 s后再次接触地面，2.5 s时起落架达到稳定状态。

利用ADAMS对底座受力进行仿真，结果如图8所示。从图8中可以看出：起落架在模糊PID与PID控制下受到的最大冲击力约为1 521 N，而匀速调节所受的冲击力约为2 357 N，模糊PID调节和PID调节与常规匀速调节相比，减少了35%的冲击力，说明采用PID控制器很大程度地改善了起落架受力情况，增加了起落架使用寿命。

图7 ADAMS仿真模糊PID调节过程

图8 ADAMS仿真底座受力

3.2 基于树莓派实验

在树莓派运用python对基于模糊PID的位置闭环起落架控制系统进行编程实验，图9为起落架支腿调节过程。

对起落架足部位移情况做仿真与实验对比，得到足垫位置与目标值误差,如图10所示。从图10中可以看出：实验中足垫调节由于摩擦等因素的影响比仿真中的位移变化略小，但与ADAMS仿真变化趋势基本一致。说明基于模糊PID的位置闭环起落架控制系统能提高起落架调节效率，有效改善起落架受力情况，增加起落架使用寿命。

图9 基于模糊PID的位置闭环起落架实验

图10 足垫位置与目标值误差

4 结论

本文设计了基于位置闭环的模糊PID起落架控制系统，并利用Simulink与ADAMS进行联合仿真，最后利用树莓派进行编程实验，实验和仿真结果表明：①采用模糊PID控制器调节起落架的调节时间约为2 s左右，比现有的PID控制缩短了25%的时间；②采用模糊PID控制系统相比于常规调节模式能减少35%的冲击力。相对已有的起落架控制系统，基于位置闭环的模糊PID控制器提高了起落架调整效率，降低了足部受到的冲击力，增强了控制系统的适应能力。