基于GA-BP神经网络的装甲车辆电路板故障诊断

谢永成，李光升，魏 宁，李 刚

（陆军装甲兵学院 兵器与控制系，北京 100072）

装甲车辆电气系统的工作状态直接影响着装甲车辆整体作战性能。 当前，随着科技发达，电路板作为装甲车辆电气系统的关键组件，功能日趋多样、结构日趋复杂，随之而来，故障发生的种类也越来越多、复杂程度也越来越高，对故障诊断的要求也不断提升。 目前，对于装甲车辆电气系统的故障诊断，大多是系统级故障诊断，即使发现电路板故障，也多是以更换为主。 虽有部分学者将神经网络方法应用在电路板故障诊断中，但由于存在训练停滞现象、收敛效果较差等问题，使得基于神经网络的智能诊断方法应用在电路板故障诊断中存在着诸多问题和限制[1]。 为了克服该问题，有部分学者引入附加动量项、学习率自适应等方法对模型进行改进，取得了一定效果，但由于动量因子是固定的，学习率变化范围不大，其整体自适应能力仍然不够[2-5]。 基于此，文章探索将遗传算法与BP 神经网络进行结合，以尝试解决单一BP 网络容易陷入局部最小值、收敛效果差等问题，以期在以往神经网络诊断方法基础上[2-5]，为装甲车辆电气系统电路板故障诊断提供更好的解决方法。

1 典型BP 神经网络

BP 神经网络又称为误差反向传播神经网络，数据信息通过神经网络的输入端向输出端正向传播，而输出信息的误差沿着相反的方向传递给神经网络的权值和阀值，使其按照反馈信息调节网络结构[6]。BP 神经网络结构如图1 所示。

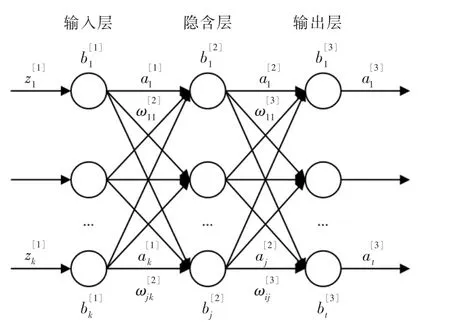
图1 BP 神经网络结构图Fig.1 BP neural network structure diagram

输出层梯度：

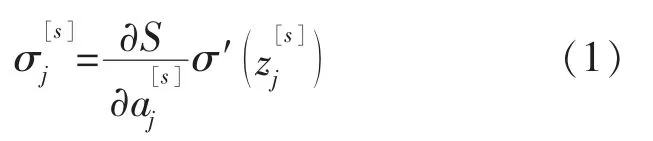
隐含层梯度：

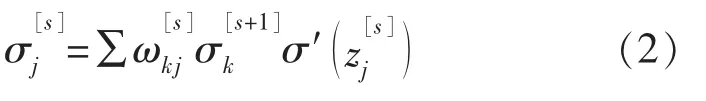
第n 次迭代阈值：

第n 次迭代权值：

学习率η 根据误差变化e（n）进行自适应调整：

由典型BP 神经网络基本结构及原理可知，虽然其具有较好的收敛速度和自适应能力，但其学习率范围和动量因子本身的问题导致其对网络误差仍然敏感性不足，难以适应学习率较大范围变化的情况。 为了解决上述问题，对其进行如下改进：

设定p1，p2分别是网络误差e（n）连续增大、减小的标志量：

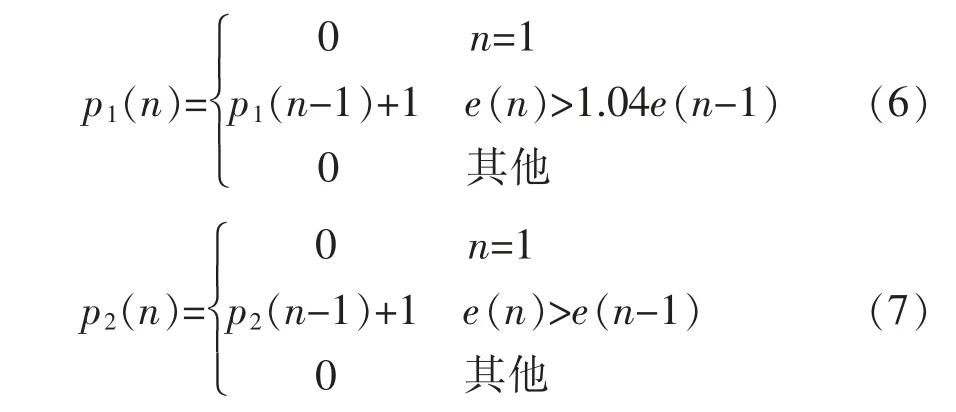
将其代入公式（5）中，得到学习率η：

自适应动量因子为

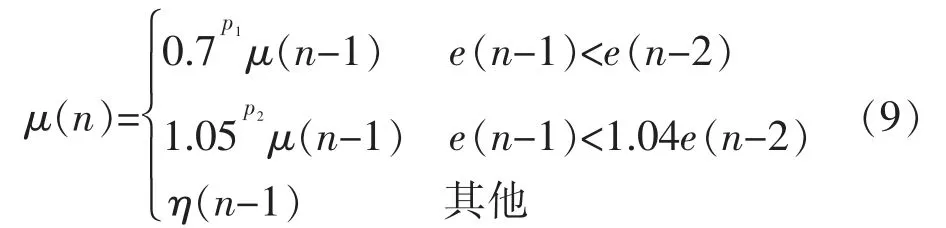
若误差连续减小k 次时， 说明方向正确但学习率不够，从而可以以k 幂指数提高η，并降低μ，推动网络进一步收敛[11]。

2 基于遗传算法的BP 神经网络参数优化方法

为了对典型BP 神经网络进行优化，可引入遗传算法， 对典型BP 神经网络的各层节点参数进行寻优操作。 遗传算法是一种常用的全局搜索方法，通过设置种群初始值、选择、交叉、变异等操作步骤，可以对典型BP 神经网络的各层节点参数进行寻优，从而降低训练停滞和局部极小值问题对模型预测结果的影响[12-15]。 其与BP 神经网络结合对各层参数进行优化的基本流程如图2 所示。

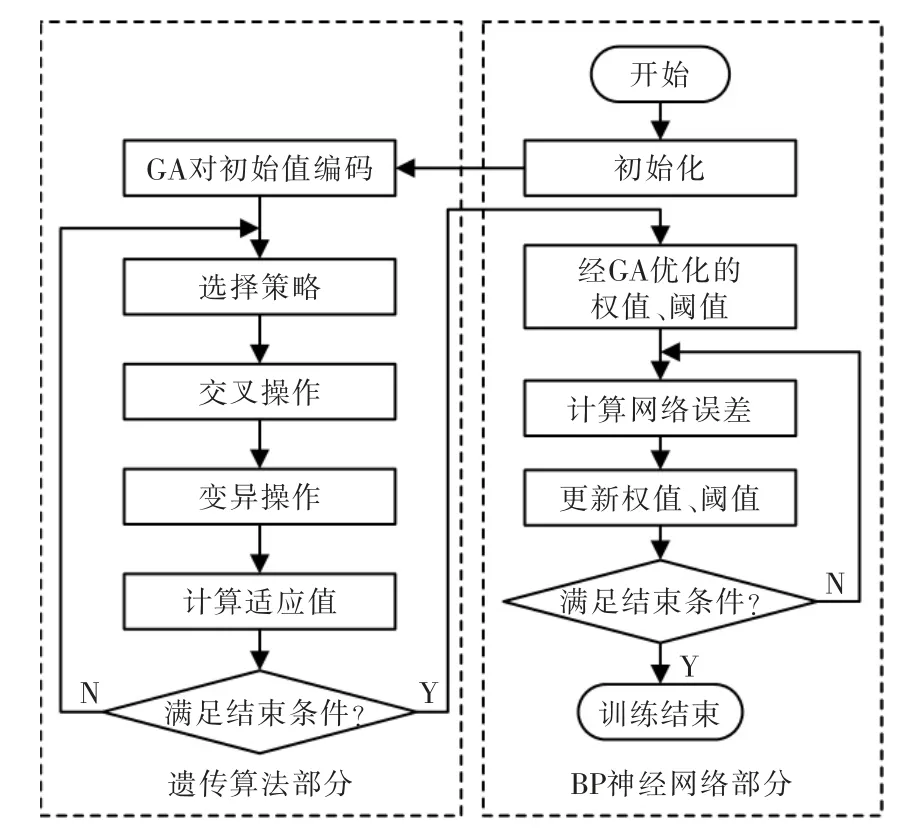
图2 改进型GA-BP 算法基本流程Fig.2 Basic flow chart of improved GA-BP algorithm

运用遗传算法对BP 神经网络模型参数寻优的基本操作可分为5 个步骤：

步骤1种群初始化。 遗传算法是从潜在的解集出发进行寻优的过程，因此，在模型运用过程中，首先应按照一定的编码规则给出种群的初始解，对种群进行初始化，生成初始种群、确定适应度函数。本模型中，选取网络误差为适应度函数。

步骤2选择操作。在本模型中，采取基于适应度比例的选择操作，每个个体被选择的几率为：Pi=

步骤3交叉操作。通过交叉操作，可以进一步增大子代基因信息范围。本模型中，第k 个染色体ak和第s 个染色体as在第j 位的交叉方法为

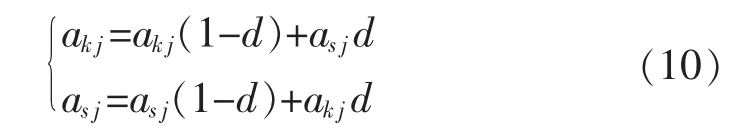
式中：d 为［0，1］之间的随机值。

步骤4变异操作。通过变异，能够提高种群的多样性，使种群得到丰富和优化。若对第i 个个体第j 个基因a 进行变异操作，可得到：

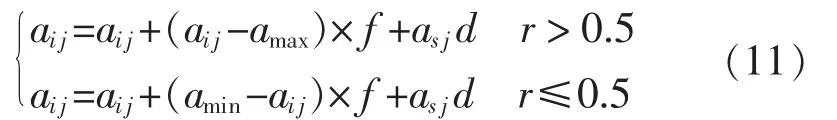
式中：amax是基因aij的上边界；为一个随机值；g 为当前迭代次数；Gmax为最大迭代次数；r 为［0，1］之间的随机值。

步骤5判断。按照上述步骤进行计算，并判断进化是否达到了预期目标，若没有达到，则重复上述步骤直到达到预设目标为止。

3 模型实现与验证

3.1 样本数据

以装甲车辆电气系统中80 式灭火系统控制盒电路板撕裂后存在故障的子网络为例，对优化后的BP 神经网络模型进行验证分析。选择撕裂后的子网络作为数据采集的区域，故障信息通过节点电压测量法获取。 其故障采集区域如图3 所示。

图3 80 式灭火系统控制盒电路板电压信息采集区域Fig.3 Type 80 fire extinguishing system control box circuit board voltage information collection area

首先设置故障元器件以及元器件所产生的故障，如表1 所示。

表1 故障注入参数设置Tab.1 Fault injection parameter settings

然后依据测量节点的顺序依次将故障测量节点命名为a～g，并将故障依次注入电路可以通过测量节点电压获得故障数据。 获得节点电压数据后，进行归一化处理，如表2 所示，对应的神经网络输出，如表3 所示。

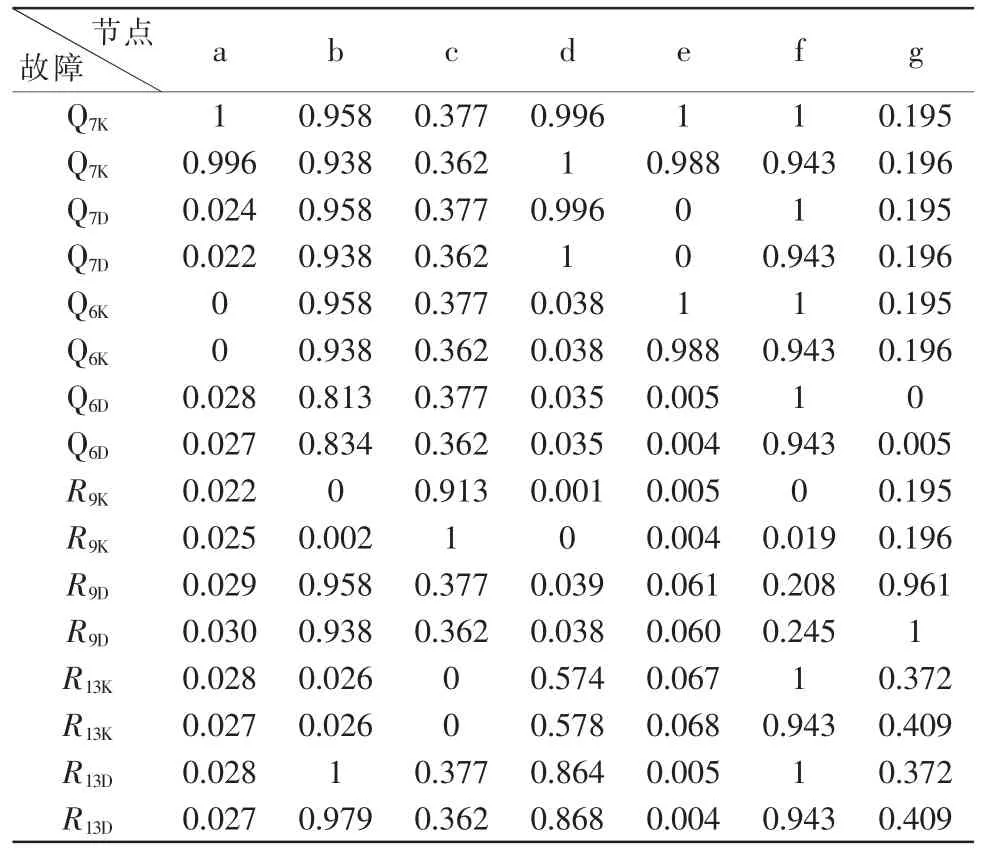
表2 故障参数（0-1）归一化Tab.2 Fault parameters（0-1） are normalized

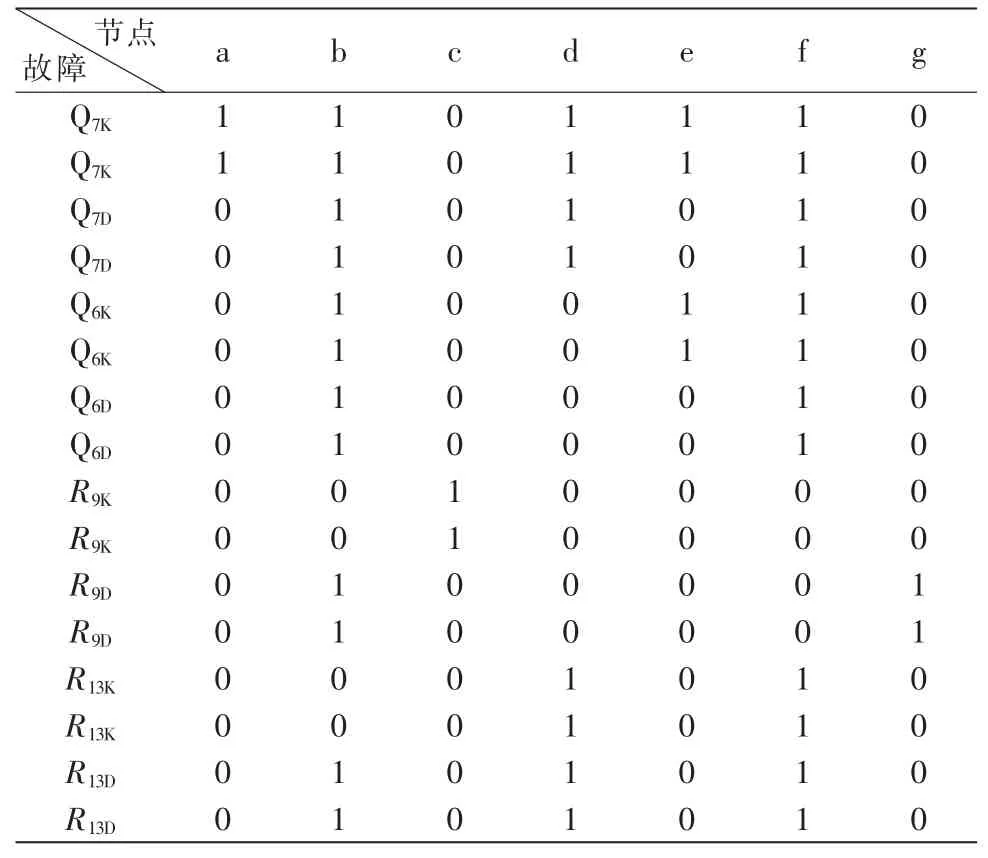
表3 故障参数（0-1）归一化网络输出Tab.3 Fault parameters（0-1） normalize the network output

3.2 模型训练及验证

设置BP 神经网络3 个层次的节点数量分别为3，5，6，η=0.8，μ=0.6，并对其进行批量训练，从而获得误差满足要求的网络模型。

对于遗传算法部分，其初始种群规模设定为16，交叉概率和变异概率分别为0.4，0.2，共进行20 次的进化，以得到经GA 优化的BP 神经网络各层节点初始值，如表4 所示。 其中，ω1～ω3是第1～2 层网络权值，b 是第2 层网络阈值，W1～W5是第2～3 层网络权值，B 是第3 层网络阈值。

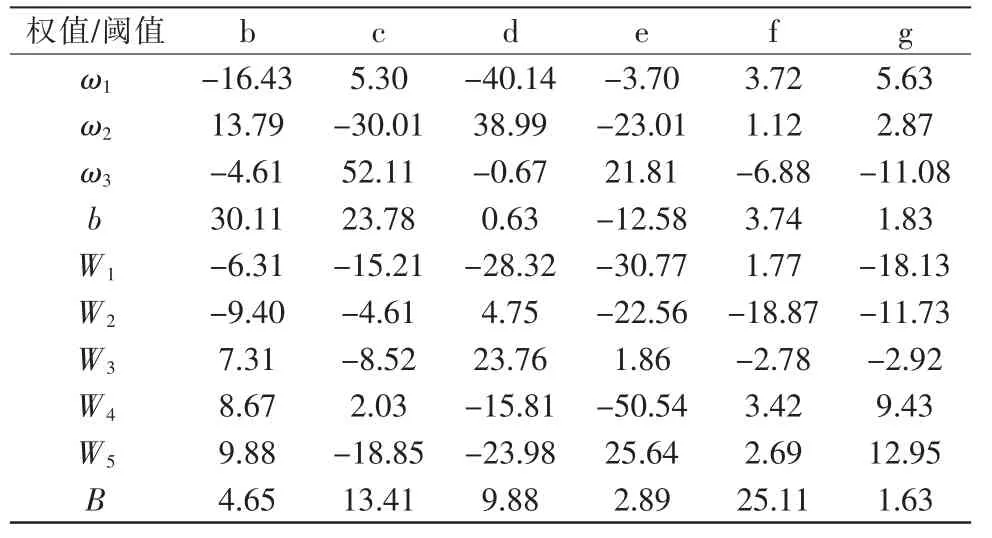
表4 优化后的BP 神经网络初始值Tab.4 Initial values of the optimized BP neural network

将上述优化得到的BP 神经网络各层节点初始值代入模型中，以表2 和表3 数据作为训练数据对模型进行训练，经过4 次迭代之后，可以得到训练误差为0.0563，此时，模型的训练误差满足要求，该模型可以对装甲车辆电气系统电路板故障进行诊断，如图4 所示。

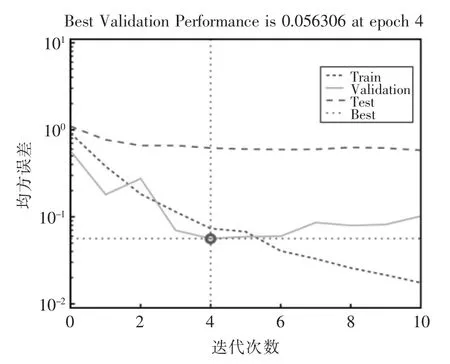
图4 优化神经网络（0，1）区间训练误差曲线Fig.4 Optimization neural network（0，1） interval training error curve

为了验证优化后的GA-BP 神经网络模型的可靠性， 将其与典型BP 神经网络以及测试数据进行预测结果对比。 首先对没有优化的典型BP 神经网络模型进行训练，经过12 次迭代之后，得到训练误差为0.16125，如图5 所示。 将实验数据分别带入优化后的神经网络模型和没有优化的神经网络模型，可以得到预测结果，如图6 所示。 可见，没有优化的网络模型预测结果明显与测试数据偏离较大，而优化后的网络模型预测结果与测试结果拟合度较好，优化后的网络模型预测结果明显优于没有优化的网络模型预测结果。

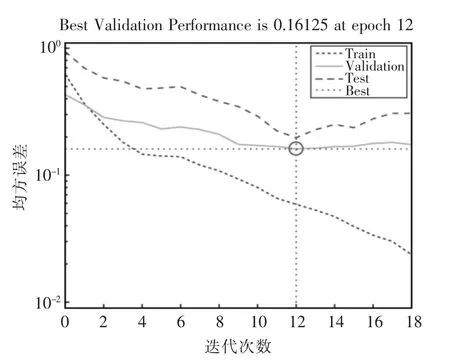
图5 未优化神经网络训练误差曲线Fig.5 Not optimized neural network training error curve

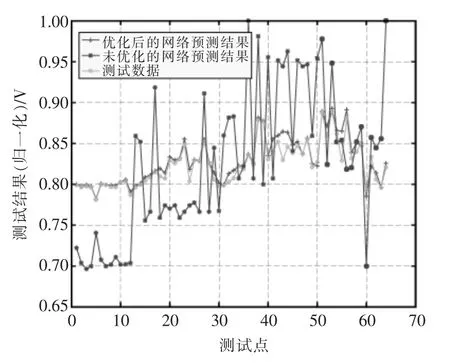
图6 免疫遗传算法预测结果对比Fig.6 Comparison of prediction results of immunogenetic algorithms

4 结语

装甲车辆电气系统电路板故障诊断问题一直是一个难点问题，传统的电路板故障诊断方法主要存在故障检出率低、虚警等问题，应用BP 神经网络虽然能一定程度上解决检出率低等问题，但其存在的自适应问题和局部极小值问题仍然导致故障诊断虚警率较高。 而通过引入遗传算法，对典型BP 神经网络进行参数寻优改进，从而使得神经网络故障诊断方法可以得到优化。 本文在改进模型的基础上， 以装甲车辆电气系统中80 式灭火系统控制盒电路板故障诊断数据对模型进行验证分析，由结果可见， 经过遗传算法参数寻优改进后的BP 神经网络模型可以有效克服自适应不够和局部极小值问题，实现对装甲车辆电气系统电路板的故障诊断。