基于GPS定位的自主运动导航系统研究

丁祖磊，蒋天泽，温秀平，曾 静

（南京工程学院 创新创业学院，南京 211167）

汽车是20 世纪最伟大的发明之一， 它让人们的出行更加的便捷和自由，使人类的生活方式发生了巨大的变化[1]。21 世纪以来，科学家和工程师们将高新电子电路、机器视觉、人工智能等学科技术应用到车辆工程上。 近几年，许多汽车制造厂商陆续推出了具有自动入库、辅助驾驶、自动泊车等功能的车辆[2]。 自主导航最开始是由谷歌在2009年公开宣布， 最早运用于汽车上， 开发自动导航汽车，国内，百度最早于2017年发布“Appllo”计划。 表面上，自动驾驶车辆是以工业量产的汽车为基础进行改装的，而本质上，是通过传感器感知外部环境，并通过计算机控制其自主运动，所以自动驾驶车辆可以归类于机器人的行列。 自动驾驶技术被国际自动机工程师学会（SAE）分为L0～L5 共计6 个等级（SAE，2014）[3]。 无人车可以分为两大类：室内无人车和室外无人车。 其中，室内无人车包括送餐机器人、扫地机器人等，室外无人车包括谷歌无人车、无人侦探车、百度无人车等；室外无人车大多以激光雷达为主，通过点云来建立周边环境的3D 模型，比如可以检测出树木、车辆、路沿、行人等细节[4]，再与GPS 定位组合，从而实现车辆所需的高精度定位[5]。 因此，室外无人车可以结合北斗或者GPS 导航系统实现室外定位，然后使用激光雷达实现车库、偏僻地区的地图构建与导航。 截至目前，已有微软、博世、大陆、TomTom、Grab 等全球近50 家企业加入Apollo平台[6]。 2019年，百度发布了Apollo 3.5 版本，它是一款可以应用于复杂的城市道路中的自动驾驶[7]，本文基于GPS 定位和高德地图，设计了一个适合于小型室外机器人本体、助盲导航等多个应用场景的导航系统。

1 系统整体框架

1.1 模块关系图

本系统主要由GPS 定位模块、 语音交互模块、路径规划模块、运动控制模块4 部分组成，如图1所示。

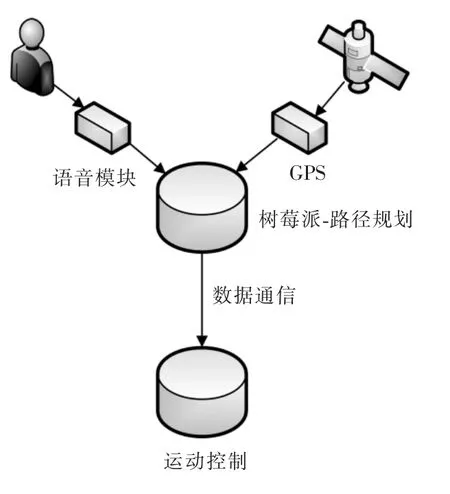
图1 模块关系图Fig.1 Module diagram

GPS 模块获取当前位置的经纬度信息，语音模块识别用户发出的指令，树莓派整合数据链接高德地图进行路径规划获取数据，将数据处理后发送至运动控制模块进行控制。

1.2 系统工作框图

在系统工作时，首先通过语音识别识别出用户想要到达的目的地，然后，对GPS 返回的数据进行解析，使用高德地图API[8]查询出当前位置和目标位置，并通过高德地图API 完成路径信息的规划，将数据发送至运动控制部分，最后对数据进行处理实现自主导航。 系统工作框图如图2 所示。

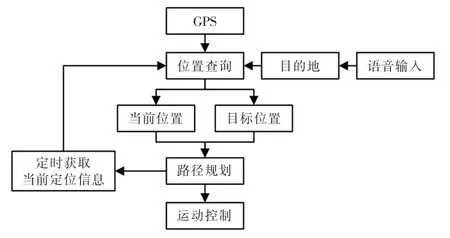
图2 系统工作框图Fig.2 System workblock diagram

2 模块设计

2.1 GPS 定位及语音识别

使用GPS 模块WTGPS+BD 实现定位， 提供初始位置， 语音识别使用百度的AI 平台对实时输入的语音进行识别，提供目的地位置。

2.2 路径规划及数据解析

本文介绍的系统在树莓派上建立上位机服务程序，将当前位置、目的地位置的经纬度作为输入参数构造出一个URL，获取服务器返回的数据对其进行解析，最后按照一定的通信协议打包发送。 运动控制获取到路径信息后，以规定通信协议进行数据解析，分别获取到所有的路径节点总数、单个路径节点数据， 在获取到所有经纬度数据后开启导航，并实时获取树莓派发送的经纬度数据，以便实现在导航时对轨迹优化的计算。

3 基于一阶多项式曲线优化的PID 控制算法

3.1 控制算法

控制算法主要包括两部分：PID 算法和一阶多项式曲线优化算法。

PID 是当下最为广泛的控制器，PID 算法具有结构简单、原理简单、参数整定的优点，并具有很好的稳定性和鲁棒性[9]。PID 调节器主要是对误差值的调节，误差值在一定程度上反映了当前位置与目标位置的一个相对距离，通过对误差值的修正，进而得到不同轮子的转速，达到修正，本系统使用的位置式PID，如公式（1）所示：

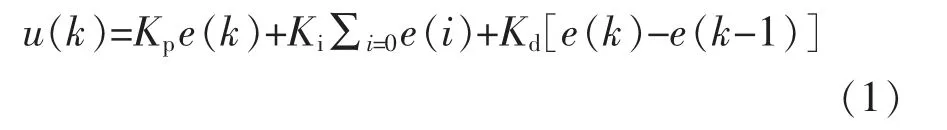
首先获取出的误差值e（k），对误差值比例放大，即乘以Kp，再计算微分量，即当前的误差值减去上一次的误差值：e（k）-e（k-1），最后再添加积分量，积分量应该在系统接近稳定时消除稳态误差，对误差累加积分，消除系统的稳态误差。

但实际使用过程中，会出现积分项过大导致系统输出错误，所以为防止积分项过大导致输出出现过调，加入了积分限幅[10]参数，对于PID 调节器来说，其工作过程是一个不断修正、矫正的环节，如果不断地积分，就很有可能导致积分饱和，输出的结果过大使对象无法执行，甚至出错，加入限幅可以有效地使系统更加稳定。

如图3 所示，其中PID 输入量、误差值可以由一阶多项式曲线得出。

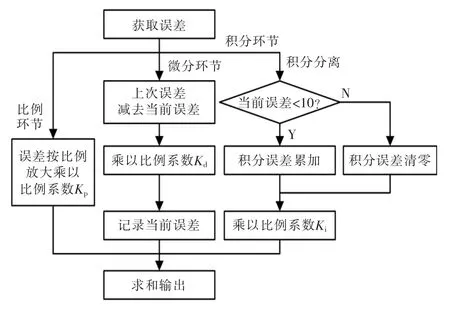
图3 PID 算法框图Fig.3 PID algorithm block diagram

在控制模块析出树莓派发送的定位数据后，使用一阶多项式曲线实现模型车在节点与节点之间运行轨迹的偏差优化。 具体采用静坐标系作为参考，模型车在此坐标系下进行运动。

在运动过程中，偏差值通过节点分段与实时位置误差计算来获取。 假设路径Route 中共有n 个节点，其中N0为起点，Nn为终点，相邻两节点做路程分段处理，设段位值P（paragraphs）初始为1，表示介于N0与N1之间，即Pn表示Nn-1Nn段，为最后一段路程，在P=1 时，当到达节点N1，则P=P+1，进入下一段路程，直至P=n 时，当到达节点Nn表示结束，并到达终点。

根据每段起点与终点的经纬度即可求出对应的直线方程，如公式（2）所示：

式中：y=Latitude（纬度）；x=Longitude（经度）。

另外还需考虑模型车在静坐标系下修正方向与运动方向的关系，如图2 所示，用A1～A8八个点构成一个静坐标系下的环形轨迹，B 点作为误差点，其中A1，A2纵坐标相同，A3，A4横坐标相同，A5，A6纵坐标相同，A7，A8横坐标相同。 轨迹上A1点沿着顺时针方向在轨迹上进行运动， 则依次经过线段A1A2（k=0），A2A3（k<0），A3A4（k=∞），A4A5（k>0），A5A6（k=0），A6A7（k<0），A7A8（k=∞），A8A1（k>0），其中轨迹中对角位置运动方向相反，因此在静坐标系下左右修正方向亦相反。 因此需考虑不同斜率下不同运动方向的偏差计算与修正。 静坐标系下修正方向与运动方向关系如图4 所示。

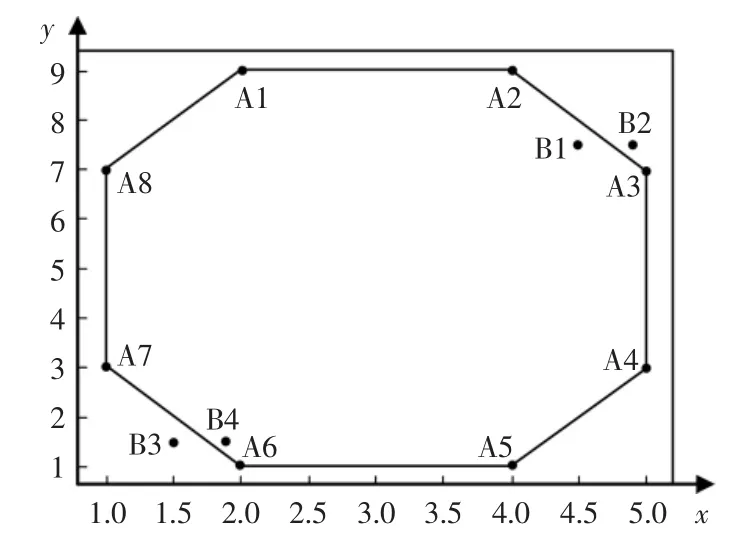
图4 静坐标系下修正方向与运动方向关系示意图Fig.4 Relationship between corrected direction and motion direction in static coordinate system

设实时经度为Xnow，纬度为Ynow，终点经度为Xfinish，纬度为Yfinish，运动方向为dir，dir 计算方法如公式（3）所示：

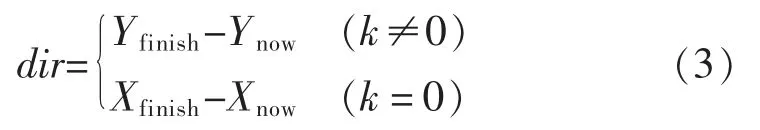
当dir>0 表示正方向运动，即包括A6A7，A7A8，A8A1，A1A2段；

当dir<0 表示负方向运动，即包括A2A3，A3A4，A4A5，A5A6段。

当运动轨迹出现偏差，运动到如图4 中B1点所示位置，需将其进行修正至A2A3线段上，其斜率kA2A3<0，dirA2A3<0，因此在静坐标系下按照其运动方向应当向左进行修正，并且修正偏差值ErrorB1可通过公式（4）进行计算：

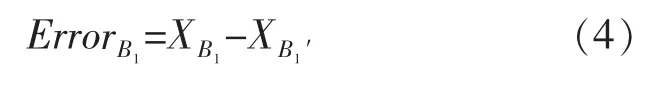
式中：XB1为B1点经度值；XB1′为B1点以纬度作为标定，带入公式（2）计算得到的线上经度值，如公式（5）所示：

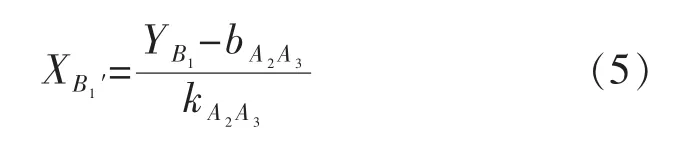
将公式（5）代入公式（4）即可得到B1点在线段A2A3上的实际偏差值ErrorB1<0，采用同样的方法可得到B2点实际偏差值ErrorB2>0。

即得到转向修正公式（6）：

相对于同斜率反方向运行的A6A7段，其斜率kA6A7<0，dirA6A7>0，其附近B3偏差点而言需要向右进行修正，为满足公式（6）条件，因此B3点实际偏差值可由公式（7）计算可知ErrorB3>0。

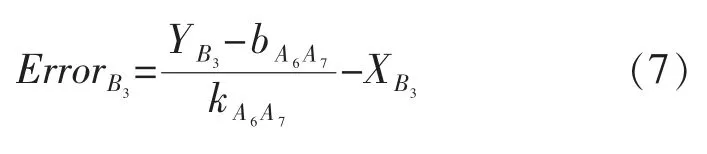
同理可知k>0 与k=∞在此静坐标系下方向修正与运动方向情况与k<0 相同，但在k=∞时经度值处处相等，因此计算XB′满足公式（8）：

综上所述，在k≠0 时，其误差计算方法如公式（9）所示：

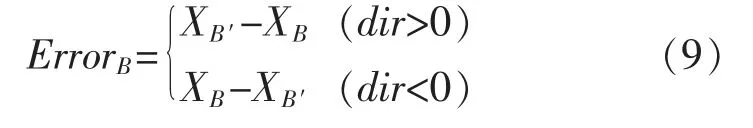
式中：XB为k≠0 时误差点的经度值；XB′为线上修正值，XB′计算如公式（10）所示：

在k=0时纬度值处处相等，因此YB′=Yfinish，其误差计算方法如公式（11）所示：

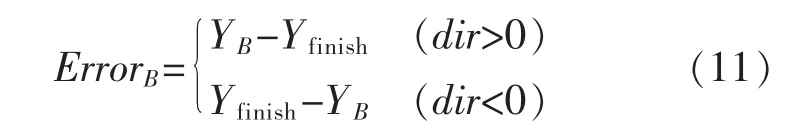
式中：YB为k=0 时误差点的纬度值。

根据上述式（9）～式（11）可计算出图2 所示的任意一偏差点对应所示线段的偏差值ErrorB， 由公式（6）可知，偏差值ErrorB即反应了电机转数，因此将偏差值进行PID 调节后转换成电机转数送至电机控制函数即可实现模型转向控制。

3.2 运动控制算法验证

根据分析得出的计算公式计算出其偏差值与对应直线方程的k，b 进行输出。 并将偏差值送至PID调节器进行输出控制模型车转向进行测试，在实际测试过程中以南京工程学院（2 号门）到南京工程学院工程实践中心4 号楼为例进行自主导航，其部分测试数据如图5 和图6 所示。 图5 为规划好的路径图，图6 中阴影为轨迹运行点，折线段为路径，模型能够通过GPS 返回的数据进行误差判断并进行自主调节，因此该运动控制算法验证通过。

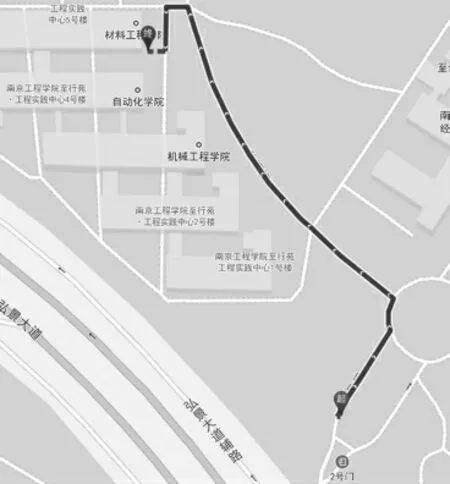
图5 轨迹图Fig.5 Trajectory diagram

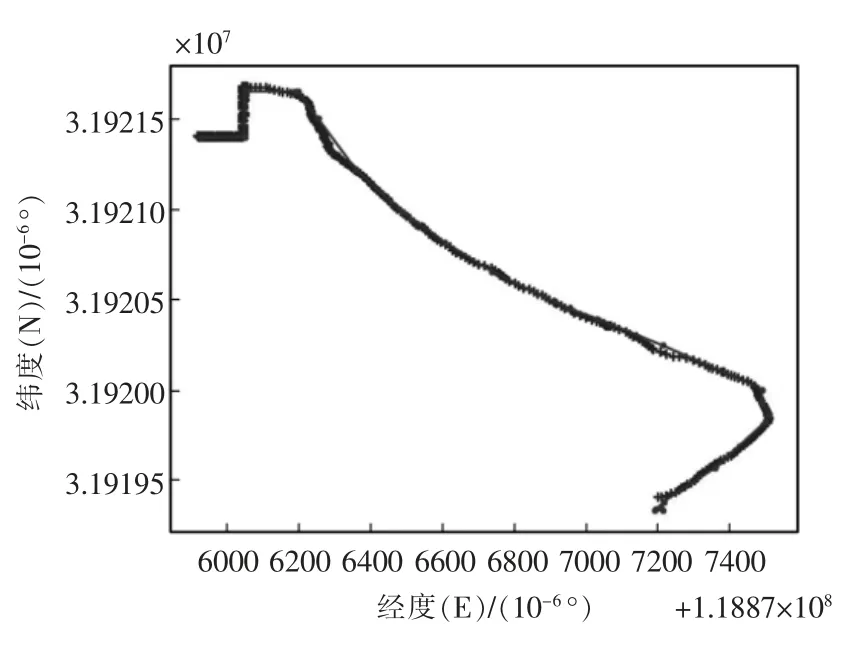
图6 轨迹验证图Fig.6 Trajectory verification diagram

4 结语

本文主要介绍了自主导航控制系统的研究和设计，主要对路径数据获取、数据接收与处理进行了系统设计与介绍。 并对轨迹优化算法进行了论证与说明，通过理论分析与公式推导，对静态坐标系下一阶多项式曲线轨迹优化算法的运动轨迹误差值进行分析，最后通过模型实验验证，并得出结论。