虚拟直流电机惯性阻尼自适应控制策略

徐 敏，赵巧娥

（山西大学 电力与建筑学院，太原 030013）

落实碳达峰、碳中和目标，构建以新能源为主体的新型电力系统是时代赋予的责任和使命，电力系统正形成高比例电力电子设备、低转动惯量特性[1]。 积极开展虚拟电机技术改造应用，对于提升系统稳定运行将至关重要[2]。

虚拟直流电机控制（VDCM）使变换器具备惯性阻尼特性[3]。 文献[4-6]均在阻尼系数和惯性系数固定的VDCM 基础上进行理论分析及仿真验证，只考虑惯性阻尼支撑， 未考虑系统对动态响应的要求；文献[7]中阻尼系数、惯性系数自适应函数分段太多且不连续；文献[8]引入调节参数和阈值，增加可调变量；文献[9]将阻尼系数、惯性系数对应阻尼比、超调量等绘制在一张图中， 可根据需求确定公共区，从而确定两系数范围，计算复杂。

本文在传统虚拟直流电机控制基础上，提出一种惯性系数和阻尼系数自适应策略。 该自适应函数仅分两段且变化连续，在抵抗扰动和恢复稳态时提供不同的惯性和阻尼，减小电压波动时间。 最后，通过Simulink 仿真对所提控制策略和其他自适应策略进行仿真对比，验证其有效性。

1 虚拟直流电机控制

双向DC/DC 变换器VDCM 控制框图如图1 所示，在电压电流双闭环中加入VDCM。 电压环不仅根据参考值Uref调节母线电压Udc，且产生系统功率需求参考；VDCM 部分利用直流电机电枢回路方程和机械方程，使变换器具备惯性和阻尼。 VDCM 环节输出电枢电流ia，不考虑变换器功率损耗，通过功率守恒得到蓄电池侧电流参考值ibat*。 通过PI 调节得到占空比d 以及触发信号，最终使储能及其变换器输出特性等效为直流电机，如图2 所示。

图1 双向DC/DC 变换器VDCM 控制框图Fig.1 Bidirectional DC/DC converter VDCM control block diagram

图2 VDCM 等效模型Fig.2 VDCM equivalent model

直流电机电枢回路方程为

式中：U 和Ea为机端电压和感应电动势；Ra和Ia为电枢电阻和电枢电流；CT为转矩系数；φ 为磁通；ω 为直流电机转速。

直流电机机械方程为

式中：J 为惯性系数；Tm为机械转矩；Te为电磁转矩；D 为阻尼系数；ω 和ωn为实际角速度和角速度参考值。

2 惯性阻尼自适应

2.1 小信号分析

在稳态工作点处添加扰动，结合图2 整理后可得DC/DC 变换器传递函数Gud和Gid为

式中：L 为蓄电池侧滤波电感；C 为母线侧电容。

结合图1 以及式（1）～式（5），可得整个控制闭环传递函数为

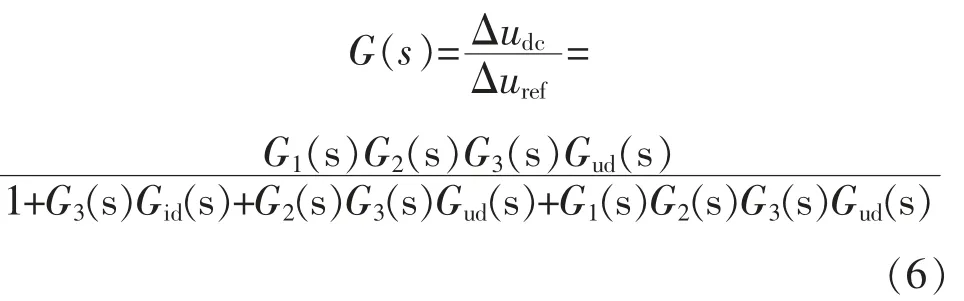
其中：

式 中：kpu，kiu为电压环PI参数；kpi，kii为电流环PI参数；Uref为电压参考值；Vm为载波峰值。

根据闭环传递函数，在MATLAB 中绘制惯性系数J 从2～8 的单位脉冲响应。 J 变化时的单位脉冲响应如图3 所示，可以看出，J 越小，电压超调量越大，恢复速度越快。 J 参数根轨迹如图4 所示，当J<0.461 时，根轨迹在右半平面，系统不稳定。 因此，电压处于稳态时选择较大J 抵抗扰动， 减小电压波动幅值；恢复时选择较小J 加快恢复速度，且J 应大于0.461。

图3 J 变化时的单位脉冲响应Fig.3 Unit impulse response when J changes

图4 J 参数根轨迹Fig.4 Root locus of the J parameter

阻尼系数D 从2.5～10 的单位脉冲响应如图5 所示。D 越大，恢复速度越快。单位阶跃响应如图6 所示，D 越大，稳态误差越大；D 取10 时，输出稳态值已经降到给定值的80%。 因此，D 在稳态时选取较小值，且不超过10；在恢复时可以选取较大值，来加快恢复速度。

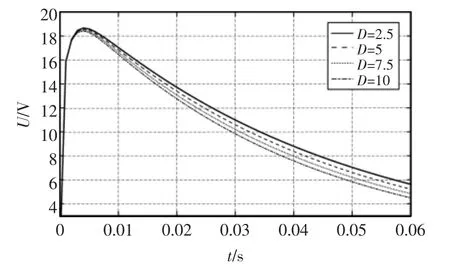
图5 D 变化时的单位脉冲响应Fig.5 Unit impulse response when D changes

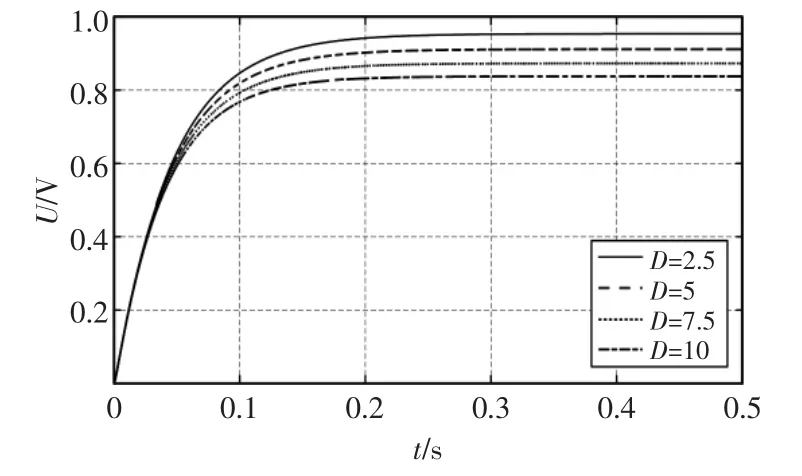
图6 D 变化时单位阶跃响应Fig.6 Unit step response when D changes

2.2 自适应控制策略

以负载突减为例，电压波动如图7 所示。 根据电压偏差变化趋势，提出一种自适应控制策略：

图7 受到扰动后电压动态变化Fig.7 Dynamic changes of disturbed voltage

1）区间1 电压偏差增大，因其时间短，J 和D 选择较大固定值，提供惯性和阻尼支撑。 并避免不必要的系数变动增加控制复杂度甚至影响电压稳定。

2）区间2 电压偏差减小，J 采取较小值，D 选取较大值，使母线电压快速恢复至稳态。

3）恢复至稳态后，J 和D 回到固定值为下一次功率波动做准备。

满足上述条件的函数为

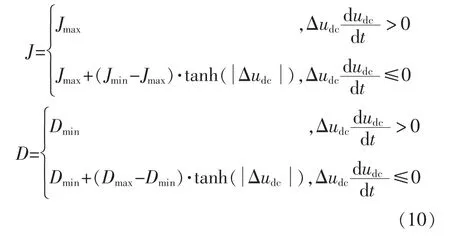
3 仿真验证

在MATLAB/Simulink 中，搭建直流微网模型如图8 所示。光伏侧变换器以最大功率输出，储能侧变换器采用虚拟直流电机控制，仿真参数如表1 所示。

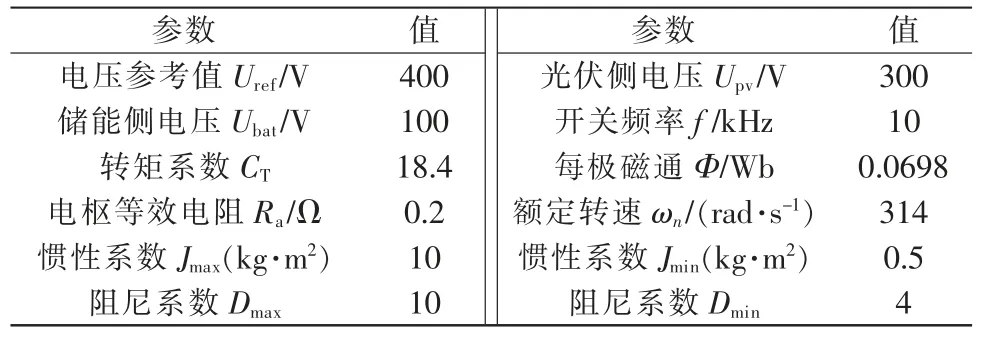
表1 仿真参数Tab.1 Simulation parameters

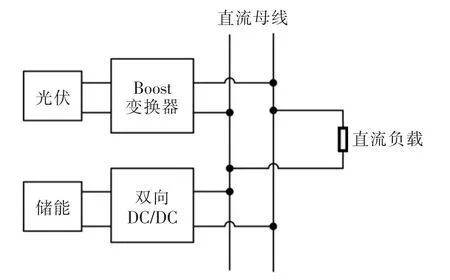
图8 直流微网模型Fig.8 DC microgrid model

负载功率如图9 所示，负载功率在0.3 s 时由25 kW 突减至10 kW，0.5 s 时突增至45 kW。储能变换器采用J，D 固定和自适应VDCM 对应直流母线电压波形如图10 所示，采用J，D 自适应控制时电压恢复至稳态速度更快。 对比文献[7-8]中自适应VDCM，直流母线电压波形如图11 所示。 J，D 采用文献[7]中自适应函数时，电压波动幅值和稳态误差较大且恢复速度慢；采用文献[8]中自适应函数时，初始阶段出现电压尖峰，负载功率变化小时，电压平滑且接近给定值，但在0.5 s 负载功率波动大时电压开始振荡， 阈值的设定可能会使电压不稳定，且增加控制复杂度。 本文所提自适应策略电压恢复时间短，且能承受较大功率波动。

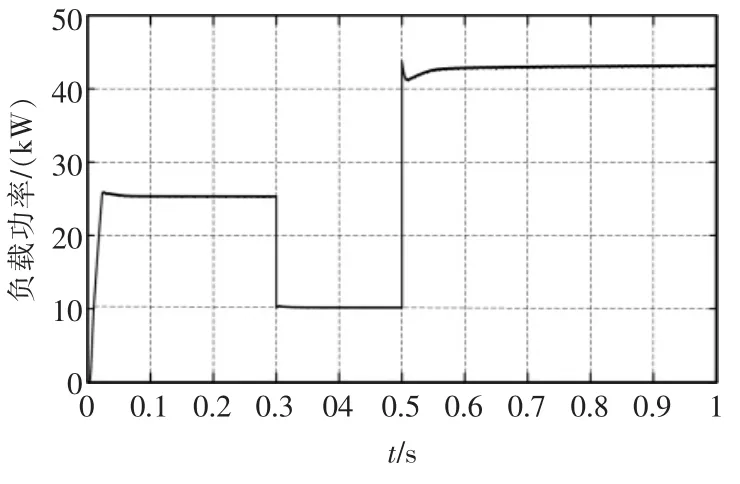
图9 负载功率Fig.9 Load power

图10 J，D 固定和自适应的VDCM 控制效果对比Fig.10 Comparison of the control effect of fixed and adaptive J，D of VDCM

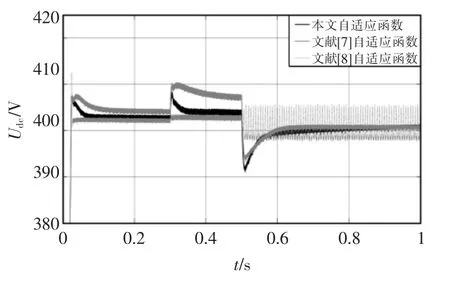
图11 本文与文献[7]和文献[8]自适应函数控制效果对比Fig.11 Comparison of the control effect of adaptive function proposed in literature[7] and literature[8] and this paper

4 结语

针对固定参数VDCM 控制动态响应和阻尼惯性支撑的矛盾，提出一种J，D 自适应VDCM 控制策略。该自适应函数简单，不确定参数少。通过与固定参数和其他自适应VDCM 进行仿真对比，可得在母线电压超调量基本不变的情况下，恢复至稳态的时间明显缩短。 研究表明所提自适应策略可通过动态调节惯性和阻尼系数，使系统在具备惯性和阻尼支撑的同时具备良好的动态性能。