基于扰动估计器的永磁同步电机滑模控制

王乐园，王树波

（1.青岛大学 自动化学院，青岛 266071；2.山东省工业控制技术重点实验室，青岛 266071）

近年来，永磁同步电机（permanent magnet synchronous motor，PMSM）因其功率密度高、效率高等特点，被广泛应用于数控机床、航天等领域。 但传统比例积分微分控制器（proportional integral differential controller，PID）策略因其抗扰与内部摄动能力较差，已不能适用于多变量、强耦合的复杂机电的PMSM 系统中。

针对传统PID 存在的问题，提出了一些非线性控制方法如自抗扰控制、预测控制、滑模控制[1-5]。 在众多控制策略中，滑模控制因其具有很强的鲁棒性的特点以及对系统参数要求低等诸多优点被越来越多的学者关注，并应用到伺服系统中。 传统滑模控制通过增大增益来提高响应速度，无可避免的带来抖振问题和收敛速度慢问题。 文献[6]改进了传统滑模指数趋近律，引入双曲正切设计一种新型边界层饱和函数，提高系统响应速度的同时削弱系统的抖振。 文献[7]为了改善DC–DC 功率变换器的性能，设计了基于UDE 的滑模控制方法，为了解决不匹配的不确定性，构造自适应滑模函数，对估计的不确定性进行补偿，从而可以得到无抖振的鲁棒控制律。 文献[8]提出基于滑模的变速直驱风能转换系统方案，改良了滑模技术的趋近律，减少抖振并改善了总谐波失真的特性，从而可知滑模策略在变速直驱风能转换系统等复杂非线性系统控制中表现出良好的性能。 不确定性干扰势必会影响电机控制系统，其影响包括外界环境干扰和电机控制系统内部参数变化造成的干扰影响。 不确定性扰动估计器（uncertainty and disturbance estimator，UDE） 采用滤波器对扰动进行估计已应用到机械臂、四旋翼无人机及桥式吊车系统等控制中的扰动估计，相比时延观测器，UDE 扰动估计效果比较好。 文献[9]基于UDE 的原理，运用内膜原理解决设计滤波器和参考系统的问题，实现渐进参考跟踪和干扰抑制，保证闭环系统的稳定性。文献[10]提出了一种基于UDE的模型参考自适应滑模控制策略，确定了桥式吊机可以在不确定性条件，达到预期位移的同时少量抵消负载摆动。

本文提出采用一阶模型不确定与扰动估计器的滑模调速控制相结合的控制策略，将一阶模型不确定与扰动估计器与滑模控制相结合，使用一阶模型不确定与扰动估计器对未知扰动进行了估计、补偿，提高了控制器抗干扰能力，引入一种基于双曲正切函数的变速趋近律，在滑模变量收敛过程提高增益值，在进入稳态时降低增益值，提高滑模变量暂态收敛速率和降低控制器抖振。

1 永磁同步电机数学模型及干扰估计器设计

1.1 永磁同步电机数学模型

PMSM 在d-q 轴的数学模型为

式中：ud，uq分别为d，q 轴电压；id，iq分别为d，q 轴电流；Ld，Lq分别为d，q 轴电感；R 为定子电阻；ωm为电机转动时的机械角速度。

在d-q 轴参考坐标系中，PMSM 的电磁转矩方程为

PMSM 运动方程为

式中：J 表示永磁同步电机的惯性转矩；B 表示摩擦系数；P 表示极对数；ωm表示电机转动时的机械角速度。

电角速度可以表示为

1.2 永磁同步电机矢量模型

定义扰动为

当id=0 时，的大小决定了电磁转矩的大小。

1.3 不确定干扰估计器设计

建立PMSM 控制模型，将总扰动定义为d，利用UDE 对干扰进行估计，同时在速度环中设计滑模跟踪控制器，对扰动进行精确观察，并将扰动前馈补偿。

将总扰动带入永磁同步电机转速状态方程里，可表示为

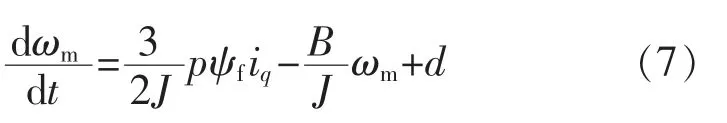
根据不确定性干扰估计器（UDE）算法[11]可知：当干扰通过适当带宽的低通滤波器时，可以抑制高频扰动，并对低频扰动进行估计。 采用具有适当频率特性的滤波器来估计干扰：

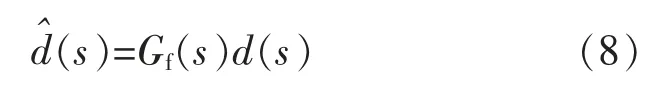
即：

式中：Gf（s）=，τ 表示低通滤波器的带宽。

2 滑模控制器设计

2.1 新型趋近律

传统指数趋近律如下所示：

针对传统趋近律收敛速度慢、 抖振大的问题，本文提出一种新型趋近律：

其中：

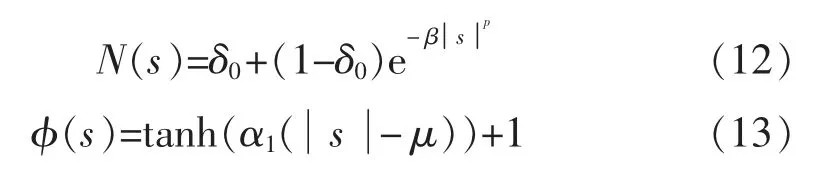
式中：k1＞0；k2＞0；0＜σ＜1；0＜δ0＜1；β＞0；p＞0；α1＞0；0＜μ＜1。

为了验证φ（s）函数可有效改善收敛速度，φ（s）函数的曲线图如1 所示。

仿真对比式（10）和式（11），可得如图2、图3 所示。 由图2、图3 分析可知，在远离滑模面时，变速趋近律的收敛速度远大于传统趋近律，且在靠近滑模面时抖振抑制性能优于传统趋近律，在速度和位置跟踪，也强于传统趋近律，所以新型趋近律的性能更优越。

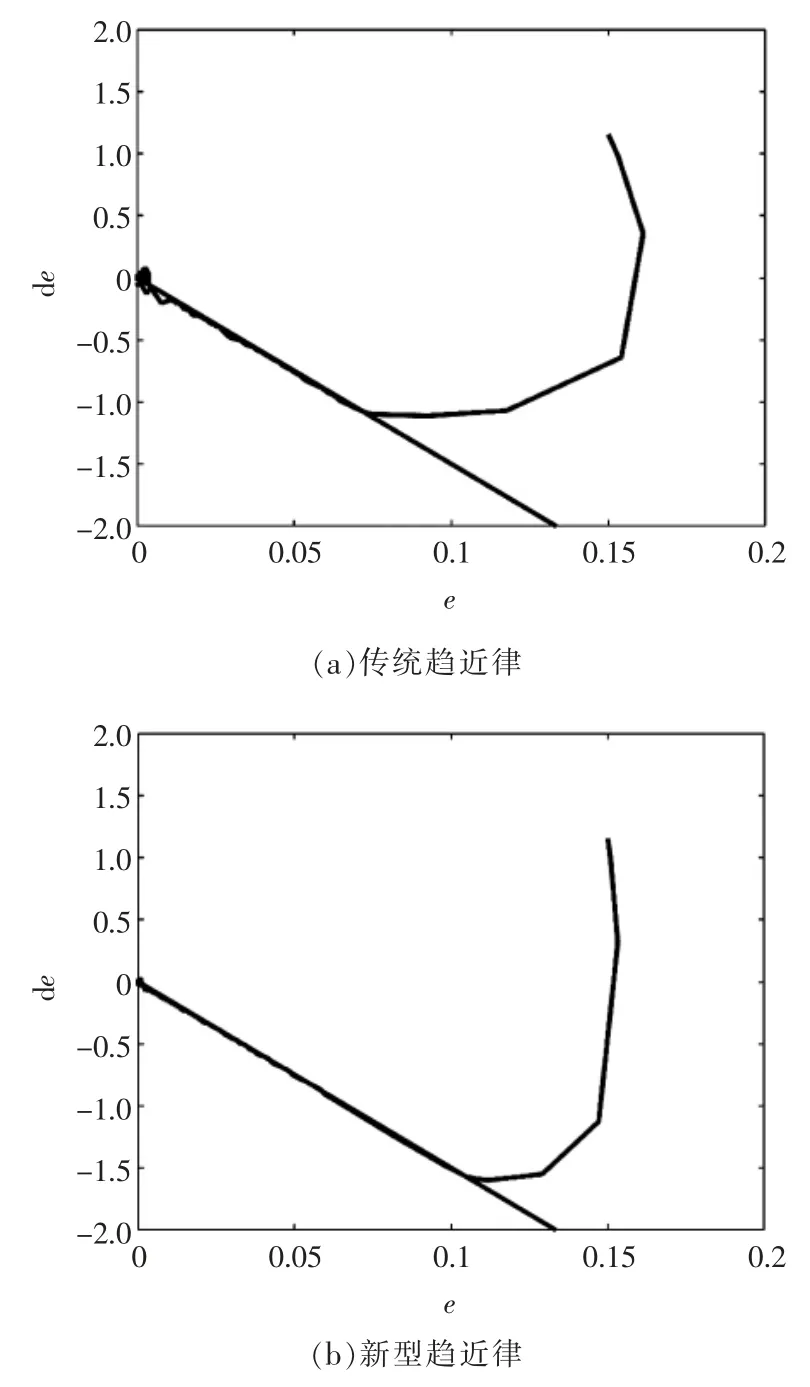
图2 相轨迹Fig.2 Phase trajectory

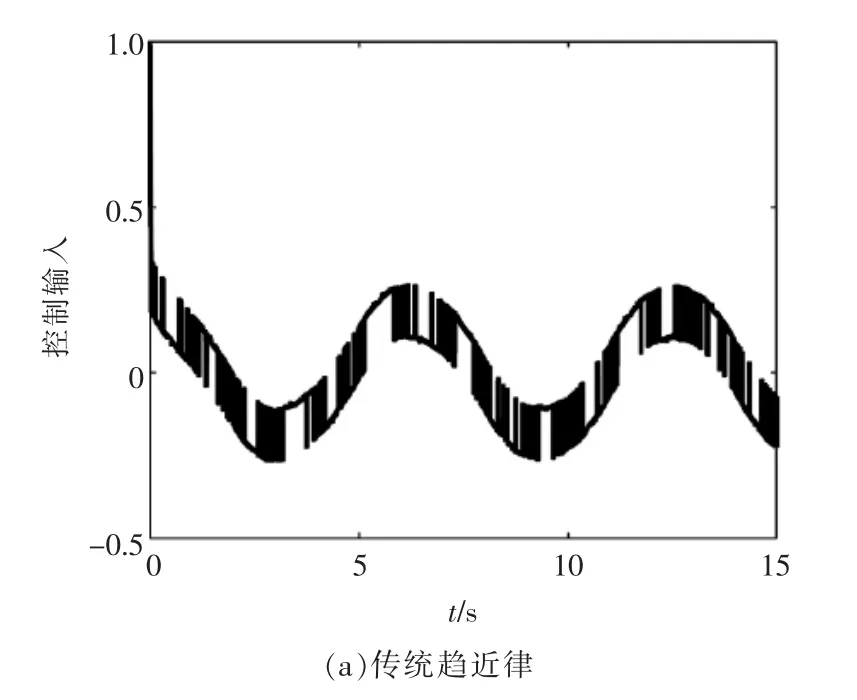
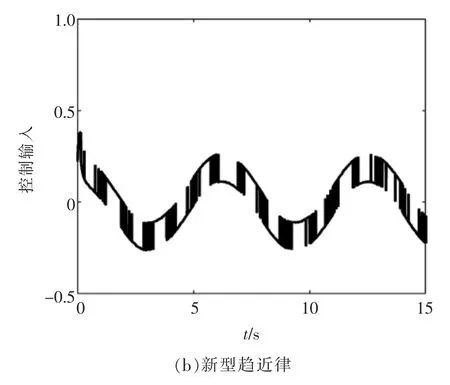
图3 控制输入Fig.3 Control input

2.2 滑模控制器设计

定义速度环跟踪误差：

通过选取积分型滑模面能够有效平滑转矩，并降低抖振，提高系统的鲁棒性，从而在一定程度上改善调节精度[12]。 故设计滑模面为

式中：c 为滑模面的积分系数。

对s 求导，得：

式（3）代入式（2）可得：

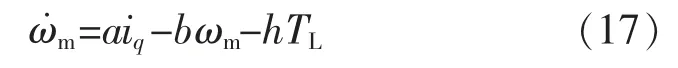
考虑系统扰动，可将上式等价为

结合式（11）、式（16）及式（17）等，得：

将式（19）代入式（7）可得：

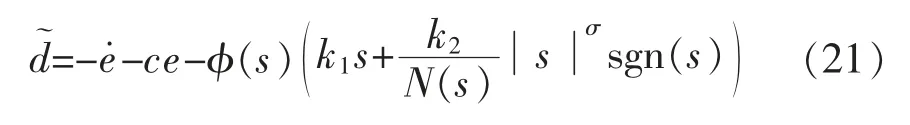
式（21）表示干扰估计误差，c 决定状态轨迹误差的收敛性。当干扰相对恒定时，d～的值将接近于0，那么控制器将获得相对良好的转速跟踪效果。

3 稳定性分析

定义李雅普诺夫函数：

对V 求导可得：

结合式（16）、式（18）可得：

上式可表示为

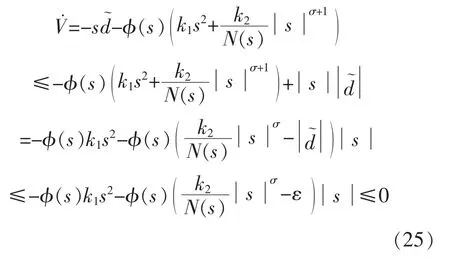
式中：ε 为极小值。 由图1 可知φ（s）≥0，且N（s）＞0，显然≤0，满足条件，所设计的控制器稳定。

图1 φ（s）函数曲线图Fig.1 Function graph of φ（s）

4 仿真分析

为了分析验证此控制策略的作用效果，对设计的基于UDE 的永磁同步电机滑模控制器进行仿真验证，控制仿真框图如图4 所示。

图4 基于干扰估计器的滑模控制系统仿真框架图Fig.4 Simulation frame diagram of sliding mode control system based on disturbance estimator

永磁同步电机参数如表1 所示。

表1 永磁同步电机参数Tab.1 Parameters of permanent magnet synchronous motor

选取PMSM 粘滞摩擦系数B=0.008，给定d=sin（t）和对设计的控制器各项参数进行调节，运用工程经验法对PID 进行参数整定，再以滑模控制器下系统输出为参考，调节PID 控制器和传统滑模控制器各项参数。

控制器参数α1＝100，k1＝13，k2＝13，β＝10，σ＝0.5，p=10，δ0=0.5，μ＝0.1，c=3 扰动观测器参数τ＝0.01。PID 控制器参数kp=10，ki=0.05，kd=0.005。 传统滑模控制器的参数ε＝0.01，k=24。 分别给予参考速度和外加扰动正弦信号、阶跃信号，仿真结果如图5～图12 所示。

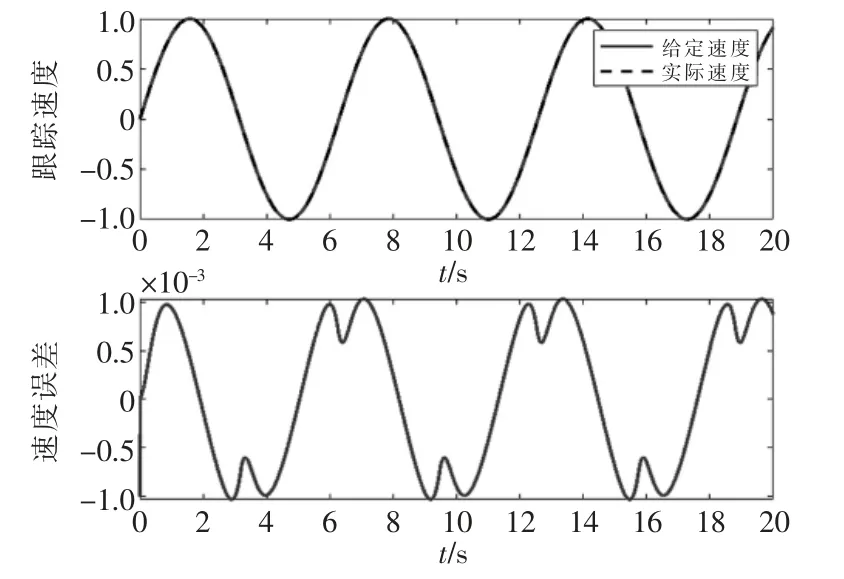
图5 正弦信号的速度、速度误差图Fig.5 Velocity and velocity error diagram of sinusoidal signal

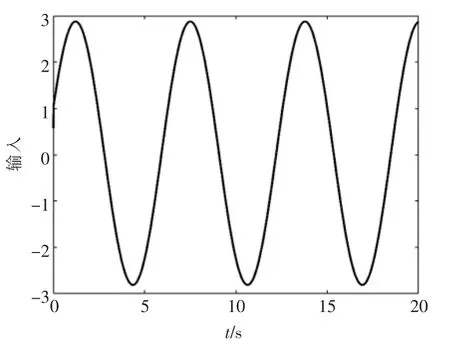
图6 正弦信号的控制输入Fig.6 Control input of sinusoidal signal

图7 正弦信号的扰动估计、估计误差Fig.7 Disturbance estimation and estimation error of sinusoidal signal

图8 速度、速度误差对比图Fig.8 Comparison diagram of speed and speed error

图9 阶跃信号的速度、速度误差图Fig.9 Velocity and velocity error diagram of step signal

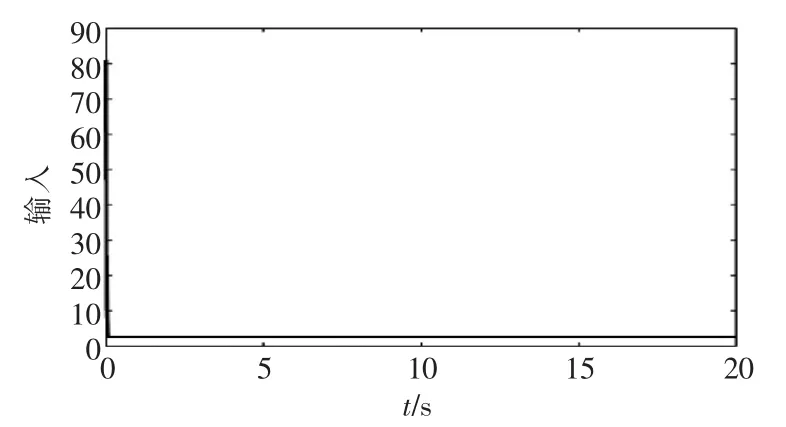
图10 阶跃信号的控制输入Fig.10 Control input of step signal

图11 阶跃信号的扰动估计、估计误差Fig.11 Disturbance estimation and estimation error of step signal

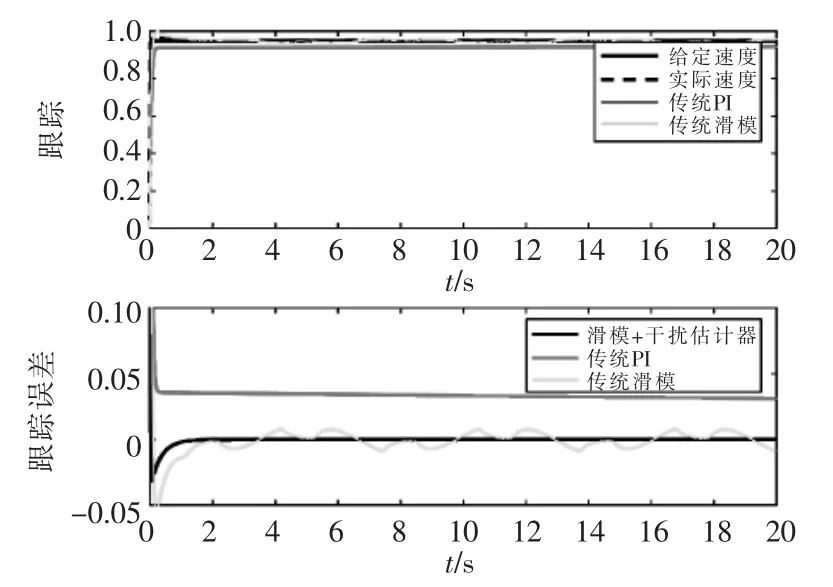
图12 速度、速度误差对比图Fig.12 Comparison diagram of speed and speed error

经过仿真对比得出，在干扰状态下，传统PI 和传统滑模在调控永磁同步电机速度时， 超调量较大，响应反应时间长且速度较缓慢，基于UDE 的滑模控制调速方法在调控永磁电机转速时，超调量较小，响应时间短且速度较稳定、准确，通过适当频率的的滤波器，估计和补偿系统的干扰，使其具有较好的鲁棒性和灵敏度，同时还具有较强的追踪能力。

5 结语

为了取代传统的PI 控制和传统的滑模控制，在传统滑模控制的基础上，设计了具有变速趋近律的滑模控制策略，应用到永磁同步电机调速中，使系统跟踪效果和稳定性变得更好，并针对扰动设计了一种不确定扰动估计器，较准确的估计和补偿了未知扰动，增强了系统的对干扰的适应性。 仿真结果证明，该算法有效改善了PMSM 调速系统的动态性能，提高其对扰动的适应性。