循环扰动荷载作用下花岗岩损伤及破裂特性研究

陈文昭,蒋一凡,刘夕奇

(1.南华大学 土木工程学院,湖南 衡阳 421001;2.武汉大学 土木建筑工程学院,湖北 武汉 430000)

0 引 言

随着各国浅层矿产资源的开采殆尽，岩、矿采掘作业逐渐深入深部地下空间。深部岩石相较于浅部岩石而言，往往处于“三高一扰”的复杂力学环境中，在该环境下极易引发深埋隧洞围岩产生高能级、大体量的岩爆、冲击地压等工程灾害，甚至可能导致采场失稳坍塌，对施工人员及设备安全构成严重威胁[1-2]。因此，合理地对岩石进行扰动荷载作用下的研究，对于防止地下工程灾害事故的发生具有重要意义。

近年来，诸多岩石领域学者对岩石在动静组合加载下的力学特性进行了大量的研究，从而对揭示深部岩体的岩爆成灾机制具有一定的意义。如，杨福见等[3]基于对岩体开挖后岩体内部应力重分布的理解，提出了一种研究深部岩石在扰动荷载作用下力学特性的新方法；S.Ghasemi等[4]对辉长岩试样进行单调和循环加载试验，研究了辉长岩中微裂纹在静、动荷载作用下的演化规律，结果表明，循环加载的试样比单调加载的试样更早出现微裂纹扩展，且除加载至峰值强度的试样外，循环加载的试样微裂纹长度较高；刘德克等[5]利用有限元软件FLAC3D探究了岩石在动静组合加载的不同单轴轴压作用下的岩石的强度变化、破坏特征及应力应变等力学特性进行了分析；T.Xu等[6]通过砂岩样品进行了一系列常规单轴压缩试验和循环加载试验，得到了最大应力和应力幅值与单轴抗压强度的比值是影响砂岩疲劳寿命的最重要因素，数值砂岩试样最大应力和/或应力幅值越大，疲劳寿命越短；杨鹏等[7]通过对大理岩、矽卡岩和蛇纹岩三种岩石开展不同应力扰动幅值下的力学试验，提出了应力上限门槛值的概念，认为循环扰动加载下应力只要不大于上限门槛值，岩样就不会发生破坏。此外，还有诸多学者从蠕变特性、声发射特征、红外热像、能量耗散等[8-14]角度对循环荷载作用下岩石的力学特性、损伤及破裂等方面进行了研究。

以上学者的研究虽然取得了丰富的成果，但大多数的研究在于研究岩石在循环荷载作用下的变形特征以及岩石在不同应力水平、应力幅值条件下的力学特性，而对岩石在高应力条件下的循环扰动试验还研究较少。因此，本文以四川省双江口水电站深部隧洞采集的岩样为研究对象，对其进行了室内动静组合加载下的单轴压缩试验，揭示循环扰动荷载对岩石的影响规律，从而为隧道工程施工及岩爆预警提供理论依据。

1 试样制备及方案

1.1 试验设备及试样制备

本次试验采用的仪器为中国科学院武汉岩土研究所研制的RMT系列电液伺服试验机(如图1所示)。该力学试验系统可以实现频率在0～20 Hz之间、荷载大小在0～500 kN之间的轴向循环扰动荷载，精确地测量试样在单轴条件下的力学特征。

图1 试验设备

本文研究的试样为取自四川省双江口水电站的花岗岩，岩体完整且材质较硬，无明显节理，主要由石英、黑云母等矿物质组成。采用水刀切割方法，将一整块岩石切割成30个50 mm×100 mm的试验标准圆柱体试样。采用图1设备对岩样进行单轴压缩试验，得到岩样的静力学参数如表1所示，单轴压缩应力-应变曲线如图2所示。

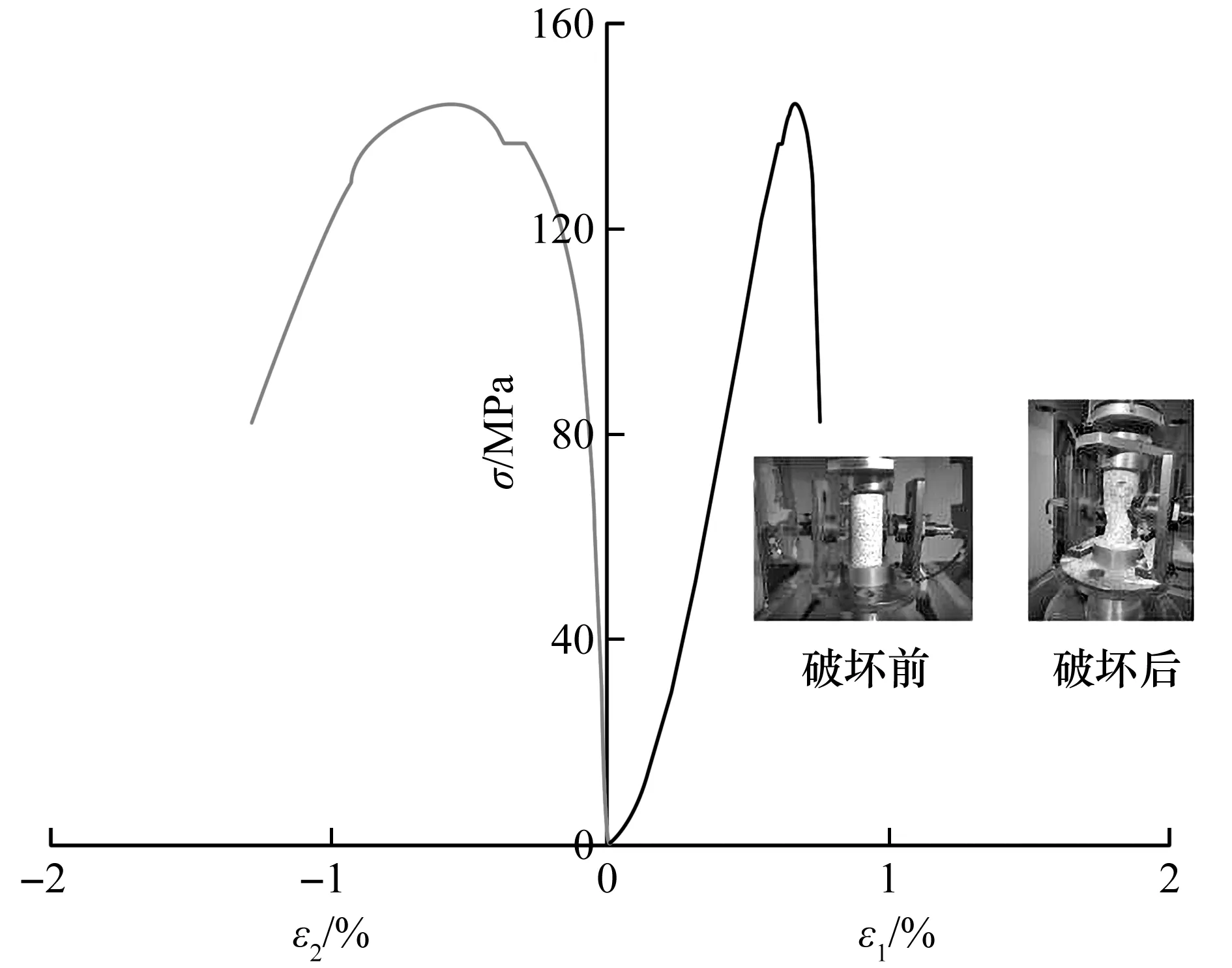
图2 单轴压缩应力-应变曲线

表1 岩石静力学参数

1.2 试验方案

试验采用单轴动静组合加载方式，具体加载过程如图3所示，先采用斜坡控制力的方式对岩样缓慢施加轴向静荷载，加载至一定数值σm后施加波形为正弦波的循环扰动荷载，图中T为一个循环加载周期，扰动荷载上限记作σmax，下限记作σmin，扰动幅值Δσ=σmax-σmin。

图3 循环扰动荷载加载过程示意图

具体加载方案如表2所示，首先对岩样以5 kN/s的速率施加轴向静载，加载至单轴抗压强度的60%、70%和80%后，再施加扰动荷载，扰动荷载的幅值为20 MPa、30 MPa和40 MPa，试验直至岩样破坏为止。

表2 循环动力扰动力学试验方案

2 试件破坏分析

2.1 破碎岩块筛分

对破碎后的岩石采用0.05～45 mm的标准筛进行筛分试验，将碎屑粒径分为0.05～1 mm、1～5 mm、5～10 mm、10～15 mm、15～20 mm、20～25 mm、25～30 mm、30～35 mm、35～40 mm、40～45 mm十个等级，并称量各筛孔上剩余碎屑的质量，将其转换成各筛孔孔径下岩石碎屑的筛下累计百分含量，得到花岗岩在不同扰动幅值下的碎屑颗粒级配曲线，如图4所示。

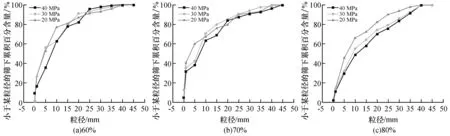
图4 不同扰动幅值下的颗粒级配曲线

工程上常用级配曲线的不均匀系数Cu和曲率系数Cc量化粒径分布的均匀程度和连续性程度，从而判断级配优劣[15]。其中：

(1)

(2)

式中：d10，d30，d60分别表示小于某粒径的质量占总质量的10%，30%，60%所对应的粒径。

由图4中的级配曲线可以得到的相应的特征粒径，从而计算出不同工况下的碎屑的不均匀系数和曲率系数，如表3所示。

表3 颗粒级配不均匀系数及曲率系数

当曲率系数3≥Cc≥1时，碎屑颗粒的分布是连续的，由表3的计算结果可以看出，静载加至单轴抗压强度的60%时，不同应力扰动幅值对应的曲率系数Cc分别为4.45、3.82、3.22，说明岩样碎屑分布是不连续的；而静载加至单轴抗压强度的70%和80%后，在不同应力幅值作用下的碎屑曲率系数均大于1且小于3，说明连续。当不均匀系数Cu≥5时，碎屑的粒径分布是不均匀的，且Cu越大碎屑的均匀性越差[16]。也即，曲线越平缓，碎屑粒径的变化范围越大。从表3的计算结果可以看出，虽然不均匀系数都大于5，但却呈现减小的趋势，说明随着初始静载及扰动应力幅值的增大，岩样碎屑的分布越趋于均匀。

由上述岩样碎屑粒径分析并结合宏观破坏现象观察可以得出，不同应力扰动幅值加载下，岩样碎屑分布有明显不同。当扰动应力幅值较小时，岩样碎屑破碎程度较低，碎屑粒度差较大，分布不均匀，且连续性较差，主要分布为较大的片状碎屑；而在较大的应力扰动幅值加载下，模型岩样破碎程度较高，碎屑粒度分布较均匀，连续性相对较好。

2.2 分形维数的计算

根据N.E.Odling等[17]学者建立的岩石碎屑粒径分布的分形模型，分形维数F可以通过筛分试验的质量-频率关系求得。岩石在循环扰动荷载作用下产生的碎屑分布方程为：

(3)

上式两边同时取对数，得:

(4)

式中：MT、M(x)为碎屑的总质量和筛下累计质量；xm、x为最大碎屑粒径和粒径；F为分形维数。

图5、图6、图7是对初始时施加不同静载σm的lg(M(x)/MT)-lgx散点图进行线性拟合的直线，拟合直线的斜率为(3-F)，进而可以求出分形维数F。由图5～图7可知，花岗岩破碎碎屑筛下累计质量的百分含量与筛孔尺寸在双对数坐标系中呈现良好的线性相关关系，说明可以用分形维数定量表征岩石试件的破碎程度。

图5 60%的lg(M(x)/MT)-lg x曲线

图6 70%的lg(M(x)/MT)-lg x曲线

图7 80%的lg(M(x)/MT)-lg x曲线

2.3 分形维数与扰动幅值的关系

根据上述lg(M(x)/MT)-lgx曲线中拟合直线的斜率，求得不同工况下各岩样的分形维数F如表4所示。由表可知，相关系数R2均处于较高水平，说明岩石在循环扰动荷载加载下的碎屑粒径分布满足分形规律。当试件具有相同轴向静应力σm时，分形维数F随着扰动幅值的增大而增大，最大分形维数达到2.4左右。由于可以用分形维数表征岩石的破碎程度，则可总结出：F值越大，岩石破碎的程度越高。

表4 花岗岩碎屑参数统计

3 扰动荷载下模型损伤分析

岩石破坏的过程在某种意义上也可以定义为损伤累积的过程，当损伤变量达到一定值时，岩石发生破裂。根据岩石在单轴压缩条件下的损伤本构方程[7]:

σ=εE(1-D)

(5)

由于在循环扰动荷载作用下，扰动幅值Δσ保持不变，因此，可将式(5)中的σ由Δσ代替，便得到循环扰动荷载作用下损伤变量D与应变之间的关系式：

(6)

对式(6)两边同时进行求导，得：

(7)

对式(7)两边同时积分，得：

(8)

(9)

式中：ε0为循环扰动开始时得纵向应变；ε为试样破坏时的纵向应变；C1、C2为积分常数。当D=0时，ε0=ε，代入式(9)，得C1=C2。当D=1时，试样破坏，假设εd为试样破坏时的纵向应变，将ε=εd代入式(9)，得：

(10)

将式(10)和C1=C2代入式(9)，得:

(11)

图8为岩石在轴向静载加至试验设计的单轴抗压强度后，不同扰动幅值下循环次数与损伤变量的关系曲线。从图8中可以看出，损伤变量在循环扰动作用下，呈现出快速增大-平稳增长-快速增长的变化趋势，且随着扰动幅值的增大，平稳增长过程中循环次数显著减小。

将平稳增长区段损伤变量的变化率定义为V，计算公式如下：

(12)

式中：Db、Da为平稳区段起始损伤变量；Cb、Ca为平稳区段起始扰动荷载已循环的次数。

表5为运用式(12)计算出各岩样平稳区段损伤变化率结果。由表5可知，扰动荷载的幅值和初始时施加的轴向静载的大小都对损伤变化率有很大的影响，当初始静载较小时，即初始静载加至抗压强度的60%，70%时，对应的3种扰动幅值下的损伤变化率差值在0.2范围内，损伤变量变化率随扰动幅值的增加的变化速率较慢；当初始施加的轴向静载为单轴抗压强度的80%后，3种扰动幅值下的变化率为0.89、1.34、5.5，损伤变量的变化率随着扰动幅值的增加而显著提高。扰动幅值为40 MPa时，3种不同初始静载下的变化率分别为0.76、0.81、5.5，说明不同的初始静载对损伤的变化率也有一定的影响。

4 结 论

1)随着岩样加载扰动应力幅值的增大，岩样碎屑的分布越趋于均匀。初始静载加至单轴抗压强度的60%时，不同扰动幅值下岩石的碎屑分布是不连续的，碎屑破坏程度较低；当初始静载加至大于单轴抗压强度70%以上时，岩石的碎屑分布是连续的，且破碎程度较高。

2)分形维数F可以用来定量评价岩石的破碎特性。岩石在扰动荷载作用下的破碎粒径分布符合分形规律，且随着初始时施加的轴向静载σm和扰动幅值Δσ的增大，分形维数F越大，岩石破碎程度越深，表现出良好的线性相关关系。

3)扰动荷载作用下，损伤变量呈增大-平稳-增大的变化趋势，且扰动幅值Δσ的大小对岩石平稳区段的循环次数和损伤变化速率存在显著影响。