基于数值模拟的露天矿高陡边坡可靠度分析

尹 归,陶干强,朱忠华*,孙海帝

(1.南华大学 资源与环境安全工程学院,湖南 衡阳 421001;2.湖南柿竹园有色金属有限公司,湖南 郴州 423037)

0 引 言

随着我国露天开采逐步向深部发展，高陡边坡稳定性问题愈发严重，其稳定性已成为露天矿安全生产的关键技术问题之一[1]，也是边坡处治措施及安全评价的研究热点。数学分析方法是目前学界与工程界进行边坡稳定性评价的常用方法，曹兰柱等[2]、韩万东等[3]分别采用Morgenstern-Price极限平衡法以及Spencer条分法和Bishop条分法对边坡破坏机制和稳定性状况进行了计算分析。但由于岩土体是一种具有非连续性、非均质性的复杂材料，岩土体力学特性离散性较为显著，且受限于技术水平，所获取的力学参数具有较大的不确定性。这使得采用确定力学参数的常规数学分析方法的计算结果的可靠性与准确性受到影响，而概率分析方法的引入，则为该问题的解决提供了新途径。蒋水华等[4]应用随机响应面法对边坡系统展开了可靠度分析；唐小松等[5]则利用Bootstrap抽样技术对边坡可靠度展开研究；彭兴等[6]基于蒙特卡洛模拟实验理论，为边坡可靠性分析提供了方法和框架。随着研究逐步进展，边坡稳定性分析已经有了大量研究成果，计算体系也逐渐完整，但目前对边坡展开研究时，常局限于采用单一的方法进行研究，若将两种或多种分析方法综合起来对边坡稳定性进行分析，会更加有效。

边坡稳定性分析是分析边坡稳定程度及合理确定边坡参数的重要方法，为边坡处治和安全评价提供依据[7]。目前，边坡稳定性分析常用的方法有极限平衡分析方法、数值分析方法和可靠度分析方法。这些分析方法由于需要特定的假设条件，都具有一定的局限性。数值模拟方法能够得到边坡最可能的滑动面和相应的安全系数，但没有统一的边坡失稳判据，不能判断边坡是否失稳，无法得到边坡的破坏概率；可靠度分析方法将边坡部分参数视为随机变量，用概率论方法分析边坡稳定性，可以得到边坡破坏概率，但是计算过程需多次假定滑动面，才能找出其最可能的滑动面，耗时较长。因此，本文将可靠度理论与数值模拟方法相结合进行边坡稳定性研究，并以某露天矿高陡边坡为算例，验证该方法的可行性。首先，根据露天矿边坡的工程地质特征，确定边坡模型的材料属性及材料的物理属性，并以工程实际尺寸，使用三维数字矿山软件建立边坡三维表面模型，再利用C++编程实现限定Delaunay四面体网格剖分。剖分结束后，将剖分的网格数据转化为后缀为flac3d或f3grid的计算模型，通过命令impgrid载入FLAC3D[8]，采用强度折减法模拟计算得到最有可能的滑动面和相应的安全系数；最后用验算点法对其最有可能的滑动面进行可靠度计算，确定可靠性指标和破坏概率。

1 边坡数值模拟

1.1 四面体网格剖分

网格剖分是有限元分析前处理的关键技术，四面体网格相比于六面体网格而言，具有更好的几何适应性，而且灵活性好、结构简单、自动化程度高。对模型进行剖分时，只要生成的四面体数量足够多，就能无限接近于模型边界，能够很好地模拟复杂的地质体，不容易引起应力集中，且计算模拟的精度有所提高。因此四面体网格在三维空间得到广泛应用，是当今网格生成领域的研究热点。Delaunay四面体网格剖分是目前最为流行的剖分方法之一。

限定Delaunay四面体剖分就是把一个带边界约束三维区域空间划分成一个四面体网格，对三维模型进行限定Delaunay四面体剖分，先将模型划分为若干个限定线段和限定平面，而且在最后生成的四面体网格中这些限定线段和限定平面必须存在；并将限定的线段和平面分别分成小线段和小三角形，再对这些小线段和小三角形的顶点组成的点集进行Delaunay四面体剖分，限定Delaunay四面体则就是由这个点集的顶点构成[9]。

一般情况下，顶点集中的任意两点在三维区域都可见，若两点之间存在约束面，且两点连线与该面的夹角不为0，则认为两顶点不可见，可见性受到约束面片的阻挡。如图1所示，点p和点q是区域中的两个顶点，位于面片f的两侧，他们的连线与f相交，p、q不可见。

图1 限定Delaunay四面体规则示意图

一个限定Delaunay四面体的四个顶点都是相互可见的，其外接球不包含除四面体顶点外的其他顶点。如图1所示，点a、b、c、p构成四面体是限定Delaunay四面体。

本文采用C++语言编写四面体剖分程序，剖分算法数据结构主要包括点、面和四面体数据结构。点数据结构主要记录剖分后生成的数据点的数量和各个数据点的三维坐标；面数据结构主要记录输入模型的边界面个数和边界面的顶点信息，以及四面体剖分后生成三角面个数和每个三角面顶点信息；四面体结构记录剖分后的四面体信息，包括生成的四面体个数和每个四面体的4个顶点的信息。算法首先生成包含整个输入模型的大四面体，然后对模型限定边界进行离散，将每条限定边分成若干个线段的集合，在限定边离散的基础上对限定面进行平面域上的三角化，生成所有的限定点集(包括限定点，限定线段的端点和三角网格的顶点)的Delaunay四面体网格，使其满足平面的限定条件。然后对限定边和限定面进行恢复，如果某条线段在四面体集合中没有出现，则加入该线段中点细分，直到受限边出现在剖分结果中，若在限定面上生成的三角形被干涉，则将该三角形的外心点加入到四面体网格中，从而达到恢复受限边和面的目的。最后判断生成的网格所有四面体单元是否满足Delaunay外接球准则，若不满足，则对网格进行优化调整，使其满足Delaunay外接球准则。

1.2 强度折减法基本原理

强度折减法将边坡的安全系数定义为使边坡刚好达到临界破坏状态时，对其强度参数进行折减的程度[10]。是将确定的边坡原始黏结力C和内摩擦角φ的正切值同时除以折减系数K[11-14]：

(1)

通过不断试算折减系数K，最后得到使边坡产生破坏时的折减系数K就是边坡的安全系数。强度折减法采用二分法迭代计算折减系数，使用二分法迭代折减系数就是不断将折减系数下限值Kmin和上限值Kmax之间的范围缩小到前一次迭代时的一半，当折减系数上限值Kmax与下限值Kmin小于给定计算精度η时，停止计算。根据上述折减系数二分迭代算法，折减系数迭代次数Imin可用式(2)表示：

(2)

式中：Kmax、Kmin分别为折减系数上限值和下限值；η为给定误差。

2 可靠度计算方法

边坡可靠性分析方法是以定值安全系数法为基础，根据极限平衡原理建立状态方程，用以计算边坡可靠度概率的分析方法[15]。可靠指标法包括中心点法和验算点法，但中心点法存在难以对随机变量实际分布加以考虑等缺点[16-17]，故采用验算点法进行计算。

影响边坡稳定因素有很多，如降雨、地震或爆破作用、边坡岩体性质、是否存在结构面以及结构面大小等，这些不确定的变量就是随机变量，在边坡可靠性计算中用于构建描述边坡状态的函数模型：

Z=g(X)=g(X1,X2,…,Xn)

(3)

当功能函数式(3)比较复杂时，为近似求解功能函数的均值与方差，求解结构可靠度指标，需引入标准化变量，若Xi为某一变量的特定值，对应的标准化变量xi为：

(4)

其中μXi和σXi分别为Xi的均值和标准差。

标准化变量的平均值点是标准空间中的坐标原点。因此边坡的状态方程可表示为：

Z=g(x)=g(x1,x2,…,xn)

(5)

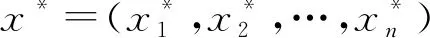
(6)

Z的均值和标准差为：

(7)

(8)

则对于所有i值，用标准化变量表示解为：

x*=-αiβ

(9)

从原点到x*的距离即是可靠指标。即：

(10)

由于验算点和β皆为未知，需用迭代法计算，采用Fiessler迭代计算步骤如下：

1)建立状态方程Z=g(x)；

2)导出g(x)的表达式；

4)令x=0，β=0；

6)计算g(x)；

7)由下式算出Z的标准差：

(11)

8)用下式计算新的x值：

(12)

9)按式(10)计算β值；

重复步骤5)到9)直到数值收敛到允许误差内为止。

迭代计算收敛后，得到可靠性指标β，进而求得边坡破坏概率。

3 工程应用

3.1 地质特征

本文研究的露天边坡位于云南省易门铜厂，该露天矿属于高原山区地形，中间被铜厂沟切割，海拔2 180～2 375 m，地形总体是中间低，两边高，地形坡度一般为15°～35°之间。矿体走向长1 600 m，延伸大于300 m，矿体倾角在42°～45°之间，属于倾斜矿体。境内山峦重叠，地质环境薄弱，边坡稳定性较差。边坡位于该露天矿东南侧，边坡设计台阶高度为15 m，台阶坡面角为65°，总体边坡高度为330 m，边坡角度为45°。经钻孔揭露，构成边坡体的主要岩石有泥质白云岩、灰白色白云岩、青灰色白云岩、火成胶结角砾岩等。边坡所处位置地质大致分为4个岩层，第一层至第四层分别为火成胶结角砾岩、青灰色白云岩、灰白色白云岩和泥质白云岩，岩石节理裂隙不发育，水文地质条件简单，地表水系不发育，地下水埋藏较深，因此本文未考虑地下水作用。

3.2 数值模拟

考虑到计算机计算能力和内存大小的限制，建立块段模型时，由于泥质白云岩、灰白色白云岩、青灰色白云岩三种岩性力学参数十分相似，可合并成一种岩性。当边坡台阶数目较多时，采用FLAC3D对边坡进行稳定性计算时，会出现单个台阶破坏或台阶联合破坏，对边坡整体破坏产生一定的影响，在研究边坡的稳定性时，本论文侧重于研究边坡的整体破坏，为避免台阶破坏对计算造成一定影响，将边坡面转化为平面，不考虑台阶的影响。计算中使用的力学参数如表1所示。另外，为配合数值计算的需要，需考虑边坡岩体稳定影响范围和数值模拟软件计算能力，根据地层确定的数值计算范围见表2。依据数值计算范围构建边坡三维模型，进行限定Delaunay四面体剖分，将剖分结果导入到FLAC3D中，得到的数值模拟分析模型如图2所示，模型朝采场方向的为白云岩组岩性模型，其余部分为火成胶结角砾岩组。另外，为便于计算结果对比，使用FLAC3D建立六面体网格如图3所示。

图2 边坡数值模拟分析四面体模型

图3 边坡数值模拟分析六面体模型

表1 岩石物理力学参数

表2 模型尺寸参数表

为保持所建立的边坡模型受力平衡，采用位移约束的方式将模型边界条件设置为：前、后、左和右侧边界均为截离边界，模型前后侧边界固定Y方向位移，模型左右侧边界固定X方向位移，模型底部固定Z方向位移，坡面为自由面。

采用强度折减法对边坡模型展开分析，边坡剪切应变增量云图如图4所示，图中还包括边坡的安全系数和速度矢量图，速度矢量图显示出了边坡产生滑动时的滑动趋势。

从图4中可以清楚地看到塑性贯通区域，通过速度矢量图进一步验证了这一判断：处于滑动面外侧各网格点的速度均大于其他区域[18]，表明该边坡已出现滑动，边坡稳定结构发生破坏，同时从图4中可以得到此时相应安全系数为1.80。图5为六面体剖分的边坡模型模拟结果，其安全系数为1.70，且在坡顶上方出现了应力集中现象。与FLAC3D自带的六面体网格剖分程序相比，四面体网格在进行剖分时，网格单元数量多，虽然模拟过程中耗时比六面体网格长，但计算精度相比于六面体而言计算精度会有所相应的提高。而且四面体网格具有较为均匀的疏密程度，能够很好地模拟复杂的地质体，不容易引起应力集中。

图4 边坡剪切应变增量云图及速度矢量图

图5 六面体网格剖分下边坡剪切应变增量云图

图6为露天矿边坡强度折减后边坡位移等值云图和位移矢量图。位移等值线图形态表现为从边坡顶部斜切进入，并与坡面相交，等值线拐点处的切线近似与坡面平行，位移最大部分集中在边坡中上部靠近坡面处，而且可以明显看出边坡上部靠近坡面位移矢量近乎与坡面平行，表现为“剪切”，中部和下部位移矢量在渐近坡趾处表现为“剪出”。这些现象都表明，边坡潜在破坏以圆弧形剪切破坏为主。

图6 边坡位移等值云图和位移矢量图

3.3 可靠性分析

采用强度折减法使边坡达到临界状态时，其潜在滑动面附近等值线最为密集[19]。根据边坡剖面位移等值云图，确定等值线最为密集区域的位移值的范围，利用FLAC3D程序内置的编程语言FISH编制程序，搜索并保存等值线最为密集区域的数据点坐标，利用Origin处理数据进行拟合，得到的结果如图7所示，其中各个离散点为等值线密集区域的点，曲线为该边坡简化的潜在滑动面。在此基础上对该边坡展开可靠度计算。采用Fiessler迭代计算步骤编制边坡可靠度计算程序，程序用C++语言编程实现。该露天矿边坡剖面滑动面示意图见图8，极限状态函数为式(13)。

图7 等值线密集区域离散点及其拟合线图

图8 边坡计算剖面示意图

Z=g(φ1,φ2)=W1×cosα×tanφ1+

W2×cosα×tanφ2+C2L2+C1L1-

(W1+W2)×sinα=0

(13)

式中：φ1、φ2—内摩擦角，°；W1、W2—潜在滑动面质量，N/m3；C1、C2—黏聚力，N/m2；L1、L2—潜在滑动面长度，m；α—滑动面倾角，°。

在诸多不确定因素中，物理力学参数对边坡的安全稳定性有着至关重要的影响，而且为了减少计算的复杂性，故选取对边坡稳定性影响较大的因素作为随机变量，取φ1、φ2、α为随机变量，该边坡岩体相关力学参数如表3所示。

表3 边坡岩体相关参数

采用可靠指标法对该边坡的破坏概率进行迭代计算，迭代7次后，可靠度指标β值达到收敛。求得可靠度指标β=2.381 8，其中基本随机变量X1为白云岩内摩擦角，X2为火成岩内摩擦角，X3为滑动面倾角。根据Pf=φ(-β)=1-φ(β)，求得破坏概率Pf=0.865 6%。现有研究成果表明，露天矿总体边坡可接受的破坏概率一般在0.3%～1.0%之间[20]。表明该边坡在安全系数达到1.80的情况下，破坏概率Pf为0.865 6%，属于稳定边坡，破坏概率较低。

4 结 论

1)本研究基于数值模拟平台，建立了数值模拟和可靠度理论相结合的综合分析方法，对边坡稳定性展开分析。弥补了单一分析方法不足以有效评定边坡稳定性的缺陷。

2)对边坡模型采用限定Delaunay四面体网格剖分，生成了高质量的四面体网格模型。将四面体剖分与六面体剖分的数值模拟结果进行对比分析，表明四面体剖分的优越性。

3)采用FLAC3D内置的FISH语言编程，在强度折减法的基础上，自动搜索保存滑动面附近的数据点，具有简便实用和速度快的特点。

4)将该方法应用于某露天矿边坡稳定性分析，得到该边坡在安全系数达到1.80时，仍有0.865 6%的破坏风险，属于稳定边坡。表明了该方法的可行性。