基于CSI 和加权混合回归的室内定位方法*

李芬芳汝春瑞党小超郝占军

(1.西北师范大学计算机科学与工程学院，甘肃 兰州730070；2.甘肃省物联网工程研究中心，甘肃 兰州730070)

无线通信技术作为现阶段应用最广泛的通信技术，受到不同研究领域越来越多的关注。 位置服务涉及对监测对象的定位、追踪和监测。 关于定位的应用范围和应用需求在不断扩大，如何有效获得研究对象的位置信息，已成为研究人员探究的热点话题[1]。 多年来，Cell-ID 定位技术和全球定位系统(Global Positioning System，GPS)等室外定位技术为人们的生产和生活提供了很多方便，但这些定位技术普遍存在附加噪声和多径衰落干扰等问题，因此，在噪声和多径衰落干扰较大的室内环境中，要通过这些传统的定位技术获得精确的定位存在诸多困难[2]。 随着定位技术的不断发展，各行业对室内定位技术的要求越来越高，应用的领域也越来越广泛，这些需求和应用的不断涌现，均表现出室内定位技术的应用价值。 比如在消防救援中，可以快速并准确地找到被困者的位置，然后以最快的速度展开救援。 室内定位技术在多径衰落较明显的室内环境下的应用需求，表明了其具有较好的应用前景[3-4]。

自20世纪90年代起，各类室内定位技术不断涌现，如基于红外线的室内定位、基于无线电测距的室内定位、基于无线射频识别的定位、基于毫米波和基于蓝牙的室内定位等。 这些方法的特点是需要用户携带额外的信号采集、接收设备，或者需要统一部署相关专业的基础设施，这使得定位系统的普及和应用具有局限性，且定位成本较高[5-7]。

为了克服室内定位环境中多径干扰的问题，现阶段人们将研究重点转向以Wi-Fi 信道状态信息(Channel State Information，CSI)为指纹的室内定位。CSI 描述了Wi-Fi 信号是如何以OFDM 子载波粒度通过多条路径从发送端(Transmit，TX)传播到接收端(Receive，RX)。 CSI 是细粒度的物理层信息，提供的信息丰富且稳定性高，具有更好的细节感知能力及更强的抗干扰能力，故更适合用作指纹，目前已成为Wi-Fi 感知研究中的主流感知载体[8-10]。 与感知粒度有限的接收信号强度(Received Signal Strength，RSS)相比，CSI 有诸多优势。 ①CSI 对周围环境的变化更加敏感，并且能提供高精度的信息，可以实现细粒度感知，也更加符合未来研究的应用需求；②CSI 有效描述了每个子载波的幅度和相位，为研究人员提供了更加丰富的感知信息；③由于使用了正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术，CSI 不易受到多径效应的影响。 所以，CSI 可以看作经OFDM 技术调制后的RSS 信息[11-14]。

多年来，人们对室内定位技术进行了诸多研究，CSI 作为较主流的信号特征，也不同程度地提高了室内定位任务的相关性能。 党小超等[15]提出一种适用于复杂室内环境的定位方法，该方法首先分析了非视距环境下CSI 振幅的不稳定性和CSI 相位误差的来源，并通过计算每个载波链路的相位差选择稳定的链路信号，对相位进行误差校准后用于定位。周明快等[16]认为相位和幅度信息可以相互补充，提出一种基于CSI 相位信息优化的定位算法，将幅度信息和相位信息拼接成一个特征矩阵后用SVM 进行训练，相较于采用单一特征的定位，其准确性和稳定性都得以提高。 Wang 等[17]提出了DeepFi 定位系统，将三个天线上的CSI 数据通过深度学习模型训练，得到不同位置的权重作为指纹，有效降低了定位误差。 李方敏等[18]提出一种基于距离测量和位置指纹的室内定位方法，该方法先用距离测量算法对指纹进行过滤，然后通过k 近邻算法进行指纹匹配，既减少了指纹匹配过程中的计算量，同时也改善了定位精度。 Rao 等[19]提出了一种基于矩阵相似性的定位算法，该算法首先计算测试点与参考点CSI 矩阵之间的相似度，然后选择相似度最大的参考点坐标作为最终的定位坐标。 刘颜星等[20]提出一种基于CSI 信号的被动式室内定位算法，该算法首先通过方差补偿的自适应卡尔曼滤波算法对数据进行过滤，然后使用二分K 均值聚类算法进行分类，该算法同时考虑了CSI 信号的幅值和相位特征。周牧等[21]采用无偏估计理论和费歇尔信息矩阵的性质，从CSI 的频域角度推导了不同异步效应下的克拉美罗下界，同时推导了CSI 定位误差界的闭合表达式，最后通过调整参数来评估定位性能。 李新春等[22]提出一种基于KPCA (Kernel Principal Component Analysis)和改进GBRT(Gradient Boosting Regression Tree)的室内定位算法。 通过KPCA 提取指纹向量的主成分特征，将训练集分为多个子训练集，每个子训练集在GBRT 上训练一个子回归模型，最后形成一个强回归模型，然后在该模型上预测目标的位置信息。 党小超等[23]提出一种基于SVM 回归的室内定位方法，该方法首先采用PCA 提取指纹特征，然后建立CSI 指纹与目标位置之间的SVM 回归模型，实现对测试集数据的预测。 朱莹等[24]提出了一种结合CSI 和接收信号强度指示(Received Signal Strength Indicator，RSSI)数据的定位方法，采用贝叶斯过滤法处理数据来提高室内定位精度。

以上这些方法大多是将CSI 幅值和相位进行相关处理后作为位置指纹，或者通过机器学习或深度学习算法的训练获取位置指纹，或者得到定位模型；另外，也有将CSI 和RSSI 信号相结合的定位方法。我们知道，深度学习方法在模型训练过程中，需要较大的数据集，这在本文应用中有一定的局限性。 大多数机器学习方法可以在小样本上进行训练，所以，本文通过引入机器学习方法研究室内定位技术。 在传统室内定位中，研究人员通常是在单一的机器学习方法上进行研究和比较，然后选择定位误差低的模型用于仿真，而不是考虑融合多种方法进行室内定位技术的研究[25]。 基于上述现状，本文考虑现实环境的多变性，提出一种基于支持向量回归(Support Vector Regression，SVR) 和K 近 邻 回 归(K-Nearest Neighbor Regression，KNR)的加权混合回归(Weighted Mixed Regression，WMR)的室内定位算法WMR＿SKR。 该算法分为两个阶段，分别是离线训练阶段和在线测试阶段。 离线阶段是收集CSI 数据并用训练集数据对定位模型进行训练，首先分别训练SVR 和KNR 定位模型，这两种定位模型的权重系数之和为1，通过多次定位误差测试，根据测试结果确定两个模型的权重系数，最终得到WMR＿SKR 的参数。 WMR＿SKR 模型结合了SVR 适合小数量样本数据集的特点，有效验证了KNR 对研究数据没有假设的优点，同时规避了其计算量大的缺点。

1 CSI 信息采集与提取

CSI 信息是采用OFDM 技术对信道状态的估计，也是对信道频率响应(Channel Frequency Response，CFR)采样的结果。 根据CSI 提供的当前通信系统信道状态，改变系统的传播策略，可以为多天线系统中高可靠、高速率的通信提供保障[26]。 OFDM 技术的发展使得CSI 开始被挖掘，研究人员分别在Intel 5300和Atheros 商用无线网卡上提取出物理层的CSI，这为基于Wi-Fi 的室内定位和感知研究提供了可能。 与仅包含接收信号幅度信息的RSSI 相比，CSI 有更多的优势[27]。 OFDM 系统被建模为:

式中:Y是接收信号矢量，X是发送信号矢量，H是信道增益矩阵，N是高斯白噪声矢量。 CSI 的估计值可以根据式(1)表示为:

在通信信道中，每条传输链路上的每个子载波都对应一个CSI 值。 在MIMO 系统中，若接收天线数量为R，发送天线数量为T，OFDM 系统中的子载波数量为n，那么接收端收到的每一个数据包中的CSI 信息将是一个T*R*n维的矩阵，该矩阵包含了当前信道完整的信道状态信息。 每条链路上的CSI 测量可以概括为:

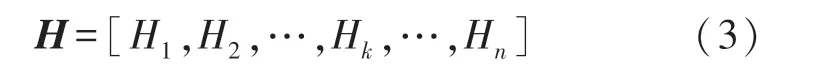
式中:n为子载波数量，Hk为第k个子载波的CSI值，通常为一个复数，其值可以表示为:

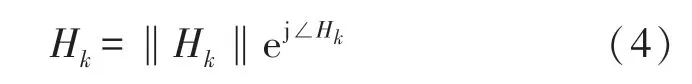
式中:‖Hk‖和∠Hk分别表示第k个子载波的振幅和相位。

本文发送端采用1 根天线，接收端采用3 根天线，因此共有3 条数据链路，通过CSITool 工具修改Intel5300 无线网卡驱动程序，从OFDM 系统中读取30 个子载波的CSI 信息。 图1 所示为三条链路上的CSI 信息，横坐标为子载波索引，纵坐标为CSI 幅值。

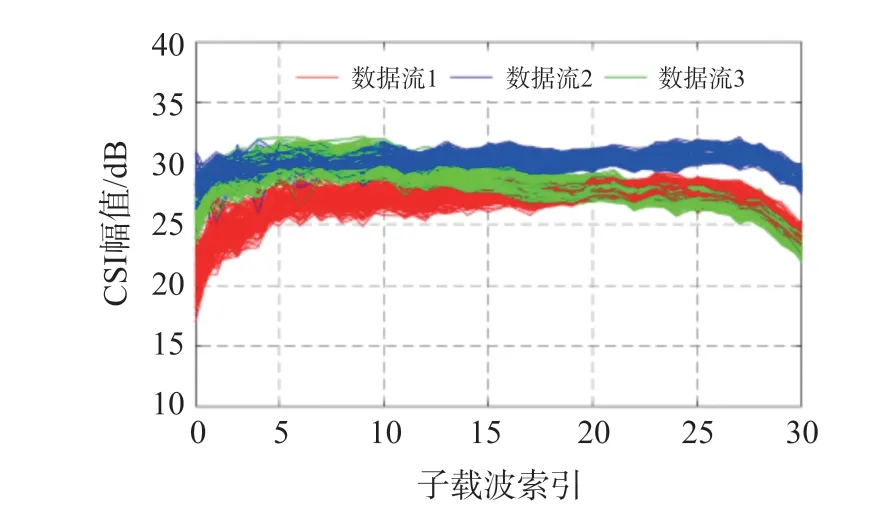
图1 信道状态信息

2 基于CSI 和加权混合回归的室内定位方法

2.1 定位流程

本文提出的基于CSI 和加权混合回归的室内定位方法由离线训练和在线测试两个阶段组成，总体流程如图2 所示。

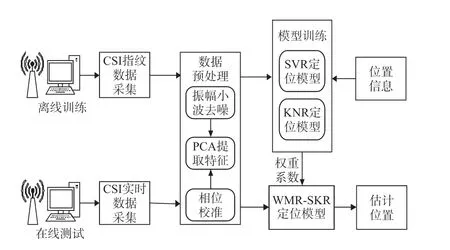
图2 定位流程图

为了得到有效的CSI 数据，在定位流程的两个阶段中都需要对采集的数据进行预处理，本文通过对振幅数据采用小波变换去噪，对相位数据采用线性变换的处理过程获取可用于室内定位的CSI 数据；为了减少数据冗余和计算量，进一步采用主成分分析方法提取特征数据，用于定位模型的训练和测试。 此外，离线训练阶段将预处理后的CSI 指纹信息作为训练数据，结合其对应的物理位置分别训练SVR 定位模型和KNR 定位模型，并根据定位误差对两种模型权重系数进行更新，以获得最优的权重系数；最后根据获得的权重系数得到混合两种模型的WMR＿SKR 定位模型。 在线测试阶段，将处理后的CSI 数据输入到离线训练阶段得到的WMR＿SKR 定位模型中，对人员位置进行估计。

2.2 数据预处理

Wi-Fi 信号室内传播模型如图3 所示，室内环境相对复杂，桌椅、家具、墙壁等静态障碍物的存在导致Wi-Fi 信号不能以直线路径到达接收端，而是经过多条路径到达，此现象被称作多径效应，多径效应使得Wi-Fi 信号在传输过程中产生损耗和衰减。此外，室内其他人员以及射频设备的干扰也会产生较大的噪声。 因此，通过Wi-Fi 设备采集到的原始CSI 数据不能直接用于室内定位，需要对其预先进行处理方可使用。 本文对幅值数据进行小波变换去噪，对相位数据进行线性变换以获得有效的CSI 数据用于室内定位。 为了减少数据冗余，同时提高定位精度，进一步用PCA 方法进行数据降维和特征提取。

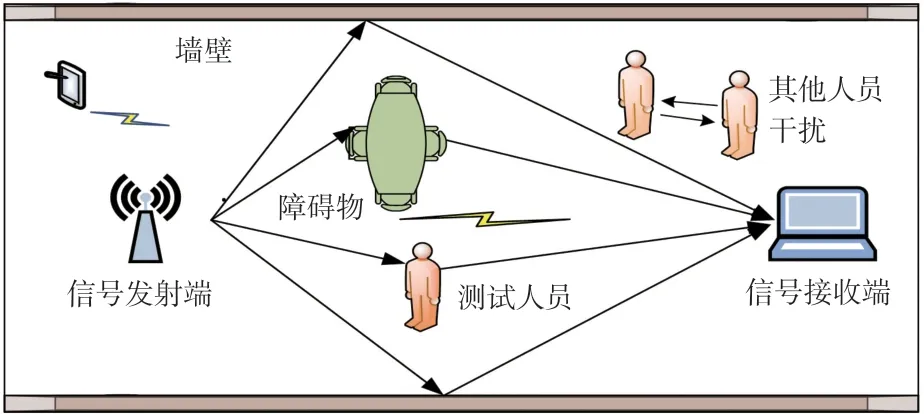
图3 Wi-Fi 信号室内传播模型

2.2.1 幅值数据处理

为了方便观察，实验选取其中一根天线采集到的数据作为对比数据。 图4 为在实验室、会议室、楼道采集到的CSI 数据图，图中的横坐标为子载波索引，纵坐标为幅值，我们可以看到不同场景下的CSI数据差异较大，会议室环境中由于大量桌椅的存在导致信号噪声最大，实验室环境次之；而楼道环境相对空旷，干扰物少，CSI 数据亦更佳。 为了去除这些噪声，在采集到初始数据集后，将CSI 数据中的幅度信息提取出来，对其进行小波变换。 小波变换能够在多个频率尺度上对信号进行分析，对于局部精细的特征具有更好的提取能力。 Chen 等[25]利用小波变换提取不同频段的特征，从而得到对应于身体不同部分的运动速度。 在阈值选择标准上，我们根据极值阈值原则，利用极大极小原理选择了阈值，产生一个最小均方误差的极值。 之后利用db6 小波变换对信号进行5 层分解，得到最终波形。

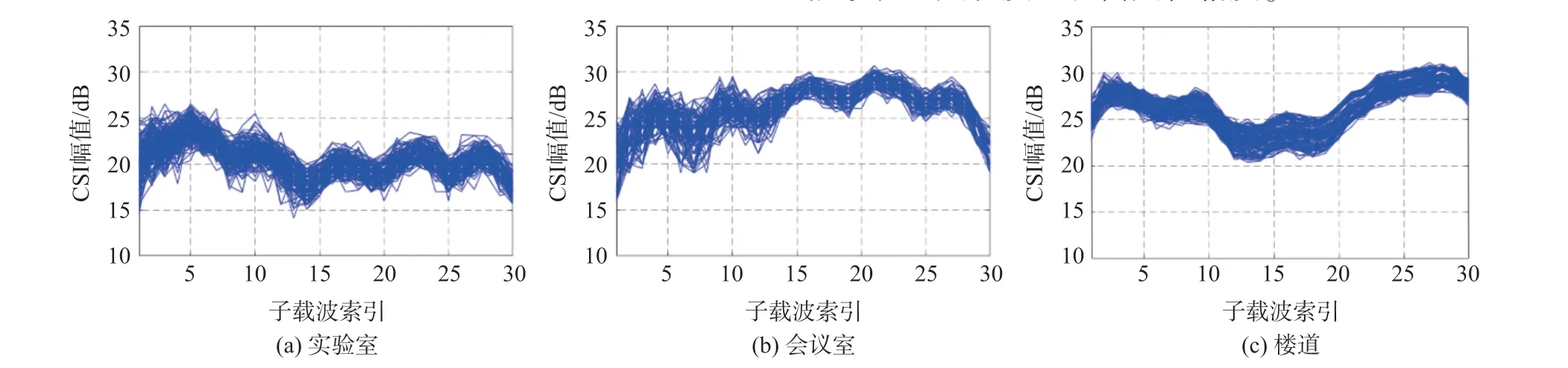
图4 不同场景的CSI 数据比较

图5 所示为三个不同测试环境中的一个数据包经过预处理后得到的CSI 幅值图。 可以看到，CSI幅值信息经过预处理后变得更加平滑和直观，也能更加明显地反应不同实验环境下的数据特征，因此能够在一定程度上提高定位精度。

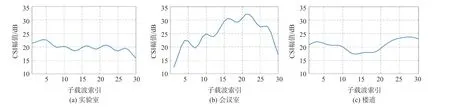
图5 CSI 数据去噪后的CSI 幅值

2.2.2 相位校准

CSI 数据包含幅度信息和相位信息。 在实际测量过程中，由于硬件精度不够高而导致CSI 相位测量误差较大，主要为载波频率偏移和采样频率偏移，因此无法直接使用。 为了获得真实的相位信息，需要对相位进行校准。 假设，第i个子载波的相位信息经过解卷绕后表示为:

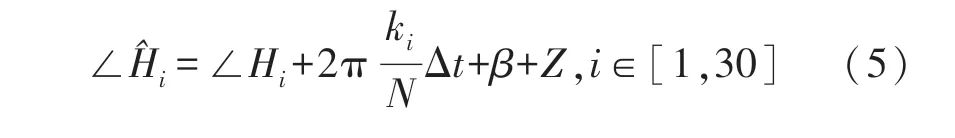
式中:∠Hi是真实相位，Δt是接收端的时间偏移，β是相位偏移，Z是随机噪声，ki是子载波索引，N是快速傅立叶变换(Fast Fourier Transform，FFT)的大小。 如上所述，为了获得真实相位，需要消除测量相位的Δt和β。 通常采用线性变换的方法进行相位校准，首先需要计算整个频带相位的斜率w和偏移b，如下所示:

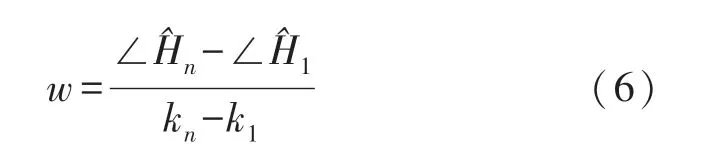
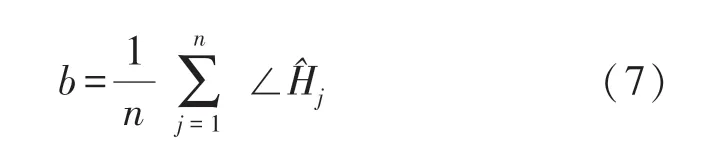
式中:n为子载波数量，通过从测量相位减去线性项wki＋b，我们可以获得真实相位相位校准结果如图6 所示。

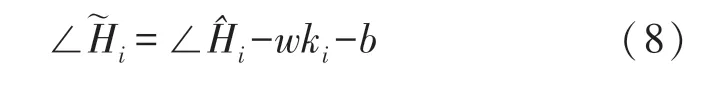
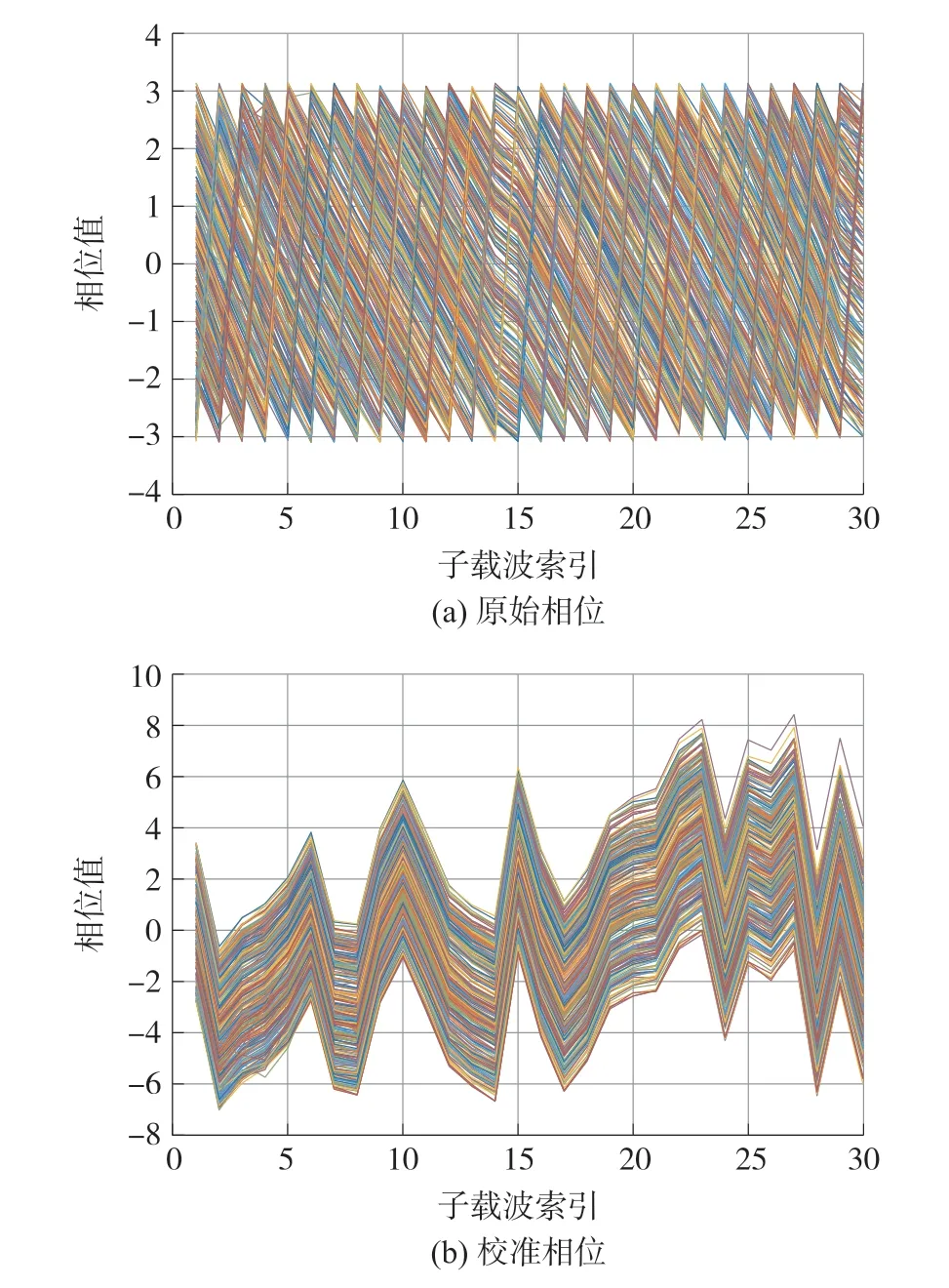
图6 相位信息

2.2.3 特征提取

对于采集到的Wi-Fi 信息，其包含的数据维数太多会使特征匹配过程过于复杂，影响识别精度。 因此，通常需要在数据预处理阶段，对感知数据进行降维处理和特征提取。 本文用PCA 算法对经过小波变换降噪后的幅值和校准后的相位进行数据降维，并选取第一主成分作为提取的特征。 算法提取280 个数据包的主要特征，作为用于定位的幅值和相位特征。PCA 算法有两种实现方法，分别是基于特征值分解协方差矩阵和基于奇异值分解(Singular Value Decomposition，SVD)协方差矩阵。 下面以把n维的数据集M={m1，m2，…，mn}降到k维为例，简要说明PCA 方法的实现步骤:①用每个特征减去其平均值，即去中心化；②计算特征值的协方差矩阵(MMT)/n；③求协方差矩阵的特征值与特征向量；④选择特征值最大的k个特征向量组成特征向量矩阵P；⑤将数据转换到k个特征向量构建的新空间中，即Q=PM。

2.3 加权混合回归定位算法

2.3.1 SVM 回归算法之SVR

由于Wi-Fi 信号在传播过程中受多径效应等因素的影响，人在室内不同位置的CSI 信号与物理位置存在一种复杂的非线性映射关系。 SVM 是机器学习中一种适用于小样本分类的算法，支持线性与非线性回归，基于SVM 的回归被称作支持向量回归SVR。 在本文中，通过SVR 对CSI 样本数据进行回归训练，可以得到CSI 特征向量与位置坐标之间映射关系的数学模型。 假设在各参考点采集的CSI 数据生成的训练样本对为(csii，pi)，pi为坐标(xi，yi)，训练目标即分别构造x和y的线性估计函数φx和φy。 在高维空间中构造目标函数和约束条件如下:

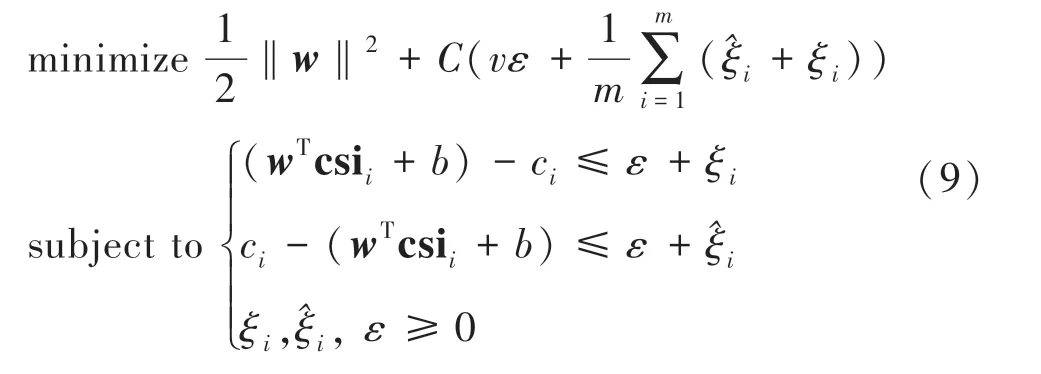
式中:w∈Rl是表示函数方向的向量，b∈R 是表示其位置的常数，csii是CSI 指纹向量，ci是位置坐标大小，对于φx回归ci为x坐标，对于φy回归ci为y坐标。ξi和是松弛变量，用于捕获超过ε误差的部分，同时引入正则化常数C进行惩罚。 求解方程(9)得到以下近似函数:

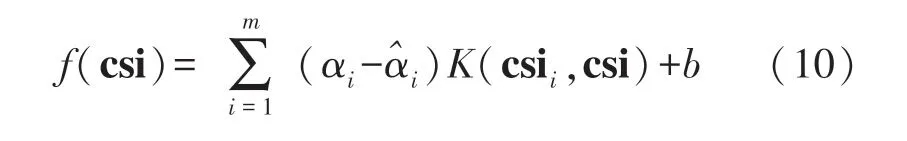
式中:αi和是拉格朗日乘子，K(csii，csi)是核函数。

2.3.2 KNN 回归算法之KNR

KNN 常被用于离散数据的分类和标签预测，当其用于回归时称为K近邻回归(KNeighbors Regression，KNR)，KNR 可以用于对连续的数据标签进行预测，符合本文对位置坐标的预测要求。室内定位过程中的回归是基于距离进行计算的，KNR 算法通过收到的信号特征向量计算与该信号距离最近的k个位置点的距离di，然后采用计算加权均值的方法来预测目标的位置。 本文使用欧氏距离进行距离计算。 假设n维空间中的两个点为X=(x1，x2，…，xn)和Y=(y1，y2，…，yn)，则它们之间的欧式距离为:

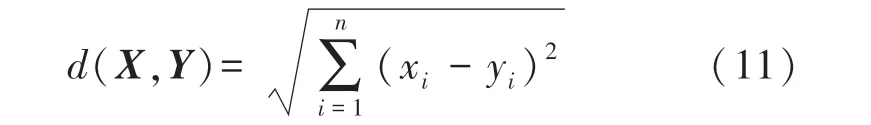
2.3.3 加权混合回归定位算法(WMR＿SKR)

SVR 和KNR 算法是机器学习中常用于构建回归模型的算法，由于每种回归算法都有其优缺点，所适用的场景也有差异，本文基于结合优点、规避缺点的思想，设计了一种基于这两种回归模型的混合回归模型。 本文首先将测试数据分别在SVR 和KNR两种模型上进行训练，训练后分别获得它们的定位误差，根据分析结果，获取这两个模型的符合本文训练数据的最佳权值系数，即可得到回归模型WMR＿SKR。 WMR＿SKR 回归算法实现步骤如下。

①步骤1:在训练数据上分别训练SVR 和KNR回归模型，得到2 个回归模型的最佳模型；

②步骤2:将测试数据分别在KNR 和SVR 回归模型上预测，得到基于两种模型的初步定位结果(x1，y1)，(x2，y2)；

③步骤3:由式(12)计算模型预测获得的定位结果与真实位置(x，y)之间的定位误差。

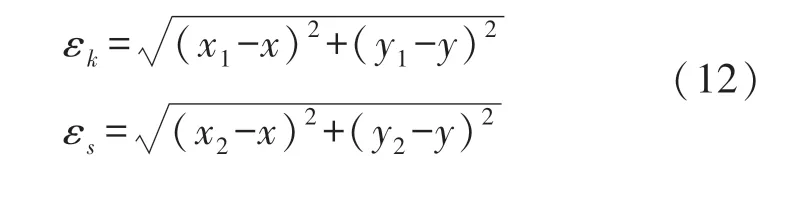
④步骤4:根据定位误差，由式(13)计算KNR回归模型的权值hk和SVR 回归模型的权值hs，其值满足hk＋hs=1。

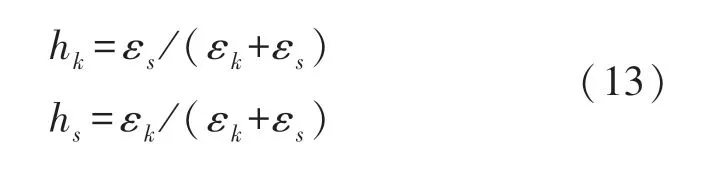
⑤步骤5:定位结果(X，Y)如式(14)计算得到:

3 实验结果与评估

3.1 实验场景

本文在实验室、会议室和楼道三种实验环境下进行测试。 其中，将障碍物较多、多径效应较强的实验室和会议室，作为非视距环境。 将一个宽度为2 m的楼道，作为视距环境。 真实实验场景及其平面图如图7 所示， 图中的圆点表示预先设置的参考点位置。 使用两台安装了Intel 5300 无线网卡和Ubuntu 14.04 LTS 操作系统，CPU 型号为Intel Core i7-8700 的台式机分别作为发送端和接收端，两端天线高度均为1.5 m。 在测试过程中，将设备设置为Monitor 模式，工作频率为5 GHz。 在实验中，尽量让测试人员保持稳定后再进行数据采集，采集的过程中周围环境基本保持不变，一定程度上降低了环境对信号的干扰。 信号发射端向接收端发送280 个连续数据包，收集各参考点的CSI 数据，得到初始数据集。

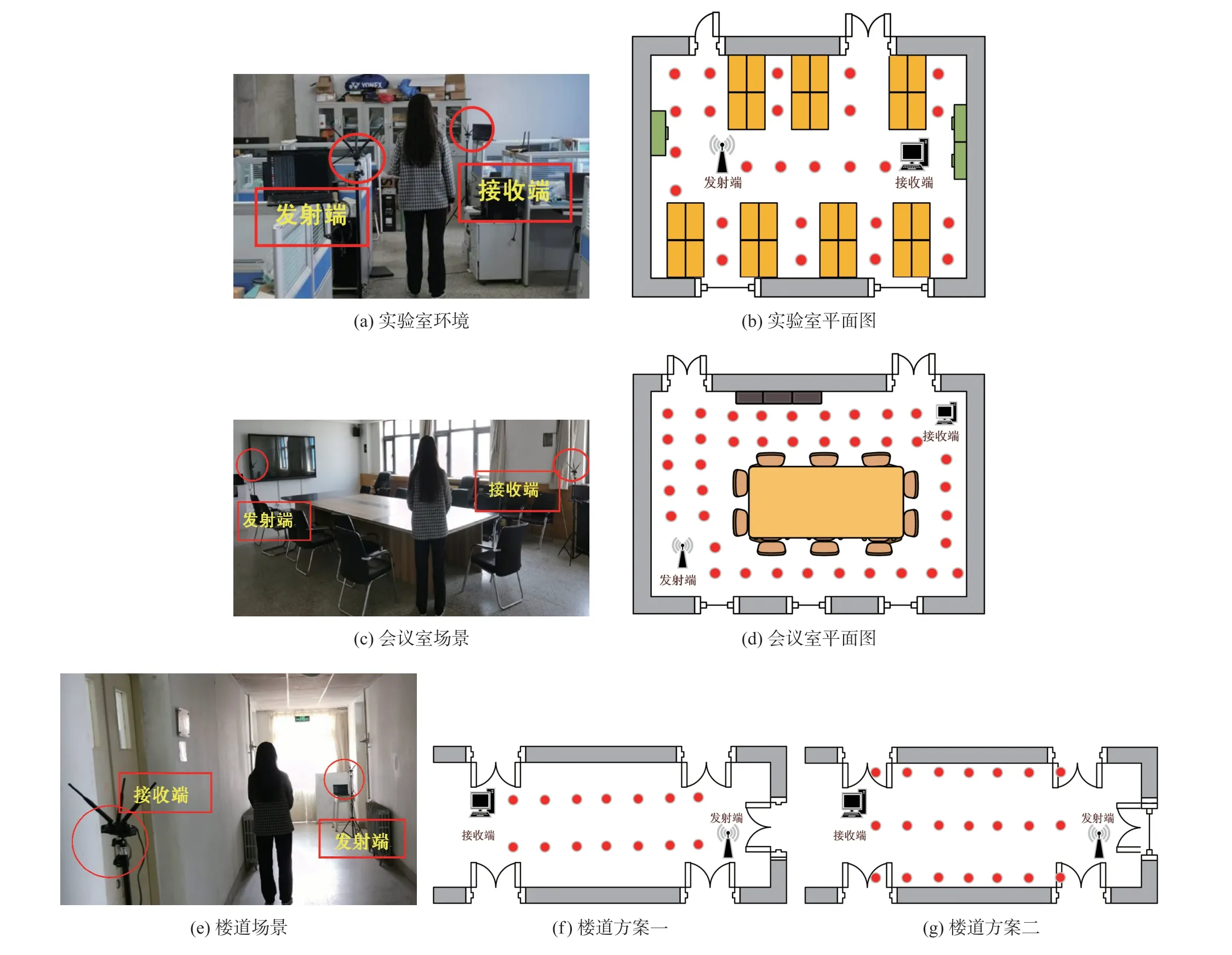
图7 实验场景

3.2 性能分析

为了验证本文提出的基于CSI 和加权混合回归的室内定位方法的综合性能，从以下几个方面进行了相关实验和分析，主要通过计算不同情况下的定位误差累积分布函数(Cumulative Distribution Function，CDF)和定位误差来评估定位性能。

3.2.1 整体定位性能分析

本文在实验室、会议室和楼道三种真实环境下进行实验测试，结果如图8 和图9 所示。

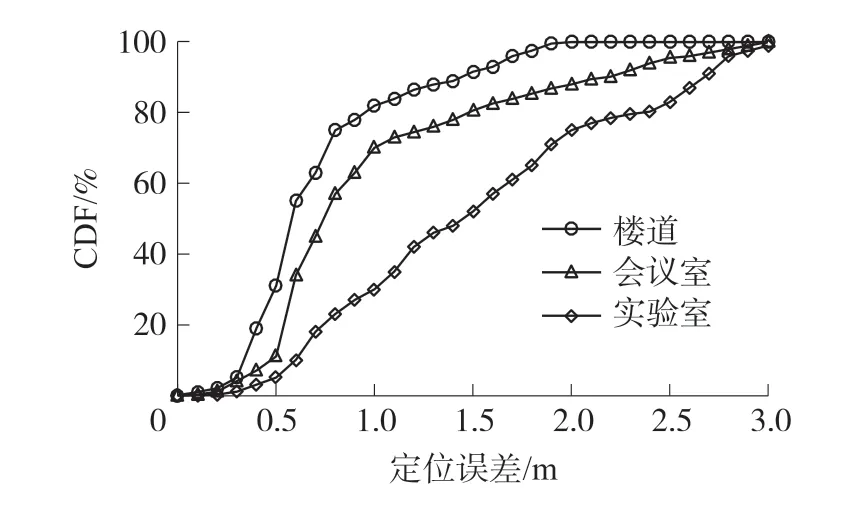
图8 不同环境定位误差CDF

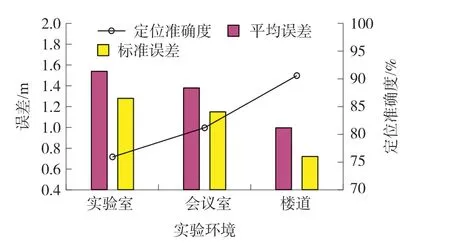
图9 不同环境定位误差及准确度

我们可以看到，三种定位环境下，楼道的定位精度和准确度最高，这是由于楼道相对空旷，障碍物较少，信号干扰较小；而实验室和会议室环境复杂，多径效应较强，导致定位误差较大。 此外，实验室经常有人员走动，办公桌数量多且较为高大，同时电脑和手机等设备对Wi-Fi 信号的影响也较大，因此实验室定位的误差最大。 总体而言，在视距环境(楼道)和非视距环境(会议室)中，本文定位算法分别可以在91.6%和80.6%的概率下达到1.5 m 的定位精度，且平均误差和标准误差均小于1.5 m。

3.2.2 参考点数量对定位结果的影响

为了研究参考点数量对定位结果的影响，本文选择楼道为本文的实验环境，共做了两组实验，一组是在楼道选取14 个参考点，即方案一(图7(f))；另一组参考点个数为21，即方案二(图7(g))。

从图10 可以发现，方案一比方案二的定位效果好。 方案一在82%的情况下定位误差为1 m，91.6%的情况下定位误差为1.5 m，而方案二只有75.1%的情况下定位误差达到1 m，86.7%的情况下定位误差为1.5 m。 一般而言，参考点数目越多时定位误差应该越小，但是，由于楼道两侧就是墙壁，若参考点距离墙壁太近，CSI 信号会受到较大影响，导致代表性不强。 方案二中虽然参考点数目较多，但其在位置选择上不及方案一有优势，因此定位性能下降。 此外，由于参考点数量对模型训练所需时间有影响，方案二的定位比方案一耗时更长，所以在后续的实验中，为了保证较好的定位性能，选择方案一作为楼道环境的对比实验。

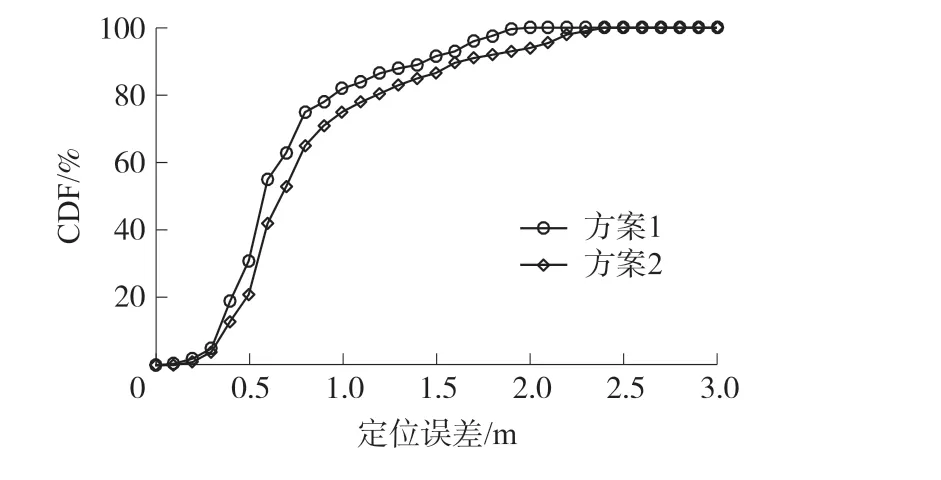
图10 不同参考点数目的定位误差CDF

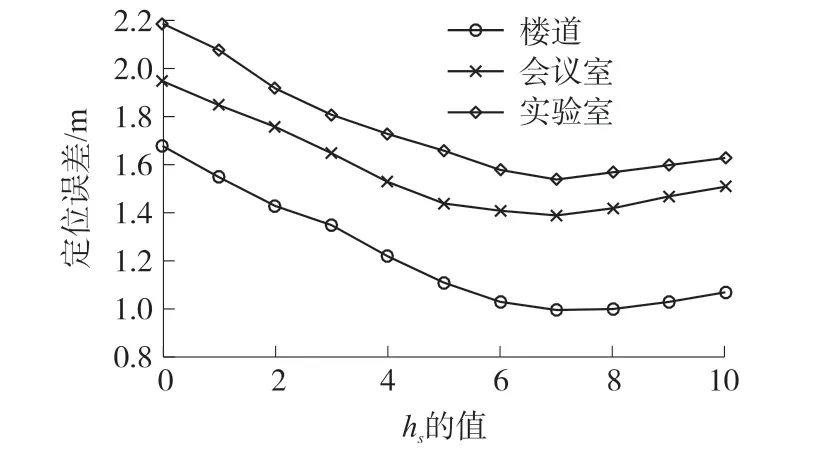
图11 SVR 的权重系数与平均定位误差的关系

3.2.3 权重系数对定位性能的影响

本文提出的加权混合回归定位方法结合了SVR 和KNR 两种算法的定位结果，两者权重系数的选取直接影响到最终的定位精度。 由于KNR 的权重系数hk与SVR 的权重系数hs之和为1，hs增大也就意味着hk减小，为了寻找最优的权重系数，通过大量实验统计分析hs取不同值时的定位误差，结果表明，当hs的值为0.693 时，WMR＿SKR 的平均定位误差最小。

3.2.4 SVR 核函数对定位性能的影响

为了说明高斯核函数在回归定位中的适用性，同时获取WMR＿SKR 模型更好的参数，本实验从核函数的角度分析了SVR 模型适用的参数。 核函数在回归定位算法中占据着重要位置，通过不同核函数构建的支持向量回归函数也会存在差异。 本文在楼道实验环境中，对比了SVR 模型在采用不同核函数时定位模型的误差CDF 值。 实验结果如图12 所示，可以发现在采用基于高斯核函数的SVR 定位时，模型的定位误差最小。 我们知道，高斯核函数在描述诱导空间的非线性关系方面很有优势，更适合描述CSI 数据特征与物理位置之间的非线性关系，因此，在后续的实验中，SVR 模型采用高斯核函数作为其核函数。

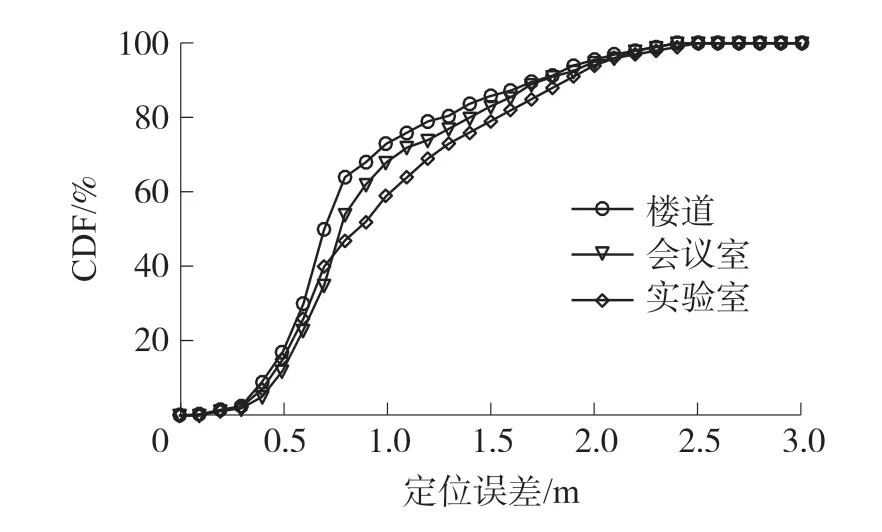
图12 不同核函数SVR 算法的定位误差CDF

3.2.5 定位算法比较

为验证本文提出的WMR＿SKR 算法的性能，在楼道环境中，对于经过相同预处理的CSI 数据，分别使用应用最广泛的几种机器学习算法进行定位测试，如图13 所示。 从实验结果可以看到SVR 算法的定位精度优于SVM，KNR 和KNN 三种算法，而WMR＿SKR 算法结合了SVR 和KNR 两种算法的优势，其性能更加优于这几种算法，定位误差在1 m 以内的概率达到82%，而其他算法都在75%以下。 由此证明WMR＿SKR 模型结合了SVR 适合小数量样本数据、可以解决高维问题的优点，以及KNR 对数据没有假设的优点，同时规避了其计算量大、样本不平衡和需要大量内存的缺点。

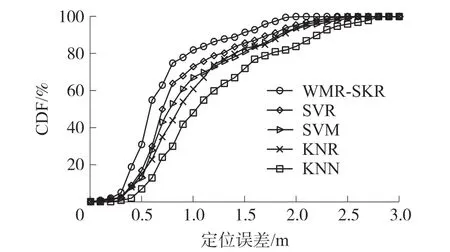
图13 不同算法的定位误差CDF

4 结束语

针对现阶段回归定位算法存在的差异，本文提出了一种基于CSI 和加权混合回归的室内定位方法。 该定位方法分为离线训练和在线测试两个阶段。 离线阶段，将采集的CSI 信息经过预处理，输入到SVR 和KNR 模型中分别训练定位模型，并根据定位误差对两种模型权重系数进行更新优化，将两种模型的定位结果乘以对应的权重系数再求和，得到最终的WMR＿SKR 定位模型。 在线测试阶段，将获取的预处理后的CSI 实时数据输入到训练好的WMR＿SKR 模型中进行位置估计。 我们在实验室、会议室和楼道三个不同环境中进行实验验证，实验结果表明本文提出的定位方法有效结合了两种回归算法的优点，且提高了定位精度。