基于激光跟踪仪多站位布局的标准场参考点可靠性分析*
胡晓磊 张丰 任瑜 平少栋 / .上海市计量测试技术研究院;.中国计量大学计量测试工程学院
0 引言
如何将零件快速可靠地拼接成总成件是大型部件装配中最常见的问题[1]。为解决该问题,首先要考虑如何高效、可靠地测量零件上的特征点(与工艺特性相关的点)。通过将特征点可靠的测量数据反馈给工业机器人的执行机构,以减小装配过程中存在的偏差,进而保证总成件装配的可靠。三维空间坐标标准场的参考点作为特征点测量的支撑,可满足大型部件装配中快速可靠的测量要求,因此,标准场参考点的稳定可靠成为大型部件测量准确的前提和基础。
结合某测量现场的工装环境,三维空间坐标标准场参考点布局如图1所示,平面中灰色标志表示地面参考点,深色标志表示型架参考点,O(ERS36)为坐标系原点。大型部件的装配位置处在标准场一至三层空间中,该布局方案满足三维空间坐标标准场全覆盖工装的测量需求。标准场参考点的分层布设情况如表1所示。此外,在采用分层布设参考点的同时,也应选择较为稳定的立柱或有支撑的悬梁结构等。
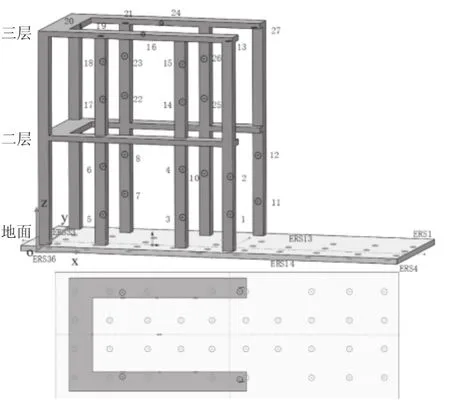
图1 参考点布局
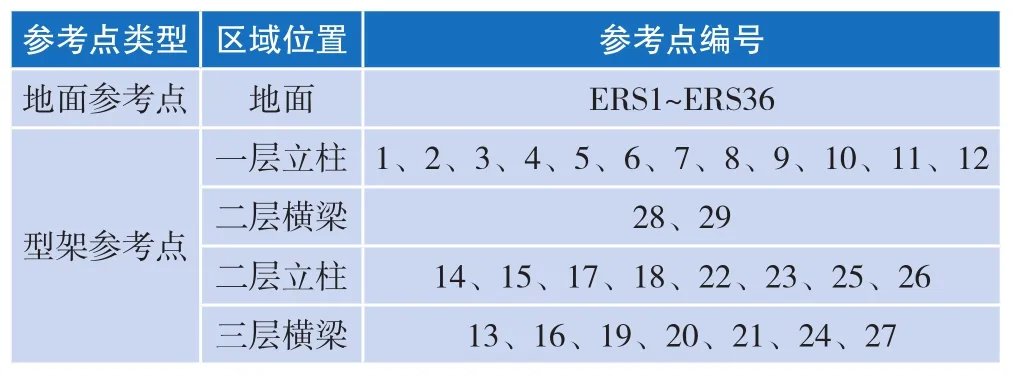
表1 标准场参考点的分层布设
1 标准场测量方案
根据标准场中参考点的分层布设情况,结合现场的型架布置区域,设置以下测量方案:
1)如图2所示,在1~10站位分别架设激光跟踪仪,交叉测量标准场中的参考点(地面参考点+型架参考点)[2-6];
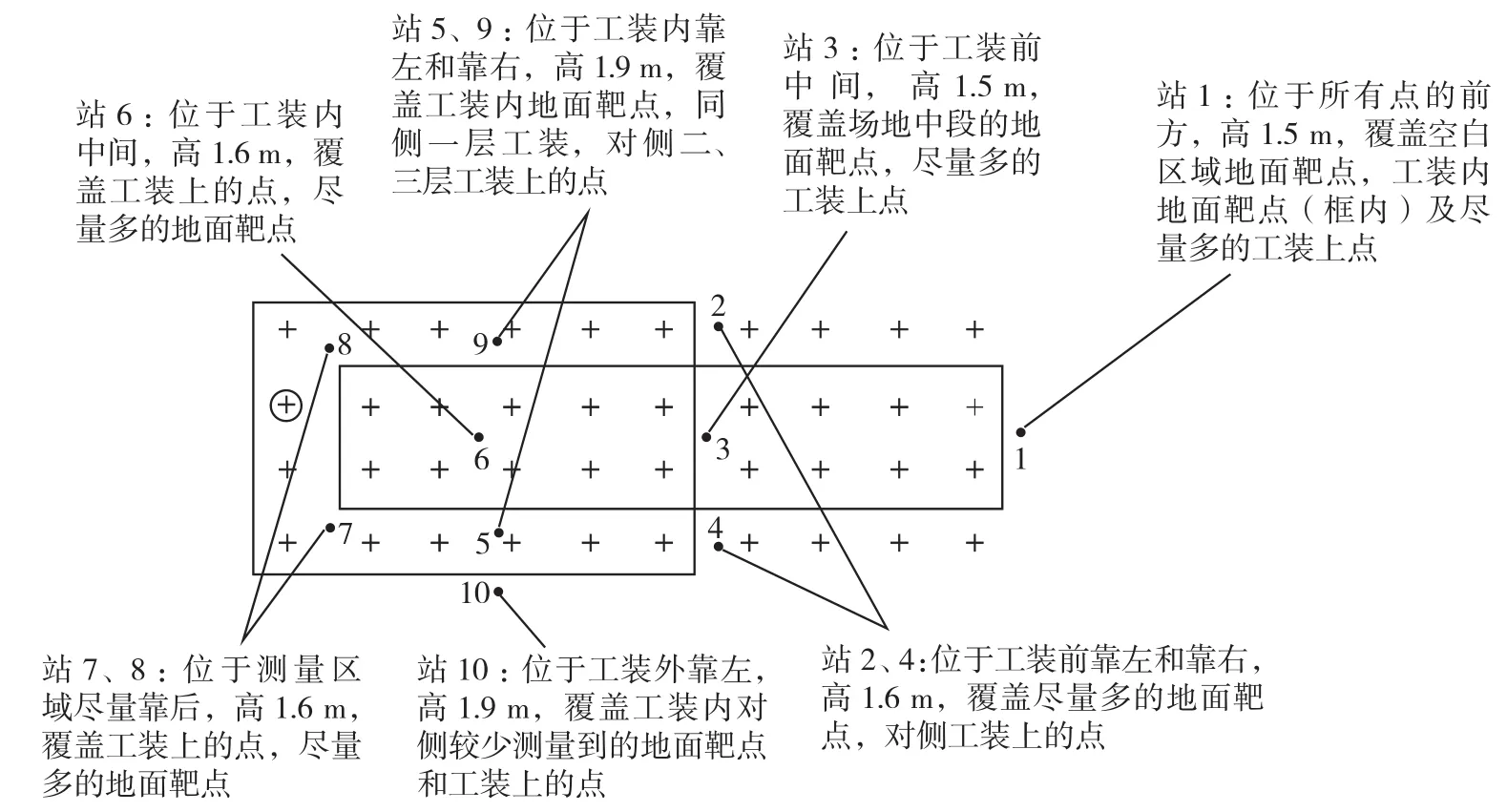
图2 激光跟踪仪站位布局
2)测量周期不少于6个月。
2 数据评估方案
针对测量方案中多站位获取的测量数据,将其融合到同一坐标系中,进行测量数据的对比分析。多源数据融合模型解决了多台仪器测得值合成结果的坐标值问题,是一个多目标优化模型,由各个站位的仪器和测得值构成的约束方程组成[7]。基于多源数据融合模型开发了多源数据融合软件,该软件在Visual Studio 2013平台下,采用C++语言开发,可实现组合测量中的多源数据融合。通过设置测量仪器的参数并输入来自不同测量仪器的测量数据,由软件自动将数据整合至同一坐标系中,计算点的坐标值并评定其测量不确定度。
按照上述实验方法,某日期某台激光跟踪仪经多站位融合后输出的点坐标为pγk=(xγk,yγk,zγk),其中γ表示日期,k表示参考点编号。可通过不同日期实测数据的各分量偏差及点位偏差进行初步分析,再利用参考点ki距坐标原点距离值的标准偏差来评估参考点的可靠性。
X/Y/Z分量均值:

式中:N——所选日期的个数
不同日期下的X/Y/Z分量偏差:
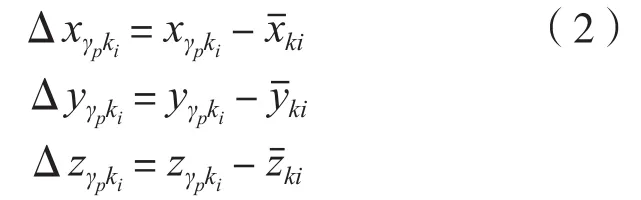
由式(2)可得参考点ki的点位偏差:
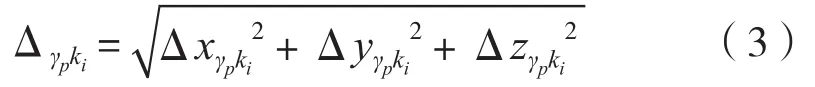
计算参考点ki距坐标原点距离值的标准偏差:

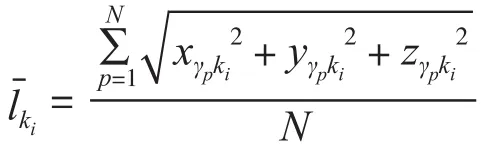
根据式(4)计算得到标准偏差Ski,设定阈值λ可评估参考点的可靠程度,即若Ski≤λ,认为该参考点状态可靠,反之则认为该参考点存在较大波动,不建议继续使用。
3 实验方案实施
3.1 实验过程
实验周期为:2019年12月5日~2021年6月11日,其中有效数据13组,涵盖了8个不同时段。
3.2 实验数据采集
在整个实验过程中,利用SA软件实现不同站位下参考点测量数据的采集,截取的部分工程案例如图3所示。
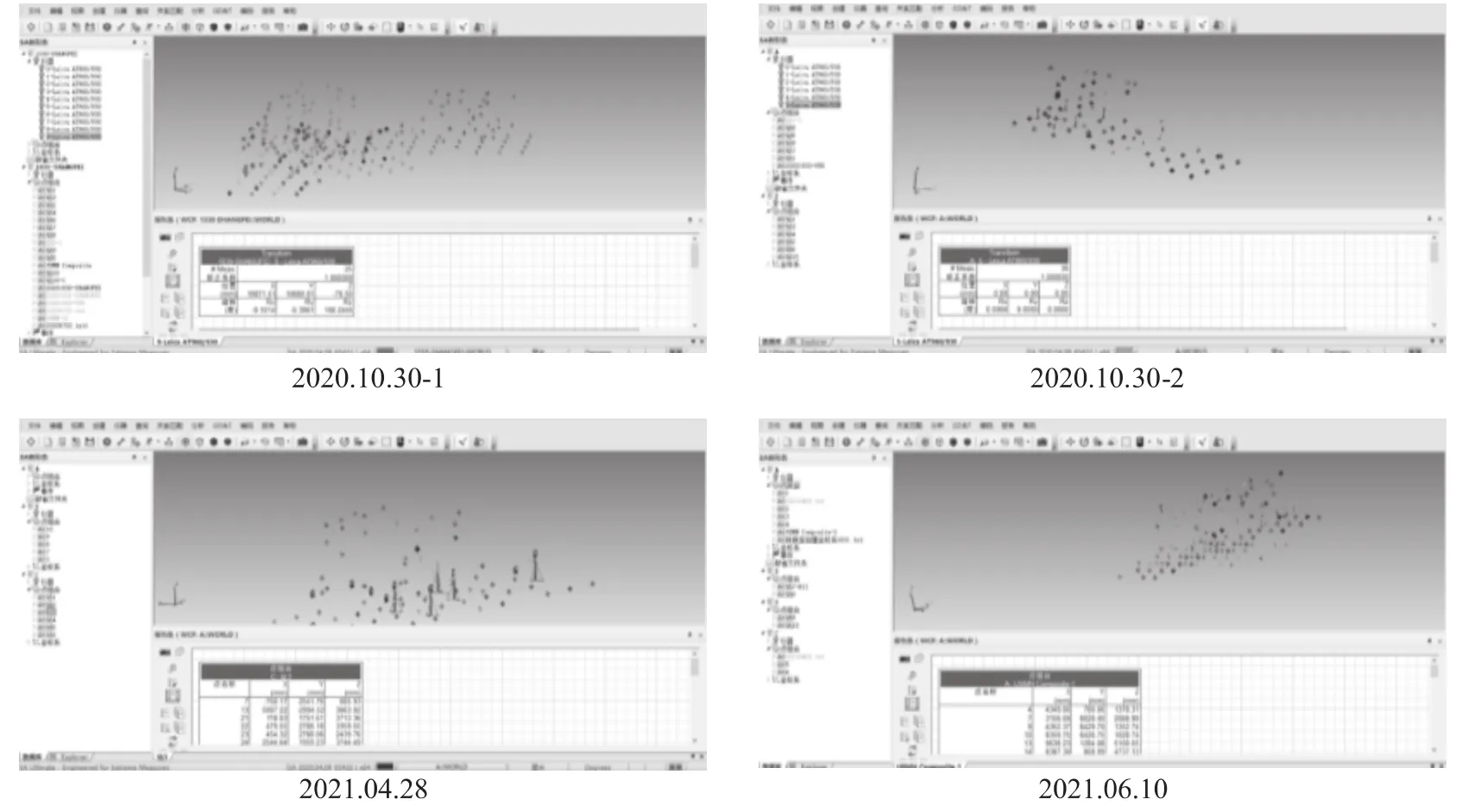
图3 工程案例(截取部分)
4 标准场参考点的坐标分析
选取7组不同月份的实测数据,结合数据评估方案,得到X、Y、Z的分量偏差及点位偏差,如图4~6所示。
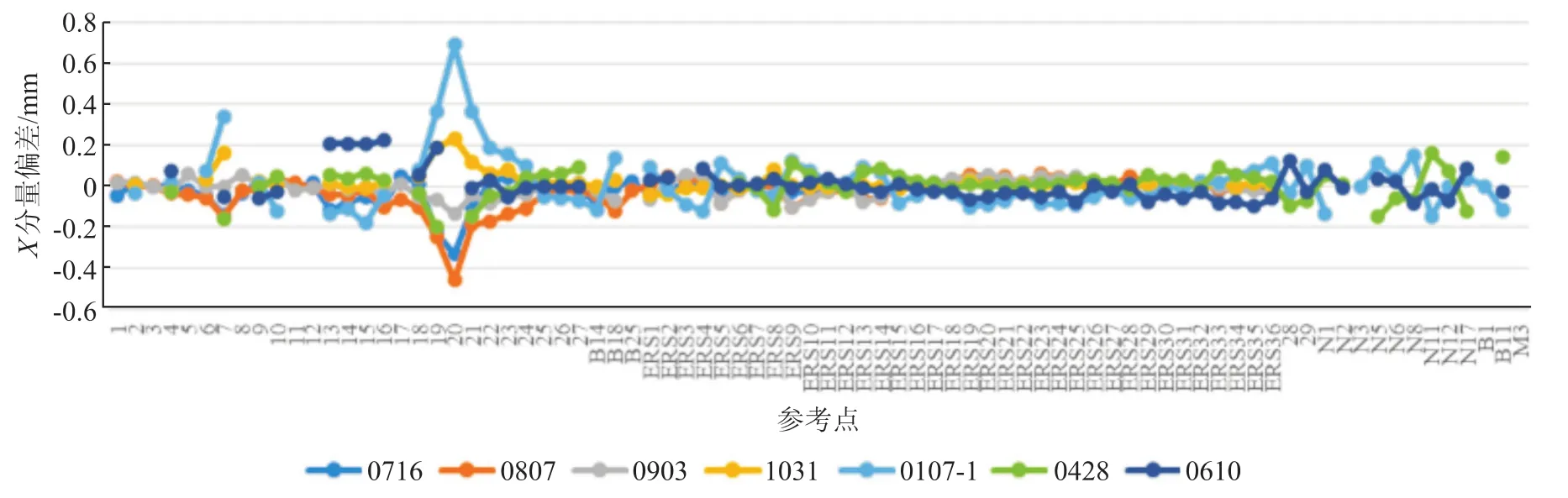
图4 X分量偏差
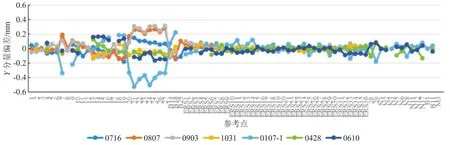
图5 Y分量偏差

图6 Z分量偏差
由图4~6可知:X分量偏差绝对值最大为0.692 mm(点20),Y分量偏差绝对值最大为0.525 mm(点21),Z分量偏差绝对值最大为0.440 mm(点27);对于所有参考点而言,Z分量偏差较X、Y分量偏差离散程度大,说明标准场的Z方向较X、Y方向波动情况严重;地面参考点的X、Y、Z分量偏差相对于型架参考点离散程度小,具有较好的可靠性。由图7可知,型架上的19~27号点点位偏差较标准场中的其他参考点离散程度大,偏差值最大可达到0.767 mm(点20),而其余参考点的点位偏差基本在0.2 mm左右。
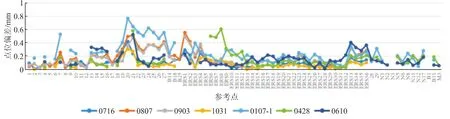
图7 点位偏差
各参考点距离值的标准偏差如图8所示,地面参考点的标准偏差整体小于型架参考点,因此,地面参考点更为可靠。此外,仅对于型架参考点而言,一层的参考点最可靠,二层、三层参考点的标准偏差远大于一层。本文设定阈值λ= 0.15 mm,经对比分析可知,型架二层及三层的点19~27超出该阈值,因此,这些参考点的可靠程度较低,不建议后续继续使用。

图8 参考点距离值的标准偏差
5 结语
从标准场参考点各分量偏差及点位偏差可以看出各参考点在不同维度的离散程度,而根据参考点距离值的标准偏差是否超过设定的阈值λ,可以进一步评估标准场参考点的可靠性。通过上述对比分析可知,型架参考点各分量及点位偏差的数据离散程度远大于地面参考点,且型架上点19~27的距离值的标准偏差超过设定的阈值0.15 mm,表明该区域的参考点不可靠,建议更换该区域参考点位置或进一步分析有无影响该区域测量结果的环境因素。

